N-fold Darboux Transformation for Integrable Couplings of AKNS Equations∗

Jing Yu(虞静),Shou-Ting Chen(陈守婷),Jing-Wei Han(韩敬伟), and Wen-Xiu Ma(马文秀)

1School of Science,Hangzhou Dianzi University,Hangzhou 310018,China

2School of Mathematics and Physical Science,Xuzhou Institute of Technology,Xuzhou 221111,China

3School of Information Engineering,Hangzhou Dianzi University,Hangzhou 310018,China

4Department of Mathematics and Statistics,University of South Florida,Tampa,FL,33620-5700,USA

5College of Mathematics and Systems Science,Shandong University of Science and Technology,Qingdao 266590,China

6International Institute for Symmetry Analysis and Mathematical Modeling,Department of Mathematical Sciences,North-West University,Ma fikeng Campus,Private Bag X2046,Mmabatho 2735,South Africa

1 Introduction

Integrable couplings of soliton equations have been attracted much attention over the last few decades.Generally speaking,for a given integrable system of evolution equations ut=K(u),a new system consisting of the original system and its linearized system

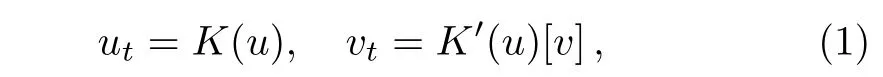
is still integrable. Here K′(u)[v]denotes the Gateaux derivative of K(u)≡K(u,Dxu,...)with respect to u in a direction v,i.e.

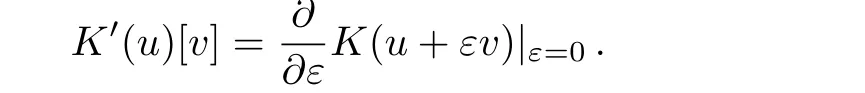
The second part vt=K′(u)[v]in the above new system(1)is a special integrable couplings of the original system ut= K(u).So far,the method for constructing integrable couplings of soliton equations mainly included perturbations,[1−2]enlarging spectral problems,[3−6]creating new loop algebras,[7−8]and multiintegrable couplings.[9−11]The study of integrable couplings of soliton equations brought two major benefits.One is to generalize the symmetry problem,[12−13]the other is to provide clues towards complete classification of integrable systems.

It is well-known that DT[14−19]is always regarded as one of the most effective method to construct solutions of integrable equations.The main procedures are listed as follows.Suppose the integrable equations are associated with the following spectral problem

which is transformed into

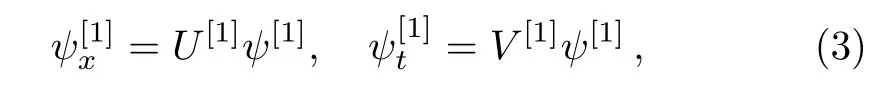
under a gauge transformation

By Refs.[19–20],we know that T in Eq.(4)must satisfy following conditions

according to Eq.(3).It is crucial for us to search for T in Eq.(4)so that U[1]and V[1]have the same forms as U and V. Repeating N times,N-fold DT can be constructed. In 2006,the authors proposed determinant representation of DT for the integrable equations.Without iterating,N-fold DT and N-transformed solutions are derived for many integrable equations,such as AKNS equation,[21]derivative nonlinear Schrödinger(DNLS)equation,[22]Gerdjikov-Ivanov(GI)equation,[23]Chen-Lee-Liu(CLL)equation,[24]and so on.[25−28]Accordingly,many important solutions of these equations are constructed in these references.For example,soliton solutions,rogue wave solutions,breather solutions,and so forth.To this day,no researchers considered determinant representations of the N-fold DT and N-transformed new solutions for the integrable couplings of soliton equations.So we will solve this question in this paper.

The paper is organized as follows.In the next section,we recall the construction of ICAKNS equations.Then in Sec.3,determinant representations of N-fold DT and N-transformed solutions are constructed for the ICAKNS equations.And in Sec.4,under the constraint condition q= −p∗and s= −r∗,we obtain ones of ICNLS equations.Some conclusions and discussions are listed in the last section.

2 Integrable Couplings of the AKNS Equations

In this section,we will briefly recall the construction of ICAKNS equations.Firstly,we know that the ICAKNS system is associated with the following the spatial spectral problem

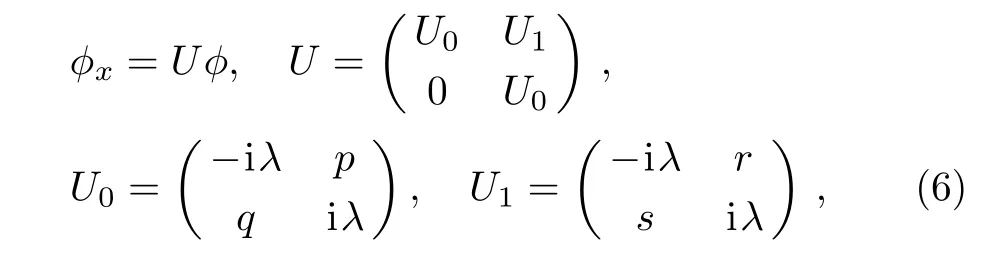
where λ is a spectral parameter,p,q,r and s are potentials, ϕ =(ϕ1,ϕ2,ϕ3,ϕ4)Tis an eigenfunction.Solving the stationary equation

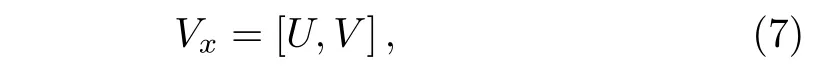
where

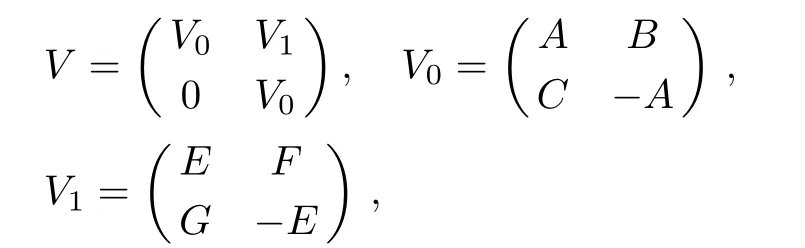
we have

Taking

and comparing the coefficients of the same power of λ,we have

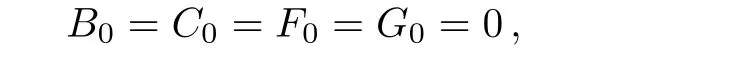
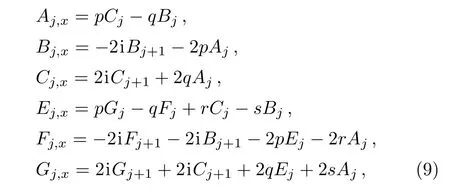
where j≥0.It is easy to find that A0,x=E0,x=0.Choosing A0=E0=−i,and taking constants of integral to be zero,we obtain all terms Aj,Bj,Cj,Ej,Fj,Gj(j≥1).The first three terms are listed as follows:

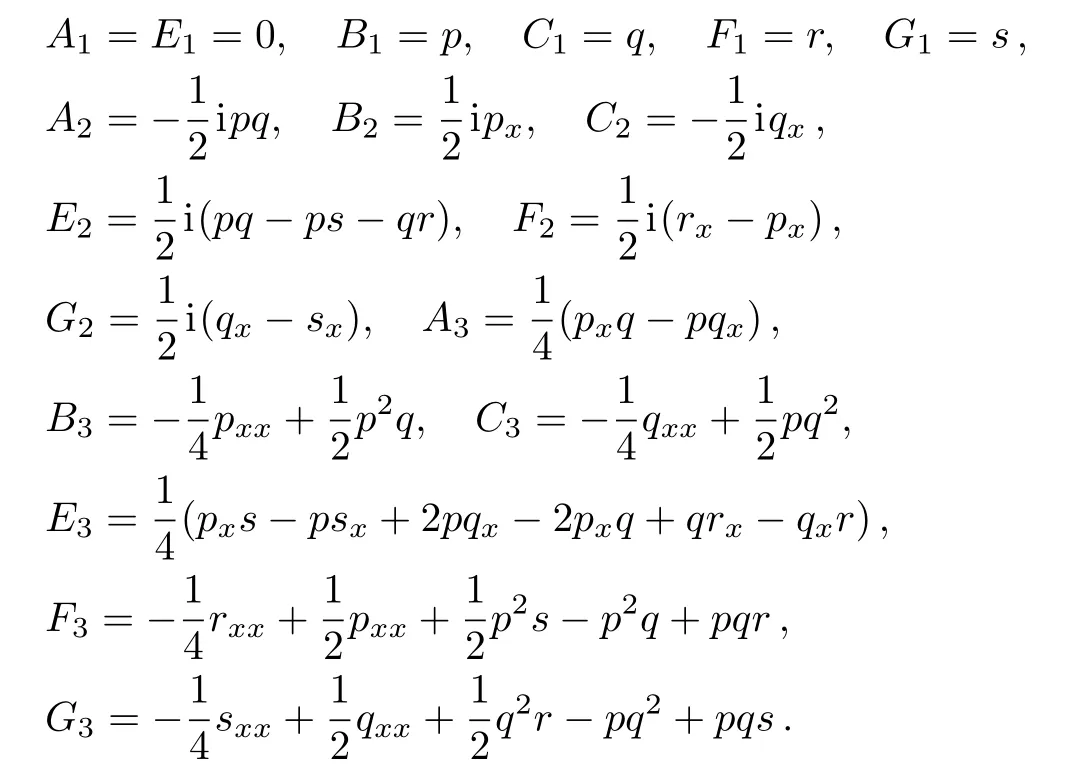
Secondly,let us introduce the temporal parts of the spectral problem(6)

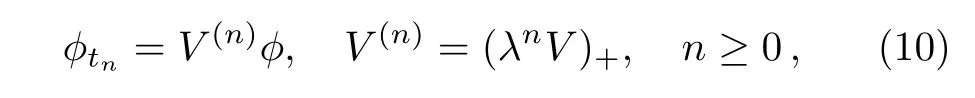
where“+”means non-negative power.The compatible condition of(6)and(10)yields to

Substituting U and V(n)into Eq.(11),we have

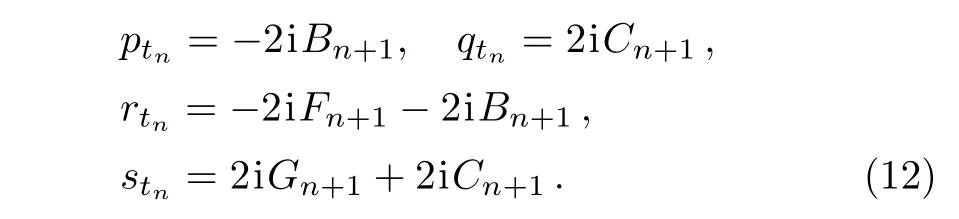
Lastly,when n=2 in Eq.(12),we obtain the ICAKNS equations

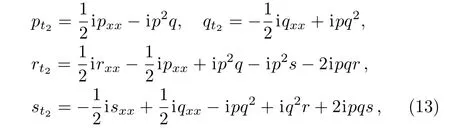
whose Lax pairs are given by U and V(2)as follows:

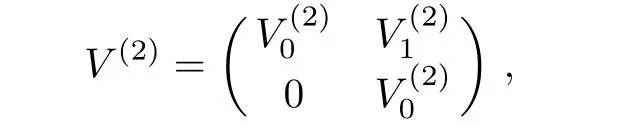
with

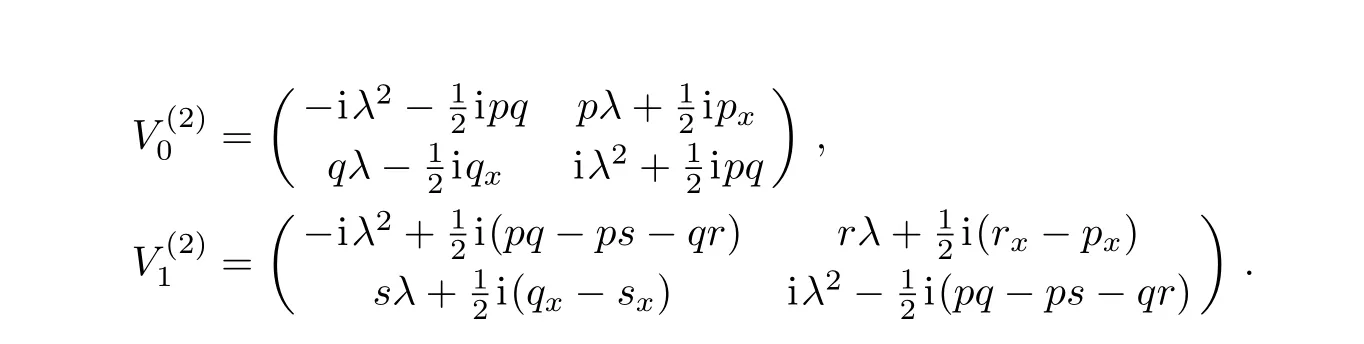
3 DT of ICAKNS Equations(13)

In this section,we will derive determinant representation of DT for the ICAKNS equations(13).To this end,we firstly suppose the Darboux matrix is

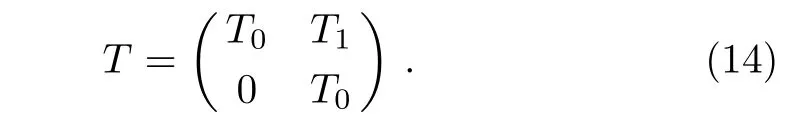
The spectral problem ϕx=Uϕ,ϕt2=V(2)ϕ is transformed into ϕ[1]x=U[1]ϕ[1], ϕ[1]t2=(V(2))[1]ϕ[1]under the DT(14).Here U[1],(V(2))[1]share the same forms as U,V(2).After a direct calculation,we have

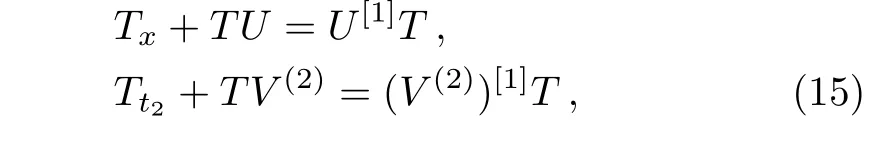
or

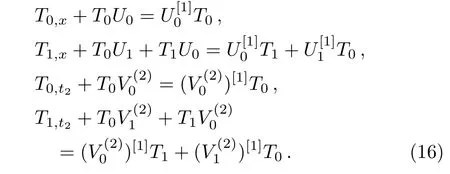
Secondly,without loss of generality of the DT,let us suppose the trial Darboux sub-matrices T0and T1are of the forms:

Here,ak,bk,ck,dk,ek,fk,gk,hk(k=0,1),which are determined later,are all functions of eigenfunctions.Substituting(17)and(18)into the spatial part of Eq.(16),and comparing the coefficients of the same power of λ,we have

Meanwhile,if we apply the similar procedure to the temporal part of Eq.(16),we have

It is easy to know that a1,d1,e1and h1are all independent of variables x and t2. So,a1,d1,e1,and h1are all constants. In order to obtain the non-trivial new solutions and without losing any generality,we choose a1=d1=e1=h1=1.Thus,the Darboux sub-matrices T0and T1are of the forms

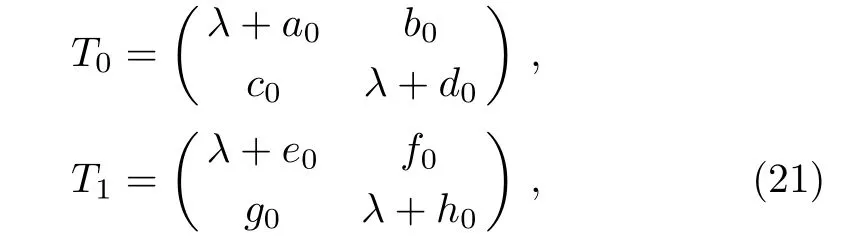
where a0,b0,c0,d0,e0,f0,g0,h0are undetermined functionsof(x,t).And thetransformed new solutions p[1],q[1],r[1],s[1]are given by

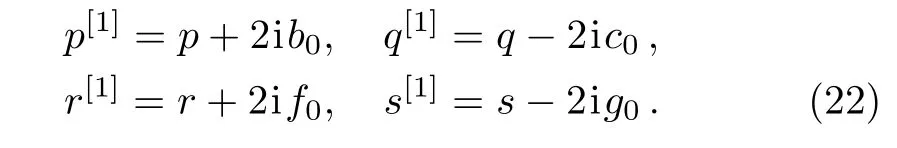
Denote that 2N eigenfunctions

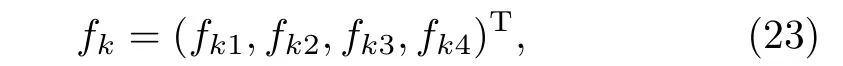
are basic solutions of systems(6)and(10)(n=2)with λ=λk(1≤k≤2N).

Theorem 1The elements of one-fold DT for the ICAKNS equations(13)are determined by the eigenfunctions f1,f2associated with the parameters λ1,λ2as

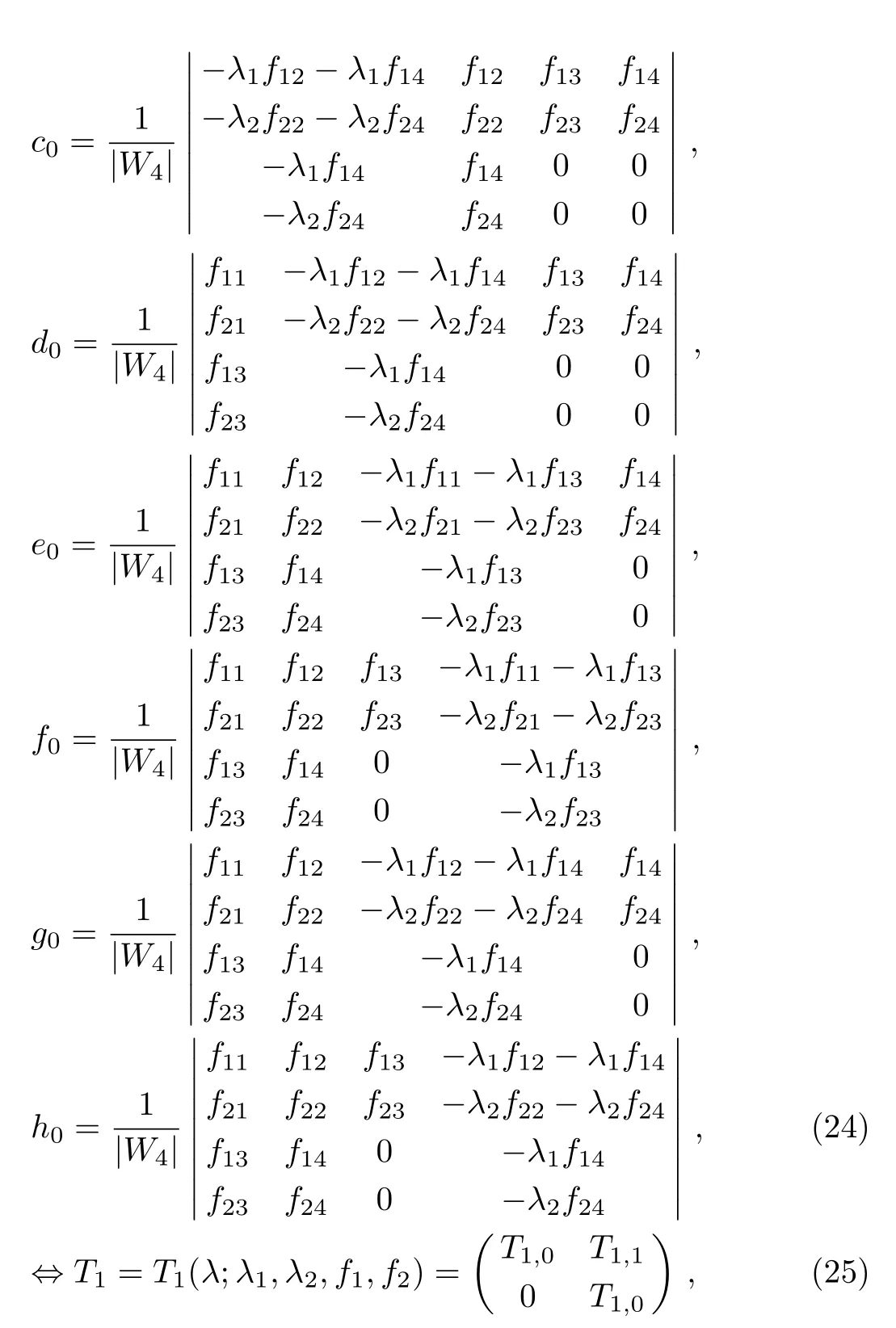
where the Darboux sub-matrices T1,0and T1,1can be written as the determinant forms:

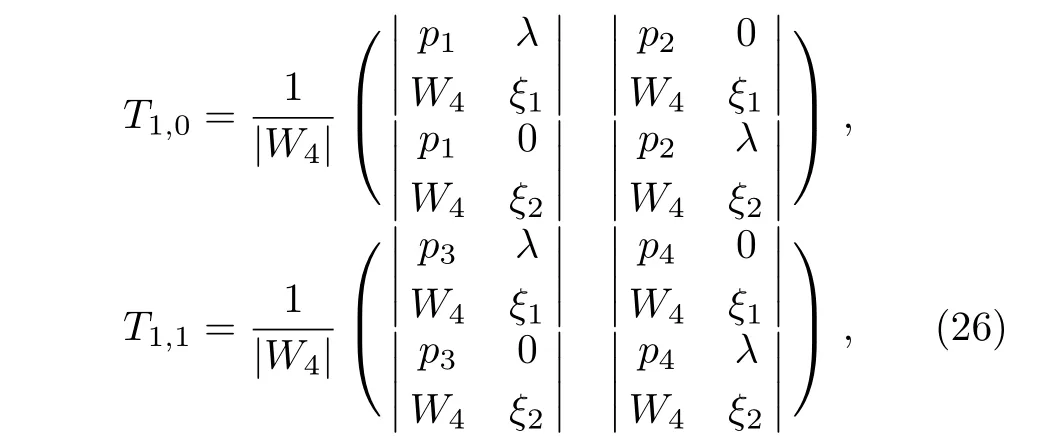
with

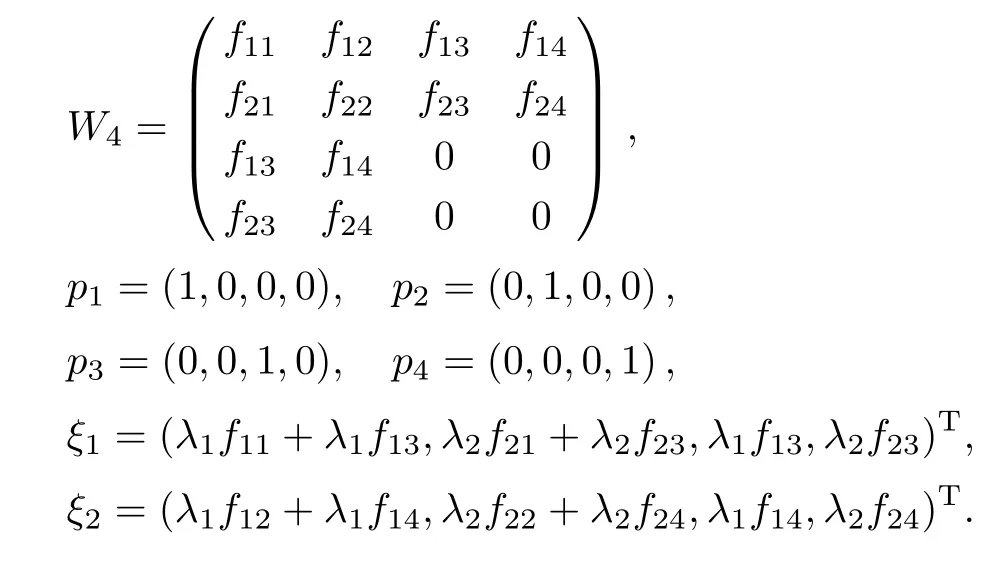
Then,the new solutions p[1],q[1],r[1],s[1]are given by

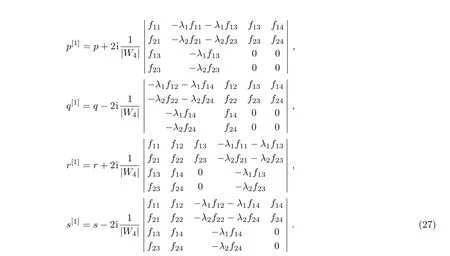
Proof 1By making use of the general fact of the DT,i.e.T1(λ;λk)|λ=λkfk=0(k=1,2),all a0,b0,c0,d0,e0,f0,g0,h0are expressed by the eigenfunctions f1,f2associated with λ1,λ2.Substituting b0,c0,f0,g0given in Eq.(24)into Eq.(22),new solutions are given as in Eq.(27).After a direct and tedious calculation,we show that T1in Eq.(25)and new solutions in Eq.(27)indeed satisfy the temporal part(20).So the ICAKNS equations(13)are covariant under the transformation T1in Eq.(25).Thus,T1in Eq.(25)is the DT of ICAKNS equations(13).

In what follows,our key task is to establish the determinant representation of the N-fold DT for the ICAKNS equations(13).To this end,we arrive at the following conclusion.

Theorem 2N-fold DT for the ICAKNS equations(13)can be expressed by

where the Darboux sub-matrices TN,0,TN,1are given by the following determinant forms:

with

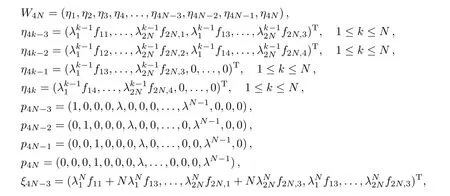
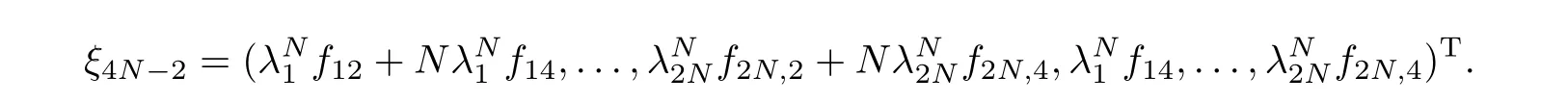
Correspondingly,N-transformed solutions of ICAKNS equations(13)become

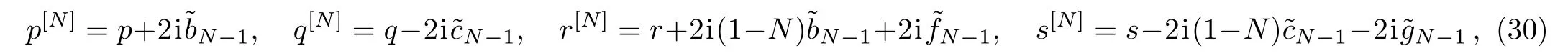
where

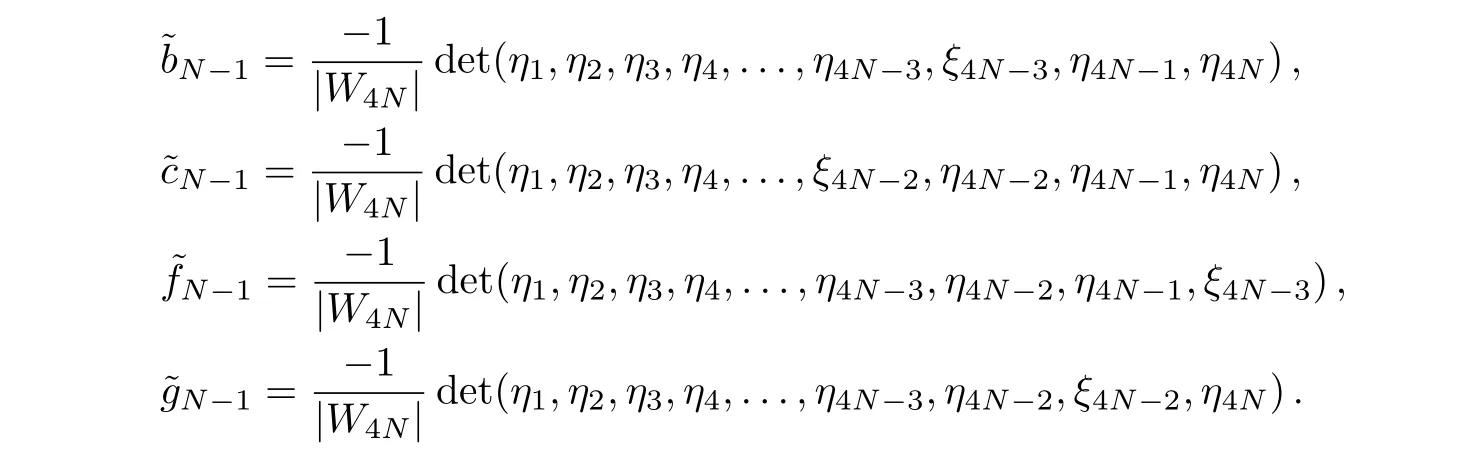
Proof 2According to the form of T1in Eq.(25),the N-fold DT should be of the form(28),where

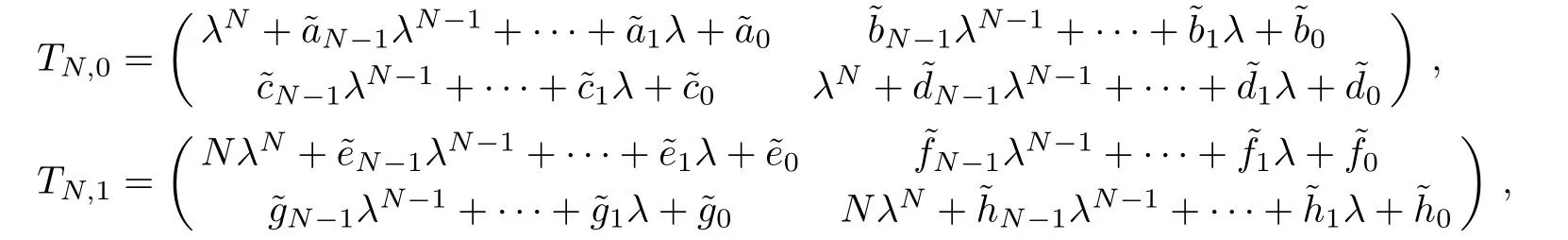
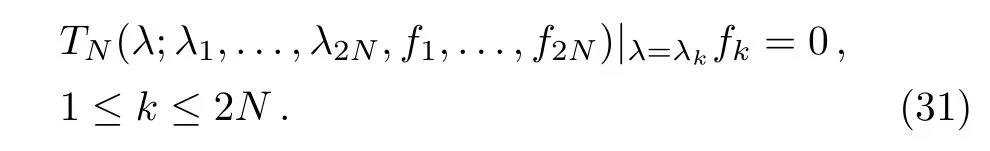
Under a covariant requirement of the spectral problem of the ICAKNS equations(13),the transformed spatial spectral problem should be

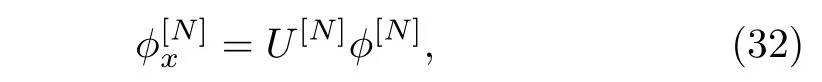
where

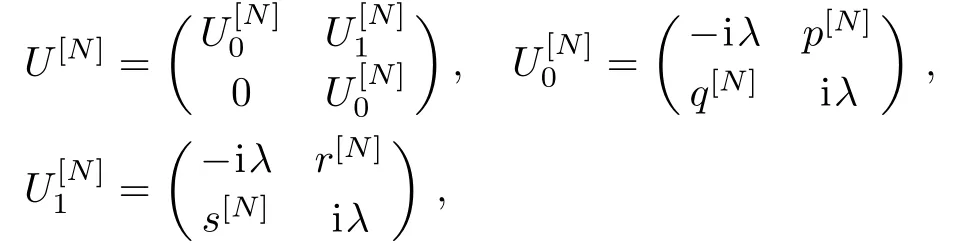
and then

Substituting TNgiven by Eq.(28)into the above equation(33),and comparing the coefficients of λN,we get the N-transformed solutions(30).As for the temporal part(t2)spectral problem of the ICAKNS equations(13),we arrive at the same conclusion after a similar discussion.

4 Solutions of Integrable Couplings of the NLS Equations

When the reduction conditions q= −p∗and s= −r∗are imposed on the ICAKNS equations(13),we have the ICNLS equations

whose Lax pairs are given by

Lemma 1If(ϕ1,ϕ2,ϕ3,ϕ4)Tis a solution of Eq.(35)with λ = λ1,thenis a solution of Eq.(35)with λ =.

By making use of Lemma 1,if we choosethen N-fold DT and N-transformed solutions of the ICNLS equations are obtained.In what follows,as a special example,we choose the seed solution p=r=0 in Eq.(35),we have

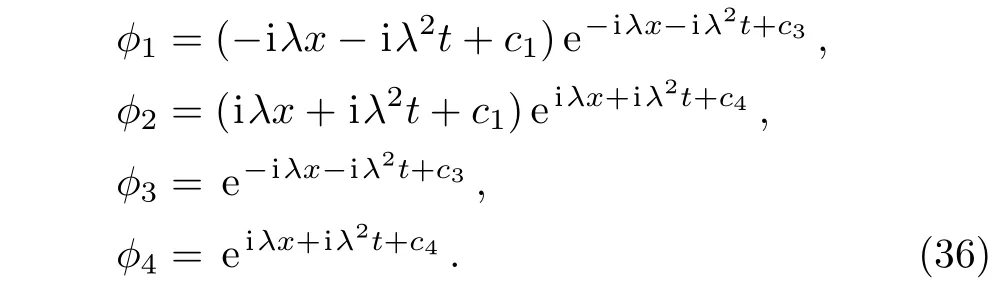
Furthermore,let c1= c2= c3= c4= 0 in Eq.(36),and then the corresponding eigenfunction f1=(f11,f12,f13,f14)Tassociated with λ1is given by

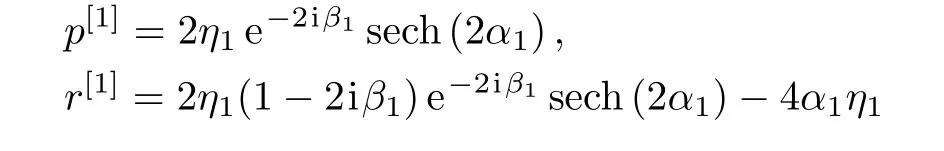
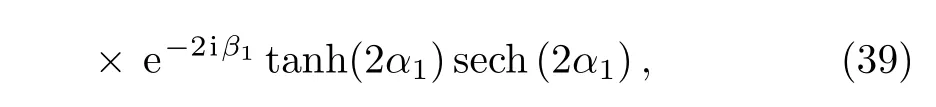
which are one-soliton solutions of the ICNLS equations(34).

5 Conclusions and Discussions

DT has been widely applied to many notable integrable equations,and several literatures can be found to study DT for integrable couplings of soliton equations,for example Refs.[29–34].After some careful comparisons,we found some differences and advantages between these references and our paper.On one hand,comparing Ref.[29]with our paper,the main difference include that the spectral problem of ICAKNS system is different.Therefore,the representation of DT,the numbers of basic solutions and the representation of new solutions are also different.On the other hand,there are some advantages of our paper when compared with Ref.[34].In our paper,the determinant representations of N-fold DT and N-transformed solutions for the ICAKNS equations(13)are constructed in Eqs.(28)and(30),respectively.While in Ref.[34],they only obtained the representations of one-fold DT and onetransformed solutions.And the other advantage of our paper is to derive the determinant representation of N-fold DT for the ICAKNS equations(13)without iterating.

Above all,in this paper,we have constructed determinant representations of N-fold DT(28)and N-times transformed solutions(30)for the ICAKNS equations(13).Imposing the constraint conditions q= −p∗,s= −r∗,we have obtained ones of the ICNLS equations(34).After choosing the initial values p=r=0,we derived soliton solutions(39)of the ICNLS equations(34).We believe that this method will be successfully applied to the other integrable couplings of soliton equations.And there maybe exist the other solutions for integrable couplings of equations.Both of these questions will be considered in our future paper.

[1]W.X.Ma,Meth.Appl.Anal.7(2000)21.

[2]W.X.Ma and B.Fuchssteiner,Phys.Lett.A 213(1996)49.

[3]W.X.Ma,Phys.Lett.A 316(2003)72.

[4]W.X.Ma,J.Math.Phys.46(2005)033507.

[5]W.X.Ma,X.X.Xu,and Y.F.Zhang,Phys.Lett.A 351(2006)125.

[6]W.X.Ma,X.X.Xu,and Y.F.Zhang,J.Math.Phys.47(2006)053501.

[7]F.K.Guo and Y.F.Zhang,J.Math.Phys.44(2003)5793.

[8]Y.F.Zhang,Chaos,Solitons&Fractals 21(2004)305.

[9]W.X.Ma,J.H.Meng,and H.Q.Zhang,Int.J.Nonlinear Sci.Numer.Simul.14(2013)377.

[10]S.M.Yu,Y.Q.Yao,S.F.Shen,and W.X.Ma,Commun.Nonlinear Sci.Numer.Simular.23(2015)366.

[11]W.X.Ma,J.H.Meng,and M.S.Zhang,Math.Comput.Simulat.127(2016)166.

[12]W.X.Ma and B.Fuchssteiner,Chaos,Solitons&Fractals 7(1996)1227.

[13]W.X.Ma,J.Math.Phys.43(2002)1408.

[14]D.Levi,O.Ragnisco,and A.Sym,Lett.Nuovo Cimento 33(1982)401.

[15]D.Levi,O.Ragnisco,and A.Sym,IL Nuovo Cimento 83B(1984)34.

[16]G.Neugerauer and R.Meinel,Phys.Lett.100A(1984)467.

[17]Y.S.Li,X.S.Gu,and M.R.Zou,Acta Math.Sin.3(1987)143.

[18]C.H.Gu and Z.X.Zhou,Lett.Math.Phys.13(1987)179.

[19]V.B.Mateev and M.A.Salle,Darboux Transformations and Solitons,Springer-Verlag,Berlin(1991).

[20]C.H.Gu,H.S.Hu,and Z.X.Zhou,Darboux Transformations in Integrable System,Springer,Dortrecht(2006).

[21]J.S.He,L.Zhang,Y.Cheng,and Y.S.Li,Sci.China Math.49A(2006)1867.

[22]S.W.Xu,J.S.He,and L.H.Wang,J.Phys.A:Math.Theor.44(2011)305203.

[23]S.W.Xu and J.S.He,J.Math.Phys.53(2012)063507.

[24]Y.S.Zhang,L.J.Guo,J.S.He,and Z.X.Zhou,Lett.Math.Phys.105(2015)853.

[25]S.B.Shan,C.Z.Li,and J.S.He,Commun.Nonlinear Sci.Numer.Simulat.18(2013)3337.

[26]J.W.Ha,J.Yu,and J.S.He,Mod.Phys.Lett.B 27(2013)1350216.

[27]J.Yu,J.W.Han,and J.S.He,Z.Naturforsch A 70(2015)1039.

[28]C.C.Zhang,C.Z.Li,and J.S.He,Math.Meth.Appl.Sci.38(2015)2411.

[29]Q.L Zha,J.Inner Mongolia Nor.Univ.(Nature Science Edition)41(2012)109.

[30]X.X.Xu,Appl.Comput.Math.3(2014)240.

[31]X.X.Xu,Commun.Nonlinear.Sci.Numer.Simulat.23(2015)192.

[32]Q.L.Zha,J.Inner Mongolia Nor.Univ.45(2016)598.

[33]F.J.Yu and S.Feng,Math.Meth.Appl.Sci.40(2017)5515.

[34]W.X.Ma and Y.J.Zhang,Rev.Math.Phys.30(2018)1850003.