On Non-Abelian Extensions of 3-Lie Algebras∗

Li-Na Song(宋丽娜),Abdenacer Makhlouf, and Rong Tang(唐荣)

1Department of Mathematics,Jilin University,Changchun 130012,China

2University of Haute Alsace,Laboratoire de Math´ematiques,Informatique et Applications,Mulhouse,France

1 Introduction

Ternary Lie algebras(3-Lie algebras)or more generally n-ary Lie algebras are a natural generalization of Lie algebras.They were introduced and studied first by Filippov in Ref.[1].This type of algebras appeared also in the algebraic formulation of Nambu Mechanics,[2]generalizing Hamiltonian mechanics by considering two hamiltonians,see Ref.[3]and also Ref.[4].Ternary brackets were also considered,in contexts of String Theory and M-Theory,by Basu and Harvey for lifted Nahm equations,[5]and by Bagger and Lambert in a construction of an N=2 supersymmetric version of the worldvolume theory.[6]For more applications,see also Refs.[7–11].

Several algebraic aspects of n-Lie algebras were studied in the last years.The concept of Lie algebra representation was extended naturally to 3-Lie algebras first in Ref.[12].In this framework,adjoint representations of a 3-Lie algebra(g,[·,·,·]g)are maps Lx,y:g → g defined by Lx,y(z)=[x,y,z]g,where x,y are fixed elements.Moreover the set∧2g,of so called fundamental objects,is endowed with a structure of Leibniz algebra.[13]A cohomology is also defined in Refs.[14–16].Bai and her collaborators studied realizations and classifications of n-Lie algebras.[17−18]It turns out that a structure of graded Lie algebra is defined on the cochain complex,see Ref.[19].For more details about 3-Lie algebras developments,see review articles.[20−21]

In Ref.[22],the authors introduced the notion of a generalized representation of a 3-Lie algebra,by which abelian extensions of 3-Lie algebras are studied.Due to its difficulty and less of tools,non-abelian extensions of 3-Lie algebras are not studied.In this paper,motivated by works in Refs.[22–23],we find a suitable approach which uses Maurer-Cartan elements to study non-abelian extensions of 3-Lie algebras.We also show that the Leibniz algebra on the space of fundamental objects is a non-abelian extension of Leibniz algebras.

The paper is organized as follows.In Sec.2,we provide a summary of non-abelian extensions of Leibniz algebras and cohomologies of 3-Lie algebras.A characterization of non-abelian extensions of a 3-Lie algebra by another 3-Lie algebra is given in Sec.3 and several examples provided.In Sec.4,we show that there is a one-to-one correspondence between isomorphism classes of non-abelian extensions of 3-Lie algebras and equivalence classes of Maurer-Cartan elements.Finally,we analyze in Sec.5 the corresponding Leibniz algebra structure on the space of fundamental objects and show that it is a non-abelian extension of Leibniz algebras.

2 Preliminaries

Let K be an algebraically closed field of characteristic 0 and all the vector spaces in this paper considered over K.

2.1 Non-Abelian Extensions of Leibniz Algebras

A Leibniz algebra is a vector space k endowed with a linear map[·,·]k:k⊗ k → k satisfying

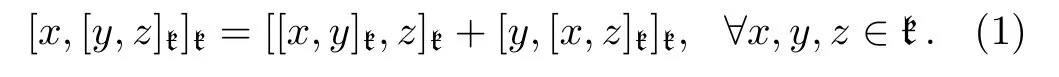
This is in fact a left Leibniz algebra.In this paper,we only consider left Leibniz algebras which we call Leibniz algebras.

Let(k,[·,·]k)be a Leibniz algebra. We denote by DerL(k)and DerR(k)the set of left derivations and the set of right derivations of g respectively:

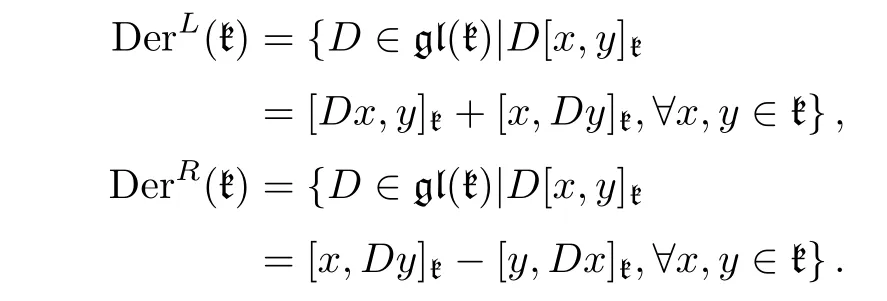
Note that the right derivations are called anti-derivations in Refs.[24–25]. It is easy to see that for all x ∈ k,:k−→ k,which is given byis a left derivation;:k−→ k,which is given by(y)=[y,x]k,is a right derivation.

Definition 1

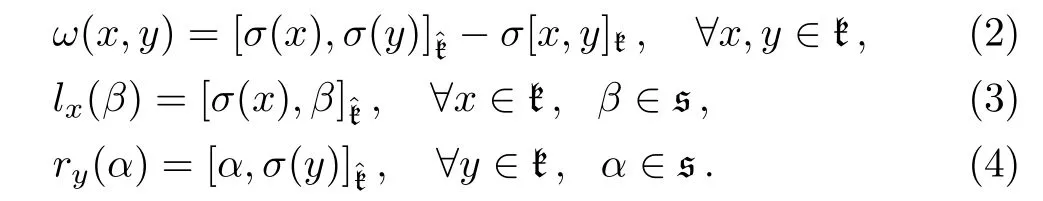
Given a linear section,we havek ⊕ s as vector spaces,and the Leibniz algebra structure oncan be transferred to k⊕s:

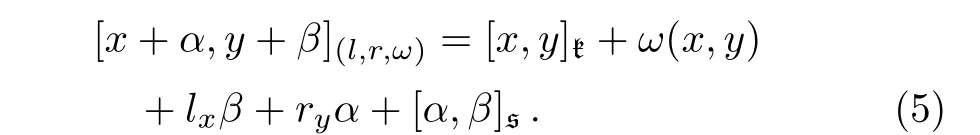
Proposition 1Withtheabovenotations,(k⊕s,[·,·](l,r,ω))is a Leibniz algebra if and only if l,r,ω satisfy the following equalities:

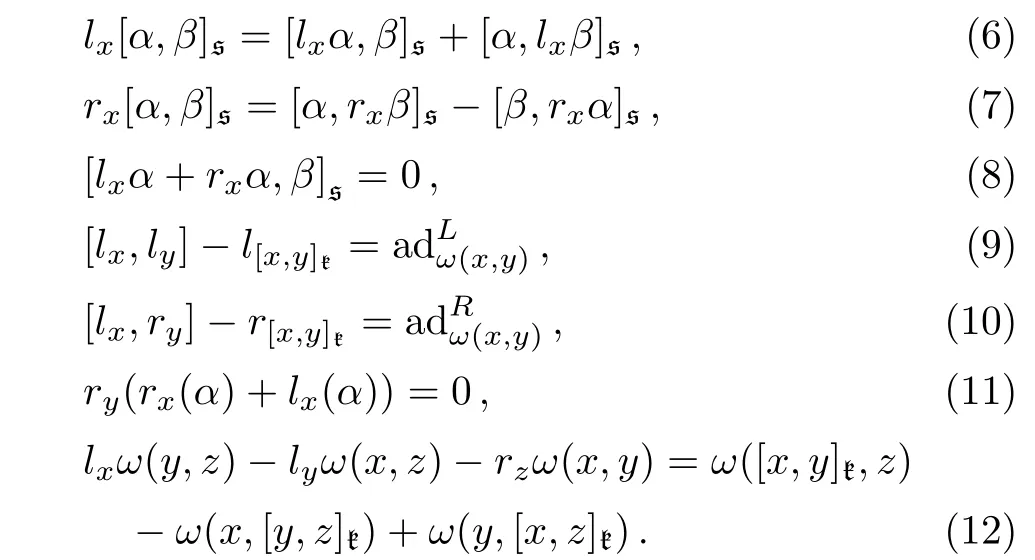
Equation(6)means that lx∈DerL(s)and Eq.(7)means that rx∈DerR(s).See Ref.[26]for more details about non-abelian extensions of Leibniz algebras.

2.2 3-Lie Algebras and Their Representations

We recall in this section definitions,representations and cohomology of 3-Lie algebras.

Definition 2A 3-Lie algebra is given by a vector space g together with a skew-symmetric linear map[·,·,·]g:∧3g→g such that the following identity holds:

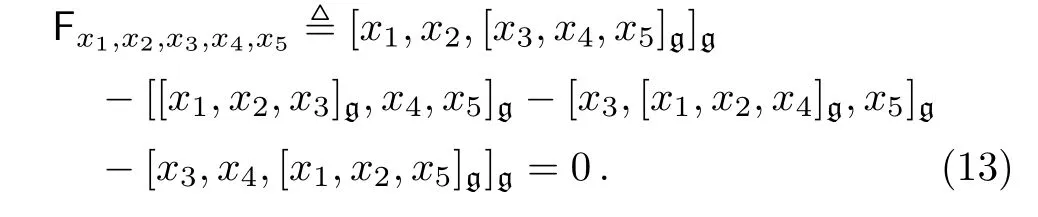
The identity(13)is called Fundamental Identity(FI)or sometimes Nambu identity.

Definition 3A morphism of 3-Lie algebras f :(g,[·,·,·]g) → (h,[·,·,·]h)is a linear map f:g → h such that

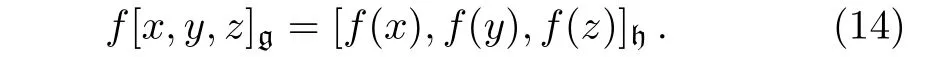
We call elements in∧2g fundamental objects of the 3-Lie algebra(g,[·,·,·]g).One defines a bilinear operation[·,·]Fon ∧2g,given by

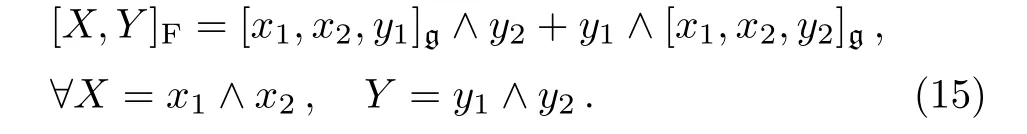
It turns out that(∧2g,[·,·]F)is a Leibniz algebra,[13]and it plays an important role in the theory of 3-Lie algebras.

The concept of representation introduced by Kasymov is defined as follows.

Definition 4(Ref.[12])A representation ρ of a 3-Lie algebra g on a vector space V is given by a linear map ρ:∧2g−→ gl(V),such that for all x1,x2,x3,x4∈ g,there holds:

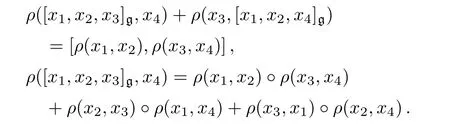
It leads to the following semidirect product for 3-Lie algebras.

Lemma 1Let g be a 3-Lie algebra,V a vector space and ρ :∧2g → gl(V)a skew-symmetric linear map.Then(V;ρ)is a representation of g if and only if there is a 3-Lie algebra structure on the direct sum of vector spaces g⊕V,defined by

for xi∈g,vi∈V,1≤i≤3.

The previous 3-Lie algebra structure is called semidirect product and denoted by g nρV.

Furthermore,there is a cohomology of 3-Lie algebras with coefficients in a representation(V;ρ).First pcochains on g are defined to be linear maps

Denote the space of p-cochains by Cp(g,V).Then the coboundary operator δ:Cp−1(g,V) −→ Cp(g,V)is defined as

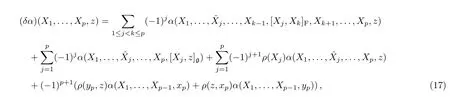
here Xi=xi∧yifor i=1,...,p and z∈g.

3 Non-Abelian Extensions of3-Lie Algebras

We discuss in this section non-abelian extensions of 3-Lie algebras.First we recall some basics.

Definition 5A non-abelian extension of a 3-Lie algebra(g,[·,·,·]g)by a 3-Lie algebra(h,[·,·,·]h)is a short exact sequence of 3-Lie algebra morphisms:is a 3-Lie algebra.

A section of a non-abelian extensionof g by h is a linear map s:g −→such that p ◦s=id.

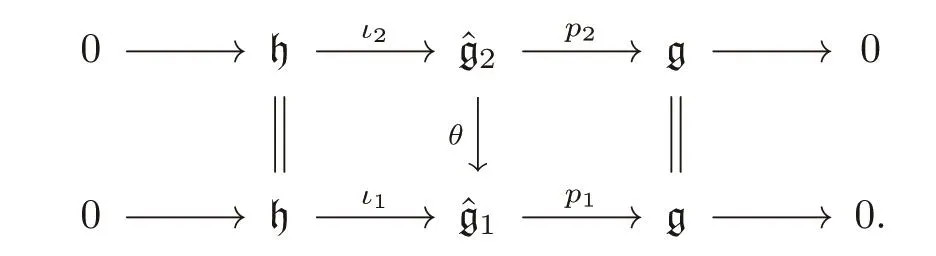
Definition 6Two extensions of g by h,(,[·,·,·]ˆg1)and(,[·,·,·]ˆg2),are said to be isomorphic if there exists a 3-Lie algebra morphism θ:such that we have the following commutative diagram:

Given a section s of a non-abelian extensionof g by h,we can define ρ :∧2g−→ gl(h),ν :g−→ Hom(∧2h,h)and ω :∧3g −→ h respectively by

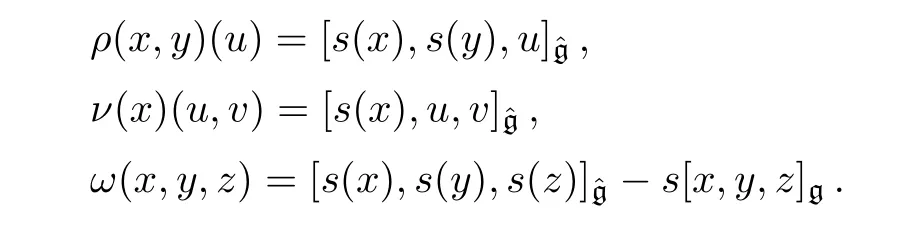
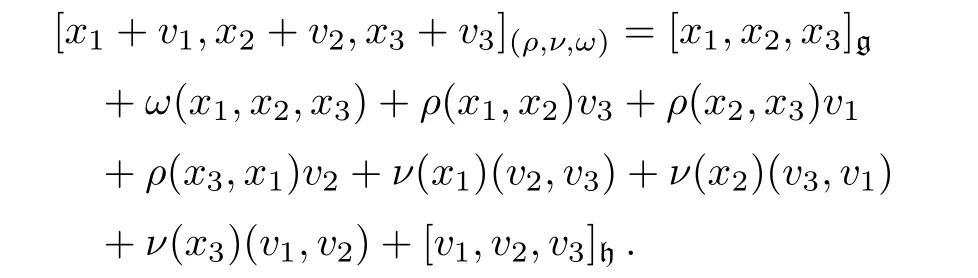
The following proposition provides the conditions on ρ,ν and ω such that(g⊕h,[·,·,·](ρ,ν,ω))is a 3-Lie algebra.

Proposition 2The pair(g ⊕ h,[·,·,·](ρ,ν,ω)),defined above,is a 3-Lie algebra if and only if ρ,ν and ω satisfy,for all x1,...,x5∈g,v1,...,v5∈h,the following conditions

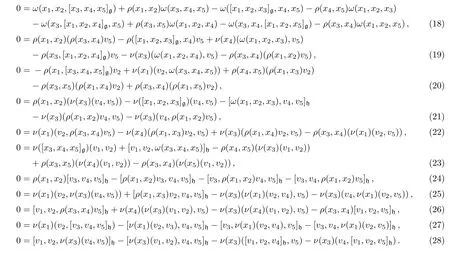
ProofThe proof is obtained by straightforward computations of the fundamental identity for different combinations of elements and the converse is direct.

Example 1We consider g to be the simple 4-dimensional 3-Lie algebra defined with respect to a basis{x1,x2,x3,x4}by the skew-symmetric brackets

and h to be the 3-dimensional 3-Lie algebra defined with respect to basis{v1,v2,v3}by

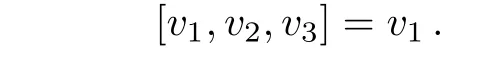
Then every non-abelian extension of g by h is given by ρ =0.The following families of ν and ω provide non-abelian extensions of g by h

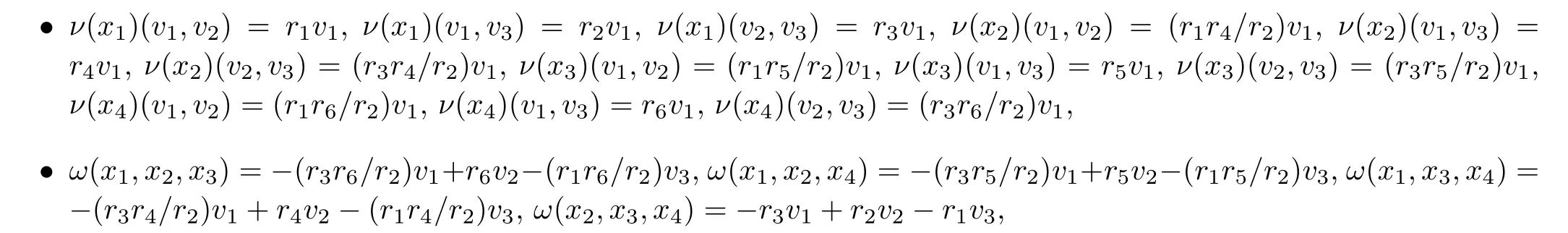
where riare parameters in K.

Example 2We consider g to be the 3-dimensional 3-Lie algebra defined with respect to a basis{x1,x2,x3}by the skew-symmetric bracket[x1,x2,x3]=x1and h to be the same 3-Lie algebra which we write with respect to basis{v1,v2,v3},that is[v1,v2,v3]=v1.Then every non-abelian extension of g by h is given by one of the following triples(ρ,ν,ω).

where riare parameters in K.

Any non-abelian extension,by choosing a section,is isomorphic to(g ⊕ h,[·,·](ρ,ν,ω)).Therefore,we only consider in the sequel non-abelian extensions of the form(g ⊕ h,[·,·](ρ,ν,ω)).

Propostion 3Let(g ⊕ h,[·,·,·](ρ1,ν1,ω1))and(g ⊕h,[·,·,·](ρ2,ν2,ω2))be two non-abelian extensions of g by h.Then the two extensions are isomorphic if and only if there is a linear map ξ:g → h such that the following equalities hold:

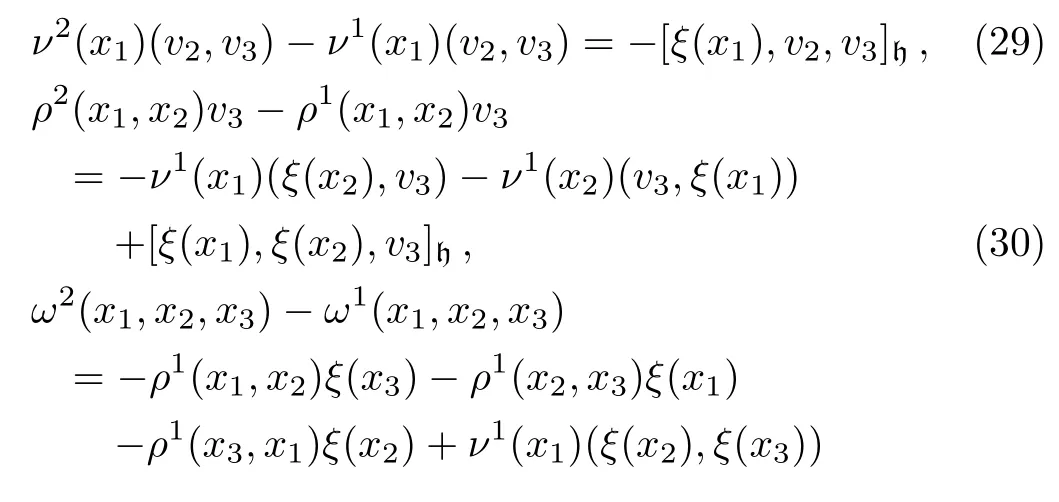
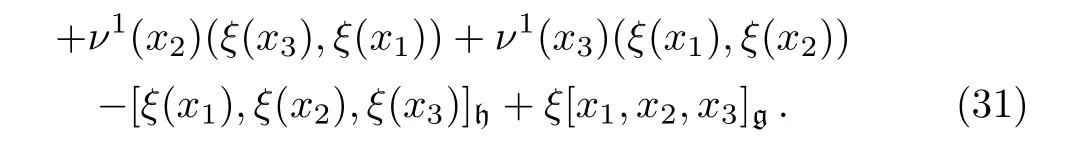
ProofLet(g⊕h,[·,·,·](ρ1,ν1,ω1))and(g⊕h,[·,·,·](ρ2,ν2,ω2))be two non-abelian extensions of g by h.Assume that the two extensions are isomorphic.Then there is a 3-Lie algebra morphism θ:g⊕h→ g⊕h,such that we have the following commutative diagram:

where ι is the inclusion and pr is the projection.Since for all x ∈ g,pr(θ(x))=x,we can assume that θ(x+u)=x−ξ(x)+u for some linear map ξ:g→ h.By

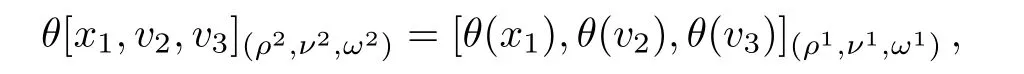
we can deduce that Eq.(29)holds.By

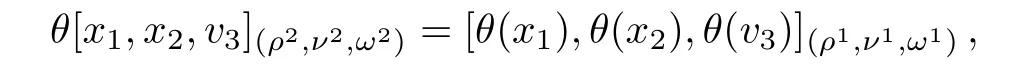
we can deduce that Eq.(30)holds.By

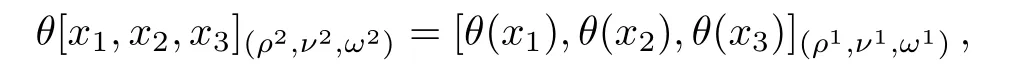
we can deduce that Eq.(31)holds.

4 Non-Abelian Extensions in Terms of Maurer Cartan Elements

In Ref.[19],the author constructed a graded Lie algebra for n-Leibniz algebras.Here,we give the precise formulas for the 3-Lie algebra case.

We define Cp(g,g)=Hom(∧2g⊗(p)···⊗ ∧2g∧ g,g)and C∗(g,g)= ⊕pCp(g,g). Let α ∈ Cp(g,g),β ∈Cq(g,g),p,q≥ 0. Let Xi=xi∧yi∈ ∧2g for i=1,2,...,p+q and xi,yi∈ g.A permutation σ ∈ Snis called an(i,n − i)-unshuffle if σ(1)< ···< σ(i)and σ(i+1)< ···< σ(n). If i=0 or n,we assume σ=id.The set of all(i,n−i)-unshuffles will be denoted by unsh(i,n−i).

Theorem 1(Ref.[19])The graded vector space C∗(g,g)equipped with the graded commutator bracket

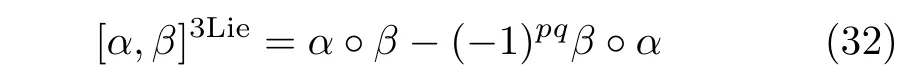
is a graded Lie algebra where α ◦ β ∈ Cp+q(g,g)is defined by

Furthermore,(C∗(g,g),[·,·]3Lie,¯δ)is a DGLA,where¯δ is given by¯δP=(−1)pδP for all P∈Cp(g,g),and δ is the coboundary operator of g with coefficients in the adjoint representation.See Ref.[22]for more details.

Remark 1The coboundary operator δ associated to the adjoint representation of the 3-Lie algebra g can be written as δP=(−1)p[µg,P]3Lie,for all P ∈ Cp(g,g),whereµg∈ C1(g,g)is the 3-Lie algebra structure on g,i.e.µg(x,y,z)=[x,y,z]g.Thus,we have¯δP=[µg,P]3Lie.

Now, we describe non-abelian extensionsusing Maurer-Cartan elements.Let(L,[·,·],d)be a differential graded Lie algebra,with L0abelian.‡The set MC(L)ofMaurer-Cartan elements of the DGLA(L,[·,·],d)is defined by

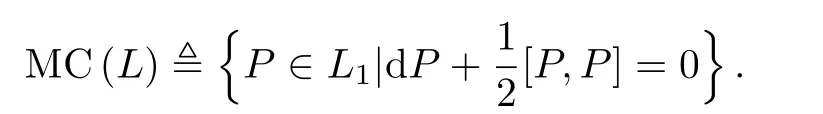
Moreover,P0,P1∈MC(L)are called gauge equivalent if and only if there exists an element ξ∈L0such that

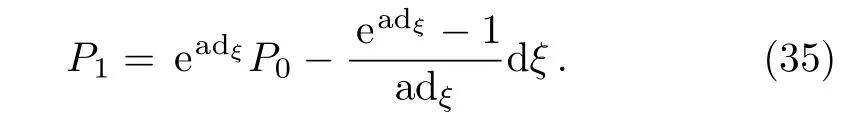
We can define a path between P0and P1.Let

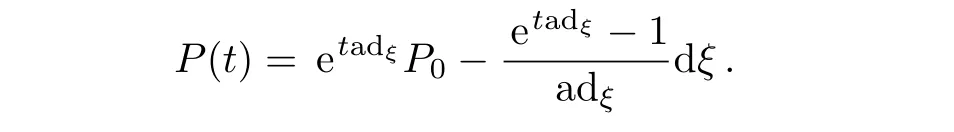
Then P(t)is a power series of t in MC(L).We have P(0)=P0and P(1)=P1.The set of the gauge equivalence classes of MC(L)is denoted by MC(L).

Let(g,[·,·,·]g)and(h,[·,·,·]h)be two 3-Lie algebras.Let g⊕h be the 3-Lie algebra direct sum of g and h,where the bracket is defined by

Lemma 2With the above notations,we haveh,h))⊂(g⊕h,h),and(C>(g⊕h,h),[·,·]3Lie,δ¯)is a sub-DGLA ofFurthermore,its degree 0 part(g⊕h,h)=Hom(g,h)is abelian.

‡This condition guarantees that the right hand side of Eq.(35)makes sense.In general,we should assume that L is equipped with a descending filtration:

which is compatible with the Lie bracket,and such that L is complete with respect to this filtration,i.e.

See Refs.[23,27]for more details.

ProofBy the definition of the bracket[·,·]3Lieandwe obtain thatis a sub-DGLA ofForwe can regard it as α ∈ Cp(g ⊕ h,h)such that α|Cp(h,h)=0.Moreover,forwe haveThus,we obtain(C(g ⊕is a sub-DGLA ofTherefore,is a sub-DGLA ofObviously,Hom(g,h)is abelian.

Proposition 4The following two statements are equivalent:

ProofBy Proposition 2,(g ⊕ h,[·,·,·](ρ,ν,ω))is a 3-Lie algebra if and only if Eqs.(18)–(28)hold.

If c=ρ+ν+ω is a Maurer-Cartan element,we have

By straightforward computations,we have

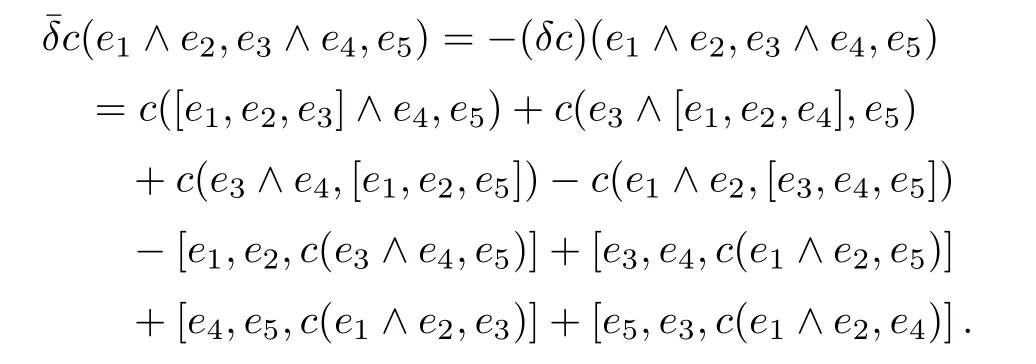
Recall the definition of the bracket[·,·,·]and the c,we have

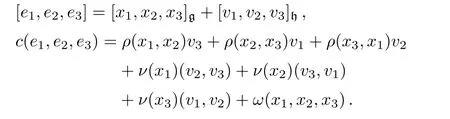
Moreover,we have

Furthermore,by the definition of the bracket in Theorem 1,we have

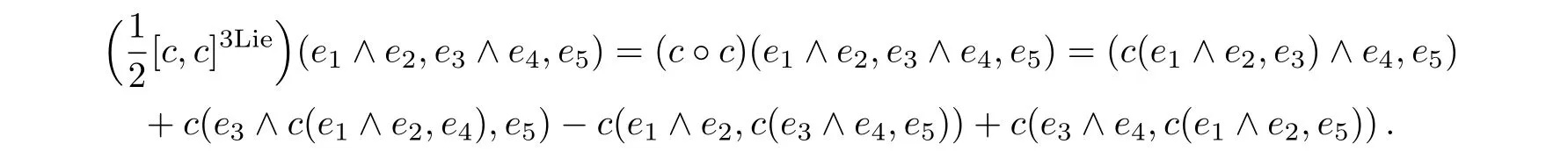
Moreover,we have

Thus,c= ρ+ν+ω is a Maurer-Cartan element if and only if Eqs.(18)–(28)hold.

Corollary 1Let g and h be two 3-Lie algebras.Then there is a one-to-one correspondence between non-abelian extensions of the 3-Lie algebra g by h and Maurer-Cartan elements in the DGLA

Theorem 2Let g and h be two 3-Lie algebras.Then the isomorphism classes of non-abelian extensions g by h oneto-one correspond to the gauge equivalence classes of Maurer-Cartan elements in the DGLA

ProofTwo elements c= ρ+ ν+ ω and c′= ρ′+ ν′+ω′in MC(L)are equivalent if there exists ξ∈ Hom(g,h)such thatMore precisely,for all ei=xi+vi∈g⊕h,we have

Furthermore,by the bracket in Theorem 1,we have

Thus,we have

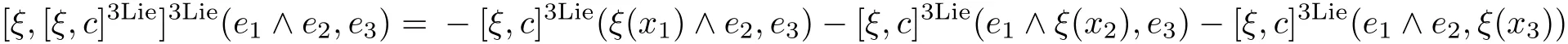
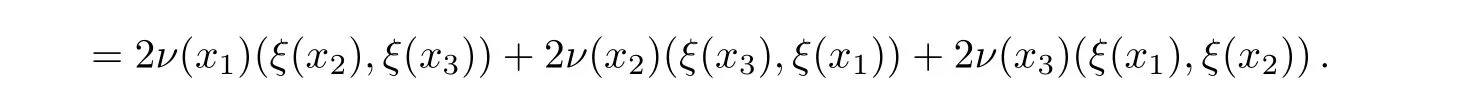
Moreover,we have

More generally,for n≥3

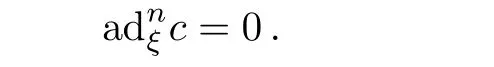
For all ei=xi+vi∈g⊕h,we have

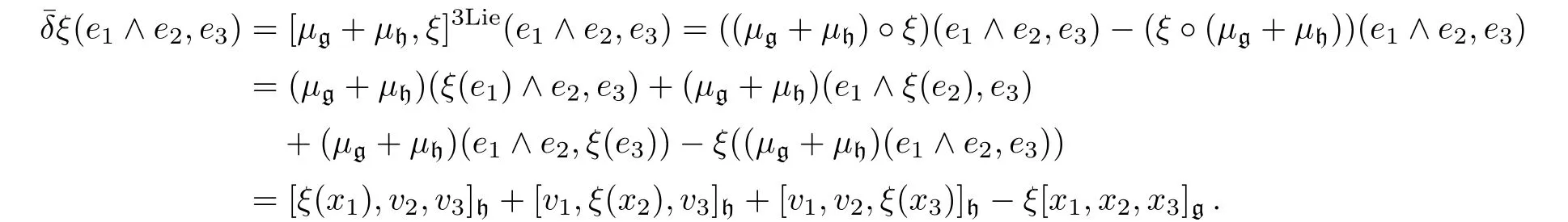
Thus,we have

Moreover,we have

More generally,for n≥3

Therefore,we have

Thus,two elements c= ρ+ν+ω and c′= ρ′+ν′+ω′in MC(L)are equivalent if and only Eqs.(29)–(31)hold.

5 Non-Abelian Extensions of Leibniz Algebras

In this section,we always assume that(g ⊕ h,[·,·](ρ,ν,ω))is a non-abelian extension of the 3-Lie algebra g by h.We aim to analyze the corresponding Leibniz algebra structure on the space of fundamental objects.Note that∧2(g⊕h)((∧2h)⊕(g⊗h))⊕(∧2g)naturally.We useto denote the Leibniz bracket on the space of fundamental objects of the 3-Lie algebra(g ⊕ h,[·,·](ρ,ν,ω)).

First we introduce a Leibniz algebra structure on(∧2h)⊕ (g ⊗ h).Define a linear map{·,·}:((∧2h)⊕ (g ⊗ h))⊗((∧2h)⊕ (g⊗h))→ (∧2h)⊕(g⊗ h)by

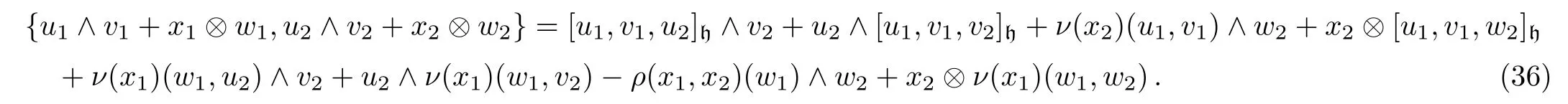
Proposition 5With the above notations,((∧2h)⊕ (g ⊗ h),{·,·})is a Leibniz algebra.

ProofBy direct computation,we have

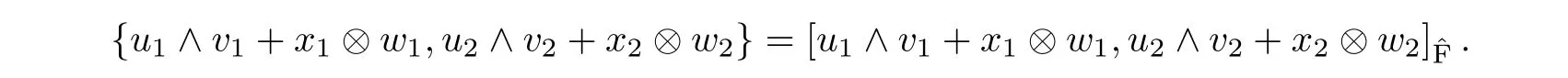
Thus,((∧2h)⊕(g⊗h),{·,·})is a Leibniz subalgebra of the Leibniz algebra

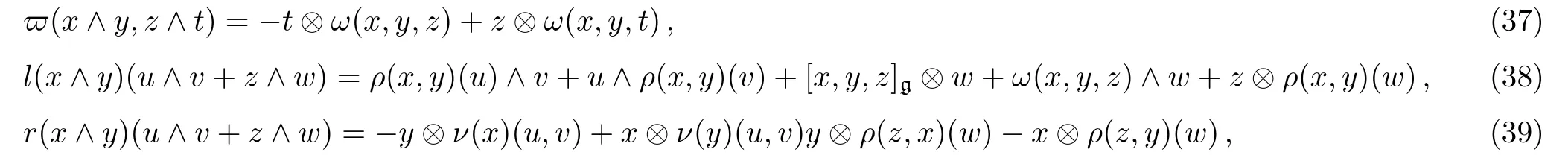
for all x,y,z,t∈g,u,v,w∈h.

Now we are ready to give the main result of this section.

Theorem 3Let(g,[·,·,·]g)and(h,[·,·,·]h)be two 3-Lie algebras and(g ⊕ h,[·,·](ρ,ν,ω))a non-abelian extension of the 3-Lie algebra g by h.Then the Leibniz algebra(∧2(g⊕h),[·,·]ˆF)is a non-abelian extension of the Leibniz algebra(∧2g,[·,·]F)by the Leibniz algebra((∧2h)⊕ (g ⊗ h),{·,·}).

ProofOne can show that conditions(6)–(12)in Proposition 1 hold directly.Thus,(∧2(g⊕h),[·,·]ˆF)is a non-abelian extension of the Leibniz algebra(∧2g,[·,·]F)by the Leibniz algebra((∧2h) ⊕ (g ⊗ h),{·,·}).Here we use a different approach to prove this theorem.Using the isomorphism between ∧2(g⊕h)and((∧2h)⊕(g⊗h))⊕(∧2g),the Leibniz algebra structure on∧2(g⊕h)is given by

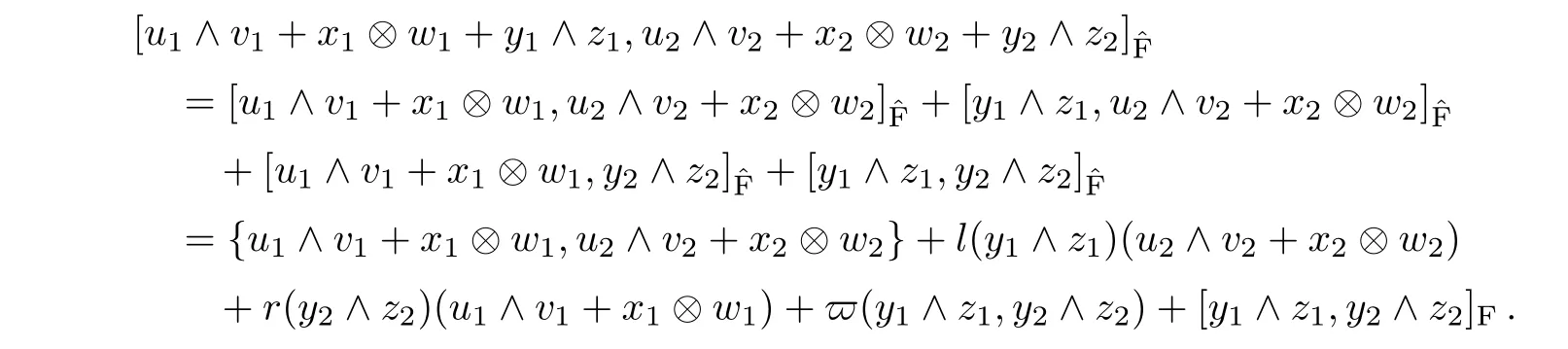
Thus,by Eq.(5),we deduce that(∧2(g⊕h),[·,·]ˆF)is a non-abelian extension of the Leibniz algebra(∧2g,[·,·]F)by the Leibniz algebra((∧2h)⊕ (g ⊗ h),{·,·}).

[1]V.T.Filippov,Sib.Mat.Zh.26(1985)126.

[2]Y.Nambu,Phys.Rev.D 7(1973)2405.

[3]L.Takhtajan,Commun.Math.Phys.160(1994)295.

[4]P.Gautheron,Lett.Math.Phys.37(1996)103.

[5]A.Basu and J.A.Harvey,Nucl.Phys.B 713(2005)136.

[6]J.Bagger and N.Lambert,Phys.Rev.D 77(2008)065008.

[7]J.Bagger and N.Lambert,Phys.Rev.D 79(2009)025002.

[8]J.Gomis,D.Rodrıguez-G´omez,M.Van Raamsdonk,and H.Verlinde,J.High Energy Phys.8(2008)094.

[9]P.M.Ho and Y.Matsuo,J.High Energy Phys.06(2008)105.

[10]P.M.Ho,R.Hou,and Y.Matsuo,J.High Energy Phys.6(2008)020.

[11]G.Papadopoulos,J.High Energy Phys.5(2008)054.

[12]Sh.M.Kasymov,Algebra i Logika 26(1987)277.

[13]Y.Daletskii and L.Takhtajan,Lett.Math.Phys.39(1997)127.

[14]J.Figueroa-O’Farrill,J.Math.Phys.50(2009)113514.

[15]J.A.de Azc´arraga and J.M.Izquierdo,J.Phys.Conf.Ser.175(2009)012001.

[16]L.Takhtajan,St.Petersburg Math.J.6(1995)429.

[17]R.Bai,C.Bai,and J.Wang,J.Math.Phys.51(2010)063505.

[18]R.Bai,G.Song,and Y.Zhang,Front.Math.China 6(2011)581.

[19]M.Rotkiewicz,Extracta Math.20(2005)219.

[20]J.A.de Azc´arraga and J.M.Izquierdo,J.Phys.A:Math.Theor.43(2010)293001.

[21]A.Makhlouf,Chapter 4 in Non Associative&Non Commutative Algebra and Operator Theory,eds.C.T.Gueye and M.S.Molina,Proceedings in Mathematics&Statistics,Springer,Mulhouse 160(2016).

[22]J.Liu,A.Makhlouf,and Y.Sheng,Algebr Represent Theor.20(2017)1415.

[23]Y.Fregier,J.Algebra 398(2014)243.

[24]J.L.Loday,Enseign.Math.39(1993)269.

[25]J.L.Loday and T.Pirashvili,Math.Ann.296(1993)139.

[26]J.Liu,Y.Sheng,and Q.Wang,Commun.Algebra.46(2018)574.

[27]V.A.Dolgushev,Stable Formality Quasi-Isomorphisms for Hochschild Cochains,arXiv:math.K-Theory and Homology/1109.6031.