A Super mKdV Equation:Bosonization,Painlev´e Property and Exact Solutions∗

Bo Ren(任博) and Sen-Yue Lou(楼森岳)

1Institute of Nonlinear Science,Shaoxing University,Shaoxing 312000,China

2Center for Nonlinear Science and Department of Physics,Ningbo University,Ningbo 315211,China

3Shanghai Key Laboratory of Trustworthy Computing,East China Normal University,Shanghai 200062,China

1 Introduction

Super extensions of the standard integrable systems have caught a great deal of attention.Many equations such as Korteweg-de Vries(KdV),modified Korteweg-de Vries(mKdV),Sine-Gorden,Kadomtsev-Petviashvili hierarchy,and nonlinear Schrödinger equations were generalized into their supersymmetric counterparts.[1−7]For the KdV equation,it exists two kinds of extensions,one is the Kupershmidt’s or super version[1]and the other is the supersymmetric KdV equation proposed by Manin and Radul.[2]Supersymmetric version is invariant under the supersymmetry transformation while super version absences this property.[8]The field of the super version is considerable lacking compare with the supersymmetric version.[9]To generate super extensions of integrable systems and their properties is interesting and important problem.In this paper,we shall construct a systematic approach to generate new super integrable systems and an illustrative example is given in detail.

The remainder of the paper is organized as follows.In Sec.2,by embedding a fermionic symmetry to the original Lax representation,a new super mKdV(SmKdV)equation is constructed from the mKdV equation.In Sec.3,the SmKdV system is changed to a system of coupled bosonic equations based on the bosonization approach.The Painlev´e property of the coupled bosonic equations is studied by the standard singularity analysis.In Sec.4,some types of exact solutions can be explicitly found by means of the mapping and deformation method.The last section contains a brief summary and presents some interesting open problems.

2 A Scheme to Construct Super mKdV Equation

The mKdV equation reads

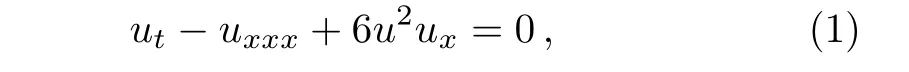
which is widely used in many different physical fields including ocean dynamics,fluid mechanics,and plasma physics.[10−11]

The Lax pair of Eq.(1)writes[12]

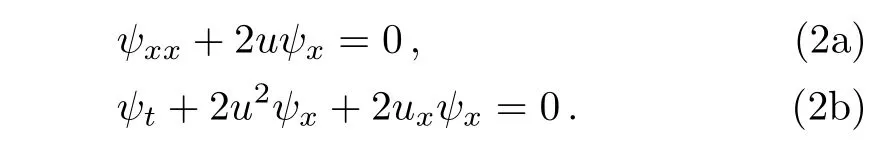
Propositionσu= ξξxis a fermionic symmetry of the mKdV equation,where ξ is a fermionic field and satis fies the following equation

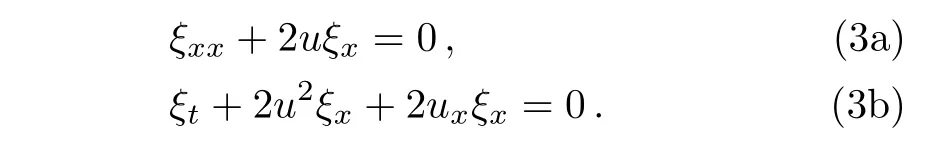
ProofBy substituting σu= ξξxinto the linearized of mKdV equation

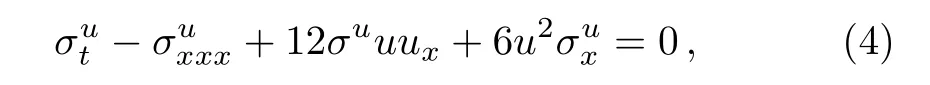
and letting ξ to satisfy(3),we can prove that σu= ξξxis a symmetry of the mKdV equation after detail calculations.

By means of above symmetry,the new super mKdV(SmKdV)equation can be obtained

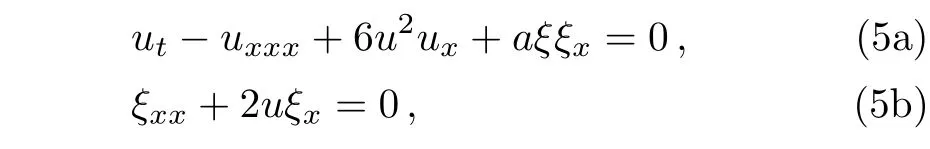
where a is arbitrary constant.Equation(5b)is just the Lax pair part of Eq.(3a).We can also write an SmKdV equation by selecting the other Lax pair part of Eq.(3b)

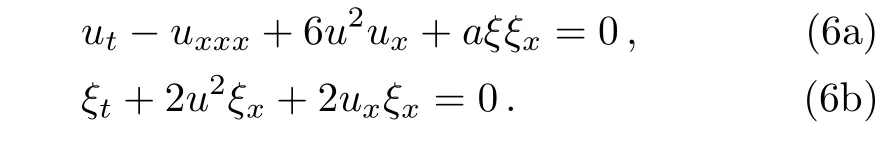
In this paper,we shall focus on the SmKdV system(5).

3 Bosionization Approach and Painlev´e Analysis for BSmKdV Equation

3.1 Bosonization Approach for BSmKdV Equation

For the SmKdV system(5),it exists the anticommutative fermionic field.To avoid the difficulties caused by the anticommutative fermionic field,a bosonization approach is introduced to deal with these problems.[13−15]

According to the bosonization approach,we expand the component fields u and ξ as[13−20]

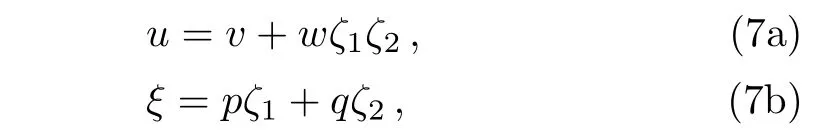
where ζ1and ζ2are two Grassmann parameters,while the coefficients v,p,q and w are four usual real or complex functions with respect to the space-time variables x and t.Substituting Eq.(7)into the SmKdV system(5),we obtain

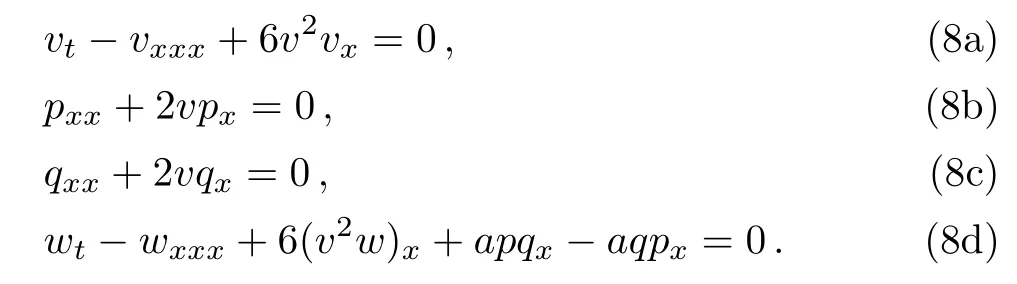
Equation(8a)is the usual mKdV equation,which has been widely studied(see Refs.[21–23]and the references therein). Equations(8b)–(8d)are linear homogeneous in p,q and w respectively.The system(8)is thus the BSmKdV system.These pure bosonic systems can be easily solved theoretically.This is just one of the advantages of the bosonization approach.

3.2 Painlev´e Analysis for BSmKdV System

In this part,we apply the Painlev´e test to the BSmKdV system(8).The system is called Painlev´e integrable if its solutions are single valued about an arbitrary singularity manifold.[24]According to the standard WTC(Weiss-Tabor-Carnevale)method,[24]the bosonic fields v,p,q and w expand about the singularity manifold ϕ(x,t)=0 as

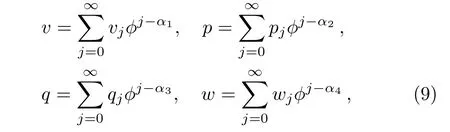
with vj,pj,qj,and wjbeing arbitrary functions of x and t.Balancing the most dominant terms,the constants α1,α2,α3and α4are positive integers,i.e.,1,1,1,2 respectively.Then,the recursion relations for the functions vj,pj,qj,and wjare obtained,the resonance values of j are given

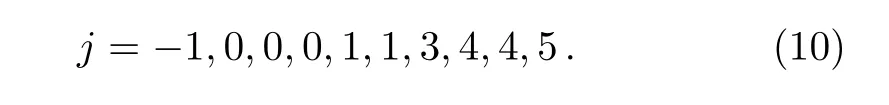
The next key for the Painlev´e analysis is the compatibility of the expansion coefficients. The resonance at j=−1 corresponds to the arbitrary singularity manifold ϕ.By substituting the Laurent expansion(9)into(8),we shall check the existence of sufficient number of arbitrary functions at other resonance values.Comparing the coefficients of the(ϕ−4,ϕ−3,ϕ−3,ϕ−5),the resonances at j=0,0,0 represent the arbitrary functions of p0,q0and w0,namely v0=ϕx.Gathering up the coefficients of(ϕ−3,ϕ−2,ϕ−2,ϕ−4)gives

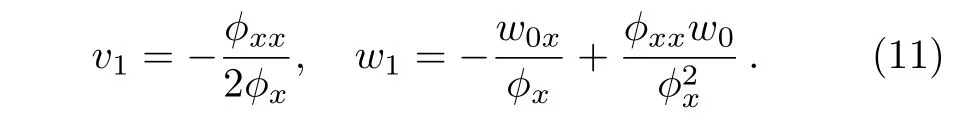
Absence of p1and q1prove that p1and q1are arbitrary.This corresponds to the resonance values at j=1,1.By collecting the coefficients of(ϕ−2,ϕ−1,ϕ−1,ϕ−3),we get

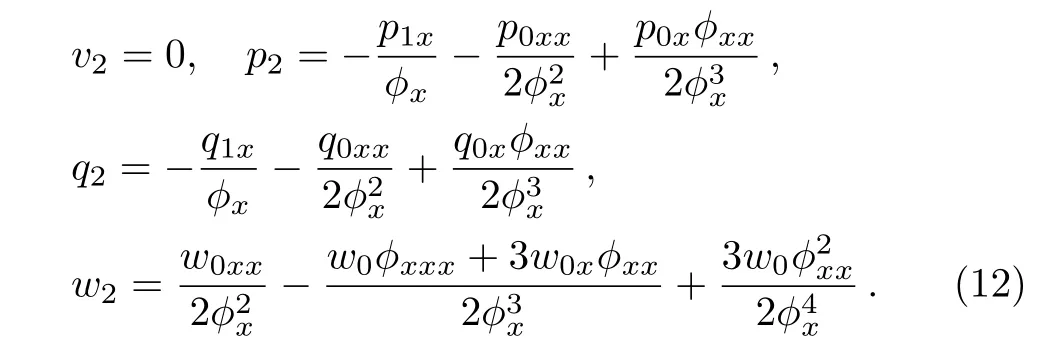
By collecting the coefficients of(ϕ−1,ϕ0,ϕ0,ϕ−2),we get

Above result proves v3is arbitrary.This corresponds to the resonance value at j=3.Proceeding further to the coefficients of(ϕ0,ϕ1,ϕ1,ϕ−1),absence of v4and w4prove that v4and w4are arbitrary.This corresponds to the resonance values at j=4,4.The values of v5,p5and q5are obtained by collecting the coefficients of(ϕ1,ϕ2,ϕ2,ϕ0).Absence of w5proves that w5is arbitrary.This corresponds to the resonance value at j=5.The resonance conditions are satis fied identically because the functions vj,pj,qjand wjare all determined by ten arbitrary functions ϕ,p0,q0,w0,p1,q1,v3,v4,w4,and w5.The number of arbitrary functions is same as the number of resonances.From the above considerations we deduce that the BSmKdV(8)is really Painlev´e integrable.

4 Traveling Wave Solutions by Mapping and Deformation Method

The mKdV equation has been widely studied in the literatures.[21−23]We can obtain the solutions of the BSmKdV equation by building the mapping and deformation relationship[14,16]between the solutions of the mKdV equation and BSmKdV equation. By introducing the traveling wave variable X=kx+ωt+c0with constants k,ω and c0,Eq.(8)is transformed to the ordinary differential equations(ODEs)

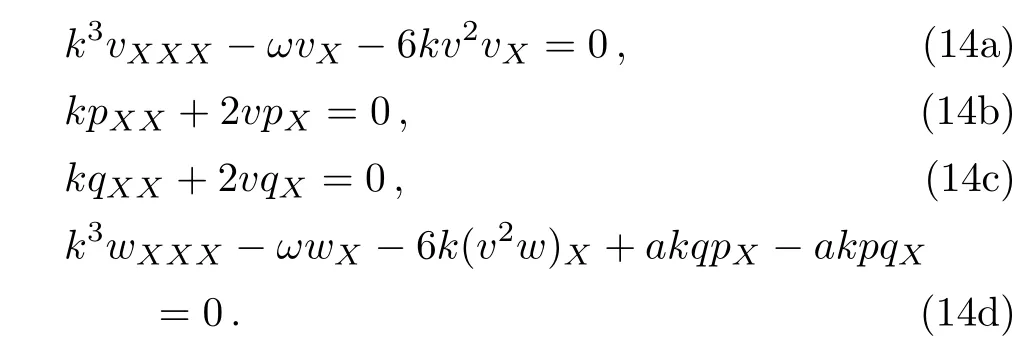
The expression for vXreads

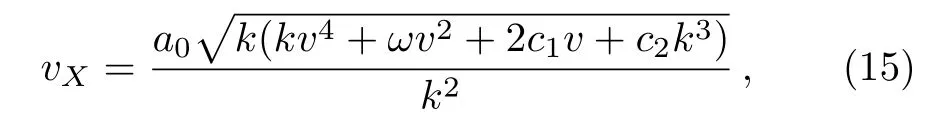
where c1and c2are the integral constants and=1.In order to get the mapping relationship between v and{p,q,w},we introduce the variable transformations

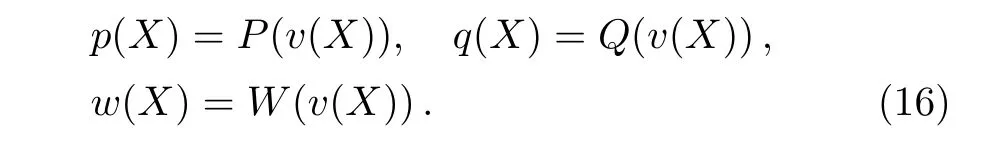
Using the transformation(16)and vanishing vXvia(15),the linear ODEs(10b)–(10d)become

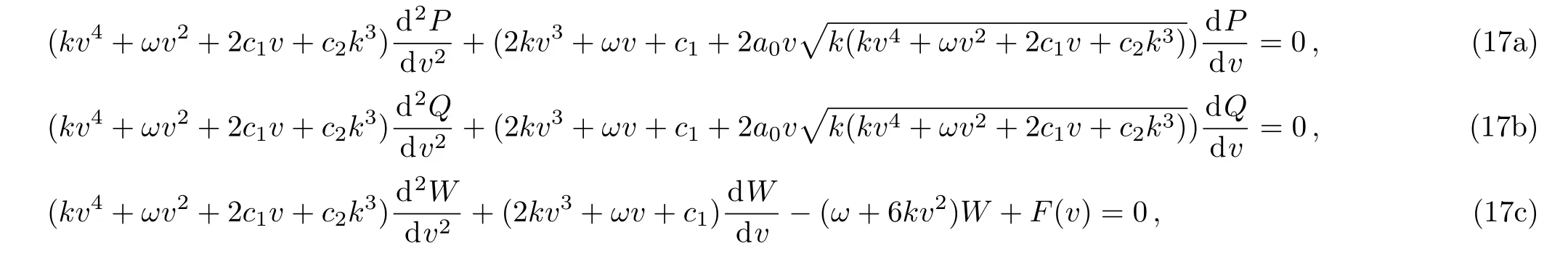
where

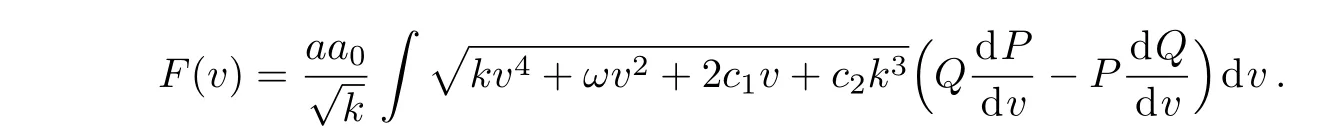
The mapping and deformation relations can be constructed by solving Eq.(17)directly

where ck(k=3,4,...,8)are arbitrary constants.

For a special case,c1=c2=c8=0,the solution(18)becomes

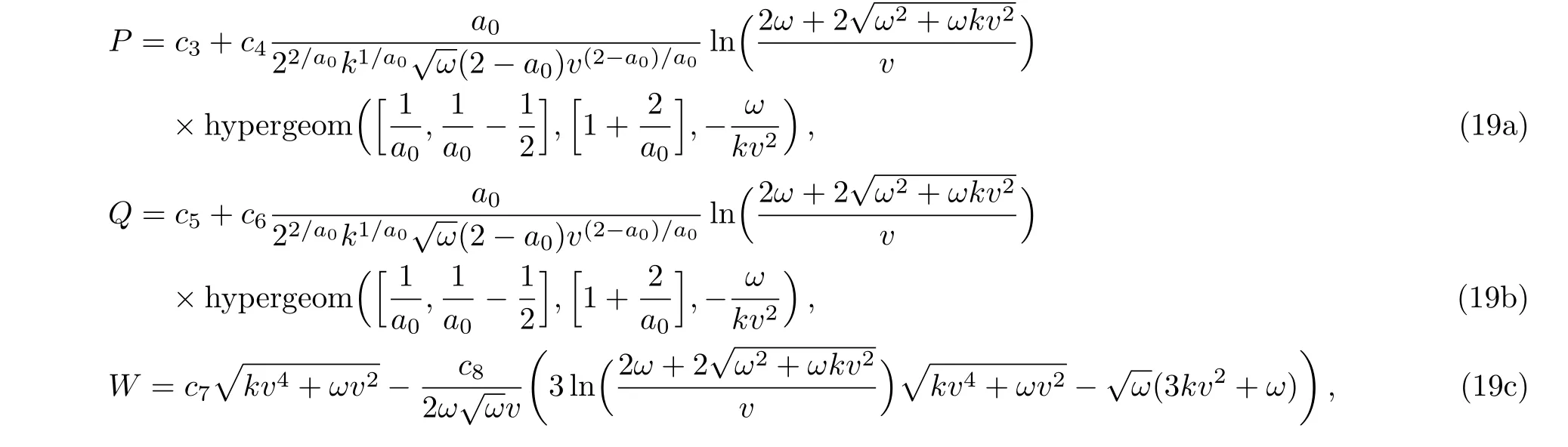
where hypergeom is the generalized hypergeometric function.The solutions of SmKdV equation(5)can be constructed by substituting Eqs.(16)and(19)into Eq.(7).

5 Conclusion

In summary,the symmetry related with the fermionic field for the mKdV equation is obtained by means of the Lax pair.Based on the symmetry of the fermionic form,new SmKdV equations are constructed.The bosonization approach is applied to the SmKdV equation.The fermionic field of the SmKdV equation is removed by the bosonization approach.The BSmKdV system is proved to possess Painlev´e property and to be completely integrable.Some exact solutions are studied by using the mapping and deformation method.

In this paper,we construct new super integrable systems by introducing a symmetry of the fermionic form.The self-consistent sources part is the nonlocal(bosonic form)symmetry of the self-consistent sources soliton equations[25−26]related with the Lax pair.[27−28]The new super integrable systems can be thus considered as the fermionic self-consistent sources soliton equations.The new integrable systems can be given by introducing the symmetry both the fermionic and bosonic forms.Besides,the symmetries of a model can be constructed with a strong symmetry(recursion operator)to act on some seed symmetry.[29]The new integrable systems can be given by embedding new symmetries.Those ideas can be applied to not only the mKdV system but also other models.On the other hand,some novel solutions for the usual nonlinear systems are widely studied.[30−34]It is interesting to show how those novel solutions of new super equations can be constructed in superspace.It is worthy of further study.

[1]B.A.Kupershmidt,Phys.Lett.A 102(1984)213.

[2]Y.I.Martin and A.O.Radul,Commun.Math.Phys.98(1985)65.

[3]M.Gurses and O.Oguz,Phys.Lett.A 108(1985)437.

[4]P.Mathieu,J.Math.Phys.29(1988)2499.

[5]I.Yamanaka and R.Sasaki,Prog.Theor.Phys.79(1988)1167.

[6]S.Ferrara,L.Girardello,and S.Sciuto,Phys.Lett.B 76(1978)303.

[7]G.H.M.Roelofs and P.H.M.Kersten,J.Math.Phys.33(1992)2185.

[8]L.L.Xue,D.Levi,and Q.P.Liu,J.Phys.A:Math.Theor.46(2013)502001.

[9]X.B.Hu,J.Phys.A:Math.Gen.30(1997)619.

[10]H.Schamel,J.Plasma Phys.9(1973)377.

[11]S.Y.Lou,B.Tong,H.C.Hu,and X.Y.Tang,J.Phys.A:Math.Gen.39(2006)513.

[12]M.C.Nucci,J.Phys.A:Math.Gen.22(1989)2897.

[13]S.Andrea,A.Restuccia,and A.Sotomayor,J.Math.Phys.42(2001)2625.

[14]X.N.Gao and S.Y.Lou,Phys.Lett.B 707(2012)209.

[15]B.Ren,J.R.Yang,P.Liu,and X.Z.Liu,Chin.J.Phys.53(2015)080001.

[16]B.Ren,J.Lin,and J.Yu,AIP Advances 3(2013)042129.

[17]X.N.Gao,S.Y.Lou,and X.Y.Tang,J.High Energy Phys.05(2013)029.

[18]B.Ren,J.Lin,J.Y.Le,et al.,Commun.Theor.Phys.68(2017)170.

[19]B.Ren,Open Phys.13(2015)205.

[20]B.Ren,X.N.Gao,J.Yu,and P.Liu,Open Math.13(2015)502.

[21]C.Q.Dai,J.M.Zhu,and J.F.Zhang,Chaos,Solitons&Fractals 27(2006)881.

[22]Z.Y.Yan,Commun.Nonlinear Sci.Numer.Simul.4(1999)284.

[23]H.Trikia and A.M.Wazwaz,Appl.Math.Comput.214(2009)370.

[24]J.Weiss,M.Tabor,and G.Carnevale,J.Math.Phys.24(1983)522.

[25]V.K.Met’nikov,Commun.Math.Phys.120(1989)451.

[26]D.J.Zhang,J.Phys.Soc.Jpn.71(2002)2649.

[27]X.R.Hu,S.Y.Lou,and Y.Chen,Phys.Rev.E 85(2012)056607.

[28]X.P.Cheng,S.Y.Lou,C.L.Chen,and X.Y.Tang,Phys.Rev.E 89(2014)043202.

[29]S.Y.Lou,Phys.Lett.B 302(1993)261.

[30]Y.H.Hu and Q.Y.Zhu,Appl.Math.Comput.305(2017)53.

[31]Y.H.Hu and Q.Y.Zhu,Nonlinear Dynam.89(2017)225.

[32]Q.Y.Zhu,J.X.Fei,and Z.Y.Ma,Z.Naturforsch.A 72(2017)795.

[33]B.Ren,X.P.Cheng,and J.Lin,Nonlinear Dynam.86(2016)1855.

[34]B.X.Guo,Z.J.Gao,and J.Lin,Commun.Theor.Phys.66(2016)589.