基于神经网络的液压材料试验机系统自适应PID控制研究

徐杭东，麦云飞

(上海理工大学 机械工程学院，上海 200093)

0 引 言

液压材料试验机是测定金属材料、非金属材料、机械零件、工程结构等的机械性能、工艺性能、内部缺陷和校验旋转零部件动态不平衡量的精密测试仪器。液压控制系统可以对位移、速度、力等任意研究对象进行控制。结合了电气和液压两方面的电液伺服系统，拥有高的控制精度、较快的响应速度、较大的输出功率以及处理信号灵活、各类参量反馈简便等优势，适合在负载质量大以及响应速度要求快的场合使用，在航空、航天、冶金、交通等领域具有广泛的应用。

目前，液压伺服控制设计主要考虑以下：

(1)由于复杂的工作条件和工作内容，系统的参数变化较大，还受外负载干扰及交联耦合的影响；

(2)非线性的影响，特别是在高压、重载下这种非线性和不确定性对控制性能的影响尤为突出。

随着液压材料试验机在开发新材料和材料质量控制等方面的应用越来越广泛，对其精度的要求也越来越高；而控制系统对试验机的性能有重要影响，因此对试验机控制系统的研究对试验机性能的提高有重要作用[1]。

然而对于液压材料试验机这种高阶控制以及非线性系统，普通PID控制不理想，而神经元控制由于其本身具有自适应特点，却能够发挥相对较好的控制作用。

本研究将在计算机技术和智能控制技术发展的基础上，利用神经网络控制算法来改善被控对象的非线性特性，以提高其控制精度[2-6]。

1 建模与分析

电液位置伺服系统常用的指令元件有信号发生器、电位器、计算机等器件，指令单元会根据系统动作的要求发出相应的电压控制信号[7]。

本研究对象(材料试验机)的指令装置是计算机，通过计算机软件发出相应的指令，D/A转换器转换成电压控制信号；检测反馈装置用的是位移传感器；采用位移传感器检测输出位置并转换为电压信号，与指令信号进行比较，获得偏差信号，从而构成系统闭环反馈结构；采用电液伺服阀作为系统的控制元件；执行机构为液压缸。

本次研究对象模型主要由PID控制器、伺服放大器、电液伺服阀、位移传感器、阀控缸等组成，材料试验机位置控制系统如图1所示。

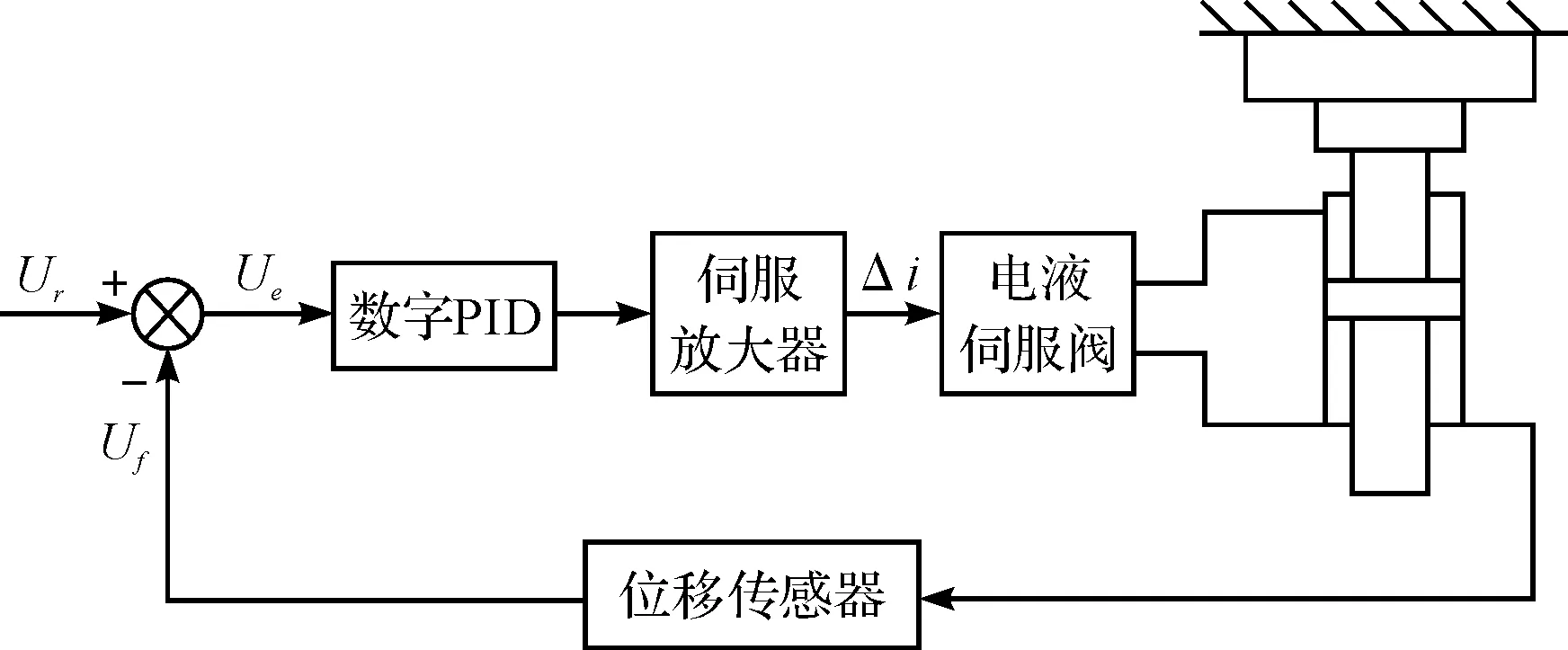
图1 材料试验机位置控制系统

本研究通过对控制系统的分析对其建立数学模型，得到典型位置反馈系统的方框图，并且对研究对象进行简化，假设外负载干扰力Fl为0，此外有弹性负载的情况(阀控液压缸中弹性负载较为常见，液压材料试验机原理是施加一定的力作用于材料使之变形，假设将负载看成弹性负载，并且将被测材料看成是硬弹簧)[8-9]，反馈系统如图2所示。

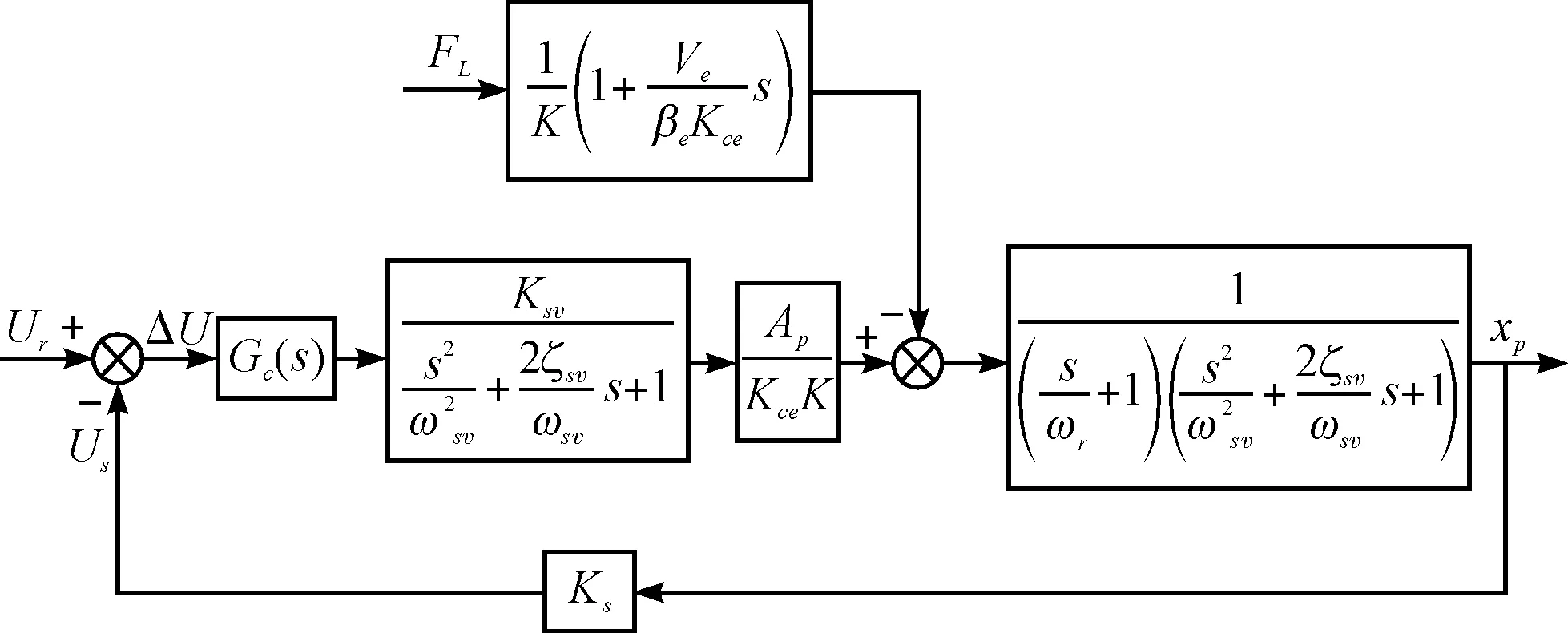
图2 典型位置反馈系统

得到系统的开环传递函数为：

(1)

经过设备的选取和计算得到：伺服放大器的比例增益为Ka=20 mA/V；流量增益为Ksv=3.33×102m3(A·s)；位移反馈系数为；Ks=300 V/m，液压缸的有效面积为；Ap=8.48×10-3m2，弹性负载刚度为K=1.0×107N/m；压力流量系数为；Kce=1.587×10-11m3·s-1/Pa，惯性环节的转折频率为wr=2.2 rad/s；伺服阀的固有频率为wsv=100 Hz；阻尼系数为ξsv=0.63，ζn=0.2。

经过计算，建立系统的传递函数仿真模型，并做出系统开环bode图以及闭环阶跃响应，分析系统的稳态性能。

系统开环bode图以及闭环阶跃响应如图3所示。

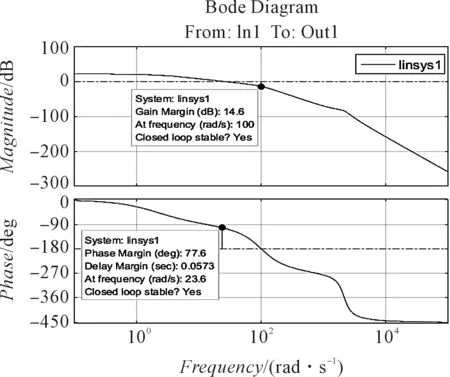
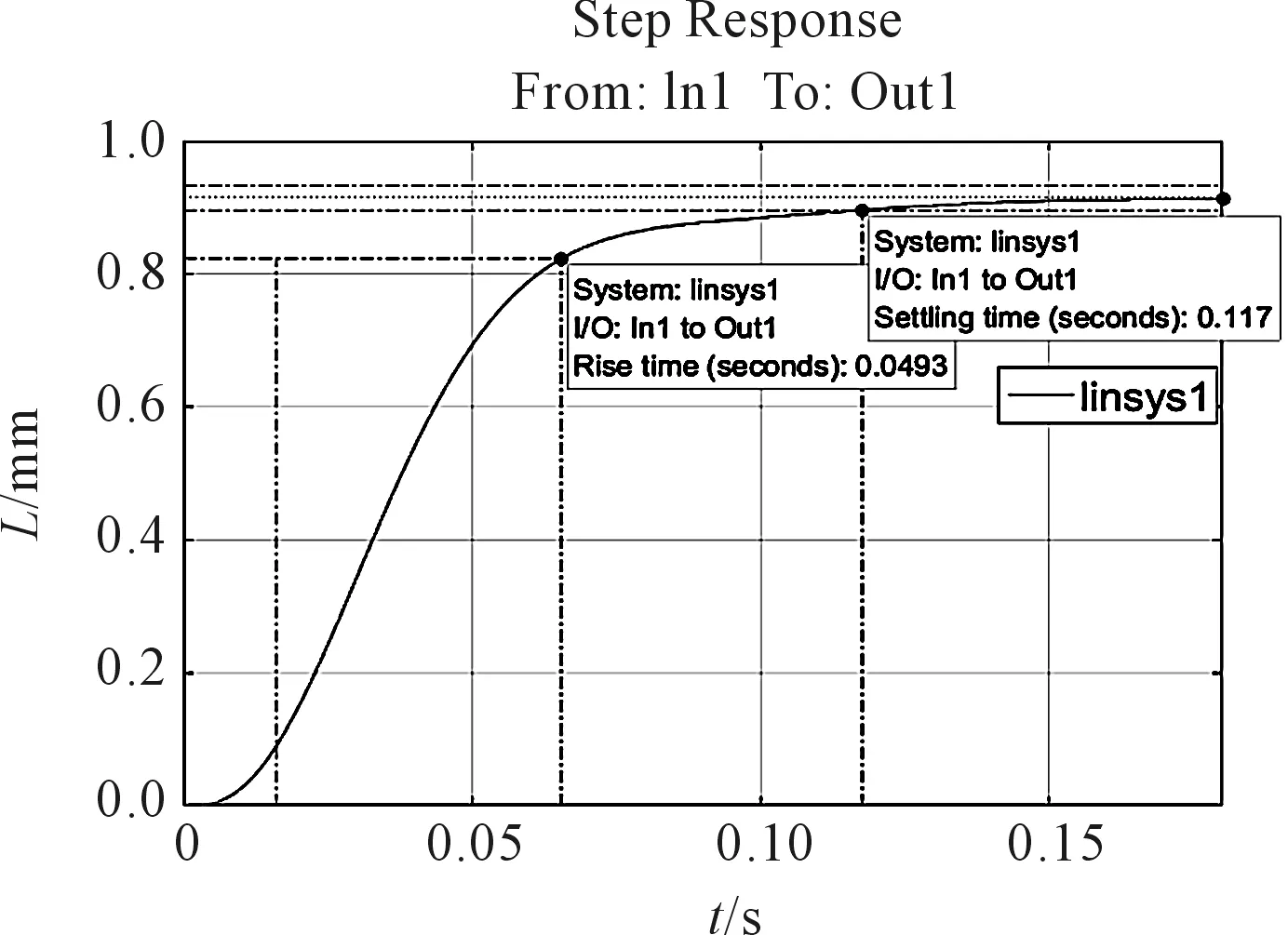
图3 系统开环bode图以及闭环阶跃响应

能够看出其幅值裕度为14.6 dB，相位裕度为77.6°。一般来说，为了获得较好的控制作用，要求系统具有一定大小的稳定裕度，一般幅值裕度大于6 dB，相位裕度在之间。

该系统的相位裕度大、系统响应慢，并且通过仿真系统的阶跃响应可以看出，系统并不能达到最终的稳定值，系统的稳态误差较大，所以系统具有适当校正的需要[10]。

2 Ziegler-Nichols法PID整定

由于根轨迹设计和Bode图设计不能直接用于PID的整定，Ziegler与Nichols发展了PID调节器的设计方法，该方法是假设Ti=∞，Td=0，只采取比例控制，使得Kp从0连续增至临界Kc，Kc是使系统首次输出为临界状态，等幅振荡时的增益值。

其他PID参数是根据Ziegler-Nichols调整法则所确定的，如表1所示。

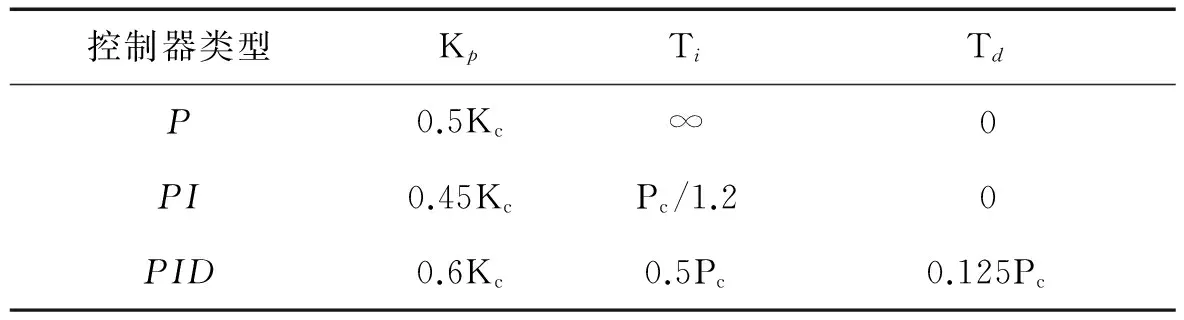
表1 Ziegler-Nichols PID参数整定

其中：

(2)

式中：Pc—临界振荡周期；Kc—系统临界振荡时的比例系数值；wm—临界振荡频率。

在Matlab仿真软件中，系统的根轨迹如图4所示。

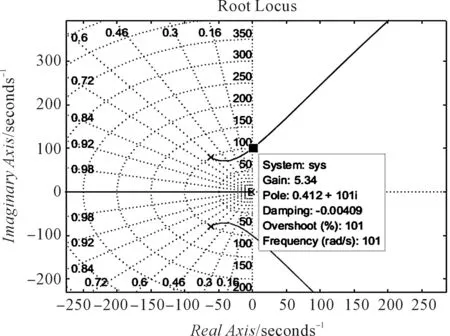
图4 根轨迹

如图4所示的根轨迹图，Kc值为与虚轴交点的增益值5.34，临界振荡频率wm为101 rad/s。通过参数整定表格中的公式计算得到PID的值，在Simulink中进行仿真。

阶跃输入设置L为3 mm，经过Matlab仿真得到经过整定后的PID控制的系统阶跃响应与原系统的的阶跃响应比较图，如图5所示。

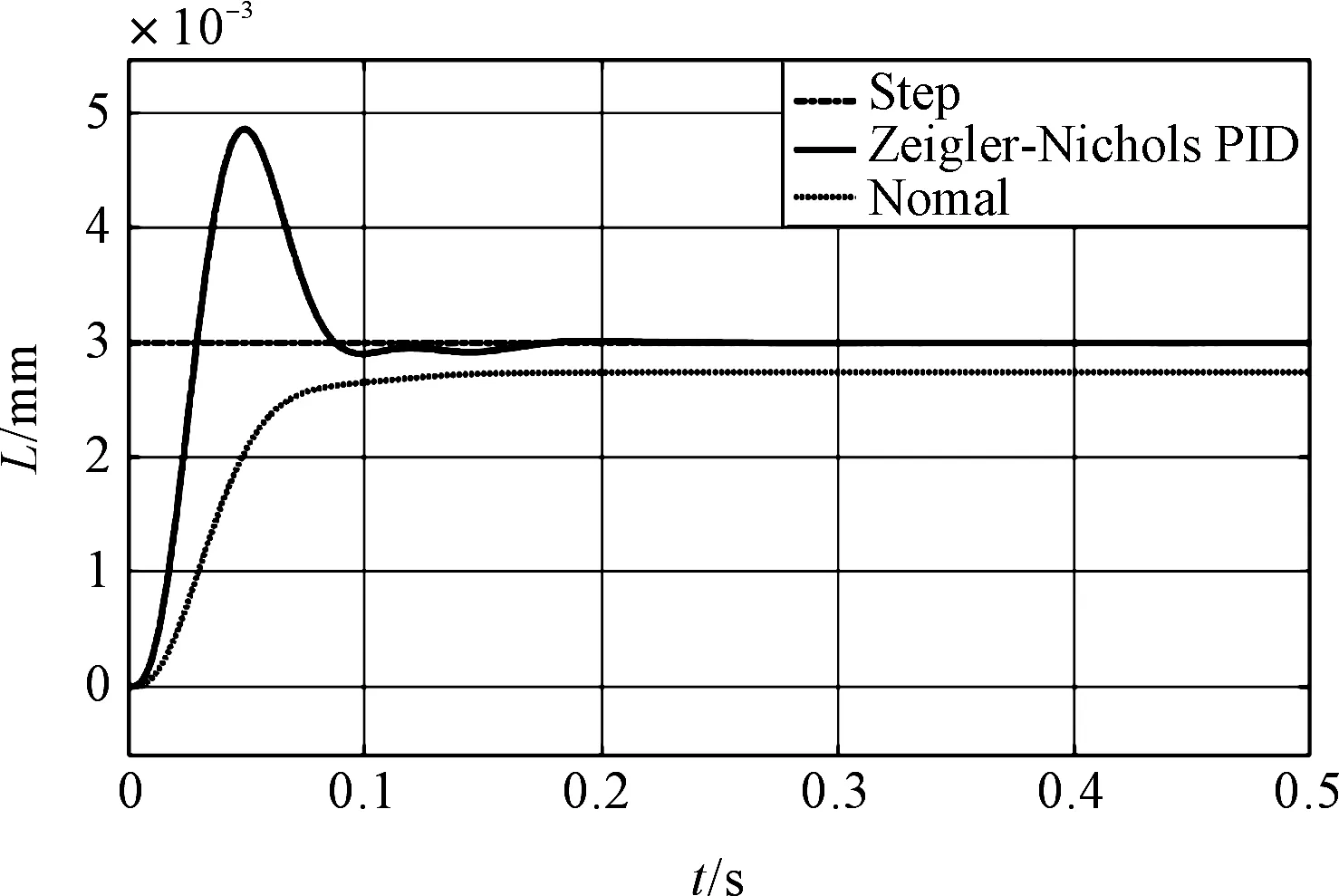
图5 Ziegler-Nichols法PID整定后的阶跃响应

由图5可以看出：传统的PID控制可以使系统反应的快速性增加，是稳态误差减少，但是发现其超调量过大，在精密位置控制过程中，超调量过大可能造成巨大的冲击，因而需尽量避免。

3 基于s函数的单神经元PID控制

3.1 实验方法

3.1.1 单神经元控制及其算法

将神经网络控制和传统的PID调节器结合起来，能够解决一般难以实时参数整定和难以对某些复杂过程有效控制的问题。

传统的PID连续控制规律是：

(3)

本文PID所采用的是增量式的PID控制(所需的控制量仅是控制量的增量Δu(k)如下式所示：

Δu(k)=KP[e(k)-e(k-1)]+KIe(k)+

KD[e(k)-2e(k-1)+e(k-2)]

(4)

单神经自适应PID控制结构原理如图6所示。

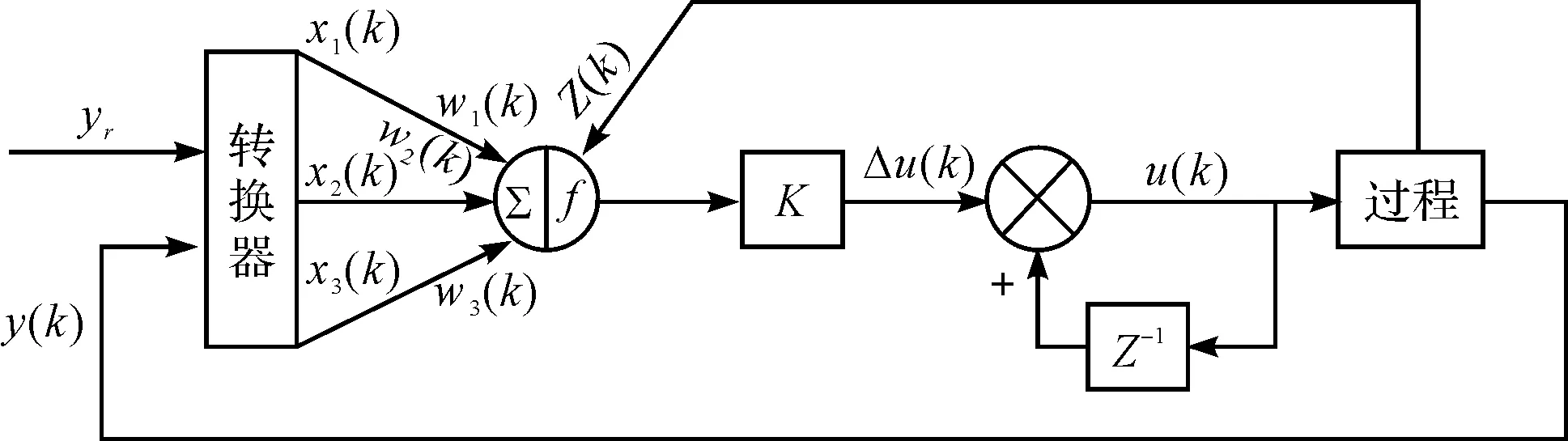
图6 单神经元自适应控制结构图

控制学习所需的过程量由转换器输出，u(k)是通过关联搜索以及自学习产生，yr是给定的固定值，y(k)为系统的输出，通过转换器转换后得到系统学习所需的过程量：x1(k)、x2(k)、x3(k)，如下式所示：

x1(k)=e(k)，x2(k)=Δe(k)，x3(k)=Δ2e(k)

(5)

式中：Z(k)=yr(k)-y(k)—系统的递进信号，w1(k)、w1(k)、w1(k)—对应x1(k)、x2(k)、x3(k)的权值系数；K—神经元比例系数，K>0。

3.1.2 有监督的Hebb学习算法

神经网络的学习规则即为调节神经元之间连接权值的规则。本文选用的是有监督的Hebb学习规则，如下式所示：

Δwi=ηiZ(k)u(k)xi(k) (i取1,2,3)

(6)

式中：η1，η2，η3—比例系数、积分系数、微分系数的学习速率。

对上述的学习算法进行规范化处理，可以保证该学习算法的收敛性与鲁棒性，如下式所示：

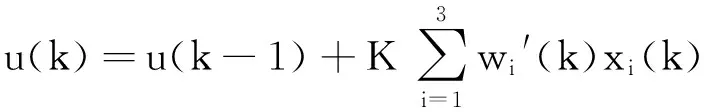
(7)

3.1.3S函数的编写

直接简单的使用SIMULINK也无法对单神经网络控制进行模拟。此时，可以引入控制系统的S函数，通过编写S函数将算法进行描述[11-12]。

编写基于Hebb学习算法的控制系统S函数：

部分算法编写如下所示：

functionsys=mdlUpdate(t,x,u,1,2,3)
sys(1)=x(1)+1*u(1)*u(4)*u(1);
sys(2)=x(2)+2*u(1)*u(4)*u(2);
sys(3)=x(3)+3*u(1)*u(4)*u(3);
functionsys=mdlOutputs(t,x,u,K)

xx=[u(1)-u(2)u(1)u(1)+u(3)-2*u(2)];
sys=[u(4)+K*xx*x/sum(abs(x));
x/sum(abs(x))];

3.2 实验结果与分析

本研究经过较长时间的调试，搭建Simulink模型。选取神经元的初始值为(6.5 0.5 0.01)，取采样时间为0.001 s，双击S函数模块输入神经元的学习速率η1=0.5，η2=0.5,η3=0.5。

建立好的模型包括主系统和Single Neuron PID Controller子系统，如图7所示。

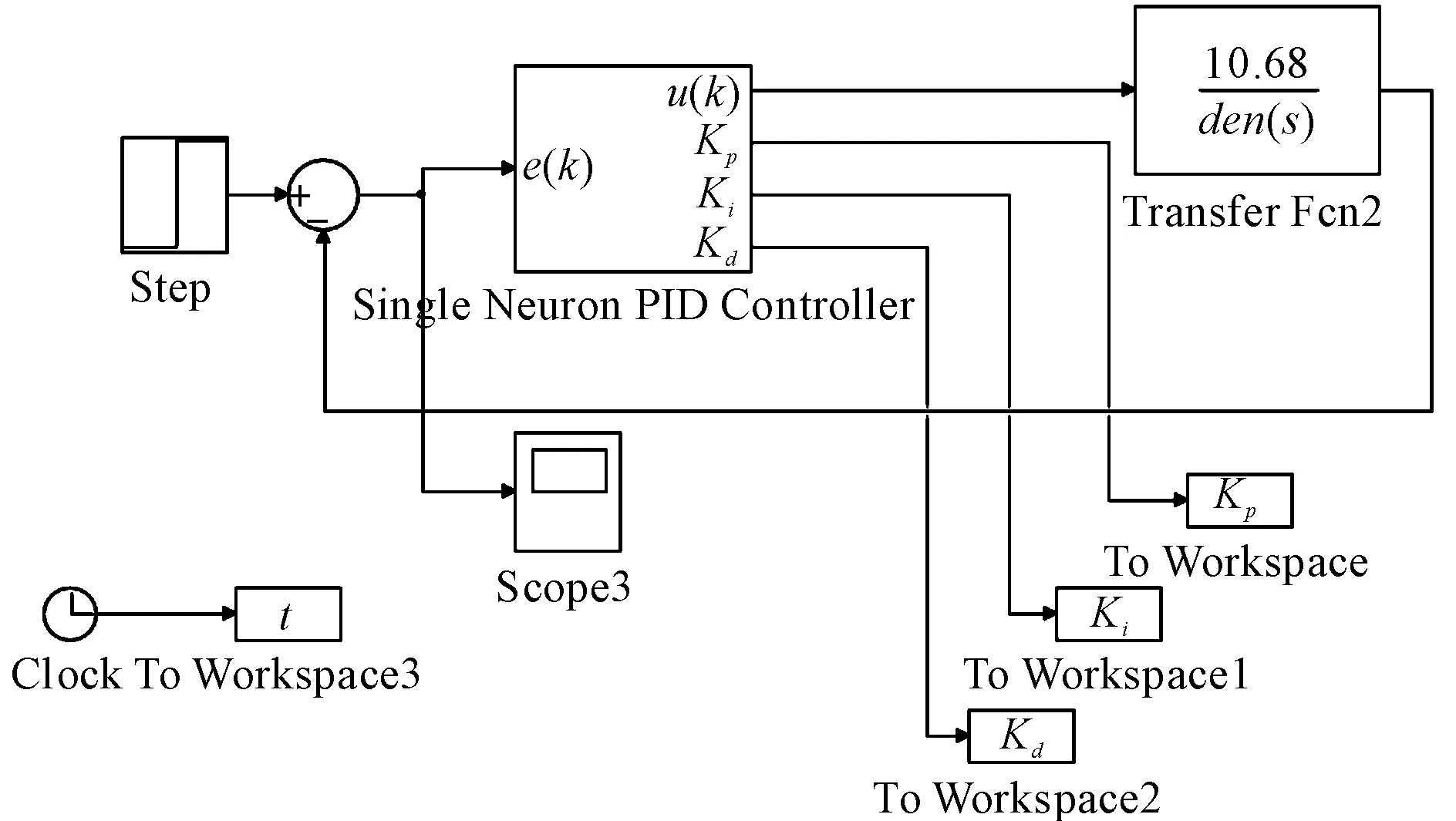
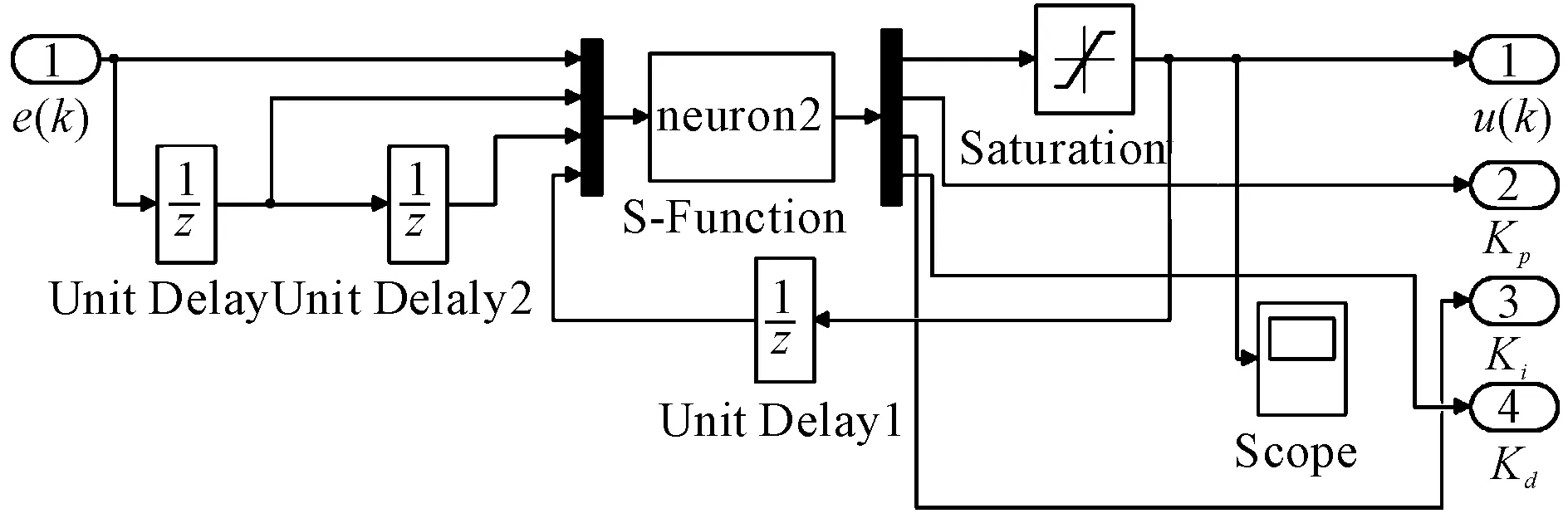
图7 单神经元自适应PID控制

阶跃输入L为3 mm。系统的阶跃响应如图8所示。

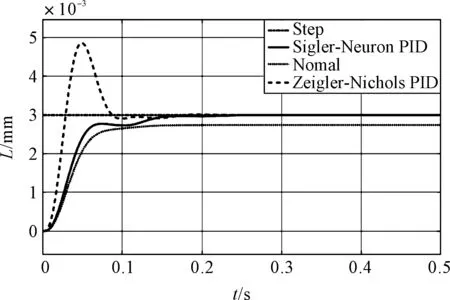
图8 系统阶跃响应

Kp、Ki、Kd3个参数随时间的变化自我学习调整的曲线如图9所示。

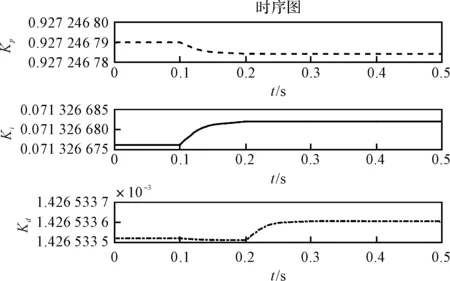
图9 Kp、Ki、Kd参数的变化曲线

通过分析，由图可以得出，运用Ziegler-Nichols法PID整定，将传统PID控制器应用于电液位置伺服控制，结果显示传统PID在一定程度上可以达到系统的稳定控制要求，但是控制效果不理想，超调量大、参数整定困难。编写S函数并搭建单神经元PID控制器的Simulink仿真模型，分析能够看出PID的3个参数具有自适应能力，控制系统响应快，超调小，稳态误差小，动态性能好，并提高了系统工作性能，可以较好地优化解决材料试验机运行过程中出现的精度低、稳定性差的问题[13-15]。

4 结束语

本研究介绍了电液位置伺服系统的工作原理，建立了材料试验机的数学模型，分析了系统出现精度低、稳定性差问题的原因，结果表明：因为系统稳态误差大，系统的相位裕度较大。为了优化系统的动态性能，本研究运用了传统的PID控制，并利用Matlab进行了实验仿真，但出现了系统超调量过大的问题；为此，笔者开发运用了神经网络算法控制原理，搭建了Maltlab/Simulink仿真模型，通过控制参数，实验得到采用神经网络控制的系统具有更好的稳定性和鲁棒性[16-19]。

基于神经网络的控制算法也广泛应用在一些复杂的非线性控制领域，因此本研究对其他控制系统优化也具有一定的参考意义和实用价值。

参考文献(References):

[1] 杨 敏.电子万能材料试验机单神经元PID控制系统研究[D].扬州：扬州大学机电工程学院，2012.

[2] 刘 迪.基于神经网络的PID控制[D].哈尔滨：黑龙江大学机电工程学院，2008.

[3] 韦亚娟.电液伺服系统的神经网络自整定PID控制策略研究[D].秦皇岛：燕山大学机械工程学院，2009.

[4] 陈 梦，高 强，余世航，等.某电液伺服系统的冗余控制[J].兵工自动化，2017，36(11)：1-3，7.

[5] 林瑞全,邱公伟.基于S函数的神经元PID控制器Simulink仿真模型[J].中国仪器仪表，2001(6)：4-5.

[6] 杨 勇.步进梁液压控制系统PID参数的整定[J].液压与气动，2015(4)：113-117.

[7] 孙志富.PID控制器参数整定Matlab/Simulink仿真[J].科技传播，2010，27(2)：95-111.

[8] 杜晓婷,方 飞.基于Simulink的单神经元自适应PID控制器研究[J].赤峰学院学报：自然科学版，2015，31(4)：16-17.

[9] 杨 艺,虎恩典.基于S函数的BP神经网络PID控制器及Simulink仿真[J].电子设计工程，2014，22(4)：29-31.

[10] 吴 伟,晏梦云,魏航信.基于神经网络的PID控制及其仿真[J].现代电子技术，2009，32(10)：143-145.

[11] 曾豪勇,周思柱,易文君.基于Matlab的增量式PID参数整定[J].工业控制计算机，2014，27(6)：69-70.

[12] 薛定宇.控制系统计算机辅助设计——Matlab语言及应用[M].2版.北京：清华大学出版社，2006.

[13] 周建刚.液压伺服系统PID控制器参数的优化[D].无锡：江南大学通讯与控制工程学院，2009.

[14] 张学燕,高培金,刘 勇.BP神经网络PID控制器在工业控制系统中的研究与仿真[J].自动化技术及应用，2010，29(5)：9-11.

[15] 朱逢锐,林玉娥.基于RBF神经网络的PID自校正控制研究[J].电脑知识与技术，2016，12(25)：155-157.

[16] 靳红涛,焦宗夏,周汝胜,等.基于神经网络PID的冗余伺服系统自适应控制[J].机械工程学报，2008，44(12)：249-253.

[17] 蔡洪旺，袁宇斌.基于称量自校正补灌控制系统研究设计[J].包装与食品机械，2017(1)：40-42.

[18] 魏跃斌，陈惠贤，张小奇，等.基于先进PID控制的液压同步系统研究[J].液压气动与密封，2016(1)：20-22.

[19] 何芝强.PID控制器参数整定方法及其应用研究[D].杭州：浙江大学化学工程与生物工程学院，2005.