Health evaluation method for degrading systems subject to dependent competing risks

ZHAO Shuai,MAKIS Viliam,CHEN Shaowei,and LI Yong

1.School of Electronics and Information,Northwestern Polytechnical University,Xi’an 710072,China;2.Department of Mechanical and Industrial Engineering,University of Toronto,Toronto M5S 3G8,Canada

1.Introduction

Recently,prognostics and health management(PHM)[1]has emerged as a promising technology with considerable benefits for various degrading systems. One of the essential objectives of PHMis the health assessment of systems subject to condition monitoring,thereby helping practitioners to optimize spare part requirements, develop optimal maintenance policies,and maximize the availability of degrading systems in critical applications[2].

To guarantee safety requirements,advanced sensors are applied to degrading systems to monitor their real time performance indicators.For an engineering system subject to condition monitoring,a soft failure will be encountered if the implemented sensors indicate that the degradation signal exceeds the predefined critical level.It is also possible that the system functionality stops abruptly due to the physical failure,which is termed as the hard failure[3].In such cases,the degrading systems are considered to be subject to the competing risks,i.e.,a soft failure and a hard failure.Literature review indicates that competing risks[4]have received modest attention.Zhao et al.[5]investigated the competing risks problem where a Brownian motion process was applied to model the soft failure and a Weibull distribution was used to describe the occurrence of thehard failure.In[6],Bocchetti et al.put forward a method to characterize the competing risks for cylinder liners applied in Sulzer RTA 58 engines,where the wear degradation failure,i.e.,the soft failure was driven by a stochastic process,and the thermal cracking failure,i.e.,the hard failure was characterized by a Weibull distribution.For a long-storage-short-run system,Guo et al.[7]studied a competing risks model where the soft failure was driven by a Gamma process with a predefined critical level and the hard failure was described by a Weibull distribution.Considering both the soft and the hard failure modes in practical engineering systems,Wang and Gao[8]established a reliability evaluation method which was verified for an aircraft engine.The degradation process was characterized by a non-homogeneous Gamma process and the time to hard failure was described by a Weibull distribution.

Note that one of the common features of the aforementioned works is that there is no dependent relationship between the soft and the hard failures.However,in most practical applications,the occurrence of the hard failure depends not only on the operational time,but it is also more likely to occur when the degradation level is higher[9,10],which indicates that the soft failure and the hard failure are dependent.Thus,the independence assumption of the soft and hard failure modes may cause underestimation or overestimation of the system health condition.Recently,there has been a growing interest in modeling dependent competing risks of various failure modes for system health evaluation.Guo et al.[11]proposed a copula function method for a system subject to dependent competing risks driven by two degradation processes and random shocks.In[12],Huynh et al.applied a Gamma process to characterize the system degradation failure.To describe the dependent relationship,the degradation level was assumed to be a factor in the shock failure modeling.Other models considering the dependent failure modes can also be found in[13,14].For the competing risks of the dependent soft and hard failures, the model formulation and evaluation are quite challenging and have not been well addressed in the literature.Thus,much work should be carried out to facilitate the health assessment for degrading systems subject to the competing risks of dependent soft and hard failures.

Motivated by the lack of research in this area,a health evaluation method for degrading systems subject to competing risks where a dependent relationship exists between the soft and hard failures is proposed.The degrading system is considered to be in the failure state when either the degradation process exceeds the predefined critical level or the system’s functionality stops abruptly.The degradation process is characterized by a non-stationary Gamma process[15]considering the time-varying deterioration rate encountered in real systems.The dependent relationship between the soft and hard failures is modeled by incorporating the degradation process into a Cox’s proportional hazards(PHs)model as a covariate process to characterize the failure rate of time to hard failure.A transition probability-matrix method is developed which enables the analysis of the proposed model and derivation of the explicit formulas for the health characteristics.The calculation of the health characteristics can then be performed with simple operations on the transition probability matrix,which is quite computationally efficient and can support the online health evaluation.

This paper presents a comprehensive health assessment method for degrading systems subject to condition monitoring and dependent competing risks,which distinguishes it significantly from our preliminary work[16]presented at 2016 Prognostics and System Health Management Conference in two directions.First,the methodology development is more systematic,and theoretical details for the derivation and calculation of the health characteristics are presented.Second,the applications for the online health assessment and the implications for real applications,which were not included in[16],are illustrated and discussed.

The remainder of this paper is organized as follows.In Section 2,we present the modeling method of the dependent soft and hard failures as well as a transition probability-matrix method which enables the model analysis and further development.Section 3 presents the explicit formulas for the related health characteristics.To show the effectiveness of the proposed method,a numerical study is carried out in Section 4.Finally,the conclusions are given in Section 5.

2.Degradation and failure process modeling

Before presenting the details of the proposed method, several assumptions adopted in this paper can be summarized as follows:

(i)When the degradation signal reaches the predefined critical level,the soft failure occurs,which is observable.

(ii)The degrading system may stop its functionality abruptly,i.e.,it is subject to hard failure.

(iii)The degrading system will stop working when the operating time reaches a maximum allowable age limit,i.e.,the end of its whole life cycle.

Practically,these assumptions can be reasonably justified,and an example is a degrading system equipped with expendable devices such as fuses or canaries[17].When the degradation signal exceeds the predefined critical level,the corresponding protecting actions will be activated and the system is able to notify the user about its health state automatically.In this case,the system runs into the soft failure state and its residual life expires.On the other hand,the degrading system,especially the critical one,is not allowed to operate any longer when the operation time is larger than the maximum allowed time limit.

2.1 Model formulation

Assume that a degrading engineering system is subject to condition monitoring.For each system,there exists some observable degradation process related to its health condition that can be monitored along with the system operation.In most cases,the degradation process is monotonically increasing or decreasing and it is not self-recoverable without any interventions or maintenance,e.g.,the crack growth of bearings.Considering the monotonicity of the degradation process,we choose the Gamma process[18],which is considered as an accumulation of a sequence of small positive increments,to model the system degradation.Suppose that the degradation processis characterized by a Gamma process.Thus,the probability density function(PDF)of the degradation process can be expressed as

wherek(t)＞0 is the shape parameter,θ＞0 is the scale parameter,andΓ(k(t))is the Gamma function.It should be noted that the shape parameterk(t)depends ont,which suggests that the temporal variability of the degradation rates is able to be easily incorporated into the degradation process modeling.DenoteTsas the soft failure time to represent the time instant whenX(t)exceeds the critical levelY.Based on the properties of the Gamma process,the probability distribution of the soft failure time[18]can be written as

whereΓ(a,x)is the incomplete Gamma function.

To combine the operating age and the degradation information in the modeling of the hard failure,a Cox’s PH model is selected to describe the failure rate of the time to hard failure.Generally,the Cox’s PH model is composed of two multiplicative factors,i.e.,a functionh0(t)which describes the baseline hazard at timet,and a positive functionψ(X(t);β)which is applied to incorporate the effect of covariates.Thus,the hazard function can be expressed as

whereβdenotes the regression coefficient andX(t)is the covariate process which can be either an external environmental variable or an internal diagnostic variable.In this paper,to show the effect of the degradation on the system failure,the degradation processX(t)is used in the Cox’s PH model as a time-varying covariate process.Using this model,the operating age and the degradation information can be integrated to describe the hard failure mechanism.In this way,the dependent relationship between the soft and hard failures is modeled by incorporating the degradation process in the Cox’s PH model.Thus,the PDF of the hard failure timeThis given by the following formula:

It can be seen that the probability distribution of the competing failure time for the soft and hard failures can be explicitly expressed by(2)and(4),respectively.The reliability function for a system is then given by

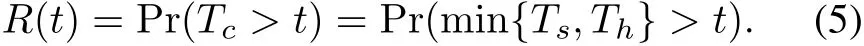
Nevertheless,considering the non-stationary characteristic of the degradation process and dependent relationship between failure modes,the straightforward derivation and evaluation of(5)are quite challenging,or even impossible.Moreover,the conditional health characteristics given the monitoring degradation state and the operation age, such as the conditional reliability function(RF),conditional mean residual life (MRL) [19], and the corresponding confidence interval which are essential for the online health assessment,are also quite challenging to develop and evaluate.To overcome these challenges,a method is proposed to enable the derivation and calculation of the health characteristics.

2.2 Transition-probability-matrix method

In[20],Brook and Evans proposed a method based on the Markov chain to calculate the average run length(ARL)in quality control.Considering the similarities between ARL and MRL,a method inspired by[20–22]is proposed to enable the above model evaluation and thereby calculate health characteristics for degrading systems subject to dependent soft and hard failures.

To consider both the soft and hard failures simultaneously,we propose a joint processV(t)=(X(t),Tc＞t)(t∈R+)to integrate the degradation processX(t)and the failure timeTc.For any given time instants 0=t0＜t1＜t2＜···＜tn-1＜tn＜∞,the transition probability of the joint process is able to be expressed as

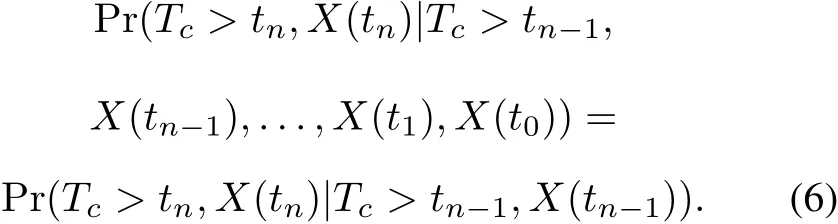
It can be seen that the joint processV(t)possesses the Markov property.With the joint degradation process,both the degradation behavior and failure information including the soft failure timeTsand the hard failure timeThcan be integrated into(6)and their evaluations can be performed together.Note that both the degradation process and the monitoring time axis in(6)are continuous and thus the state space of the joint process is in finite.To make the model evaluation feasible,the state space of the joint process needs to be finite and a twofold discretization technique is proposed.

First,we discretize the continuous degradation processX(t)into several discrete states.Particularly,it is supposed that such a continuous degradation process is approximated and represented as a Markovchain whose state spaceΩconsists ofM+1 states.Denote the state spacewhereS0represents the“good as new”state andSM-1represents the worst operation state.When the system deteriorates into the absorbing stateSM,it is considered as encountering a soft failure and the system must be stopped for maintenance or replacement.Because the degradation process is continuous,the probability that the degradation process will be in the same discrete degradation state in a certain time period is corresponding to the probability that the degradation path increment does not exceed a small value.For the discretization of the degradation process,the width of the discretization interval is determined asa=2Y/(2M-1),andXi=i·ais denoted as the degradation level of stateTherebyX(t)is supposed to be in stateiwhen the degradation level stays in the interval[lbi,ubi],wherelbiandubiare the lower and upper bounds for the degradation statei.They can be expressed as

With such a discretization,the continuous degradation process is transferred to its discrete counterpart and the number of the degradation states is finite.As an illustration,Fig.1 shows the failure mechanisms of the degrading system with the discretization of the degradation process.In Fig.1,it can be seen that the system is able to run into either the soft or the hard failure from any discrete degradation states.

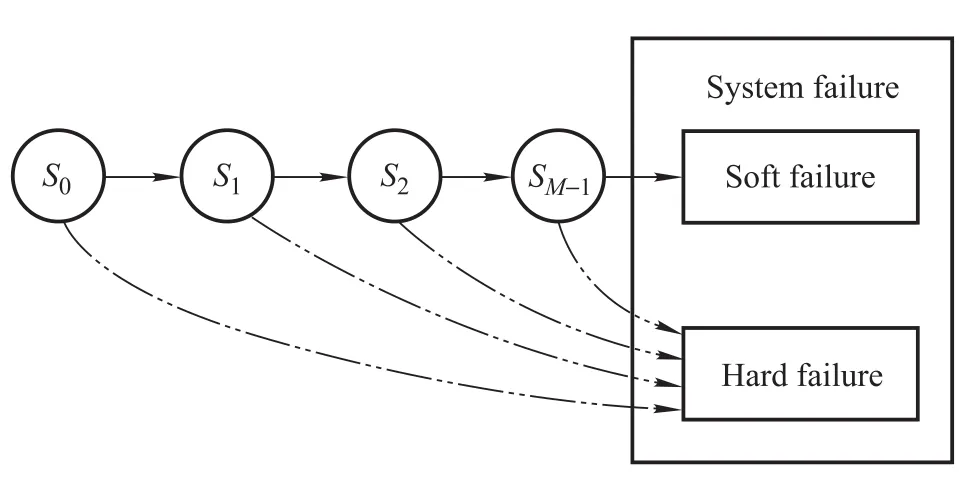
Fig.1 Failure mechanisms of the degrading system with degradation process discretization

For a critical system applied in military and space areas,there exists a maximum allowed age limitTAthat the operation time of the system is not expected to exceed due to safety matters.For the second part of the proposed discretization technique,the monitoring time axis is discretized using an equidistant time interval of lengthδ,δ＞0 and thereby the maximum allowed age limit,i.e.,the whole life cycle of the system can be represented asTA=Nδ(N≥1).In this way,all the monitoring activities and health assessment will be conducted in the confined time interval[0,Nδ].The monitoring activities can only be performed at integer multiples oftw=wδ,0≤w＜N,w∈N,and the monitoring mechanism will become more flexible whenδgoes to zero.Thus,the discrete counterpart of the transition probability(6)can be developed as

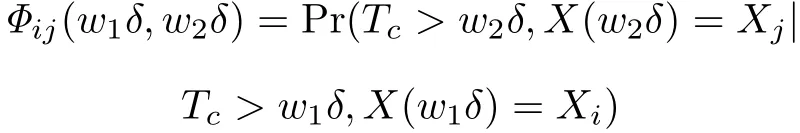
whereXi,Xjdenote the degradation levels for degradation statesi,j,respectively,0≤w1＜w2＜N.By discretizing the degradation path and the monitoring time axis,the number of the states of the joint processV(t)becomes finite,which is the key feature to enable the model evaluation.

As the fundamental element of the probability behavior of the joint process,we will focus on the transition probability behavior in a time interval of lengthδ,i.e.,the one step transition probability matrixwhose element can be obtained and derived as

It can be seen that the first part in(7)represents the probability that the joint process successfully transits from degradation stateitojduring the time interval of lengthδwithout any failure events.Considering the property of the independent increments[18,23]of the Gamma process,the increment of the degradation process in the time interval[wδ,(w+1)δ],i.e.,

Then,the first part of(7)can be written as

where 0≤i≤j≤M-1.The lower and the upper bounds are expressed as

For the second part in(7),a Cox’s PH model is applied to characterize the hazard rate of the time to hard failure.Becauseδis considerably smaller than the maximum allowed time limitTA,it is reasonable to assume that the covariate process value is constant and equal to(Xi+Xj)/2 when a transition from degradation stateitojoccurs.Thus,the element of the one-step transition probability matrix can be further obtained as(8).Using(8),the one-step transition probability matrixΦ(wδ)can be readily obtained.It should be noted,however,that due to the non-stationary behavior of the degradation process and the aging factor in the Cox’s PH model,the one step transition probability matrix is not constant and the transition elements will depend on time.To eliminate this non-stationary behavior and provide a unified framework for further model evaluation,a whole life cycle transition probability matrixPis proposed.It consists of a series ofΦ(wδ)and is organized as shown in(11),

whereeMis a unit vector ofMelements,and 0 is the zero matrix ofM×M.Denote the elemental block of the whole life cycle transition probability matrix asPw,w+1=Φ(wδ).It can be seen thatPw,w+1represents the probabilities that the joint process successfully transits from the states at time instantwδto the states at(w+1)δ.

Considering the evolution of the monitoring time,the transitions can only occur progressively with the increment ofδtime and thus other elemental blocks,for example,Pw1,w2(w2/=w1+1),will be 0.It is also worth noting that the system will not continue any longer when the operation time equals its whole life cycle timeTA=Nδ,thus,Φ((N-1)δ)=0.In this way,the system failure probability due to either the soft failure or the hard failure can be included in the last column ofP.Also,note that the whole life cycle transition probability matrix is a sparse matrix with only a series ofΦ(wδ)above its main diagonal.This appealing feature will essentially accelerate the multiplication and inversion of the matrix.In the following development,it can be seen that these are the main operations involved in the calculation of health characteristics,which are computationally efficient and can be implemented in practical applications.

Also,note that the failure probability of the system subject to dependent competing risks,i.e.,the probability that the joint process transits to either the soft failure or hard failure,is in the last column vector of the whole life cycle transition probability matrix.Thus,the probabilistic behavior of the joint processV(t)can be described by the whole life cycle transition probability matrixP.

3.Health characteristics calculation

Before proceeding to the derivation of the formulas for the health characteristics,it is necessary to analyze the structure and the properties of the matrixPin(11).Note that the last column ofPdescribes the probability that the joint process transits to either soft or hard failures from stateiattw=wδ(w=0,1,...,N-1).Thus,the whole life cycle transition probability matrixPis divided into two parts,i.e.,the degradation partBand the failure partPF,

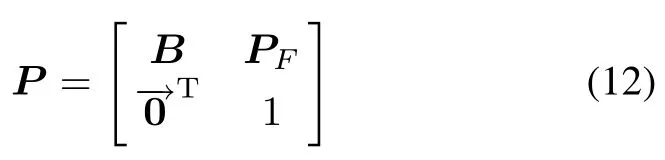
whereBis anMN×MNmatrix andis a zero vector ofMNelements.PF=(I-B)eMNis a vector ofMNelements,Iis a unit matrix andeMNis a unit vector ofMNelements.Based on this partitioned form,the related health characteristics are able to be calculated using the basic operations on the whole life cycle transition probability matrix.It should be noted that the evolution of the joint processV(t)can be presented with the multiplication of the whole life cycle matrixP.Considering the properties of the partitioned matrix,it follows immediately from(12)

Next,a new evaluation method is proposed to calculate health characteristics given the operation age and the degradation state information.The variableRLis defined as the residual life of a degrading system.From(13),it can be seen that(I-Br)eMNrepresents the probability that the degradation system will fail in the nextrδtime units,which is equivalent to the cumulative distribution ofRLgiven the degradation stateX(wδ)=Xiat the monitoring timetw=wδ.Thus,we get

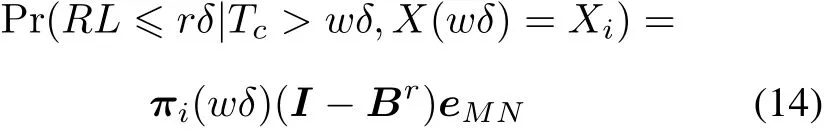
wherer= 1,2...,N-w,andπi(wδ) =(0,...,0,1,0,...,0)is the initial probability which is a 1×MNmatrix with 1 for the(wM+i)th element and zeros elsewhere,and it can be obtained given the monitoring time constanttwand the degradation statei.

Letbe the conditional probability mass function(PMF)ofRLwhich is conditioned on both the monitoring timetw=wδand the corresponding degradation statei.Based on(14),the conditional PMF ofRLcan be developed as

The residual life is a random variable and its expected value given the operation time and the corresponding degradation state,i.e.,the conditional MRL,is often applied as a point estimate for such a random variable.This health characteristic is essential to system optimization and maintenance policy making.Thus,it is appealing to derive the formula for the conditional MRL.Based on(15),the conditional MRL at monitoring timetw=wδgiven that the corresponding degradation state isican be obtained as

With the proposed transition-probability-matrix method,the health characteristics can be calculated in a feasible and unified framework.Apparently,all the formulas for the health characteristics can be obtained with the simple manipulation of the whole life cycle transition probability matrixP.WhilePis a relatively large matrix especially when the time interval of lengthδis small,however,this matrix is sparse and has non-zero block elements only along the main diagonal.

This feature essentially reduces the computational efforts such as the matrix multiplication and inversion.Thus,all the health characteristics evaluations can be obtained using a regular computational platform in an acceptable time.On the other hand,the practitioner is able to arbitrarily reduce the time interval of lengthδso as to improve the accuracy of the evaluations with a powerful computational platform.Next,a numerical study will be conducted to verify and illustrate the proposed health evaluation method.

4.Numerical study

With the degradation histories and failure information of practical engineering systems,the likelihood function can be derived and the parameters in the proposed model can be calculated using the method of maximum likelihood(MML).Considering a practical degrading system,a numerical study using assumed parameters is presented to illustrate and verify the proposed method.

For the degradation process,the shape parameter of the non-stationary Gamma process is assumed to bek(t)=0.82·t1.34,and the scale parameter is assumed to be 1.92.Without loss of generality,such a degrading system is assumed to be new without any degradation at the beginning,i.e.,X(t0)=0,t0=0.If the degradation signal surpasses the critical levelY=4,the system enters the soft failure state and thus the expendable devices connected to the system will notify users.For the discretization technique,the degradation process is discretized intoM=10 states,where state 0 is the initial state of the new or renewed system,and state 9 is the worst operation state.For the monitoring time axis discretization,the time interval of lengthδis selected as 0.1.For the baseline function of the Cox’s PH model,it is assumed to be Weibull as

where the shape parameterαand the scale parameterβare assumed to be 4.31,2.45,respectively.For illustrative purposes,the degradation processX(t)is assumed to be perfectly observable and the regression coefficientβ=0.15,and the link function is assumed to have an exponential formψ(X(t);β)=exp(0.15·X(t)).Under this assumption,the conditional MRL given the corresponding degradation state 0,i.e.,is calculated as 3.82,thus the whole life cycle of the system is reasonably selected to be more than two times ofTmean,i.e.,TA=8.00.

Considering the excellent performance of the matrix calculations,Matlab is used to implement the proposed method.To begin with,the conditional PMF ofRL,given the monitoring timet5=0.5 and the corresponding degradation state 0,can be calculated using(15)and the results are depicted in Fig.2.

Fig.2 Conditional PMF at monitoring time t=0.5 with degradation state 0

Next,the conditional RF is calculated using(16).Table 1 shows the results for the conditional RF given monitoring timet5=0.5 for several degradation states.In Fig.3,it depicts the conditional RF given the degradation statesi=0,3,6,9.As can be seen,the shape of the conditional RF is highly affected by the corresponding degradation state.This result is consistent with the observations in real applications that the competing failures are more likely to occur when the degradation level is close to the pre-defined critical level.

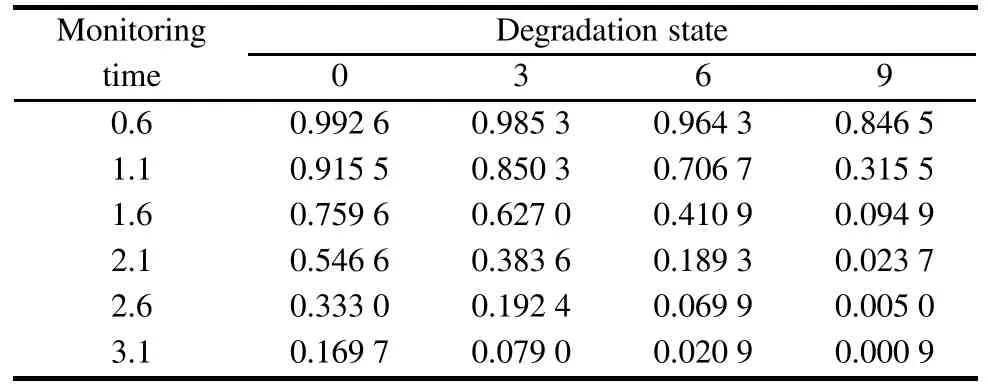
Table 1 Conditional RF at monitoring time t=0.5 given various degradation states

Fig.3 Conditional RF at monitoring time t=0.5 given various degradation states

In Fig.4,it clearly shows the conditional RF for various monitoring time,where the monitoring timet=0.1,1.6,3.1,respectively,given the monitoring state 0.As can be seen,the conditional RF gets steeper along the monitoring time axis.These trends can be attributed to the decrease of the distance between the monitoring time and the real failure time.

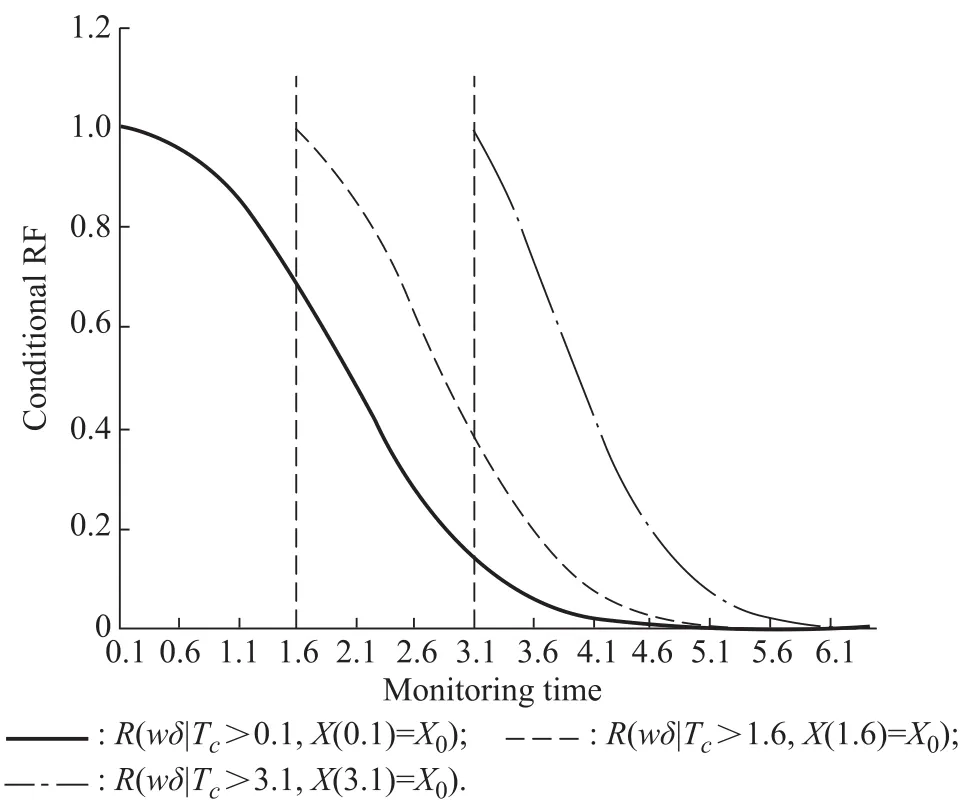
Fig.4 Conditional RF for several monitoring time instants with initial degradation state 0

To provide an illustration of the online assessment,the degradation history(t,X(t))of a practical degrading system is supposed to be(0,0),(1.5,2),(3,4),(4.5,7),(6,9).The conditional PMF of RL can be calculated by(15)and conditional MRL can be calculated by(17).Fig.5 shows the online assessment of the health characteristics when the monitoring time increases.As can be seen,the PDF gets narrower and the estimated conditional MRL is decreasing with the monitoring time increasing,which is consistent with the operations of real engineering systems.

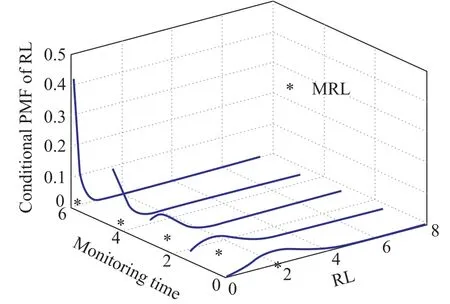
Fig.5 Online assessment of the degrading system subject to condition monitoring

In practical applications,the practitioners are interested not only in the point estimate but also in the confidence interval.Based on(15),the corresponding 95%confidence interval can be calculated.Fig.6 shows the conditional MRL and the corresponding 95%confidence interval of RL with the monitored information.As can be seen,the confidence interval gets shorter when the monitoring time increases.For instance,given that the degradation state 4 is monitored at time 3.00,the conditional MRL is calculated as 0.769 5,and the corresponding95%confidence interval is calculated as(0,1.9).

Fig.6 Conditional MRL with the corresponding 95%confidence interval

It can be seen from this numerical analysis that the health characteristics of the system subject to dependent competing risks can be feasibly evaluated with the proposed method,and the obtained explicit formulas are computationally effective for real applications.

5.Conclusions

In this paper,we propose a new health evaluation method for degrading systems subject to competing risks of dependent soft and hard failures.A non-stationary Gamma process is applied to model the system degradation.As a time-varying covariate process,this degradation process is then incorporated into the Cox’s PH model to characterize the hazard rate of the time to hard failure.Discretization techniques are applied to both the degradation path and the monitoring time axis in order to facilitate the evaluation of the characteristics of the proposed model.The explicit formulas for the health characteristics have been derived based on the proposed transition-probability-matrix method.The calculations of these health characteristics can be performed with small computational efforts and the method is applicable to obtain the online health evaluation.The procedure and the effectiveness of the proposed method have been illustrated and verified by performing a numerical study.These illustrative results have shown that our method is able to be implemented effectively for a degrading system subject to condition monitoring so as to provide a basis for the optimal maintenance policy making and to prevent the possible catastrophic failures and their consequences.

[1]SI X,WANGW,HUC,et al.Remaining useful life estimation:a review on the statistical data driven approaches.European Journal of Operational Research,2011,213(1):1–14.

[2]PECHT M,JAAI R.A prognostics and health management road map for information and electronics-rich systems.Microelectronics Reliability,2010,50(3):317–323.

[3]ZHOU Q,SON J,ZHOU S Y,et al.Remaining useful life prediction of individual units subject to hard failure.IIE Transactions,2014,46(10):1017–1030.

[4]MA Z,KRINGS A W.Competing risks analysis of reliability,survivability,and prognostics and health management(PHM).Proc.of IEEE Conference on Aerospace,2008:1–21.

[5]ZHAO W,ELSAYED E A.An accelerated life testing model involving performance degradation.Proc.of Annual Symposium on Reliability and Maintainability,2004:324–329.

[6]BOCCHETTI D,GIORGIO M,GUIDA M,et al.A competing risk model for the reliability of cylinder liners in marine Diesel engines.Reliability Engineering&System Safety,2009,94(8):1299–1307.

[7]GUO C,WANG X,GUO B.Competing risk model for long-stop-short-run systems.Proc.of Prognostics and System Health Management Conference,2011:1–7.

[8]WANG H,GAO J.A reliability evaluation study based on competing failures for aircraft engines.Eksploatacja i Niezawodnosc-Maintenance and Reliability,2014,16(2):171–178.

[9]TANG D,YU J.Optimal replacement policy for a periodically inspected system subject tothe competing soft and sudden failures.Eksploatacja i Niezawodnosc-Maintenance and Reliability,2015,17(2):228–235.

[10]KHALEGHEI A,MAKIS V.Reliability estimation of a system subject to condition monitoring with two dependent failure modes.IIE Transactions,2016,48(11):1058–1071.

[11]GUO C,WANG W,GUO B,et al.Maintenance optimization for systems with dependent competing risks using a copula function.Eksploatacja i Niezawodnosc-Maintenance and Reliability,2013,15(1):9–17.

[12]HUYNH K T,BARROS A,BRENGUER C,et al.A periodic inspection and replacement policy for systems subject to competing failure modes due to degradation and traumatic events.Reliability Engineering&System Safety,2011,96(4):497–508.

[13]RAFIEE K,FENG Q,COIT D W.Reliability modeling for dependent competing failure processes with changing degradation rate.IIE Transactions,2014,46(5SI):483–496.

[14]SONG S,COIT D W,FENG Q.Reliability analysis of multiple-component series systems subject to hard and soft failures with dependent shock effects.IIE Transactions,2016,48(8):720–735.

[15]SANTINI T,MORAND S,FOULADIRAD M,et al.Accelerated degradation data of SiC MOSFETs for lifetime and remaining useful life assessment.Microelectronics Reliability,2014,54(9/10):1718–1723.

[16]ZHAO S,MAKIS V,CHEN S,et al.Reliability evaluation for an electronic system subject to competing risks of dependent soft and hard failures.Proc.of Prognostics and System Health Management Conference,2016:1–7.

[17]VICHARE N M,PECHT M G.Prognostics and health management of electronics.IEEE Trans.on Components and Packaging Technologies,2006,29(1):222–229.

[18]VAN NOORTWIJK J M.A survey of the application of gamma processes in maintenance.Reliability Engineering&System Safety,2009,94(1):2–21.

[19]BANJEVIC D.Calculation of reliability function and remaining useful life for a Markov failure time process.IMA Journal of Management Mathematics,2006,17(2):115–130.

[20]BROOK D,EVANS D A.An approach to the probability distribution of CUSUM run length.Biometrika,1972,59(3):539–549.

[21]ZHAO S,MAKIS V,CHEN S,et al.On-line reliability assessment for an electronic system subject to condition monitoring.Proc.of IEEE International Conference on Prognostics and Health Management,2016:1–6.

[22]FU J C,SPIRING F A,XIE H.On the average run lengths of quality control schemes using a Markov chain approach.Statistics&Probability Letters,2002,56(4):369–380.

[23]SON K L,FOULADIRAD M,BARROS A.Remaining useful lifetime estimation and noisy gamma deterioration process.Reliability Engineering&System Safety,2016,149:76–87.