Differential game strategy in three-player evasion and pursuit scenarios

SUN Qilong,QI Naiming,*,XIAO Longxu,and LIN Haiqi

1.Department of Aerospace Engineering,Harbin Institute of Technology,Harbin 150001,China;2.The Rocket Force Equipment Academy,Beijing 100096,China

1.Introduction

In an aerial scenario,it is difficult for a missile to attack an aircraft,because the aircraft always launches a defender against the missile.Thus,it is necessary to develop a feasible guidance law for a missile to attack an aircraft. The scenario involves three agents,namely an aircraft(target),an attacking missile(attacker),and a defending missile(defender).

The one-on-one engagement has been investigated for a long time and several guidance laws have been presented[1–3].In recent years,various pursuit-evasion scenarios involving multiple agents have been developed.A scenario in which two players pursuing a target was described in[4–6].In those studies,the authors always solved the problem using a differential theory.In contrast to two attackers pursuing one target,Xiao et al.[7]presented a cooperative guidance law for a multimissile system in which the missiles cooperated with each other to attack the target.References[8,9]described a scenario where one attacker pursued two targets.In the scenario,the two evaders cooperated with each other to evade the pursuer.An active defense system has been more popular recently.Boyell and Shinar[10–12]described a scenario in which a defender and a fixed or slowly moving target constituted the defended system,which used a derived optimal guidance law against the missile.In that study,the authors always assumed that the position and the trajectory of the target were known to the defender,and that the position and the motion state of the attacker were also known to the defender.Rusnak[13,14]presented a differential game for three persons:a lady,a bandit,and a bodyguard.The bandit pursued the lady and the lady tried to evade the bandit;meanwhile,the bodyguard minimized the distance from the bandit to protect the lady.The problem was solved by using a differential theory of multiple players.Later,Rusnak[15]investigated a high-order participant for an active defense system.Ratnoo and Shima[16]proposed an approach to protect the target;the defender used the line-of-sight guidance law to pursue the attacker.References[17,18]presented an optimal cooperative guidance law for a target and a defender against an attacking missile using differential and linear quadratic theories,respectively.The authors considered the target and the defender as a cooperative system,and they assisted each other to win the game.Shima and Ratnoo[19]analyzed a three-player problem in which an attacker and a defender used different guidance laws;they analyzed the conditions for the attacker to win the game.Later,Rubinsky and Gut-man[20,21]presented a three-player scenario in which a missile evaded a defender and continued to pursue the target.In this scenario,the target and defender were independent.Garcia et al.[22–24]presented a defended system that contains a target and a defender.The target and the defender send information to each other and seek an optimal cooperative strategy against the homing missile.They investigated the guidance law by using nonlinear dynamics.Kumar and Shima[25]derived an optimal cooperative guidance law by using nonlineardynamics,assuming that the attacking missile used a linear proportional guidance law.Particularly,in that study,they used a zero-effort velocity to ensure zero terminal relative lateral velocity,and doing so reduced the sensitivity of the guidance law to erroneous time-to-go estimates.

In this study,we derive the optimal guidance laws for the attacker to intercept the target assuming that the defender and the target use the optimal one-to-one guidance laws.This study also chooses the miss distance as the outcome of the conflict;however,it is different from the guidance law presented by Rubinsky and Gutman.For some cases,the attacker can accomplish the attacking task by using the one-to-one optimal guidance law provided that a reasonable pursuit acceleration within the maximal acceleration for the attacker is chosen.Using the optimal one-to one guidance law damages the collision triangle slightly and the acceleration of the attacker does not have to be much greater than the target;thus,as shown in[22],it is not necessary to evade the defender first.For some situations,it is difficult to accomplish the task if the attacker is only assigned to a pursuit acceleration within the maximal acceleration.Thus,we derive a guidance law for the attacker to evade the defender to a critical safe value,and to guarantee that the zero-effort-miss(ZEM)distance between the attacker and the target is the smallest.Then the attacker uses the optimal one-to-one guidance law to accomplish the task.

2.Problem formulation

2.1 Nonlinear dynamics

The problem consists of three players:an attacker(A),a target(T)and a defender(D).It is assumed that the defender is launched from the target to intercept the attacker.In the problem,the target and the defender’s positions,velocities,and accelerations are known to the attacker.The endgame scenario is described in Fig.1.The range between the players is defined by R; the velocity of the player is defined by V;the flight path angle is denoted by γ;the line of sight is denoted by LOS;λ presents the angle between line of sight and the X axis,and a the lateral acceleration of the player.The subscripts A,T,and D correspond to the attacker,the target and the defender.The subscripts AT and AD present the corresponding parameters between the attacker and the target,and the attacker and the defender,respectively.

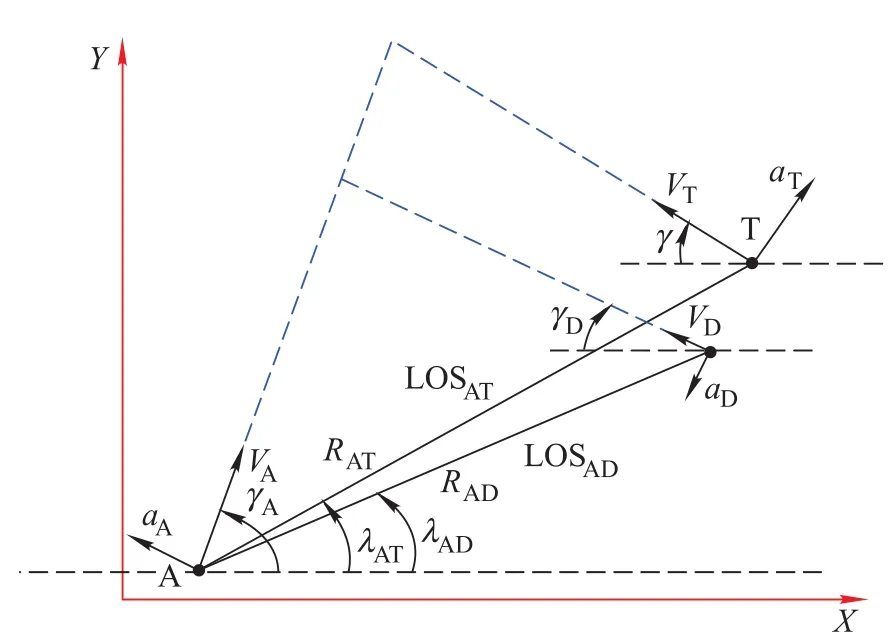
Fig.1 Engagement geometry

The range rate is given by

2.2 Linearized kinematics

It is assumed that the problem occurs in the endgame phase and the flight near the collision triangle can be linearized around LOS0.The subscript 0 represents the initial state.The relative displacement between A and T normal to LOSAT0is denoted as yATand the relative displacement between A and D normal to LOSAD0is denoted as yAD.The accelerations of A and T normal to LOSAT0and the acceleration of D normal to LOSAD0are denoted byuiL{i=A,T,D},and they satisfy

whereuA,uT,anduDare the controllers normal to the corresponding LOS and they satisfy the following form:

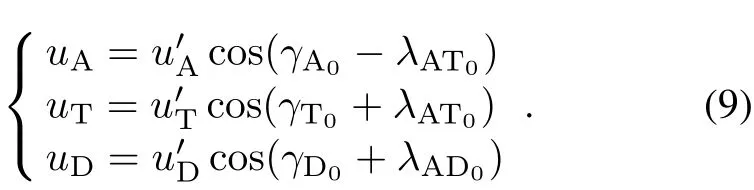
The state vector of the linearized engagement is expressed as follows:

where the dimension ofxis 4+nA+nT+nD.

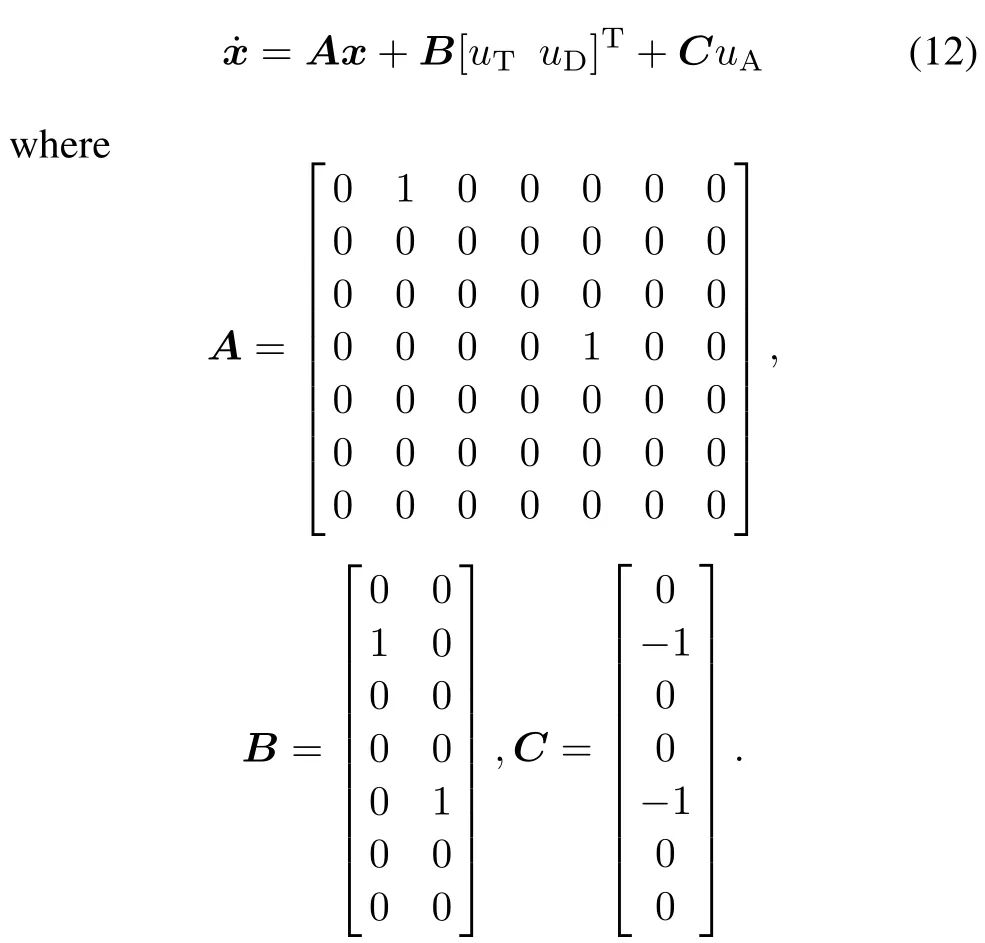
It is assumed that A,T and D obey ideal dynamics,and LOSAT0and LOSAD0are coincident.The equations of motion corresponding to(10)are given by

The equations can be written in the following form:

By linearizing the kinematics around the collision triangles,the intercept times are considered to be fixed and can be given by

whereRAT0andRAD0are the initial ranges between A and T,and between A and D,respectively.andare the initial relative velocities.In order to defend the target,the defender must intercept the attacker prior to the intercept time between the attacker and the target.It is considered that after,the defender will disappear.We define a new parameterin the following form:

whereis the time-to-go of A and T,andis the time-to-go of A and D.

3.Differential game description

3.1 Order reduction

The ZEM distance between the attacker and the target can be obtained by using(15)below.

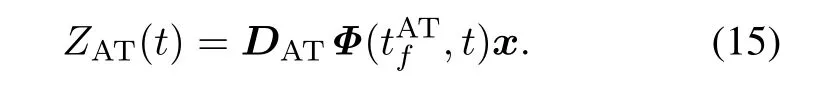
Similarly,the ZEM distance between the attacker and the defender can be obtained by

whereare the transition matrices corresponding to(12)and they are expressed as

whereIrepresents the identity matrix.

DADandDATare given by

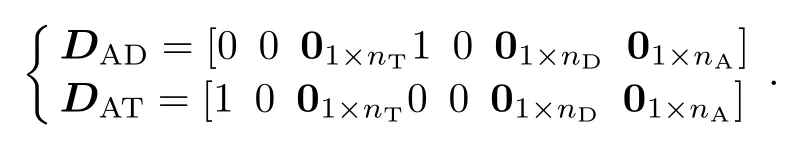
Equations(15)and(16)can be rewritten in the following form:

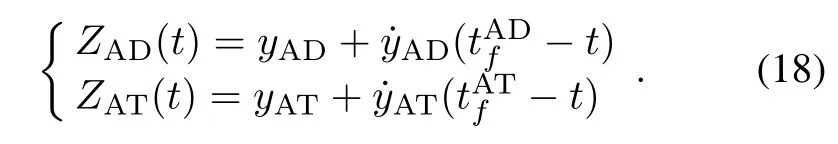
In order to find the dynamics ofZAT(t)andZAD(t),we differentiate them with respect to time and combine them with(17).Their dynamics are given as

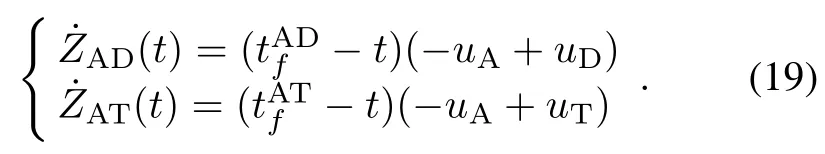
The optimal guidance law corresponding to(15)can be obtained as follows:

The optimal guidance law corresponding to(16)can be obtained as follows:

3.2 Optimal evasion trajectories for attacker

We investigate the optimal trajectories for A to evade from D.It is assumed thatis given by

It is assumed that the kill radius of the defender is smaller thanR;thus,ifthe defender cannot intercept the attacker.Defining,we can obtain the two border trajectories in the following form:

The optimal trajectories are shown in Fig.2,and the two border trajectories are described with thicker lines.

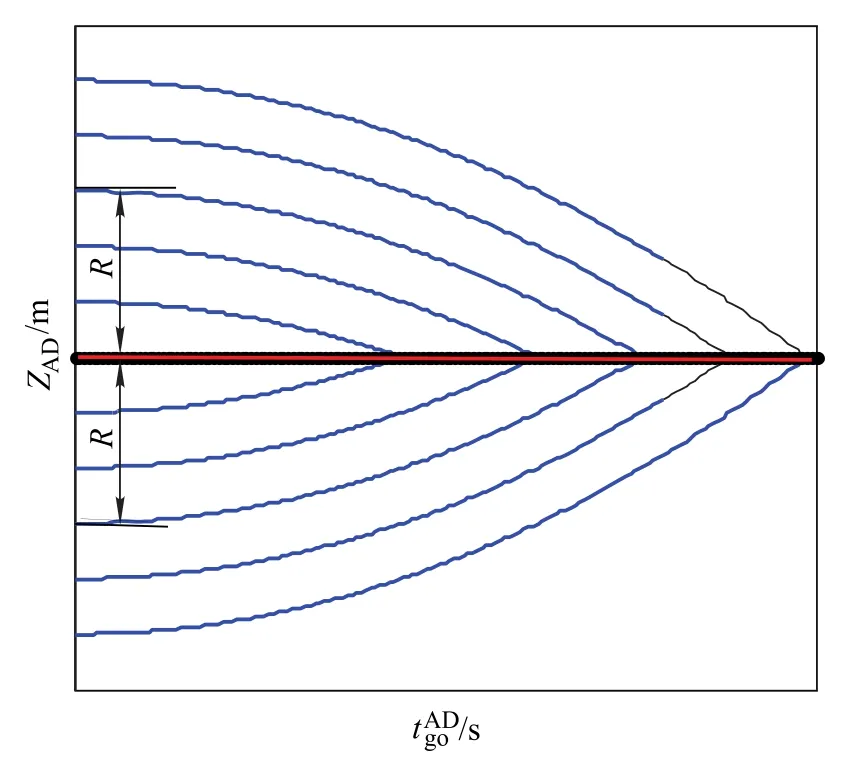
Fig.2 Optimal trajectories of ZAD

In the engagement,A and D use the optimal strategy;if

ZADis located within the zone between the two border trajectories,the attacker will be intercepted by the defender.Conversely,ifZADis located outside the zone between the two border trajectories,the attacker will win the game.

3.3 Optimal pursuit trajectories for attacker

We then solve for the optimal trajectories for A to pursue T.It is assumed thatis given by

It is assumed that the kill radius of the attacker isR1;thus,ifthe attacker can accomplish the attacking task.The two border trajectories are obtained by defining

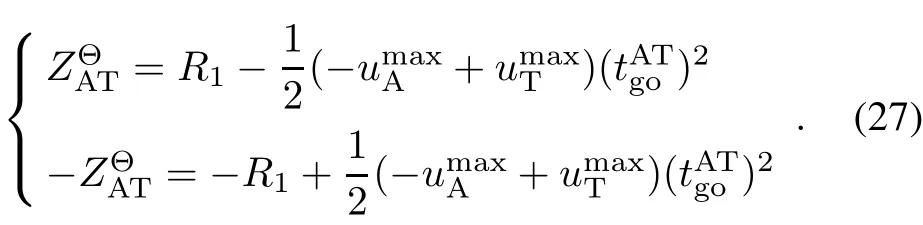
Fig.3 shows the optimal trajectories,and the two border trajectories are described with thick lines.In the engagement the attacker uses the optimal pursuit strategy and the target uses the optimal evasion strategy.IfZATis located within the zone between the two border trajectories,the attacker can intercept the target.Conversely,ifZATis located outside the zone between the two border trajectories,the target can evade the attacker.The maximum permittedfor the attacker to win the game is given by

If the attacker wants to win the game,should not be greater than a value defined bywherecan be obtained from(29).

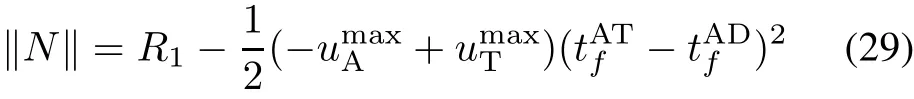
Fig.3 Optimal trajectories of ZAT

4.Guidance law of the attacker

In order for the attacker to win the game,we need to analyze the required conditions for the attacker to accomplish the evasion and pursuit task and then design a feasible guidance law for the attacker.We divide the engagement into two cases.

4.1 Case 1:the signs of ZAT(t=0)and ZAD(t=0)are opposite

In this case,we can obtain-signZAD(t)=signZAT(t);thus,the optimal evasion and pursuit control efforts for the attacker are the same and the attacker can accomplish the optimal evasion and pursuit action simultaneously in the engagement.Fig.4 shows the time evolution of ZEM distance for Case 1.In this figure,ZADrepresents the ZEM between the defender and the attacker for Case 1 as a function of time.ZATrepresents the time evolution of ZEM between the target and the attacker.The meanings of the two lines are the same for the subsequent figures.

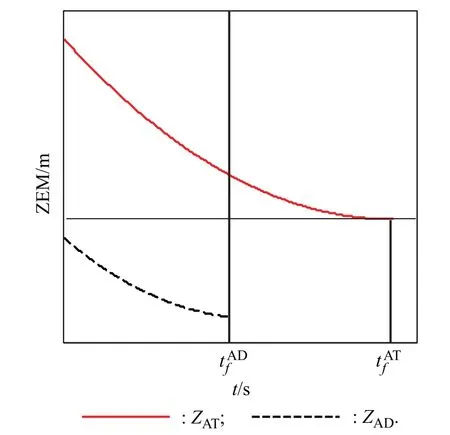
Fig.4 ZEM distance for case 1 as a function of time

4.2 Case 2:the signs of ZAT(t=0)and ZAD(t=0)are the same

In this case,we can obtain signZAD(t)=signZAT(t);thus,the attacker’s optimal guidance law of(20)is contrary to the optimal guidance law of(21),which means that if the attacker uses the optimal pursuit guidance law to pursue the target,it will simultaneously perform the worst in evading the defender.Fig.5 shows the ZEM distance for Case 2 as a function of time.We only analyze the positive values ofZAT(t=0)andZAD(t=0),because the analysis is the same for negative values.

Fig.5 ZEM distance for case 2 as a function of time

When the attacker only uses the optimal pursuit guidance law to intercept the target,the required conditions for the attacker to avoid the defender can be divided into two cases.The first required condition is thatZAD(t=0)is a relatively large positive value.The schematic figure for the first condition is shown in Fig.6.In the figure,is the border trajectory above the zero axis.It is noted that=Ris a critical value.For this case,satisfies the following form:

IfZAD(t= 0)≥R+the attacker can avoid the defender.Combining(28)and(31),we can obtain the initial conditions ofZAD(t=0)andZAT(t=0)for the attacker to accom-plish the task,and these conditions are in the following form:

Fig.6 ZEM distance for the first condition as a function of time

The second required condition is thatZAD(t=0)is a relatively small positive value.The schematic figure for the second condition is shown in Fig.7.Here,is the border trajectory below the zero axis.It is noted thais a critical value.For this casesatisfies the following form:

Similarly,it is assumed that whenthe criticalZAD(t=0)can be obtained by

the attacker can avoid the defender.Under the condition thatby combining(36)and(28),we obtain the initial conditions ofZAD(t=0)andZAT(t=0)for the attacker to accomplish the task,and the conditions are in the following form:

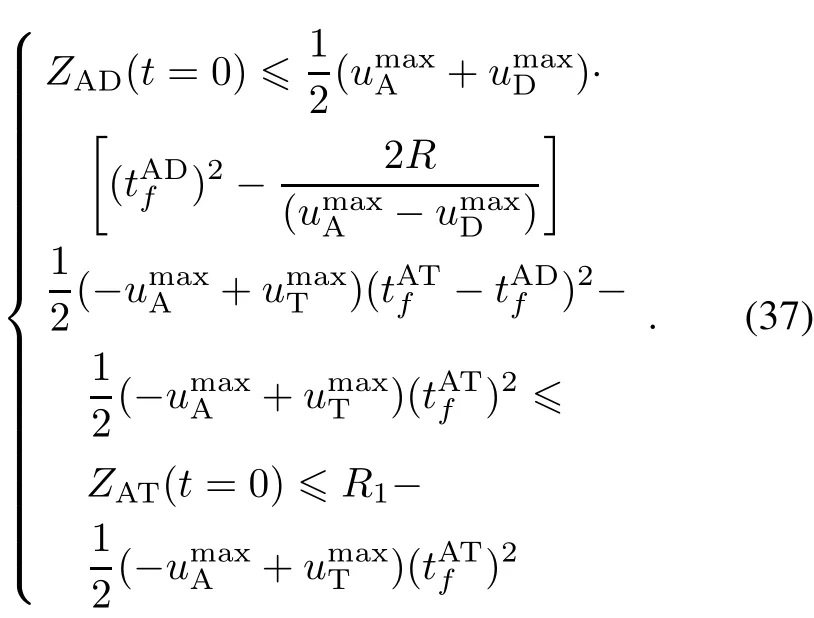
Fig.7 ZEM distance for the second condition as a function of time

IfZAD(t=0)is not a relatively large positive value or a relatively small positive value,for the attacker to accomplish the attacking task,we need to design a guidance that guarantees the evasion and pursuit distance,which areWe only analyze the positive values ofZAT(t=0)andZAD(t=0).It is assumed that during the final timethe attacker employs a consistent control effort defined byuA.By definingand substitutinguAinto(19)and integrating it,we obtain

Thus,the control range for the attacker to evade the defender is obtained by

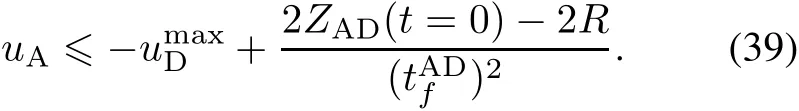
SubstitutinguAinto(19)and integrating it,we obtain

It is noted thatis a monotonically decreasing function ofuA.Within the control range for the attacker to evade the defender,the largest value of the attacker’s acceleration satisfies

Thus,is a border value that can guaranteeis the smallest value within the permitted control range for the attacker to reach the safe area atThus,during the final timewe selectas the control effort of the attacker;afterthe attacker uses the optimal guidance law of(21)to accomplish the pursuit task.

It is known that for the attacker to accomplish the task,based on(29),should satisfy(42).

Thus,combining(44)andZAT(t=0)≥0,we can obtain the permitted range forZAT(t=0)in the following form:

It is known that if we use the derived guidance law,and ifZAT(t=0)satisfies(45),the attacker can accomplish the evasion and pursuit task.The derived guidance law has the following form:

Fig.8 shows the ZEM distance for the derived guidance law as a function of time.It is noted that the attacker uses the designed guidance law to ensure that the ZEM distance between the attacker and the defender reaches the bounded valueand to guarantee thatis the smallest value.Afterthe at tacker uses the optimal one-to-one guidance law as outlined in(21)to accomplish the pursuit task.

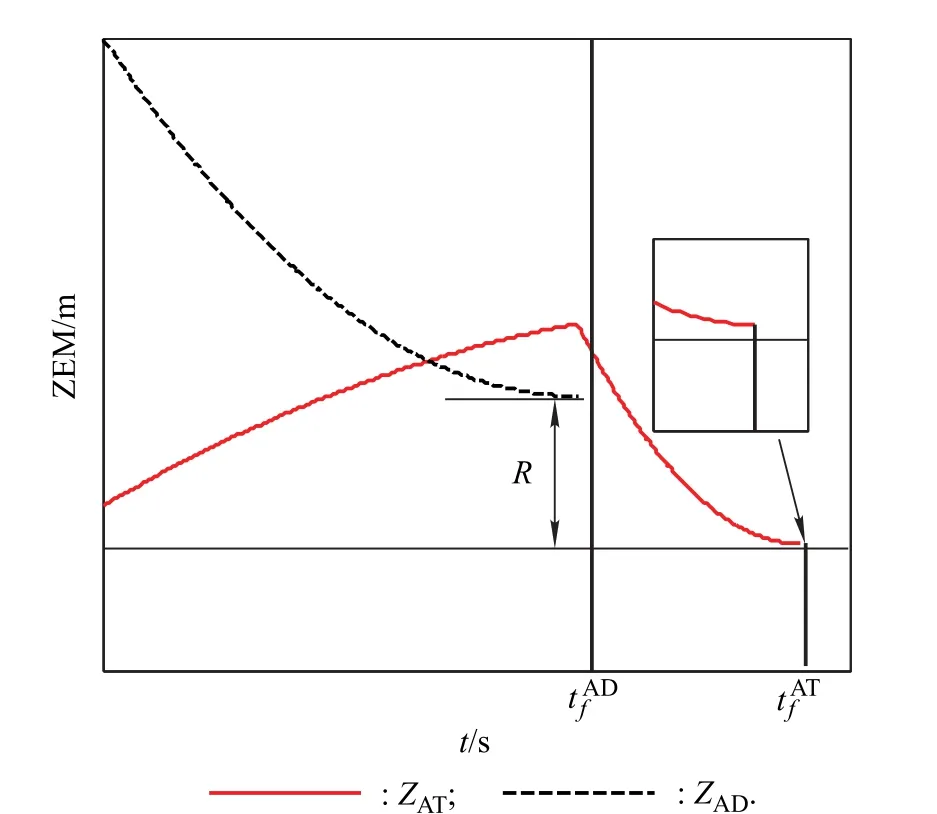
Fig.8 ZEM distance for the derived guidance law as a function of time

5.Simulation

In this section,the different guidance laws are verified and the required conditions are analyzed.The initial parameters are given in Table 1.RandR1are assumed to be 80 m and 2 m,respectively.

Table 1 Initial parameters

5.1 Simulation of Case 1

The initial conditions are given in Table 2.The initialZAT(t=0)andZAD(t=0)are 609.707 m and–53.909 m,respectively.

Table 2 Initial parameters for Case 1

For this case,if the attacker pursues the target by using the one-to-one optimal guidance law,it can simultaneously evade the defender.

We use nonlinear simulation to analyze this situation.Fig.9 shows the trajectories of the three players.It is noted that the miss distance between the attacker and the target,and the miss distance between the attacker and the defender are 0.428 m and 89.705 m,respectively.Thus,the attacker can avoid the defender and intercept the target.The final time,,are 6.595 2 s and 3.948 5 s,respectively.

Fig.9 Trajectories with parameters shown in Table 2

Fig.10shows the time evolution of the time-to-go.It can be observed thatis almost linear in form;however,atthere exists a turning point whereZATis a very small value close to zero.After the turning point,the accelerations of the attacker and the target display the bang-bang phenomenon.Fig.11 shows the trajectories of the three players when the maximal acceleration of the defender becomes 80 m/s2.Here,the miss distance between the attacker and the defender decreases to 50.125 m and the attacker is intercepted.For this case,if the attacker wants to accomplish the task, it must have a greater maximal acceleration.It is assumed that the attacker’s maximal acceleration becomes 100 m/s2.Thus,the maximal accelerations of the attacker and the defender are 100 m/s2and 80 m/s2,respectively.Fig.12 and Fig.13 show the trajectories of the three players and the time evolution of the time-to-go,respectively.

Fig.10 Time-to-go with parameters shown in Table 2

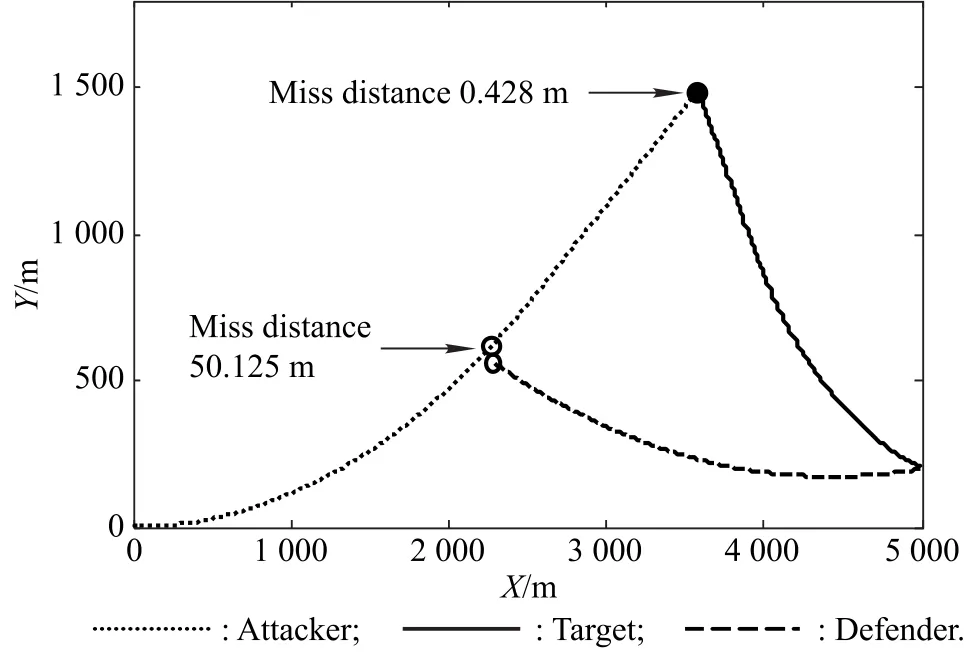
Fig.11 Trajectories with parameters shown in Table 2 except

Fig.12 Trajectories with parameters shown in Table 2 except

Fig.13 Time-to-go with parameters shown in Table 2 except

It can be noted that the miss distance between the attacker and the target and that between the attacker and the defender are 0.126 m and 101.765 m,respectively;thus,the attacker can intercept the target.The final time,and,are 3.962 3 s and 6.162 5 s,respectively.Because the maximal acceleration of the attacker increases, the miss distance between the target and the attacker decreases to a smaller value than that shown in Fig.9,and the turning point occurs earlier than that shown in Fig.10.

5.2 Simulation of Case 2

Example 1 The initial conditions are given in Table 3.The initialZAT(t=0)andZAD(t=0)are609.707mand 1 311.582m,respectively.ZAD(t=0)is a relatively large value for this situation.The attacker can only use the one to-one optimal guidance law to pursue the target.Although this case is rare,it does exist and needs to be analyzed.

Table 3 Initial parameters for Example 1

For this case,if the attacker pursues the target by using the one-to-one optimal guidance law,it makes the worst maneuver to evade the defender.Similar to the previous case,we analyze this situation by using nonlinear simulation.Fig.14 and Fig.15 show the trajectories of the three players and the time evolution of the time-to-go.The miss distance between the attacker and the target,and the final timeare still 0.428 m and 6.595 2 s,respectively.The miss distance between the attacker and the defender is 101.156 m,and the attacker can accomplish the task.The final timeis 3.991 2 s.Fig.16 shows the trajectories of the three players when the maximal acceleration of the defender is assigned to a greater value,such as 80 m/s2.Here,the miss distance between the attacker and the defender decreases to 56.143m and the attacker cannot accomplish the task.For this case,if the attacker wants to intercept the target,it must have a smaller maximal acceleration.It is assumed that the maximal accelerations of the attacker and the defender become 73 m/s2and 80 m/s2,respectively.Fig.17 and Fig.18 show the trajectories of the three players and the time evolution of the time-to-go.

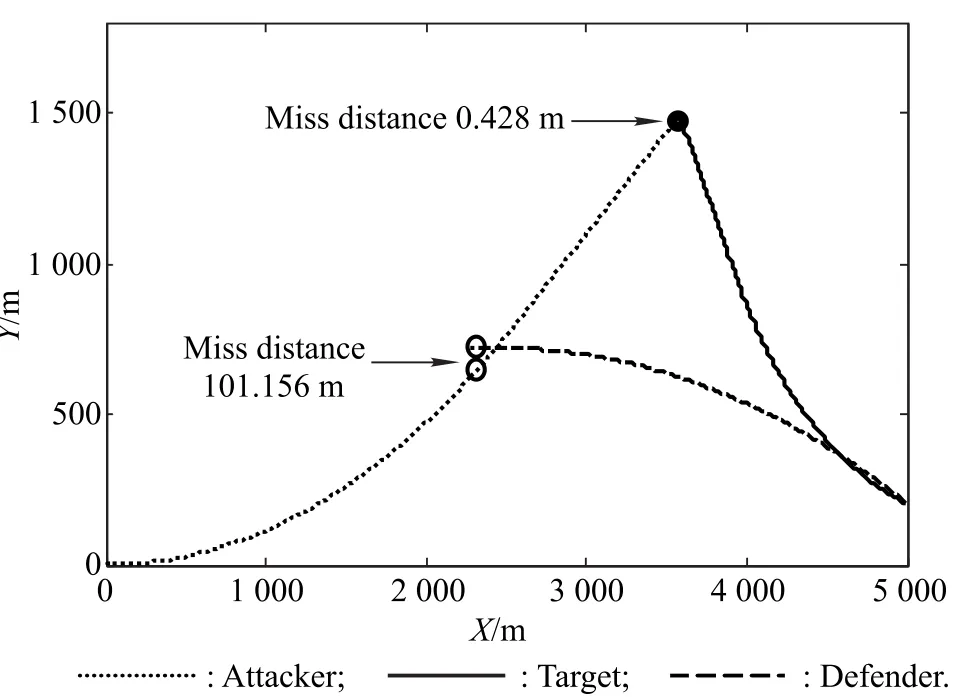
Fig.14 Trajectories with parameters shown in Table 3

Fig.15 Time-to-go with parameters shown in Table 3

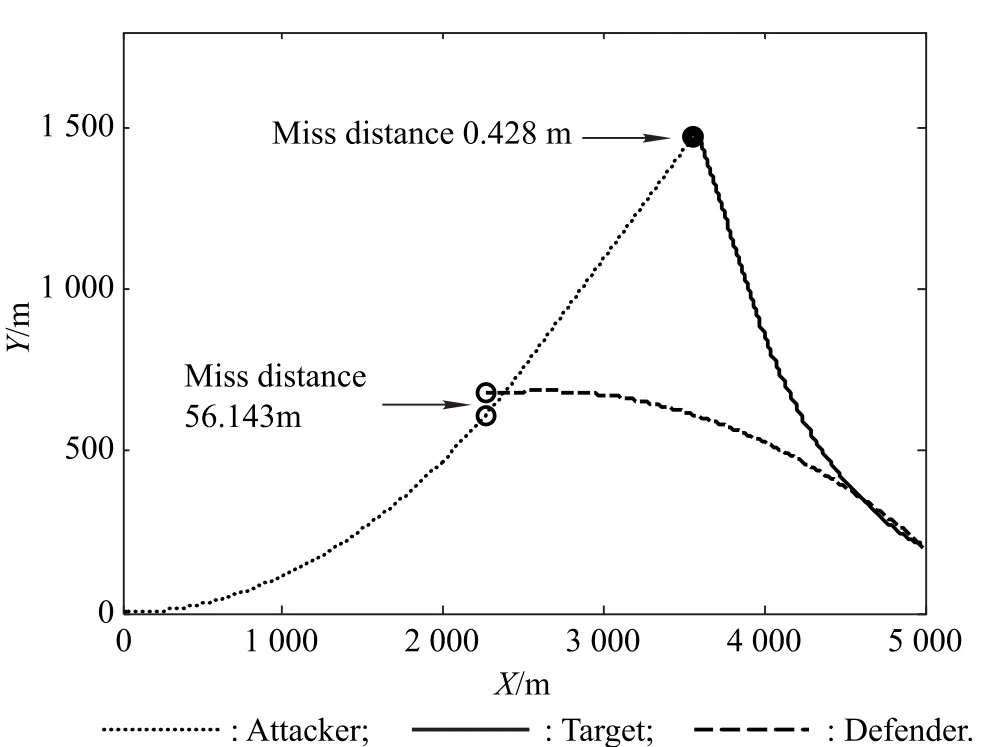
Fig.16 Trajectories with parameters shown in Table 3 except

Fig.17 Trajectories with parameters shown in Table 3 except

Fig.18 Time-to-go with parameters shown in Table 3 except

It is observed that the miss distance between the attacker and the target and that between the attacker and the defender are 0.728 m and 120.146 m,respectively;thus,the attacker can accomplish the task.The final timeandare 3.969 8 s and 6.867 5 s,respectively.As the maximal acceleration of the attacker becomes smaller,the miss distance between the target and the attacker rises to a greater value than that shown in Fig.14 and the turning point occurs later than that shown in Fig.15.

Example 2The initial conditions are given in Table 4.The initialZAT(t=0)andZAD(t=0)are 609.707 m and 578.876 m,respectively.ZAD(t=0)is a relatively small value for this situation.The attacker can only use the one-to-one optimal guidance law to pursue the target.This case is common;thus,it is important to analyze it.

Table 4 Initial parameters for Example 2

We also analyze this situation by using nonlinear simulation.The miss distance between the attacker and the target,and the final timeare still 0.428 m and 6.595 2 s,respectively,which are shown in Fig.19 and Fig.20,respectively.The miss distance between the attacker and the defender is 89.761 m,and the final timeis 3.921 5 s.It is assumed that the maximal acceleration of the defender is assigned to a greater value,such as 65 m/s2.

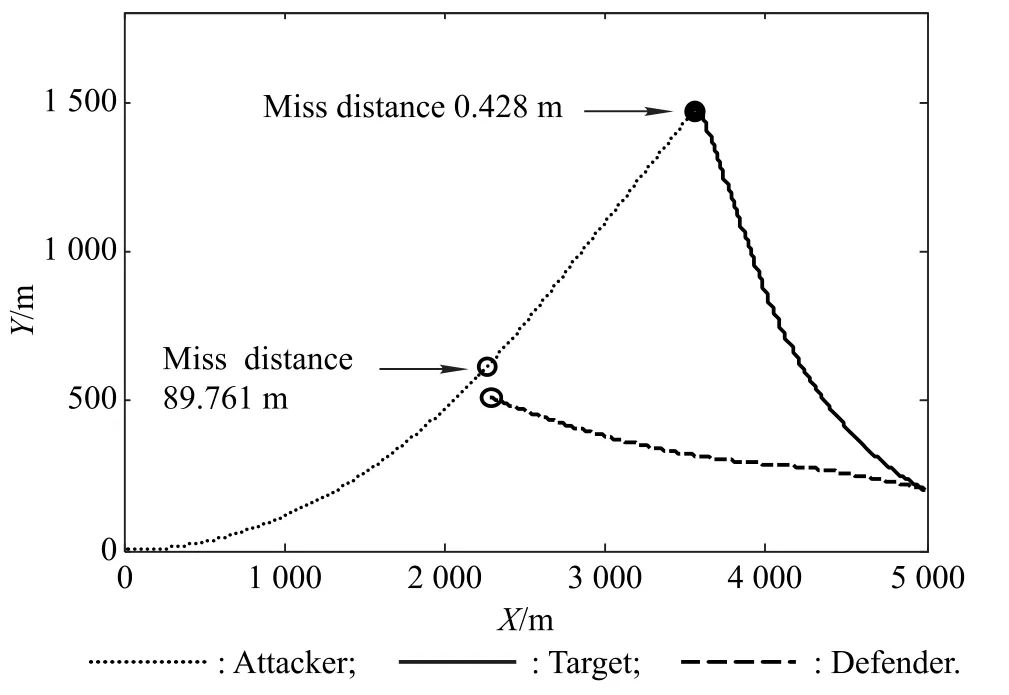
Fig.19 Trajectories with parameters shown in Table 4

Fig.20 Time-to-go with parameters shown in Table 4

The trajectories of the three players are shown in Fig.21,in which the attacker is intercepted by the defender.Through Fig.7 we can conclude that if we want to increase the miss distance between the attacker and the defender,we can assign a greater value to the maximal acceleration of the attacker.It is assumed that the maximal accelerations of the defender and the attacker are 65 m/s2and 100 m/s2,respectively,and the trajectories for this situation are shown in Fig.22.It can be noted that although the attacker’s maximal acceleration increases,the miss distance between the attacker and the defender cannot increase;this is because the attacker uses the optimal one-to-one guidance law to pursue the target,and the acceleration is restricted byZAT.When the attacker’s maximal acceleration becomes greater,ZATreduces to zero more quickly,and the bang-bang phenomenon occurs earlier.From Fig.7,it can be concluded that by increasingZAT(t=0),we can obtain a greater miss distance between the attacker and the defender.The attacker’s initial course is redefined by – 2°and the initialZAT(t=0)andZAD(t=0)are 728.585 m and 660.707m,respectively.The maximal accelerations of the defender and the target are still 65 m/s2and 100 m/s2,respectively,and the nonlinear simulation results are shown in Fig.23 and Fig.24.For this case,it is observed that the miss distance between the attacker and the target,and that between the attacker and the defender are 0.153m and 90.418m,respectively;thus,the attacker can intercept the target.The final timeare 3.961 1 s and 6.317 5 s,respectively.As the maximal acceleration of the attacker becomes greater,the miss distance between the target and the attacker decreases to a smaller value than that shown in Fig.19 and the turning point occurs earlier than that shown in Fig.20.

Fig.21 Trajectories with parameters shown in Table 4 except

Fig.22 Trajectories with parameters shown in Table 4 except

Fig.23 Trajectories with parameters shown in Table 4 except

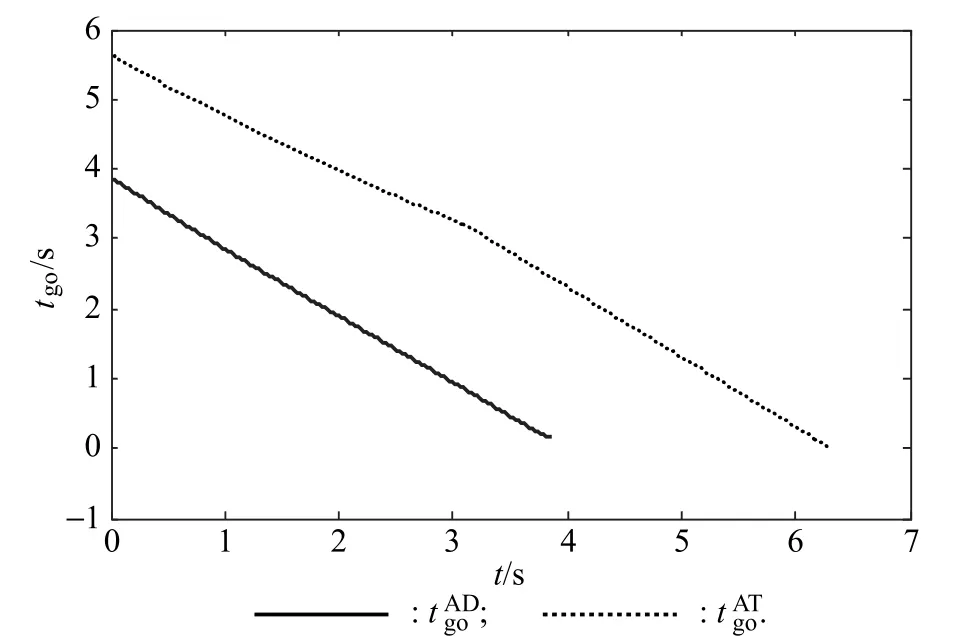
Fig.24 Time-to-go with parameters shown in Table 4 except

Example 3The initial conditions are given in Table 5.The attacker uses the guidance law corresponding to(46),which is similarly tested by using nonlinear simulation.

Table 5 Initial parameters for Example 3

Fig.25 and Fig.26 show the trajectories and time-to-go by using the parameters given in Table 5.The miss distance between the attacker and the defender is 80.704 m,and the miss distance between the attacker and the target is 0.319 m;thus the attacker wins the game.The final timesare 15.633 1 s and 6.510 5 s,respectively.It can be noted that the time evolution ofis not linear in form but finally becomes approximately linear with a decreasing slope.This is because when using this guidance law,the attacker needs to avoid the defender first and damages the collision triangle heavily;however,a new collision triangle is established during the final attacking period.Fig.27 shows the trajectories for the case where the maximal acceleration of the defender changes to 100 m/s2and the other parameters remain the same.

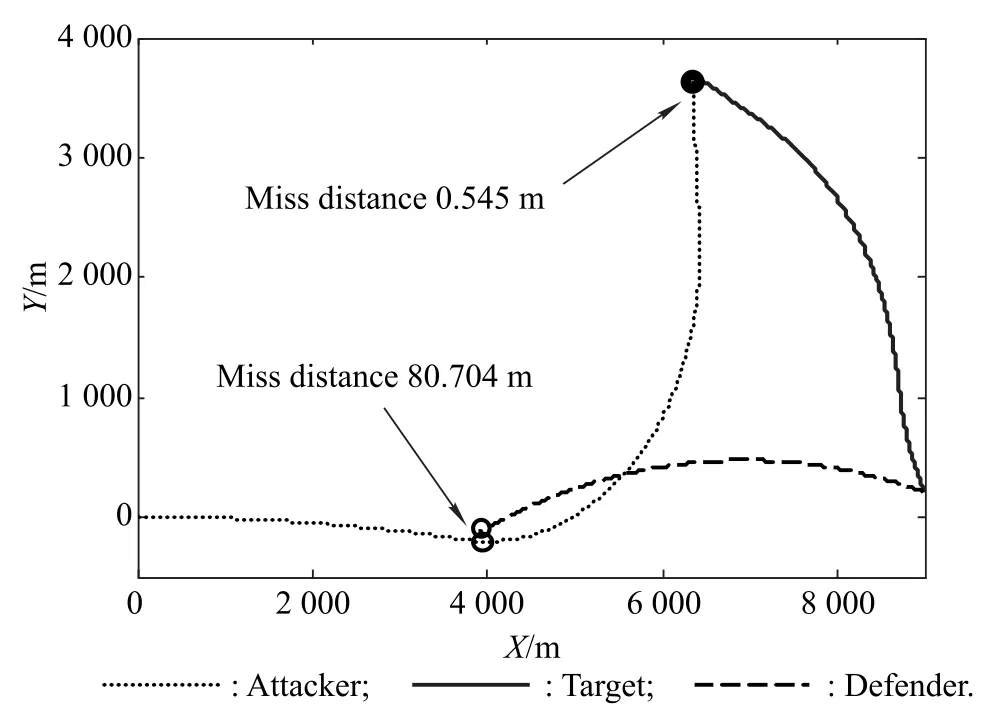
Fig.25 Trajectories with parameters shown in Table 5

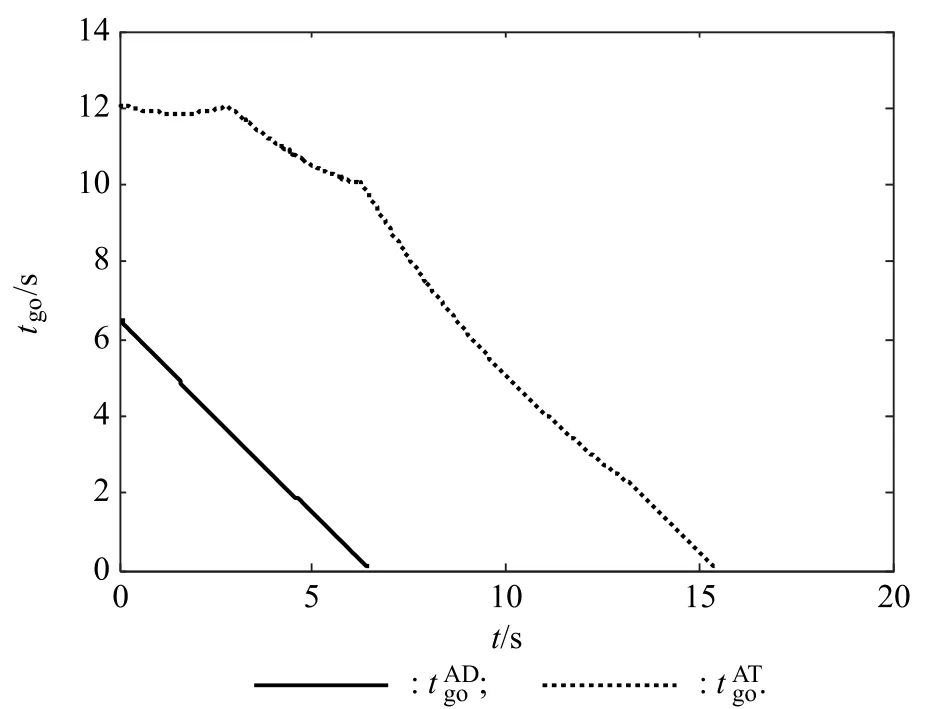
Fig.26 Time-to-go with parameters shown in Table 5

Fig.27 Trajectories with parameters shown in Table 5 except

As can be observed,the attacker fails to complete this task.In order to accomplish the task,the attacker’s maximal acceleration must be greater than 150 m/s2.It is assumed that the maximal accelerations of the defender and the attacker are 100 m/s2and 180 m/s2,while the other parameters are invariant.The new trajectories and time to-go are shown in Fig.28 and Fig.29.The miss distances are 80.236m and0.429m,respectively;thus,the attacker wins.The final timeare 16.3741 s and 6.635 2 s,respectively.It can be noted that using this guidance law,the attacker’s maximal acceleration needs to be much greater than that of the target.

Fig.28 Trajectories with parameters shown in Table 5 except

Fig.29 Time-to-go with parameters shown in Table 5 except

Example 4The initial conditions are given in Table 6.We test the attacker’s optimal one-to-one pursuit guidance law and the guidance law identified in(46)by using nonlinear simulation.

Table 6 Initial parameters for Example 4

Fig.30 and Fig.31 show the trajectories for the two guidance laws,respectively.It can be observed that no matter which guidance law is used,the attacker can intercept the target.As shown in Fig.31,using the guidance law corresponding to(46)damages the collision triangle between the at tacker and the target,and the evasive distance is much smaller than that when using the optimal one-to-one pursuit guidance law as shown in Fig.30.Under these parameters,using the optimal one-to-one guidance law damages the collision triangle slightly and the attacking miss distance is smaller.

Fig.30 Trajectories by using the optimal pursuit guidance law

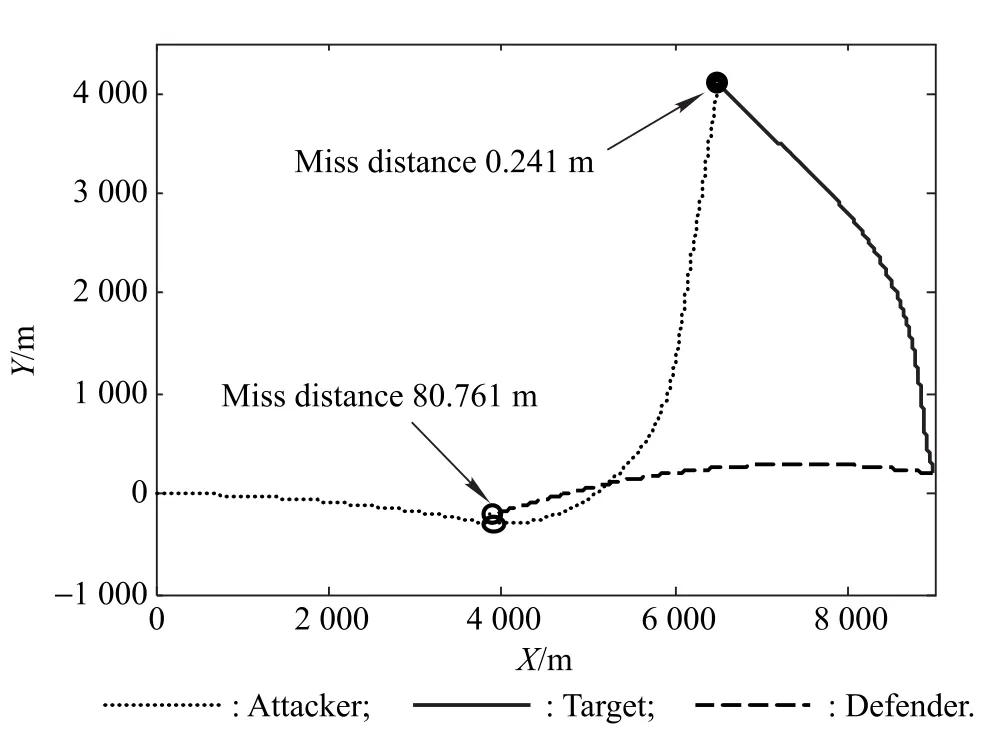
Fig.31 Trajectories by using(46)

Fig.32 and Fig.33 show the trajectories for the two guidance laws,respectively,for the case when the maximal acceleration of the attacker is 80 m/s2.It can be observed that by decreasing the maximal acceleration of the attacker,the optimal pursuit guidance law still can accomplish the task as shown in Fig.32.However,the guidance law corresponding to(46)fails;this is because the guidance law corresponding to(46)requires that the attacker’s maximal acceleration should be much greater than that of the target.Thus,we can choose a reasonable pursuit acceleration within the maximal acceleration for the attacker to win the game,such as the circumstances shown in Fig.32.If the maximal acceleration of the attacker is 180 m/s2,we choose 80 m/s2as the pursuit acceleration.Hence,we can conclude that if the signs ofZAT(t=0)andZAD(t=0)are the same,for some instances,the attacker,it is not necessary for the attacker to evade the defender first.

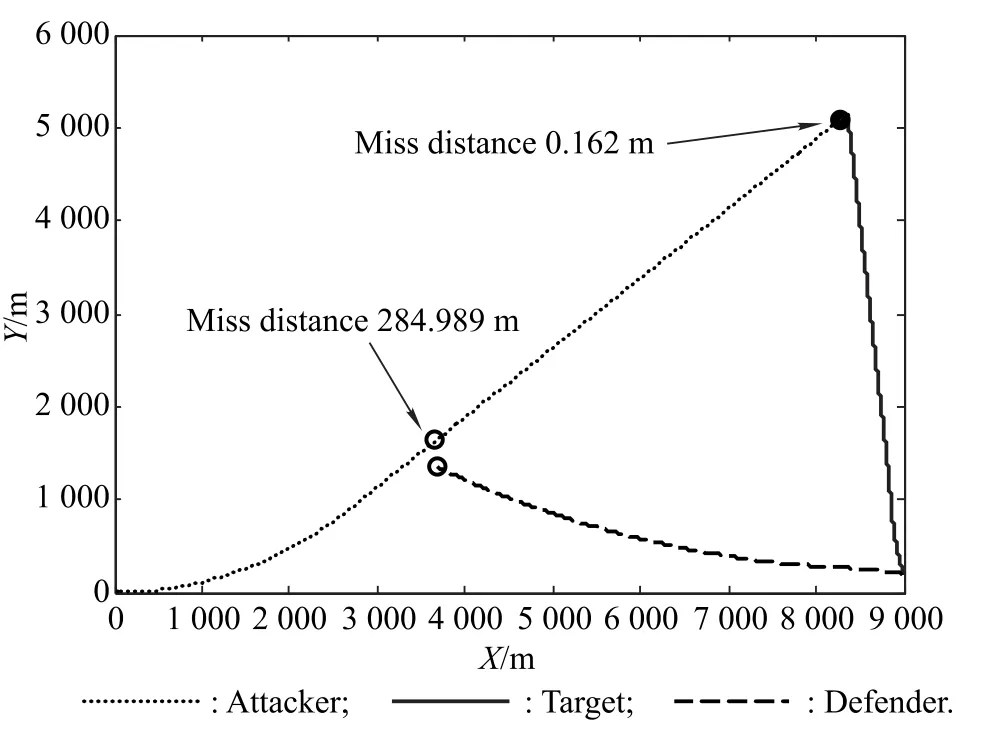
Fig.32 Trajectories by using the optimal pursuit guidance law with parameters given in Table 6 except

Fig.33 Trajectories by using(46)with parameters given in Table 6 except

Although under these parameters, using the optimal pursuit guidance law is better than using the guidance law corresponding to(46),and in some cases using the guidance law from(46)cannot intercept the target,this guidance law can win the optimal pursuit guidance law in some cases such as the one given in Example 3.Fig.34 and Fig.35 show the trajectories of the three players by using the optimal guidance law with the pursuit acceleration being 150 m/s2and 180 m/s2,respectively.It can be observed that the attacker cannot accomplish the attacking task.Meanwhile,even if the attacker’s maximal acceleration becomes greater,the miss distance between the attacker and the defender cannot increase to a safe range.This is because when the attacker uses the optimal one-to-one guidance law to pursue the target,the acceleration is restricted byZAT.However,under the parameters given in Example3,the derived guidance of(46)can accomplish the task.

Fig.34 Trajectories by using the optimal pursuit guidance law with parameters given in Table 5

Fig.35 Trajectories by using the optimal pursuit guidance law with parameters given in Table 5 except

6.Conclusions

Guidance laws are investigated for the attacker to win a game involving an attacker,a defender and a target.The game occurs in the endgame;thus,we derive the guidance laws by using linear dynamics and investigate them by using nonlinear simulation.When the signs ofZAT(t=0)andZAD(t=0)are opposite,the attacker uses the optimal one-to-one guidance law to pursue the target and simultaneously evades the defender.When the signs ofZAT(t=0)andZAD(t=0)are the same,the attacker uses the optimal one-to-one guidance law to pursue the target but simultaneously performs the worst with respect to the defender.However,the at tacker can still accomplish the task under some conditions,specifically when the initialZAD(t=0)is a relatively large value or when a relatively small value underZAT(t=0)is reasonable.For this case,the collision triangle is slightly damaged and the acceleration of the attacker does not have to be much greater than that of the target.In this scenario,we only need to choose a reasonable pursuit acceleration within the maximal acceleration for the attacker.Thus,it is not necessary for the attacker to evade the defender first because the guidance law defined in(46)damages the collision triangle heavily,and the acceleration needed by the attacker is much greater than that of the target,as indicated in Example4.However,for some situations,such as in Example 3,it is difficult to accomplish the task if the attacker is only assigned to a pursuit acceleration within the maximal acceleration.For this case,we need to use the guidance law defined in(46)to accomplish the task,as shown in Fig.25.

Thus,in reality,we need to choose reasonable guidance laws for the attacker to win a game under different conditions.The investigation and the derived guidance laws have potential for use in pursuit-evasion problems.

[1]PENG S,PANL,HU T,et al.New three-dimensional guidance law for BTT missiles based on differential geometry and Lie group.Journal of Systems Engineering and Electronics,2011,22(4):684–690.

[2]SONG J,SONG S.Three-dimensional guidance law based on adaptive integral sliding mode control.Chinese Journal of Aeronautics,2016,29(1):2–14.

[3]LI R,XIA Q,WEN Q.Extended optimal guidance law with impact angle and acceleration constriants.Journal of Systems Engineering and Electronics,2014,25(5):868–876.

[4]LIU Y,QI N,TANG Z.Linear quadratic differential game strategies with two-pursuit versus single-evader.Chinese Journal of Aeronautics,2012,25(6):896–905.

[5]KUMKOV S S,MENEC S L,PATSKO V S.Solvability sets in pursuit problem with two pursuers and one evader.IFAC Proceedings Volumes,2014,47(3):1543–1549.

[6]KUMKOV S S,MENEC S L,PATSKO V S.Level sets of the value function in differential games with two pursuers and one evader,interval analysis interpretation.Mathematics in Computer Science,2014,8(8):443–454.

[7]XIAO B S,FANG Y W,HU S G,et al.Decision methods for cooperative guidance in multi-aircraft air warfare.Systems Engineering and Electronics,2009,31(3):610–612.(in Chinese)

[8]FUCHS Z E,KHARGONEKAR P P,EVERS J.Cooperative defense within a single-pursuer,two-evader pursuit evasion differential game.Proc.of the 49th IEEE Conference on Decision and Control,2011:3091–3097.

[9]SCOTT W,LEONARD N E.Pursuit,herding and evasion:a three-agent model of caribou predation.Proc.of the American Control Conference,2013:2978–2983.

[10]BOYELL R L.Defending a moving target against missile or torpedo attack.IEEE Trans.on Aerospace and Electronic Systems,1976,12(4):522–526.

[11]BOYELL R L.Counter weapon aiming for defense of a moving target.IEEE Trans.on Aerospace and Electronic Systems,1980,16(3):402–408.

[12]SHINAR J,SILBERMAN G.Discrete dynamic game modelling anti-missile defense scenarios.Dynamics and Control,1995,5(1):55–67.

[13]RUSNAK I.The lady,the bandits and the body-guard game.Proc.of the 44th Israel Annual Conference on Aerospace Science,2004:25–26.

[14]RUSNAK I.The lady,the bandits and the body guards-a two team dynamic game.IFAC Proceedings Volumes,2005,38(1):441–446.

[15]RUSNAK I.Games based guidance in anti-missile defence for high order participants.Proc.of the 15th IEEE Mediterranean Electrotechnical Conference,2010:812–817.

[16]RATNOO A,SHIMA T.Line-of-sight interceptor guidance for defending an aircraft.Journal of Guidance,Control,and Dynamics,2011,34(2):522–532.

[17]FISAC J F,SASTRY S S.The pursuit-evasion-defense differential game in dynamic constrained environments.Proc.of the 54th IEEE Conference on Decision and Control,2015:4549–4556.

[18]PROKOPOV O,SHIMA T.Linear quadratic optimal cooperative strategies for active aircraft protection.Journal of Guidance,Control,and Dynamics,2013,36(3):753–764.

[19]RATNOO A,SHIMA T.Guidance strategies against defended aerial targets.Journal of Guidance,Control,and Dynamics,2012,35(4):1059–1068.

[20]RUBINSKY S,GUTMAN S.Three body guaranteed pursuit and evasion.Proc.of the AIAA Guidance,Navigation,and Control Conference,2012:1–24.

[21]RUBINSKY S,GUTMAN S.Three player pursuit and evasion conflict.Journal of Guidance,Control,and Dynamics.2014,37(1):98–110.

[22]GARCIA E,CASBEER DW,PHAM K,et al.Cooperative aircraft defense from an attacking missile.Proc.of the 53th IEEE Conference Decision and Control,2014:2926–2931.

[23]GARCIA E,CASBEER D W,PACHTER M.Active target defense differential game with a fast defender.Proc.of the American Control Conference,2015:3752–3757.

[24]GARCIA E,CASBEER D W,PACHTER M.Cooperative strategies for optimal aircraft defense from an attacking missile.Journal of Guidance,Control,and Dynamics,2015,38(8):1510–1520.

[25]KUMAR S R,SHIMA T.Cooperative nonlinear guidance strategies for aircraft defense.Journal of Guidance,Control,and Dynamics,2017,40(1):124–138.