Discrete decision model and multi-agent simulation of the Liang Zong two-chain hierarchical organization in a complex project

MAI Qiang,ZHAO Yueqiang,and AN Shi

1.School of Management,Harbin Institute of Technology,Harbin 150001,China;2.Defense Technology Academy,China Aerospace Science&Industry Corporation,Beijing 100854,China

1.Introduction

Complex projects,also called mega-projects,include bridges,super hydropower stations,and space station projects and the like;they involve complex processes and are major undertakings[1].One reason for the complexity of such projects is that they are divided into many interrelated sub-jobs[2].Faced with such a problem,organizations engage in a search process to find the right decisions[3].Normally,a hierarchical organization is constructed to speed the search process[4].In a normal hierarchical organization,there is only one decision maker on each node[5].This kind of topology structure assumes there is just one project manager on each level of the hierarchical structure and that the manager should make all the decisions.

Almost all studies on hierarchical organizations assume that these decisions are homogeneous[6–8].Therefore,there is just one chain in an hierarchical organization,and every manager in the chain makes just one kind of decision.In fact,there are many heterogeneous decisions in the search process of a complex project,such as technique selection,budget allocation,schedule plan,and so forth[9,10].These decisions can be classified into two kinds[11]:technical decisions,such as the span of a bridge,the altitude of a dam,or the weight of a load,and administrative decisions,such as the budget allocation and the schedule plan.These two kinds of decisions are also interrelated.

In order to consider the difference and the interdependency between technical and management decisions,a two-chain hierarchical organization structure known as Liang Zong is used in complex projects in China[12–14].In contrast to the single-chain hierarchical organization,this kind of organization has two cooperative hierarchical chains:the chief-engineer chain,which consists of chief engineers who are responsible for dealing with technical problems in each institution of the hierarchical organization and who are always famous experts in one technical field,and the general-director chain, which consists of general directors who are normally the administrative authorities in each institution.In this way,the two chains have decision makers in every institution.Thus,everyone in the organization has two cooperative obligations: first,they should cooperate in their chains vertically;second,they should cooperate in their institutions horizontally.

However,there is still the question of whether the Liang Zong two-chain hierarchical organization is an efficient organization in the search process.In order to prove the efficiency of the two-chain hierarchical organization,we model the search process of this kind of organization using a discrete dynamic model to show how it reduces the complexity of the process.We also prove the efficiency of the two-chain hierarchical organization through a simulation.

In the following,we first survey the related works.Section 3 describes the two-chain hierarchical organization by examining the case of the Chang’e-1 Satellite Project,the first project of China’s Lunar Exploration Program,and showing the practical search process and the communication mechanism in this organization.Then,we propose the search process model in two different hierarchical organizations.In Section 4,the model is simulated to show the different results in different kinds of organization.Finally,we conclude the research and provide directions for future work in Section 5.

2.Related works

The organization search process is a dynamic procedure to find a set of satisfactory solutions used by a group of bounded rational decision makers who are responsible for one subsystem of a system[4,15].The process is needed because no one person can finish a whole project on their own[4].During the process,the decision of one decision maker is dependent on the decisions of other ones because of the interdependency of the subsystems.

Thus,how to organize decision makers to make the search process efficient is an important question.Many researchers have found or compared ways to improve the search process.Siggelkow and Rivkin studied how the turbulence and the complexity of the environment affect the search performance[7].Baumann and Siggelkow studied whether a problem solver should expand the search domain in the search process[16].Chandrasekaran et al.studied the dynamics of the search processes of R&D projects when the level of complexity shifts[17].Some studies discussed the trade-off between the delegation and the control of authority and indicated a hierarchical organization for search.Simon thought that the hierarchical structure is the inevitable selection when facing complex problems for mankind[15].Corominas-Murtra et al.proved that the hierarchical structure is the result of organizational revolution under a number of deep constraints[18].The hierarchical organization has also been proved to be an efficient way to speed up research while sacrificing the quality of decisions[5,19].However,these studies only considered the interdependence of decision makers,neglecting the interdependence of different kinds of decisions.That is to say,in the traditional research about the search process in a hierarchical organization,decisions were assumed to be homogeneous.

In a complex project,not only the decision makers in the organization but also the heterogeneous decisions of each decision maker are interrelated[20,21].Dillon et al.divided those decisions into technical and management decisions and proposed an advanced programmatic risk analysis and management(APRAM)model which considers the trade-off between them in a failure risk framework[11].In this way,some optimization models were proposed by considering the interdependence of different elements in a project[4,22–25].These studies sought to find the optimal decisions through optimization but ignored the dynamic characteristics of the search process in a complex project.

Considering the interdependence between technical and management decisions,a two-chain hierarchical organization has been proposed in China;this type of organization is used for complex projects,especially in the space industry.To the best of our knowledge, the efficiency of this kind of organization has not been studied.Therefore,this paper will show the complexity reduction effect caused by the two-chain hierarchical organization and highlight the efficiency of this Chinese organization innovation in complex projects.

3.Two-chain organization structure in complex projects

The two-chain organization structure,also called the Liang Zong system,has been used in Chinese space engineering since the1960s[26].Because of the success of the Chinese space industry and its great influence in China,many urban infrastructure projects also adopted this kind of organization structure.

The two-chain organization structure has two features.First,the organization is still a hierarchical structure,which is the same as the organization of Western projects.From top to bottom,every node of the tree-like structure has a project manager who makes the decisions about the module he/she controls. Second, the basic feature of the or-ganization structure is that there are two managers on every node of the hierarchical structure:the chief engineer,who is responsible for the technical decisions about the module under his/her control,and the general director,who is responsible for the management decisions.Therefore,there are two chains along the hierarchical structure:the chief engineer chain and the general-director chain[27].

China’s Chang’e-1 satellite,the first stage of the country’s Lunar Exploration Program,is a complex project whose purpose is to launch the first Chinese lunar probe into the lunar orbit[28].As shown in Fig.1,the project has five systems:a satellite system,a rocket system,a launch system,a telemetry-track-command(TT&C)system,and an application system.Each system also has many subsystems under the control of the higher-level system:for example,the satellite system has structure,attitude and orbit control,and power subsystems[29].

Fig.1 Module of the Chang’e-1 satellite

During the whole search period of the project,every research institute or factory that is responsible for the R&D or manufacture of a system or subsystem would assign a chief engineer and a general director for the project.The supreme administrative authority of the Chang’e 1 satellite project is the Center for the Lunar Exploration Program.The center has two famous experts in the Chinese space industry who are responsible for the whole project:Luan Enjie,who is the general director of the project,and Sun Jiadong,who is the chief engineer of the project[27].At the system level,there is a same organization setup as that at the center:for example,the China Academy of Space Technology,which is responsible for the R&D of the satellite system,also establishes a management team consisting of a general director and a chief engineer.In this way,a two-chain organization structure is formed along with the hierarchical structure of the whole project,as shown in Fig.2.Each decision maker in the organization is influenced not only by the decision maker on the same level but also by the decision makers in the same chain.First,the search process is a top-down sequence process,which means the upper level project team should consider optimizing the whole performance of the module they control.In practice,the general director and the chief engineer in the same system should make an agreement about decisions in their system.Second,the information report is down-top,which means the lower level decision maker should report their performance to the next level up in their decision maker chain.In practice,there is a scheduled meeting mechanism in each chain and an ad hoc meeting mechanism for emergency situations.This can be seen as the communication mode in this kind of organization.

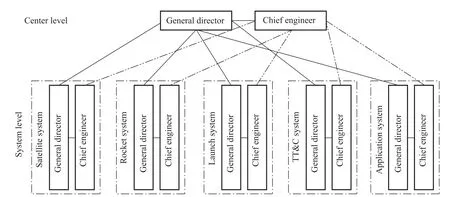
Fig.2 Two-chain organization structure of the Chang’e-1 Satellite Project

Under this kind of two-chain hierarchical organization structure that considers the interdependence between technical decisions and management decisions,the search process and its results are definitely different from those in a one-chain hierarchical structure.

4.Discrete decision model

Under a two-chain hierarchical organization structure,the search process is a complex process because of the interdependence of technical and management decisions.A mathematical model,a discrete decision model to be precise,will be proposed to illustrate the search process under such a complex system.

4.1 Complex system

We assume that a design search process is taking place in a hierarchical organization in which each subsystem is facing two interrelated jobs:one is a technical decision,the other is a management decision.Thus,a two-chain hierarchical organization is coming into being.From the horizontal view,there are two kinds of decision makers in each subsystem:(i)the chief-engineer decision makers,consisting of one chief engineer and some vice-chief engineers who are responsible for the technical problems of the subsystem,such as technique proposals and decisions;(ii)the general-director decision makers,consisting of one general director and some deputies who are responsible for the schedule,budget,and so forth for their own subsystem.From the vertical view,there is a superposed two-chain hierarchicalorganization. The first chain is the chief engineer hierarchical chain, which consists of the chief engineer decision makers of every subsystem.The other is the general director hierarchical chain,which has the same structure as the chief engineer hierarchical chain.

A feature of this two-chain hierarchical organization structure is complex interdependency.Every decision maker,no matter whether the chief engineer or the general director,is influenced by three other decision makers:the other kind of decision maker in the same subsystem;a counterpart in the upper level of the same hierarchical chain;and a counterpart in the upper level of the other hierarchical chain.

The search process in this complex relational network is complex because of the above interrelationships.The interdependency in the two-chain hierarchical structure determines the scale of the search space,which is huge in this situation.During the search process,every decision maker can be assigned a random performance contribution according to the interdependency of decisions.In this way,the performance dimension of a decision maker is determined by the dimension of the search space.Once the interrelated decision maker changes his/her decision,the performance of the decision maker should also be changed to a new one.However,the search would not be guaranteed to reach the most optimal performance contribution for every decision maker.The search in a predetermined random space for every decision maker is like walking on a multidimensional fitness landscape which consists of many valleys and peaks[30].The peak which a decision maker climbs up may be not the highest peak of the landscape.Thus,the search process may fall into a local optimal result because of the non-linear search process.

4.2 Search process

We assume that the hierarchical structure of a complex project has M levels and that each higher-level decision maker controls N decision makers on the lower level.Therefore,there aredecision makers in the whole project.

In this hierarchical structure, decision maker aij(the jth decision maker located on the ith level)has one higher level“interrelated decision maker”,N-1 interrelated decision makers in the same level,and N lower-level interrelated decision makers.In total,there are 2N interrelated decision makers for decision maker aij,except for decision maker a11(the top decision maker)and am-1,j(the bottom decision makers),who just have N interrelated decision makers.

During the search process,every decision maker searches for a higher performance in a predefined search space which reflects the interdependency among the decisions of interrelated decision makers.The process has five steps.

Step 1Ascertain the interrelated decision makers according to hierarchical interdependency.Assume decision maker aijis the jth decision maker in on the ith level.Then,the interrelated decision maker on the higher-level isi,j,the interrelated decision makers on the lower-level arei,j,and the interrelated decision makers on the same level arei,j.The whole interrelated decision maker set for decision maker aijis Aij={ij,ij,aij},which has 2N elements.For example,a decision maker a21located in the 2nd level has three interrelated decision makers on the same level and controls four sub-decision makers on the lower level.The interrelated decision maker set is A21={a11,a22,a23,a24,a31,a32,a33,a34}.

Step 2Define the search space.For simplicity,we can assign a binary variable to the state of each decision maker randomly at the start of the search.This means that the state of each decision maker sijin interrelated decision maker set Aijis also a binary variable sij∈{0,1}.Because there are 2N elements in the decision maker set,the state space Sijfor Aij,or the named search space,has 22Ndifferent kinds of combination of binary variables.For example,the interrelated decision makers set S21has 28kinds of set,one of which may be S21={0,1,0,0,0,0,0,0}when each element of A21is assigned a different binary variable.

Step 3Define the performance contribution set.The performance contribution set Pijalso has 22Ndifferent elements which are assigned randomly as a random variable pij∈[0,1].For the performance of each decision maker aij,pijis determined by the state set of Sij.In this way,one combination set of Sijcorresponds to one performance contribution of Pij.For example,S21={0,1,0,0,0,0,0,0}corresponds to a performance contribution p21=0.665 7,which is determined randomly.

Step 4Calculate the average performance of the whole system.The average performance of the whole system is the arithmetic mean of all decision makers on the hierarchical structure

Step 5Start the search in the state space.Because of the interdependence, once we change the state of a decision maker (choose the other number of the binary variable),the state sets of some interrelated decision maker sets,including the decision maker,should change to another state set.Thus,the performance contribution of the decision makers determined by those interrelated decision maker sets would change as well.For example,once we change the state of the second interrelated decision maker in S21,the state of S21will change to S21={0,0,0,0,0,0,0,0}.Then,the performance contribution p21of a21would change to p21=0.854 2,which is a predefined random number.The performance contributions of some other decision makers interrelated with a21should also be changed.

Step 6Search in the state space.Calculate the new average performance of the whole systemWhen≥accept the last changed state of the decision maker.When＜do not accept the last changed state of the decision maker and go back to the previous state.For example,whenS21={0,0,0,0,0,0,0,0}will be accepted for decision maker a21.However,once＜the state set will be changed back to S21={0,1,0,0,0,0,0,0}and the performance contribution will still be p21=0.665 7.

Fig.3 Search process in a hierarchical structure

Step 7Go back to Step 4 to start a new change until the performance contributions of all decision makers do not change,which means the average performance of the whole systemwould not change anymore.

The above process is shown in Fig.3.

4.3 Search patterns

When considering the interdependence between the technical decision tijand the management plan mij,there are two kinds of hierarchical organization structure,and this means that there are different search patterns.

4.3.1 Single-chain search pattern

In this search pattern,the decision maker makes the tijand mijdecisions at the same time.According to the above search pattern and the search process,the interrelated decision setchanges to Aij=The objective for aijis to find a decision set to optimize the average performance of the whole system:

Because we divide every decision in Aijinto two parts,the interdependence will be increased to 4N+1 elements.There will be 24N+1different kinds of combination of binary variables and 24N+1different performance contributions for

4.3.2 Two-chain search pattern

In this search pattern,the chief engineer or general director in a unit respectively make the technical decision tijand the management plan mij.In this search pattern,the interrelated decision set is also Aij=However,the two-chain pattern divides the whole set into two different subsets Aij=The objective for the two decision makers is to find a decision set to optimize the average performance of the whole system:

We can see from the above equations that the interdependence is just 2N+1 under the two-chain hierarchical structure.That is to say,there are just 22N+1different kinds of combination of binary variables and 22N+1different performance contributions forCompared with element number 24N+1under the single-chain search pattern,the search space is reduced substantially.

5.Simulation

When considering the search strategy in the two-chain organization structure,the process is more complex.It cannot be directly modelled as a mathematical model.Thus,we conduct the study through a simulation method using Netlogo 5.3.1.It costs almost 100 hours to run all of the simulation on a contemporary computer with an Intel i5-5200UCPU and a 4GB memory.Below,we also verify the result through a sensitivity analysis,which costs another 50 h.The program and all the data are available from the authors.

5.1 Search strategy

Under the two-chain hierarchical organization structure,there are two kinds of optimization search strategies.

The first strategy is the horizontal optimization search.On each node of the hierarchical organization structure, the general director and the chief engineer should get the trade off between management and technical decisions to optimize the whole performance contribution of their subsystem,which is calculated as the average value of the performance contributions of the two decision makers.This kind of system performance is also adopted by Chandrasekaran et al.[17].When the optimum is found,the state of the“horizontal decision maker”should be fixed.

Then,the second optimization search strategy,the vertical optimization search,should be started.The fixed state of the lower-level decision maker will be reported to the higher-level counterpart along the hierarchical chain.That is to say,the higher-level decision maker would receive decision information from the lower level decision makers he/she controls.Then,the higher level decision maker would search to optimize the performance contribution of the chain from the perspective of his/her chain.When the optimum is found,the state of the higher-level decision maker should be fixed.

After that,the horizontal optimization search of the upper level of the hierarchical structure should be started.In this way,the horizontal and vertical optimization searches would take place in turn from the lowest subsystem of the hierarchical organization structure until the process reaches the top or the central control node of the system.

Fig.4 shows the complicated optimization search strategy in the two-chain structure.During the simulation,we propose two kinds of evaluation indexes for comparing the two kinds of hierarchical structure.The first index is the number of iterations required to reach a stable position.This index represents the complexity of the search process.The second index is the result of the performance contribution of the whole system.Like the number of iterations,the performance contribution is also a random variable whose probability distribution function(PDF)features are used to reflect the efficiency of the two-chain hierarchical structure.

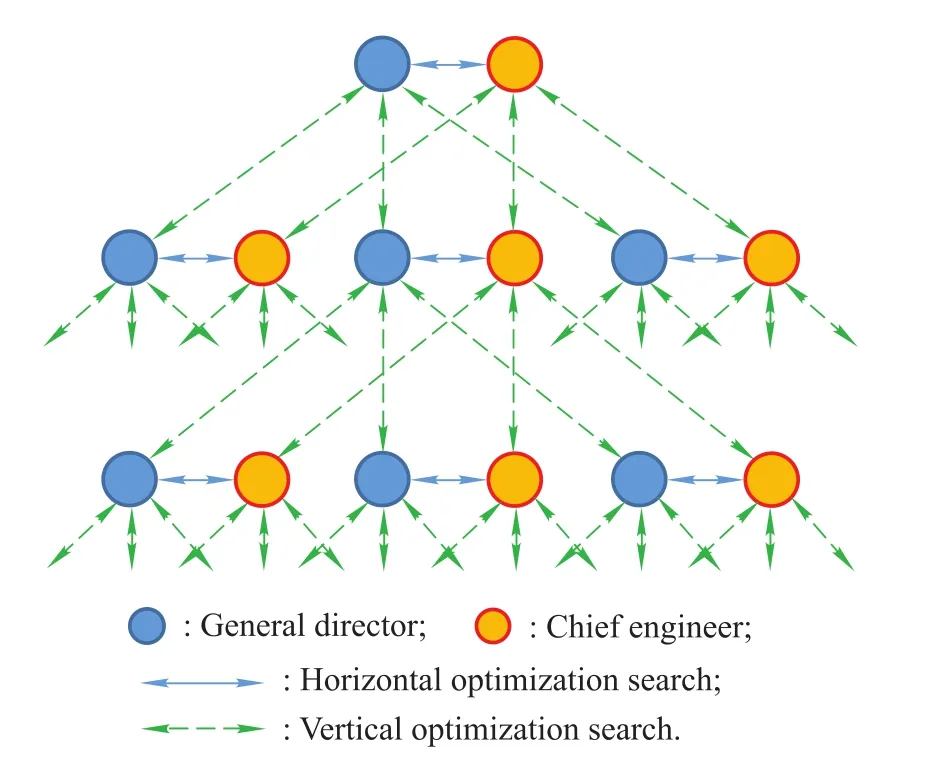
Fig.4 Search strategy in the two-chain hierarchical structure

5.2 Simulation result

In order to show the efficiency of the two-chain organization,we compare the two kinds of organization structure in different hierarchical structures,as shown in Fig.5.

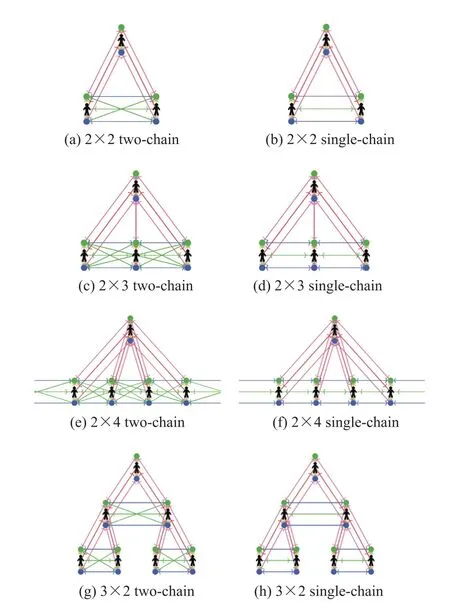
Fig.5 Different hierarchical organizations

5.2.1 Number of iterations

For each kind of hierarchical organization,we simulate 100 times until the whole system reaches an optimal performance,which means the search process oriteration process should stop.Table 1 shows the distribution type,the mean,and the standard deviation of the number of iterations for each hierarchical structure.

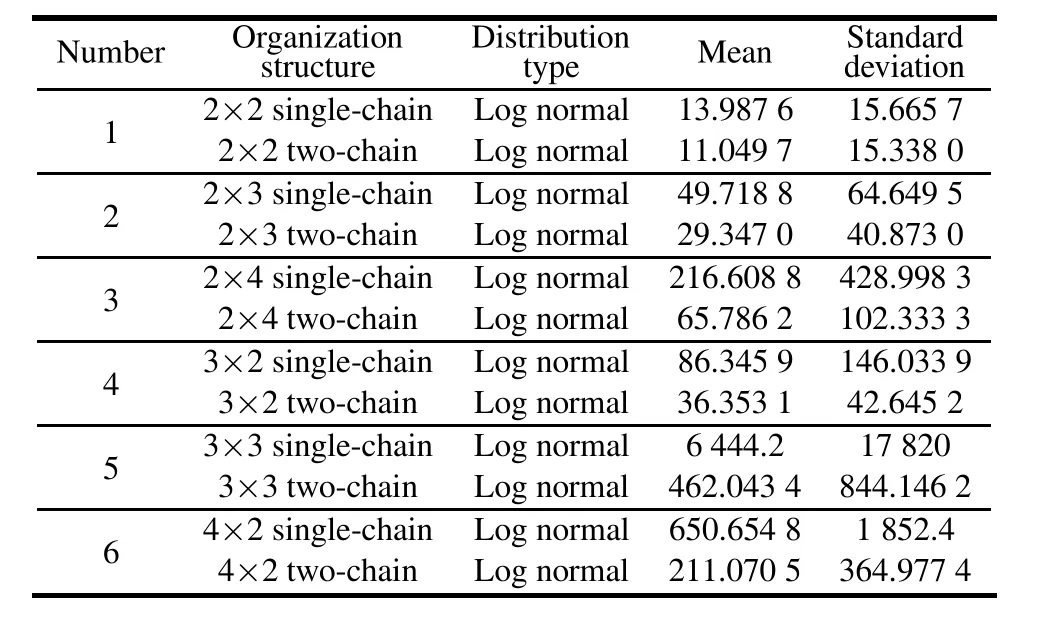
Table 1 Distribution of the number of iterations of different hierarchical organization structures(at 95%confidence level)

Fig 6.shows the mean and the standard deviation of two kinds of hierarchical organization structures.

Fig.6 Iteration mean and standard deviation of two kinds of hierarchical organization structures

Because the number of iterations has a log-normal distribution,we can obtain the PDF for every kind of hierarchical organization in each structure,as shown in Fig.7.

Fig.7 PDF of the number of iterations for two kinds of hierarchical organization structures

We also conduct an experiment in which we just focus on the stable point or a local optimal point given a fixed search space.Fig.8 shows the stable points of two kinds of hierarchical organizations in four structures.It also reflects the shape of the fitness landscape in each search.

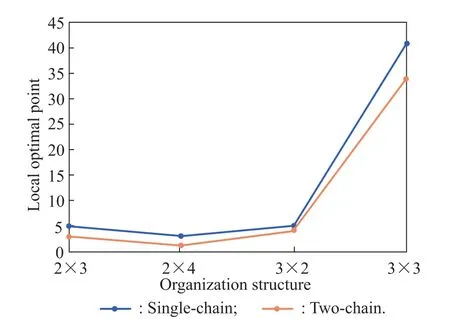
Fig.8 Local optimal points of two kinds of hierarchical organization structures

5.2.2 System performance

Finally,we check the impact of the two kinds of hierarchical organizations on performance.We use the same simulated data as in the first simulation experiment.Table 2 shows the distribution feature of the performance of different hierarchical organization structures.

Table 2 Distribution of performance of different hierarchical organization structures(at 95%confidence level)

Fig 9.shows the mean and the standard deviation of two kinds of hierarchical organization structures.

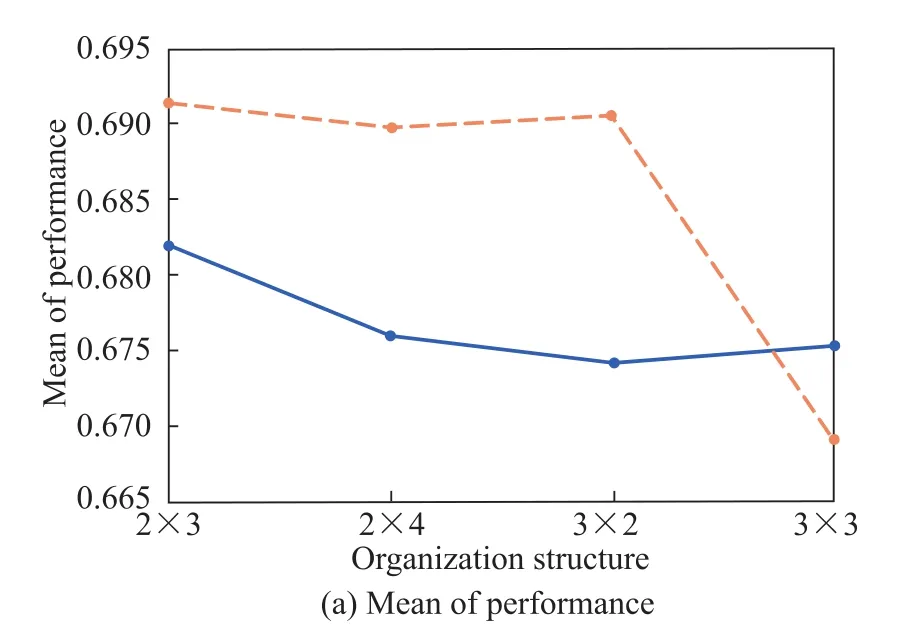
Fig.9 Mean and standard deviation of the performance of two kinds of hierarchical organization structures

5.3 Analysis of results

According to the above simulations,there are three findings we can obtain by comparing the number of iterations and the performance of different hierarchical organizations in different structures.

The first finding is that the more complex the organization is,the greater the number of iterations a search has,no matter what the type of hierarchical organization is.This finding has been reported in other studies about search in complex projects[5].Also,we can see that when the hierarchy increases to 3,the number of iterations will increase quickly to a very huge number.The phenomenon is similar to the exponential function of the search space in the NK model.

The second finding is that a two-chain hierarchical organization can reduce the number of iterations efficiently,and the more complex an organization is,the more obvious the effect is.This phenomenon means that the search process would converge to a stable point more quickly in a two-chain hierarchical organization than in a single-chain hierarchical organization.At the same time,the fluctuation is also decreased in a two-chain hierarchical organization,which means that the search process should be more stable.

We also check the reasons for this phenomenon.Fig.7 shows that in the same organizational structure,the PDF of the number of iterations of a two-chain hierarchical organization is sharper than that of a single-chain hierarchical organization.The difference means that the fitness landscape of the search in a two-chain hierarchical organization has few peaks or valleys.It is quicker to converge to a local optimal point or a local peak in a “hill-like”landscape.The simulation in a given search space also proves the phenomenon.We find that although the local optimal point increases with the increasing of the complexity of the structure,the local optimal point in a two-chain hierarchi-cal organization is always lower than that in a single-chain hierarchical organization.

The third finding is that the performance of a hierarchical organization can be improved.However,when the two chain organization is very complicated,the performance of the system may be worse than that of a single-chain hierarchical organization.In Fig.9,the mean of the performance of a two-chain hierarchical organization in a 3×3 structure is 0.668 9 while that of a single-chain hierarchical organization is 0.675 3.This phenomenon shows us that although the two-chain hierarchical organization can reduce the number of iterations and accelerate the search speed,the performance of the search may not be improved.

Our research proves the efficiency of the two-chain hierarchical organization for complex projects which should consider the trade-off between technical and management decisions for each decision maker.These findings can help organization designers of complex projects,such as space engineering and cross-sea bridges,to organize their control and command chain to accelerate the search process or trade-off the speed and performance of the project.The most concise way is to allocate a chief engineer,who is responsible for technical problems,and a general director,who is responsible for management matters,in every institution along the hierarchical organizational structure.

6.Conclusions

This study examines the search dynamics of a two-chain hierarchical organization,which is always adopted in complex projects in China.First,we prove that the two-chain hierarchical organization can reduce the complexity of the search in an NK framework model,the reason is that the search space is reduced by a large amount when the technical and management decisions are separated into different chains which are interdependent within the institution.Second,we examine the efficiency of the two-chain hierarchical organization by simulation.The results of the simulation prove the iteration reduction effect(accelerating the speed of search)caused by the two-chain hierarchical organization.The dynamic mechanism is also revealed by the simulation.We find that the fitness landscape is a smoother hill-like landscape in a two-chain hierarchical organization,while in a single-chain hierarchical organization,the fitness landscape is a cliffy and mountain-like with more peaks and valleys.However,as a cost,the performance of a search process is not guaranteed to improve when the search speed is accelerated.The study proves the rationality of the two-chain hierarchical organization normally used in complex projects in China,which has been neglected by the global academic field for a long time.The simulation model used here does not consider the information asymmetry problem in an organization and only uses one kind of search strategy.The information asymmetry problem and a more complicated search strategy should be considered in future research.

[1]FLYVBJERG B,GARBUIO M,LOVALLO D.Delusion and deception in large infrastructure projects:two models for explaining and preventing executive disaster.California Management Review,2009,51(2):170–193.

[2]NADLER D,TUSHMAN M,NADLER M B.Competing by design:the power of organizational architecture.New York:Oxford University Press,1997.

[3]FLEMING L,SORENSON O.Technology as a complex adaptive system:evidence from patent data.Research Policy,2001,30(7):1019–1039.

[4]RIVKIN J W,SIGGELKOW N.Balancing search and stability:interdependencies among elements of organizational design.Management Science,2003,49(3):290–311.

[5]MIHM J,LOCH C H,WILKINSON D,et al.Hierarchical structure and search in complex organizations.Management Science,2010,56(5):831–848.

[6]LEVINTHAL D A.Adaptation on rugged landscapes.Management Science,1997,43(7):934–950.

[7]SIGGELKOW N,RIVKIN J W.Speed and search:designing organizations for turbulence and complexity.Organization Science,2005,16(2):101–122.

[8]KNUDSEN T,LEVINTHAL D A.Two faces of search:alternative generation and alternative evaluation.Organization Science,2007,18(1):39–54.

[9]BACCARINI D.The concept of project complexity—a review.International Journal of Project Management,1996,14(4):201–204.

[10]PICH M T,LOCH C H,MEYER A D.On uncertainty,ambiguity,and complexity in project management.Management Science,2002,48(8):1008–1023.

[11]DILLON R L,PAT-CORNELL M E,GUIKEMA S D.Programmatic risk analysis for critical engineering systems under tight resource constraints.Operations Research,2003,51(3):354–370.

[12]WANG J.The adoption of the ‘Liang Zong’management framework in smart city engineering.http://www.chyxx.com/news/2012/0112/142287.html.(in Chinese)

[13]XU Q,WANG W,WANG X B.The communication mechanism between technical and management high level talents through the train of‘Liang Zong’.Aerospace Industry Management,2010,18(7):17–19.(in Chinese)

[14]ZENG Z H,TANG W,YIN J.Analysis of promotion path and period of‘Liang Zong’inspace engineering.Aerospace Industry Management,2014,2:12–15.(in Chinese)

[15]SIMON H A.The architecture of complexity.Proceedings of the American Philosophical Society,1962,106(6):467–482.

[16]BAUMANN O,SIGGELKOW N.Dealing with complexity:integrated vs.chunky search processes.Organization Science,2013,24(1):116–132.

[17]CHANDRASEKARAN A,LINDERMAN K,STING F J,et al.Managing R&D project shifts in high-tech organizations:a multi-method study.Production and Operations Management,2016,25(3):390–416.

[18]COROMINAS-MURTRA B,GOI J,SOLR V,et al.On the origins of hierarchy in complex networks.Proceedings of the National Academy of Sciences,2013,110(33):13316–13321.

[19]DOBRAJSKA M,BILLINGER S,KARIM S.Delegation within hierarchies:how information processing and knowledge characteristics influence the allocation of formal and real decision authority.Organization Science,2015,26(3):687–704.

[20]BABU A,SURESH N.Project management with time,cost,and quality considerations.European Journal of Operational Research,1996,88(2):320–327.

[21]KHANG D B,MYINT Y M.Time,cost and quality trade-off in project management:a case study.International Journal of Project Management,1999,17(4):249–256.

[22]DILLON R L,PAT-CORNELL M E,GUIKEMA S D.Optimal use of budget reserves to minimize technical and management failure risks during complex project development.IEEE Trans.on Engineering Management,2005,52(3):382–395.

[23]RAMIREZ-MARQUEZ J E,SAUSER B J.System development planning via system maturity optimization.IEEE Trans.on Engineering Management,2009:56(3),533–548.

[24]GARBER R,PAT-CORNELL E.Shortcuts in complex engineering systems:a principal-agent approach to risk management.Risk Analysis,2012,32(5):836–854.

[25]ZEYNALIAN M,TRIGUNARSYAH B,RONAGH H R.Modification of advanced programmatic risk analysis and management model for the whole project life cycle’s risks.Journal of Construction Engineering and Management,2012,139(1):51–59.

[26]HUANG X.Career development puzzle and solution of Aerospace’s ‘Liang Zong’system.http://www.spacechina.com/n25/n144/n206/n214/c66424/content.html.(in Chinese)

[27]BESHA P.Policy making in China’s space program:a history and analysis of the Chang’e lunar orbiter project.Space Policy,2010,26(4):214–221.

[28]ZHENG Y,OUYANG Z,LI C,et al.China’s Lunar Exploration Program:present and future.Planetary and Space Science,2008,56(7):881–886.

[29]LUAN E J.Aerospace systems engineering.Beijing:China Astronautic Publishing House,2010.(in Chinese)

[30]KAUFFMAN S A,WEINBERGER E D.The NK model of rugged fitness landscapes and its application to maturation of the immune response.Journal of Theoretical Biology,1989,141(2):211–245.