Assessment and sequencing of air target threat based on intuitionistic fuzzy entropy and dynamic VIKOR

ZHANG Kun,KONG Weiren,LIU Peipei,SHI Jiao,LEI Yu,and ZOU Jie

1.School of Electronics and Information,Northwestern Polytechnical University,Xi’an 710072,China;2.Science and Technology on Electro-Optic Control Laboratory,Luoyang 471009,China

1.Introduction

Most moderncombat situationsare cluster combats,which require the pilots to face the enemy multi-target.According to the air combat situation,the enemy target threat is to make a reasonable assessment,and improve the operational efficiency of multi-target attack and self-survival probability.Therefore,it is practically significant to review the threat assessment[1,2].

Since Zadeh put forward the fuzzy set[3]and applied it to multiple attribute decision making,the fuzzy multiattribute problem has been developed rapidly.Intuitionistic fuzzy sets[4]were proposed by the Bulgarian scholar Atanassov in1986.On the basis of conventional fuzzy sets,a new attribute parameter-hesitation,the nonmember ship function is added which can describe the characterization of fuzzy nature more precisely[5].Nowadays,intuitionistic fuzzy sets have attracted much attention.As the air combat process is dynamic and continuous,using a static data description method for processing air combat threat assessment can lead to loss of information in air combat situations before the current time.It is difficult for a continuous air combat situation to make objective and comprehensive analysis,resulting in the greatly reduced rationality of the assessment.Finally,many scholars used the technique for order of preference by similarity to ideal solution(TOPSIS)method[6]for threat assessment.The basic principle of the TOPSIS method is that the chosen alternative should have the“shortest distance”from the ideal solution and the “farthest distance”from the “negativeideal”solution.The TOPSIS method introduces two “reference”points,but it does not consider the relative importance of the distances from these points.The TOPSIS method uses vector normalization to eliminate the units of criterion functions.The normalized value of the TOPSIS method depends on the evaluation unit of a criterion function.The VlseKriterijumska Optimizacija I Kompromisno Resenje(VIKOR)method[7–10]of compromise ranking determines a compromise solution,providing a maximum“group utility”for the “majority”and a minimum of individual regret for the “opponent”.The VIKOR method avoids the shortcomings of the TOPSIS method which has very strong superiority[11].

Therefore,assessment and sequencing of air target threat based on intuitionistic fuzzy entropy(IFE)[12–14]and dynamic VIKOR are proposed in this study.The target attribute weight is calculated by the IFE algorithm which aims at combat information uncertainty.Time series weight is gained by the poison distribution method which aims at high dynamic enemy operations.The dynamic VIKOR threat assessment method is carried out to attain the air combat hybrid formation.A multi-target threat assessment model is established to improve the sci-entific rationality of multi-target threat assessment for air combat.

2.Alternative attribute weight determine based on IFE

2.1 Preliminaries

We assume a finite set[15,16]of possible alternatives X={xi}(i=1,2,...,m),a finite set of attributes according to the desirability judgment of alternatives A={ai}(j=1,2,...,n),and the time sequence T={tk}(k=1,2,...,p).

Definition 1Let X be a finite universal set.An intuitionistic fuzzy set(IFS)A in X may be mathematically expressed as

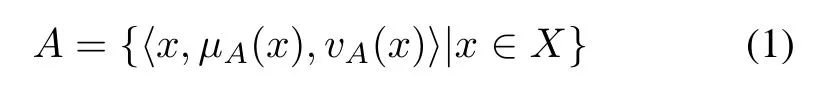
where the functions μA:X → [0,1]and νA:X → [0,1].

Membership and non-membership degrees of an element are defined as x∈X to A∈X,respectively,in such a way that they satisfy the condition:0≤ μA(x)+νA(x)≤1,for any x∈X.

Let γA(x)=1- μA(x)- νA(x),which is called the intuitionistic index of an element x in the IFS A.It is the degree of indeterminacy membership of the element x to A.Obviously 0≤γA(x)≤1.

If|A|=1,i.e.,there is only one element x in A,then the IFS A usually is denoted by A= 〈μA(x)-νA(x)?for short.

Definition 2Let A={〈x,μA(x),vA(x)?|x ∈ X}and B={〈x,μB(x),vB(x)?|x ∈ X}be two IFSs in the set X and λ≥0,then

(i)A+B={〈x,μA(x)+ μB(x)- μA(x)μB(x),vA(x)μB(x)?}

(ii)AB = {〈x,μA(x)μB(x),μA(x)+ μB(x)-μA(x)μB(x)?}

(iii)λA={〈x,1-(1- μA(x))λ,(μA(x))λ?}

(iv)Aλ={〈x,(μA(x))λ,1-(1- μA(x))λ?}.

2.2 Alternative attribute weight determination

The IFE method uses probability theory as a mathematical tool of metric information.Overcome the effects of uncertain information by intuition and ambiguity,and the full measure of uncertain information of IFS through the establishment of the entropy minimization nonlinear programming model for solving the calculation of attribute weights.The algorithm is as follows:

Step 1Construct the dynamic intuitionistic fuzzy decision matrix at time tk,as expressed in(2).

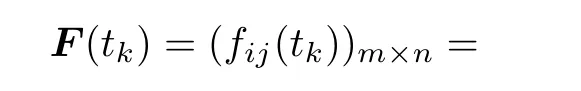
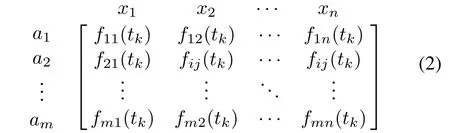
where fij(tk) = 〈μij(tk),νij(tk)?, μij(tk) ≥ 0,νij(tk) ≥ 0,and μij(tk)is the membership of alternative xiwith respect to attribute aiat the time tk,νij(tk)is the non-membership of alternative xiwith respect to attribute aiat the time tk.

Step 2Calculate IFE at the time tk,according to(3).

Step 3The alternative attribute weight nonlinear programming model is constructed as

where ωj(tk)is the weight for attribute aiat the time tk.

Step 4Compute the attribute weights:ω(tk) =(ω1(tk),ω2(tk),...,ωn(tk));and the Lagrange function is defined as(5).

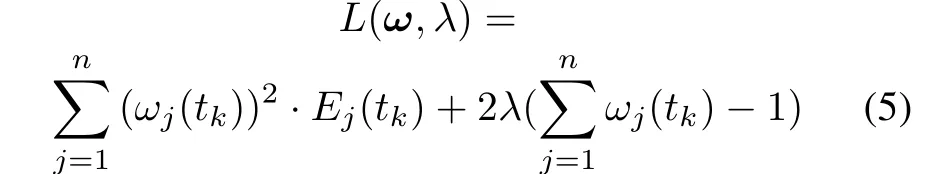
Compute the partial derivative of(5)with respect to each variable,

The attribute weight can be calculated as(7).

3.Dynamic VIKOR method in decision making process

3.1 Time series weight determination based on Poisson distribution method

Effect of different time points in air combat target data on threat assessment is not the same.Change of the air combat situation to make a comprehensive and objective assessment must be a different time point of time series empowerment.The actual combat process is closer at the moment and collected information of target threat assessment is more important.In this study,the weight of time series is calculated by an inverse form of the Poisson distribution.η=(η1,η2,...,ηp),

3.2 Dynamic VIKOR method in decision making process based on time series weight

Based on attribute weight and time series weight,the method is presented in a step by step algorithm as follows:

Step 1Construct the dynamic intuitionistic fuzzy decision matrixF(tk)by(2).

Step 2Construct the weighted intuitionistic fuzzy decision matrixZ;

Step 3Determine the positive ideal solution(PIS)and negativeideal solution(NIS)of weighted intuitionistic fuzzy decision matrixZ.

The PIS is given by

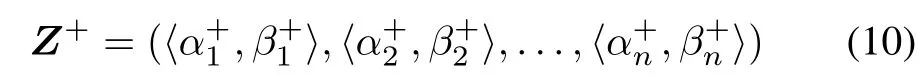
The NIS is given by

Step 4Compute Si,Ri,Qi.

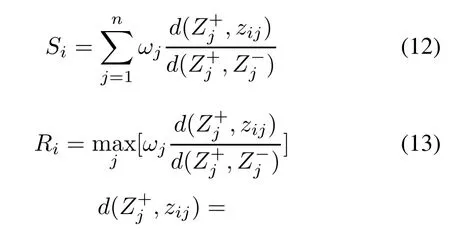
where Siis the maximizing group effect,it is the weighted Hamming distance between the evaluation value of the ith scheme and the ideal solution.Riis the minimizing individual regret,it is the weighted Chebyshev distance between the evaluation value of the ith scheme and the negative ideal solution.ωjis the weight of each evaluation criterion.υ is the decision-making mechanism coefficient.Step 5Sequence the alternatives according to the relations of Si,Ri,Qi.The smaller the value is,the better the corresponding alternatives are.

4.Numerical examples and discussion

We assume that we encounter four enemy aircraft in combat and each enemy’s plane has four attributes.Its objective information is to select the current and previous two times sample data.The information is presented in Table 1.

Table 1 Target data information

According to(7),the attribute weight is shown as follows:

ω(t1)=(0.265 4,0.219 0,0.168 4,0.347 2)ω(t2)=(0.263 3,0.206 4,0.249 9,0.280 4)ω(t3)=(0.325 4,0.215 8,0.234 1,0.224 7).

According to(8),the time series weight is shown as follows when φ=1.5:

η=(0.200 0,0.266 7,0.533 3).

According to(10)and(11),the PIS and NIS are given as follows:

According to(12)–(14),set υ =0.5,we can calculate the results as follows:

Finally,the most threatening target is m1,the optimal sequencing result is given by m1＞m3＞m4＞m2.By comparing the proposed methods,the TOPSIS method is utilized in assessing the air threat by the same assumption.The TOPSIS method was firstly developed by Hwang and Yoon in 1981.The basic approach of this method is choosing an alternative that should have the shortest distance from the positive ideal solution and the farthest distance from the negative ideal solution.The positive ideal solution maximizes the benefit criteria and the minimizes conflicting criteria.However,the negative ideal solution maximizes the conflicting criteria and minimizes the benefit criteria.This method has been applied in many combat threat assessment problems.The rationality of this method has been proved by many combat examples.The assessment results which are calculated by the TOPSIS method are 0.586 0,0.448 5,0.581 5,0.571 7 in 0.036 2 s.The sequencing result is m1＞m3＞m4＞m2.The result of two methods is the same.And the result is consistent with the method which is proposed by this study[17].We conclude that the threat assessment result is rational and effective.

Moreover,the method has some advantages compared with the TOPSIS method.Dynamic character and flexible parameter υ are the obvious characteristics of the proposed method.The assessment and sequencing results of different υ are presented in Table 2.

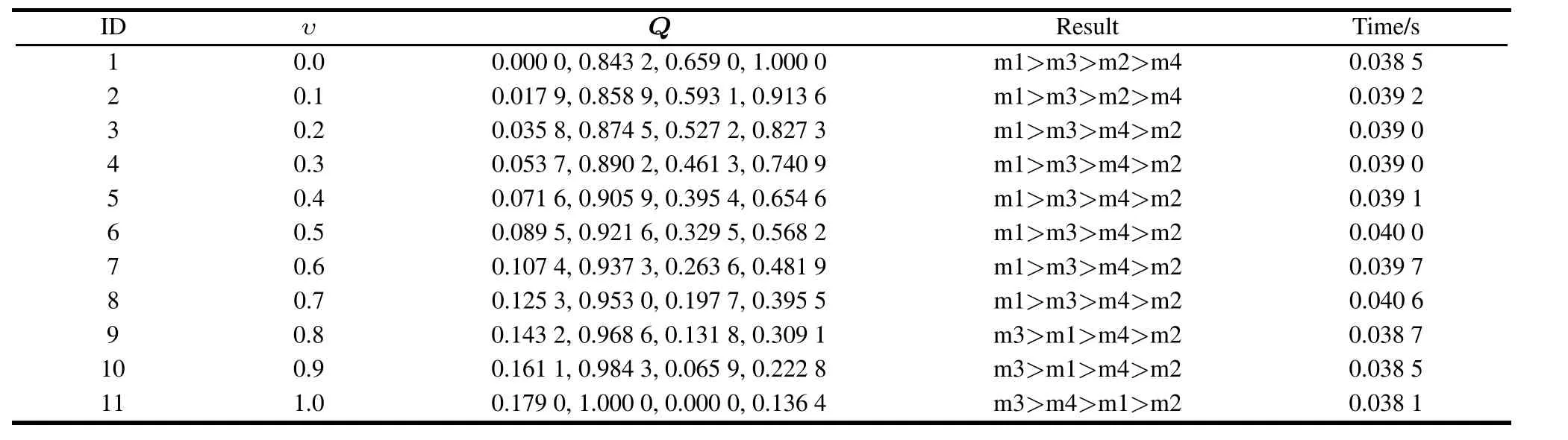
Table 2 Results of different υ

We use modified VIKOR assessment result(1-Q)in order to facilitate comparison and display the results in Fig.1.

Fig.1 shows that results change when we use different υ values.In the first group υ =0.0-0.1,the sequencing result is m1＞m3＞m2＞m4.In the second group υ =0.2-0.7,the sequencing result is m1＞m3＞m4＞m2.In the third group υ=0.8-0.9,the sequencing result is m3＞m1＞m4＞m2.While in the fourth group υ =1,the sequencing result is m3＞m4＞m1＞m2.

We conclude that,the threat level superimposed when targets 3 and 4 consider all of the threat attributes,has a beyond tendency.The threat degree of target 3 exceeds target 1 when υ=0.8;the threat degree of target 4 exceeds target 2 when υ=0.2;the threat degree of target 4 exceeds target 1 when υ=1.0.Targets 1 and 2 have the threat degree when considering the single attribute.However,they have a lower threat degree when considering all of the threat attributes.The results based on the TOPSIS method are consistent with the results based on VIKOR when υ=0.2-0.7,which is in line with the results of most sorting.Calculation time is given in Table 2.We also conclude that,all the calculation time of different methods is about 0.038–0.040 s with the maximum time difference of 0.001 9 s with similar efficiency.

The VIKOR method can be layered between individual attributes and all attributes,for example,in the combat threat assessment process,if the enemy has airborne warning and control system(AWACS),which has lower maneuvering ability but higher battle field situation control ability.The new threat level can be implemented by the VIKOR method while the TOPSIS method is incapable of action.At the same time,we can see that the result computed by TOPSIS is very close,it can cause various threats of almost all illusions.However,in order to facilitate the process of air combat prompt pilots through the VIKOR method,it can be more significant to reflect the extent of the differences between the various threats.

Fig.1 Result figures

Using the same simulation parameters,the simulation data do not change at time T3.At time T2,target 4 accelerates motion value changed from 〈0.73,0.19?to 〈0.80,0.15?.The result is 0.0636,0.9689,0.7305,0.5000 when υ =0.5.The sequencing result is m1＞m4＞m3＞m2.In this study,the dynamic process of the combat situation and threat assessment is combined.When target 4 has a tendency to accelerate the movement,raise the threat level to get a more reasonable assessment of the threat.

5.Conclusions

The modern combat process is always an uncertain,dynamic and hybrid formation.Considering that the traditional air target threat assessment methods are difficult to reflect the combat characteristics,an algorithm is proposed to solve the multi-target threat assessment problems.The target attribute weight is calculated by the IFE algorithm and the time series weight is gained by the Poisson distribution method based on multi-times data.Assessment and sequencing of the air multi-target threat model based on IFE and dynamic VIKOR are established.Finally,a simulation example indicates that the method is reasonable and effective.And this method improves the scientific rationality of multi-target threat assessment for air combat.

[1]ZHANG C K,ZHU Z X,FENG Q,et al,Visualization threat assessment for air combat based on interval-radar chart.Systems Engineering and Electronics,2016,38(5):1052–1058.(in Chinese)

[2]XU Y,WANG Y,MIU X.Multi-attribute decision making method for air target threat evaluation based on intuitionistic fuzzy sets.Journal of Systems Engineering and Electronics,2012,23(6):891–897.

[3]ZADEH L A.Fuzzy sets.Information and Computation,1965,8(3):338–353.

[4]ATANASSOV K T.Intuitionistic fuzzy sets.Fuzzy Sets and Systems,1986,20(1):87–96.

[5]XU Z,ZHAO N.Information fusion for intuitionistic fuzzy decision making:an overview.Information Fusion,2016,28(C):10–23.

[8]TAVANA M,KIANI R,MAVI F J,et al.An extended VIKOR method using stochastic data and subjective judgments.Computers&Industrial Engineering,2016,97(1):240–247.

[9]JIANG W Q.Risky fuzzy multi-criteria decision method based on prospect theory and VIKOR.Control and Decision,2014,29(12):2287–2291.

[10]JIANG W Q.Extension of VIKOR method for multi-criteria group decision making problems with triangular fuzzy numbers.Control and Decision,2015,30(6):1059–1064.

[11]AGHAJANI MIR M,TAHEREI GHAZVINEI P,SULAIMAN N M N,et al.Application of TOPSIS and VIKOR improved versions in a multi criteria decision analysis to develop an optimized municipal solid waste management model.Journal of Environmental Management,2016,166(9):109–115.

[12]CHANGKH,CHENGCR.Application of intuitionistic fuzzy entropy to disruption risk management in aerospace supply chain.Applied Mathematics&Information Sciences,2016,10(3):1035–1046.

[13]JAHAN A,MUSTAPHA F,ISMAIL M Y,et al.A comprehensive VIKOR method for material selection.Materials&Design,2011,32(3):1215–1221.

[14]SZMIDT E,KACPRZYK J.Entropy for intuitionistic fuzzy sets.Fuzzy Sets and Systems,2001,118(3):467–477.

[15]CHENZ,XIONGS,LIY,et al.Entropy measures of type-2 intuitionistic fuzzy sets and type-2 triangular intuitionistic trapezodial fuzzy sets.Journal of Systems Engineering and Electronics,2015,26(4):774–793.

[16]FAN X S,LEI Y J,LI C H,et al.Strict intuitionistic fuzzy entropy.Systems Engineering and Electronics,2016,38(3):602–606.(in Chinese)

[17]ZHANG K,WANG X,ZHANG C K,et al.Evaluating and sequencing of air target threat based on IFE and dynamic intuitionistic fuzzy sets.Systems Engineering and Electronics,2014,36(3):74–78.(in Chinese)