铁路专用线平交道口碰撞危险性分析

石红国，饶 煜，罗 望，张 鹏

SHI Hong-guo, RAO Yu, LUO Wang, ZHANG Peng

（西南交通大学 交通运输与物流学院，四川 成都 610031）

(School of Transportation and Logistics， Southwest Jiaotong University， Chengdu 610031， Sichuan， China)

随着我国经济的快速发展，铁路列车运行速度加快、运行密度增加，无形中增加了铁路专用线平交道口的危险性。由于铁路专用线平交道口大多处于无人看守状态，因而存在着极大的安全隐患[1]。为此，通过分析影响铁路专用线平交道口碰撞事故发生的因素[2]，建立铁路专用线平交道口碰撞概率模型，计算汽车与列车碰撞发生概率及碰撞后所导致的经济损失，最终根据碰撞概率和碰撞经济损失得出一年内铁路专用线平交道口的期望经济损失，为评估铁路专用线平交道口危险性提供理论基础。

1 铁路专用线平交道口碰撞概率模型构建及经济损失计算

1.1 碰撞概率模型构建

我国铁路专用线无人看守的平交道口数量众多，一般情况下，铁路受到列车的牵引质量、运行速度等因素影响，列车制动距离一般比较长[3]。列车通过道口时机车乘务员主要采用加强瞭望、鸣笛等较为被动的方式避免事故发生。而汽车由于制动距离相对较短，在通过道口时汽车司机只需要加强瞭望，及时减速停车，避免在通过无人道口时发生碰撞事故。因此，构建铁路专用线平交道口碰撞概率模型，主要从汽车的角度计算铁路专用线平交道口碰撞概率。

无人看守道口事故可以分为以下 3 类情况：①汽车司机事先没有发现列车通过或接近道口，与列车相撞；②汽车司机已经发现有列车接近道口，抢道时与列车相撞；③由于道口的坡度、路面情况等因素造成汽车在道口熄火，与列车相撞。第 2 种情况受人的主观因素影响较大，第 3 种情况发生较为偶然，因而重点讨论第 1 种情况。

铁路专用线平交道口列车与汽车碰撞示意图如图 1 所示。假设列车速度为V1，列车长度为L1，列车宽度为D1，汽车速度为V2，汽车长度为L2，汽车单侧瞭望距离为S1，汽车紧急制动距离为S2。假设图 1 中列车从左向右行驶，汽车从下向上行驶。如果汽车司机首次发现有列车接近时，汽车所处位置在点D以后的区间DF内，则汽车可以在距离道口还有若干米的距离停止，此时一定不会发生碰撞事故，因而以点D作为分界点讨论汽车与列车相撞的概率。

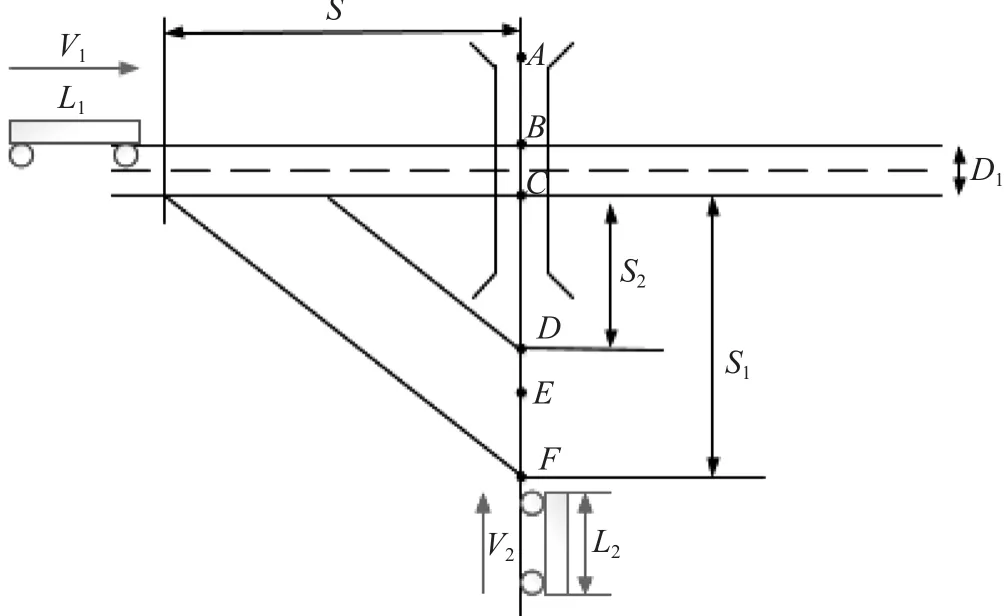
图 1 铁路专用线平交道口列车与汽车碰撞示意图Fig.1 The diagram of Collision between the trains and vehicles on Grade Crossing of Industrial Siding

假设汽车司机由汽车从点F行驶至点D这段时间内没有发现列车。在这种情况下对于一辆匀速行驶至D点的汽车而言，此时列车有 3 种状态：一是列车已经通过道口；二是列车正在通过道口；三是列车尚未通过道口。在第 1 种状态下列车与汽车不可能相撞，因而主要分析第 2、第 3 种状态下的碰撞概率。

（1）在第 2 种状态下，列车通过道口时在汽车司机视线的正前方，假设列车在汽车到达D点之前的t时间到达道口，意味着汽车司机在到达D点的前T1(T1＞t) 时间内疏忽，完全没看前方，才可能导致汽车继续以匀速行驶至D点。汽车行驶至D点时列车通过道口的剩余时间为t1，则有

汽车由D点紧急制动至道口的时间为t2，由速度位移公式可得

如果t1＞t2，则汽车必定撞上列车。考虑到汽车司机开车时因疏忽而没有目视前方的时间T1较短，而t＜T1，可以认为此时t1必然大于t2，从而可以得出结论：假设汽车司机疏忽的时间为T1，则在汽车司机开小差行驶至D点 (开小差之前没有瞭望) 的前T1时间内有列车到达道口，则碰撞事故一定发生。

在图 1 中，假设汽车司机于E点疏忽，假设汽车司机在EF区域内不瞭望的概率为PEF，T1时间内汽车司机开小差的概率为PDE，T1时间内有列车到达道口的概率为PT1，则汽车司机事先没有发现列车正在通过道口而发生碰撞的概率P1为

（2）在第 3 种状态下，假设L1/V1＞S2/V2，即列车占用道口的时间大于汽车在紧急制动距离S2内行驶的时间，该假设是为避免当汽车行驶于S2距离内时，列车已经通过道口的情况发生，这与实际情况相符。此后，当汽车行驶于区间BD中任意位置时，如果有列车到达道口则必定发生碰撞事故。假设汽车由头部进入D点至尾部驶出B点所需最短的时间为T2。T2应为汽车由头部进入D点起就开始加速行驶，至尾部驶出B点所耗费的时间。由于区间BD的长度较短，汽车行驶速度较高且汽车的重量、加速度未知，汽车加速通过区间BD耗费的时间与汽车匀速通过区间BD的时间差别比较小，在计算时令T2近似等于汽车匀速通过区间BD所耗费的时间，则有

由此可知，当汽车在事先没有瞭望的情况下以速度V2行驶至D点后的T2秒内，如果有列车到达道口，此时汽车处于或部分处于区间BD中，则碰撞事故一定发生。

假设汽车司机在DF区域内不瞭望的概率为PDF，T2时间内有列车到达道口的概率为PT2，则汽车司机事先没有发现列车接近道口而发生碰撞的概率P2为

结合以上分析，汽车司机事先没有发现列车通过或接近，与列车相撞的概率P为

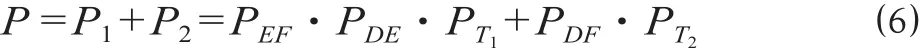
（3）针对PT1，PT2，PDF，PEF，PDE，P的概率计算，假设 1 天即 86 400 s 内有N1趟列车从左往右经过道口，则每秒钟到达的列车数为λ，计算公式为

假设t时间内列车到达道口的次数服从泊松分布，显然这不完全符合事实，因为列车运行存在间隔时间T，即T时间内 2 趟以上列车到达的概率为0，但考虑到λT1和λT2值特别小，按照泊松分布计算出的λT1和λT2时间内 2 趟以上列车到达的概率几乎为 0，所以这种假设还是可以接受，则有

假设汽车司机每秒钟瞭望道路两边的次数为α，显然α的取值与汽车司机身处的环境及汽车司机的心理有关。假设t时间内汽车司机瞭望的次数x服从泊松分布，则汽车从点F行驶至点D这段时间内，汽车司机没有瞭望的概率PDF=P(x= 0)，则有

式中：t3为汽车在区域DF内行驶的时间。t3的计算公式为

汽车从点F行驶至点E这段时间内，汽车司机没有瞭望的概率PEF=P(x= 0)，则有

式中：t4为汽车在区域EF内行驶的时间。t4的计算公式如下。

假设汽车司机每秒钟注视道路前方的次数为β，并假设t时间内汽车司机注视前方的次数x服从泊松分布，则T1时间内司机疏忽等同于T1时间内司机注视前方的次数为 0，则有

由公式 ⑹ 至公式 ⒁ 可得

以上讨论是在列车从左向右行驶，汽车从下往上行驶的情况下，汽车司机事先没有发现列车通过或接近时，可能发生事故的概率。考虑到列车也有可能是从右向左驶来，此时假设汽车司机对道路两边的瞭望距离相等，并且假设列车上下行开行列车数相等，此时事故发生的概率应为

（4）针对铁路专用线平交道口碰撞事故期望次数计算，假定一年内双方向通过道口的汽车数为N2，并且假定双方向的瞭望条件、汽车司机每秒钟瞭望道路两边的次数、列车上下行车流量都相等，则一年内由于汽车司机没有发现列车通过或接近而可能发生的道口事故次数N为

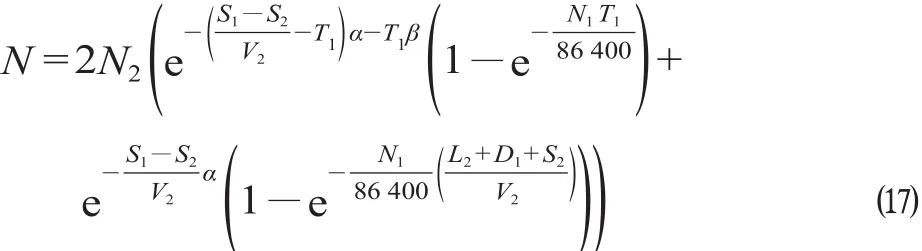
汽车的制动距离S2与汽车的速度有关[1]，一般可取

将公式 ⒄—⒇ 化简得出一年内因汽车司机没有发现列车通过或接近而发生的道口事故期望次数N为

分析公式 (21) 可知，在汽车、列车的流量一定时，道口的瞭望条件 (包括瞭望距离、影响司机警觉性的各种因素等) 对道口事故的发生影响很大，客观决定了道口事故发生的期望次数。

1.2 碰撞事故经济损失计算

铁路专用线平交道口碰撞事故的经济损失是由直接经济损失和间接经济损失所构成[4]。碰撞事故的直接经济损失费用由财产直接损失和人员伤亡直接损失构成，间接经济损失主要包括运输能力下降间接损失和车辆占用间接损失。铁路专用线平交道口碰撞事故经济损失构成如图 2 所示。

（1）铁路专用线平交道口碰撞事故直接损失费用计算包括财产直接损失和人员伤亡直接损失，可以通过有关部门和相关的法律条文直接统计出来。

（2）铁路专用线平交道口碰撞事故间接损失费用计算包括运输能力下降间接损失，可以根据列车密度和中断行车时间计算出中断的列车数量，再通过列车的平均载重数计算出被影响的货物周转量，从而计算出运输能力下降间接损失。因此，运输能力下降间接损失的计算公式为

式中：M为列车密度，是线路区间一昼夜实际通过的列车数量，列；T中断为中断时间，h；Z为列车所装载的货物质量，t；V列为列车行驶的平均速度，km/h；Lt为每“吨公里”的收入，元/(t · km)。

车辆占用导致的间接损失是指由于道口事故造成编组站待发列车不能正常发出和在途列车晚点，从而导致车辆被占用却不能产生经济效益的情况，可以用下式计算。

式中：N列为事故造成编组站待发和在途列车总数，列；S为货物列车平均编组辆数，辆；T晚点为列车平均晚点时间，h；L车日为列车车辆由于非生产因素而被占用一日 (简称“一个车日”) 所造成的经济效益损失费用，元。

图 2 铁路专用线平交道口碰撞事故经济损失构成Fig.2 The component parts of economic losses about grade crossing of industrial siding

2 实例分析

2.1 郭白铁路专用线道口概况

郭白铁路 (郭尔奔敖包—白音芒来) 位于内蒙古锡林郭勒盟境内，西起集二线的郭尔奔敖包站，沿既有郭查支线 (郭尔奔敖包—查干诺尔) 至乌日根塔拉站后向东北方向引出，终至苏尼特左旗境内的白音乌拉煤田芒来煤矿，服务于新建的年产量 3 500 万 t大型露天矿外运。线路全长 141.7 km，列车运行密度大，线路沿线有多个无人看守的平交道口，存在一定风险，其中一道口由于受地形条件限制，汽车行驶在道路上的瞭望距离为 300 m，并且道路与铁路线路的夹角为 90°，具有一定的代表性。因此，以该道口为例，运用上述理论方法，对该道口进行危险度指标计算。

2.2 碰撞事故发生概率及经济损失计算参数

（1）列车相关的参数。郭白铁路专用线列车运行密度为 32 对/d；货物列车运行速度为 70 km/h；货物列车行驶的平均速度为 45 km/h；货物列车编组辆数为 50 辆；列车车辆静载重为 60 t；货物列车车长 641 m；列车车体宽度为 2.8 m。

（2）汽车相关的参数。每天通过道口的卡车数为 450 辆；每天通过的越野车数为 200 辆；运煤卡车车长 8 m；运煤卡车行驶速度为 36 km/h；越野车车长 5 m；皮卡车行驶速度为 64.8 km/h；瞭望距离为 300 m。

（3）经济损失计算所需参数。铁路行车中断时间为 4 h；与空车相撞直接经济损失为 350 万元；与重车相撞直接经济损失为 500 万元；每吨公里的收入率为 0.15 元/(t · km)；事故造成编组站待发和在途列车总数为 9 列；列车平均晚点时间为 3 h；车辆一个车日费用为 500 元。

2.3 期望经济损失计算

经过对现场的实地调研可知，通过该平交道口的汽车类型主要有大卡车 (运煤) 和越野车 2 类。大卡车和越野车在道路上行驶的速度和车长均不相等，因而它们与货物列车相撞的概率也不一样，应分别计算各自的碰撞概率。

郭白铁路专用线是单线区段，列车运行方向有重车方向和空车方向，并且汽车与重车方向的货物列车相撞所造成的经济损失比汽车与空车方向的货物列车相撞所造成的经济损失大，因而计算期望经济损失时按照汽车 (分越野车和大卡车) 与重车相撞和汽车与空车相撞 2 种情况来计算。

一年内大卡车与重车相撞的期望次数为

一年内越野车与重车相撞的期望次数为

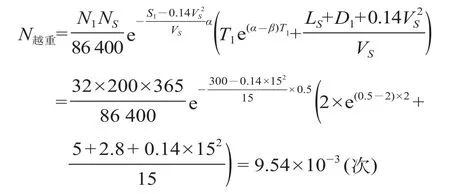
式中：Ls为越野车的车长；Vs为越野车的速度。

因此，一年内汽车与重车方向列车相碰撞的期望次数为

假设空车方向的列车列数与重车方向货物列车数相等，并且列车运行速度相等，显然这是符合实际的，则一年内汽车与空车方向列车相碰撞的期望次数为

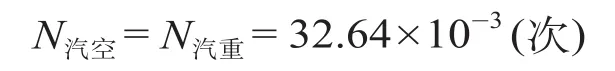
假设大卡车、越野车与列车碰撞所导致的经济损失一样，下面计算汽车和重车碰撞一次的经济损失，汽车与空车相撞一次的经济损失可以通过折算系数γ与汽车和重车相撞的经济损失相乘得出。

直接损失费用：W直损= 500 (万元)

根据上述公式及相关参数进行间接损失费用计算如下。

因此，汽车与重车碰撞一次的间接损失费用为

W间损=W1+W2= 43.2 + 2.8 = 46 (万元)

W损=W直损+W间损= 500 + 46 = 546 (万元)

查阅相关文献可知，汽车与空车相撞的经济损失相对于汽车与重车相撞的经济损失其折算系数取值为 0.7。因此，一年内铁路专用线平交道口发生事故的期望经济损失为

W期损=W损N汽重+γW损N汽重=W损(1 +γ)N汽重

W期损= 546×(1 + 0.7)×0.032 64 = 30.30 (万元)

经过以上分析可知，郭白铁路专用线平交道口碰撞事故期望经济损失为 30.30 万元，作为铁路专用线危险度指标，其经济损失较高，危险度较大，严重威胁铁路专用线的安全运行，相关部门应采取有效的措施提高平交道口的安全性，保障郭白铁路专用线健康高效运营。

3 结束语

一般对铁路专用线平交道口碰撞危险性分析大多局限于导致碰撞事故发生因素的定性研究[5-8]。为此，在既有研究的基础上，将铁路专用线平交道口碰撞事故期望经济损失作为铁路专用线危害度指标用以定量评估铁路专用线平交道口安全水平，为铁路专用线平交道口的安全评估提供新的方法，可以有效提高铁路专用线平交道口的安全管理水平。

参考文献：

[1]王寄存，刘英伟，严 川. 铁路运输安全评价体系研究[J]. 铁道货运，2006，24(12)：21-24.WANG Ji-cun，LIU Ying-wei，YAN Chuan. Research on Safety Evaluation System of Railway Transportation[J].Railway Freight Transport，2006，24(12)：21-24.

[2]ANANDARAO S，MARTLAND C D. Level Crossing Safety on East Japan Railway Company：Application of Probabilistic Risk Assessmenttechniques[J]. Transportation，1998，25(3)：265-286.

[3]郭寒英，石红国，张 鹏，等. 基于动态模糊理论的铁路专用线安全评价[J].铁道运输与经济，2017，39(2)：40-45.GUO Han-ying，SHI Hong-guo，ZHANG Peng，et al.Safety Evaluation of Railway Industrial Sidings based on Dynamic Fuzzy Theory[J]. Railway Transport and Economy，2017，39(2)：40-45.

[4]刘 东，路 峰. 道路交通安全管理规划体系初探[J]. 中国安全科学学报，2004，14(5)：51-54.LIU Dong，LU Feng. Preliminary Study on the Road Traffic Safety Programming System[J]. China Safety Science Journal，2004，14(5)：51-54.

[5]李家稳，张海燕，施仲衡，等. 铁路道口安全与框构桥设计软件实现[J]. 中国安全科学学报，2003，13(10)：48-51.LI Jia-wen，ZHANG Hai-yan，SHI Zhong-heng，et al.Safety of Railway Crossing and Software Realization in the Design of Frame Bridge[J]. China Safety Science Journal，2003，13(10)：48-51.

[6]张殿业，金 键，郭孜政. 道路交通事故预防研究体系探讨[J]. 中国安全科学学报，2007，17(7)：132-138.ZHANG Dian-ye，JIN Jian，GUO Zi-zheng. Exploration into Road Traffic Accident Prevention Research System[J].China Safety Science Journal，2007，17(7)：132-138.

[7]武新宇. 道口事故分析及对策[J]. 中国铁路，2004 (12)：53-54.WU Xin-yu. Analysis and Countermeasures of Crossing Accident[J]. Chinese Railways，2004(12)：53-54.

[8]贾明涛，王海星，肖贵平. 铁路道口安全影响因素分析及对策[J]. 安全与环境学报，2006，6(6)：123-126.JIA Ming-tao，WANG Hai-xing，XIAO Gui-ping. Analysis and Countermeasures of Safety Influence Factors of Railway Crossing[J]. Journal of Safety and Environment，2006，6(6)：123-126.