DDA法抛物线插补运算研究
2018-04-26李双成陈兴媚
李双成,陈兴媚
(广东理工学院 工业自动化系,广东 肇庆 526100)
DDA法又称数字积分法,该方法具有运算速度快,能够实现多次方曲线插补、多坐标轴联动控制、脉冲分布均匀及较高的插补精度等优点,因此广泛应用于各种数控轮廓控制系统中。
1 DDA法插补基本原理

当Δt取1个脉冲当量“1”时,有:


图1 DDA法几何描述
2 DDA法在抛物线加工中的运算分析
2.1 DDA法抛物线插补积分表达式推导
在抛物线加工过程中,可以效仿DDA法圆弧插补的方法,找到DDA法抛物线插补积分表达式及抛物线插补器结构框图。假设编程轮廓为逆时针开口向上抛物线(见图2),该抛物线起点坐标为A(x0,y0),刀具动点坐标为B(xi,yi),终点坐标为E(xe,ye),则抛物线的标准方程为:x2=2py。两边微分,整理得:
由:
得:
令:
则:
vx=pk
vy=xk
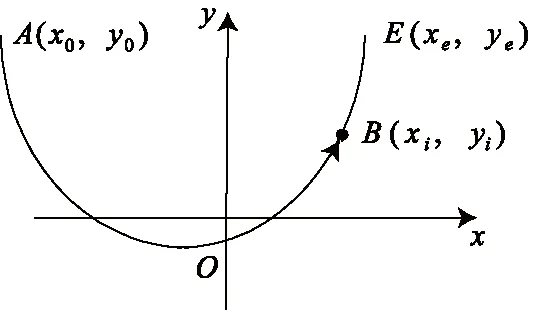
图2 开口向上逆时针抛物线
假设经过n次累加后,x轴和y轴分别(或同时)到达终点E(xe,ye),则可得DDA法抛物线插补积分表达式为:
令Δt=1,k=1/2N则:
(1)
(2)
式中,k为比例常数;2N为积分累加器容量;N为累加器、寄存器的位数。由式1、式2可知,DDA法抛物线插补是对动点B(xi,yi)从起点走向终点过程中,各坐标轴每经过1个单位时间间隔Δt=1,分别以增量p和xi同时累加的过程,若累加器产生溢出,则在相应坐标方向进给一步。
2.2 DDA法抛物线插补器结构框图构建
与DDA法圆弧插补类似,也可用2套数字积分器,根据式1和式2构成抛物线插补结构框图。开口向上逆时针抛物线插补器结构框图如图3所示,图3中,JVx、JVy为x、y被积函数寄存器,抛物线插补时,JVx中存放抛物线焦点到准线距离p为不变量;JVy中存放抛物线x轴动点坐标为一变量,随着插补过程的进行要及时修正JVy中的数据。对于图3来说,插补开始JVy中存放起点坐标值x0,当Δx(x坐标轴溢出脉冲)溢出1个脉冲时,要在JVy中“+1”;反之,JVy中数据不变。JRx、JRy为积分累加器,当脉冲源发出1个控制脉冲信号Δt,则x、y积分累加器各累加1次,当累加结果超出JRx和JRy容量(2N)时,就溢出1个脉冲Δx(或Δy),这样经过(2N)次累加后,每个坐标轴的输出脉冲总数就等于该坐标的终点函数值xe和ye,从而控制刀具到达终点E(xe,ye)[1-2]。

图3 开口向上逆时针抛物线插补器结构框图
2.3 终点判别
DDA法抛物线插补时,由于各坐标轴的方向不同,且到达终点的时间也不一定相同,因此应分别判断x、y坐标轴进给步数。可以利用2个终点减法计数器J∑x=|xe-x0|和J∑y=|ye-y0|来实现,把x、y坐标所需输出脉冲数|xe-x0|、|ye-y0|分别存入2个减法计数器中,当某一坐标轴每输出1个脉冲时相应计数器减1,当其减到0时说明该坐标轴已插补到终点,该坐标轴即停止累加运算;只有当两计数器均为0时才停止抛物线插补计算。
以上是关于y轴正半轴对称开口向上逆时针DDA法抛物线插补计算公式推导及结构框图的构建。式1、式2也适用于顺时针抛物线插补(见图4),同时需要重新构建插补结构框图(见图5)。
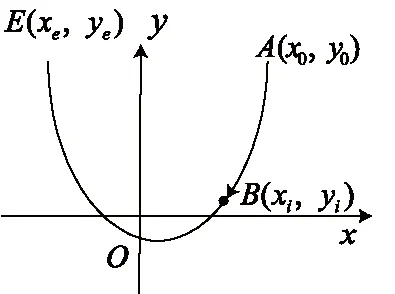
图4 开口向上顺时针抛物线图

图5 开口向上顺时针抛物线插补器结构框图
3 不同开口及不同象限抛物线插补脉冲分配
根据以上推导思想,可以将其推广至抛物线的不同开口、不同象限及不同加工方向(顺时针或逆时针)的DDA法插补运算中去。它们都有一个共同点,就是都在做JV+JR→JR求和运算,即累加的方式均一样,只是某个坐标轴的被积函数JVx或JVy进行“+1”修正或“-1”修正,以及溢出脉冲Δx、Δy进给方向的正负不同而已[3-8]。各种情况下脉冲分配及各坐标轴的进给方向见表1~表4。其中,SR表示顺时针插补抛物线,NR表示逆时针插补抛物线,下标1、2、3、4分别表示所在的象限。

表1 关于y正半轴对称顺、逆抛物线(开口向上) DDA法插补进给方向及相应坐标修正符号表
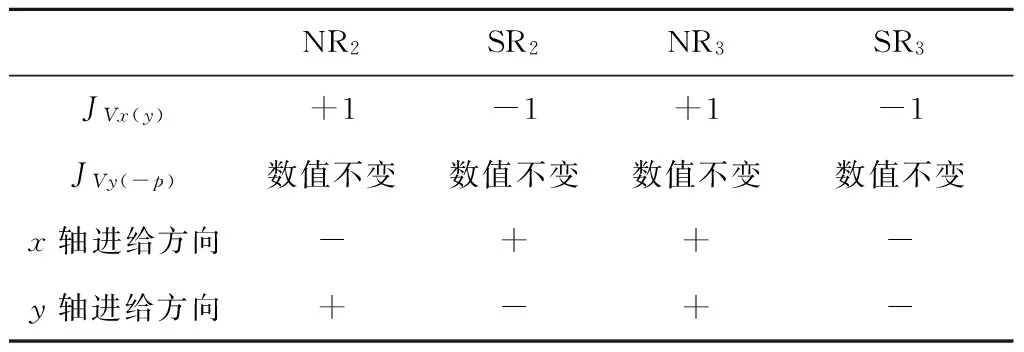
表2 关于x负半轴对称顺、逆抛物线(开口向左) DDA法插补进给方向及相应坐标修正符号表

表3 关于y负半轴对称顺、逆抛物线(开口向下) DDA法插补进给方向及相应坐标修正符号表
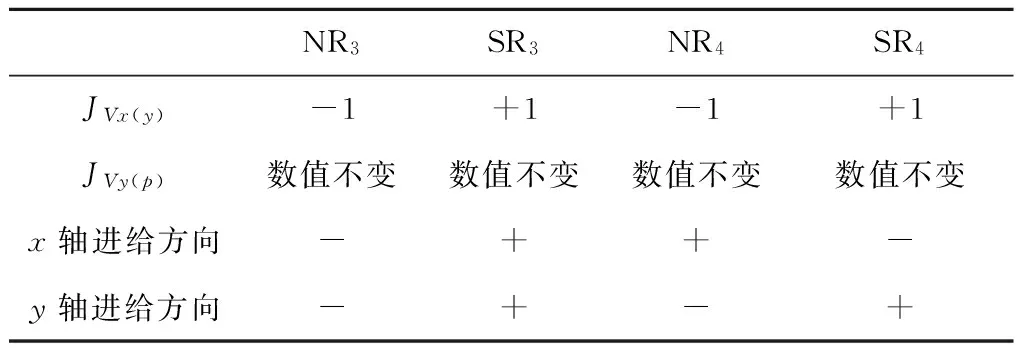
表4 关于x正半轴对称顺、逆抛物线(开口向右) DDA法插补进给方向及相应坐标修正符号表
4 DDA法抛物线插补举例
采用DDA法插补抛物线轨迹图如图6所示。设第1象限逆时针抛物线x2=2py,抛物线起点为O(0,0),终点为E(4,6),抛物线焦点到准线距离p=1,设寄存器位数N=3,应用DDA法进行抛物线插补。

图6 DDA抛物线插补轨迹
从前面插补公式推导可知,开始时,被积函数JVx=p=1,JVy=0;寄存器容量为2N=23=8,即寄存器满8,则Δx或Δy溢出1;每个坐标溢出1的总个数就是刀具在该坐标轴插补所走的刀数;终点计数器J∑x=|xe-x0|=|4-0|=4,J∑y=|ye-y0|=|6-0|=6。插补过程见表5。

表5 第1象限开口向上逆时针DDA法抛物线插补运算过程
5 结语
本文系统性地推导和总结了DDA法插补抛物线的积分函数运算及插补结构框图的构建,并将其拓展到4种不同开口方向及顺、逆抛物线的插补中;同时还给出了不同情况下各坐标轴的进给方向,为数控机床插补复杂曲线运算研究及应用提供了理论依据。
[1] 朱春晓,吴祥,任皓.数控技术[M].2版.北京:机械工业出版社,2006.
[2] 张建钢,胡大泽.数控技术[M].武汉:华中科技大学出版社,2000.
[3] 陈富安,赵渭平.数控机床原理与系统[M].2版.北京:人民邮电出版社,2011.
[4] 王润孝,秦现生.机床数控原理与系统[M]. 西安:西北工业大学出版社,2004.
[5] 胡赤兵,操良伟,闫琳.一种椭圆插补的改进算法[J].兰州理工大学学报,2007(6):33-35.
[6] 王爱玲, 张吉堂, 吴雁.现代数控原理及控制系统[M].北京:国防工业出版社,2005.
[7] 刘晓玲,齐庆国.数控机床[M].北京:冶金工业出版社,2014.
[8] 林宋,张超英,陈世乐.现代数控机床[M].北京:化学工业出版社,2011.
