基于贝叶斯最大似然估计的金融预测

沈 斌，温 涛

（西南大学a.数学与统计学院；b.经济管理学院，重庆 北碚 400715）

0 引言

金融预测是指对金融产品的历史数据，运用数据预测方法来预测其未来的市场价格和市场行为，其预测分析对象包括各类金融证券指标和金融产品价格，如各种利率、汇率和股票指数等。

金融预测模型一直是学者重点关注的领域，学者们从不同方面建立了不同的金融预测模型。近年来，伴随着我国金融业的快速发展，新金融产品逐渐出现，为了有效地掌握金融产品的市场发展规律，必须对金融产品发展趋势进行有效预测，相关研究者提出了不同的金融预测方法，从简单的单项预测方法，到逐渐发展起来的组合预测方法。单项预测方法主要包括传统的时间序列分析方法[1,2]、神经网络方法[3,4]等，这些单项预测方法的预测精度往往具有时好时坏性，而组合预测模型，尤其是变权重组合预测模型的预测效果往往更好。

组合预测模型的好坏，主要看预测值与实际值的拟合度大小。定常权预测模型类似于线性回归模型或线性规划模型，而变权组合预测模型类似于非线性规划模型。为了实现变权重的目的，在借鉴以往各期预测精度的基础上确定最优权重是一个比较好的选择，因此，有必要借鉴引导算子和最大似然理论。

以往论文关于最优化问题的设定，往往借助于最小二乘法构建优化模型，而诱导算子的设定往往只是考虑本期的预测精度[5-11]。在本文中，将运用贝叶斯最大似然理论构建诱导算子，运用灰关联理论构建优化模型，运用泰勒级数展开进行参数的等价转换，在此基础上，建立新的基于贝叶斯最大似然估计的组合预测模型，通过算例分析发现，当样本数据较大时，本组合预测方法具有较好的预测效果。在本文中，将研究基于贝叶斯最大似然估计的组合预测模型在金融产品价格预测方面的应用问题，以求有效监控市场上金融产品的价格变动，准确地进行金融产品价格变化趋势预测，以实现金融服务行业利润最大化的目标。

1 贝叶斯极大似然估计

设真值为yt，第i（i=1，…，m）种预测方法对t时刻真值的拟合值（t≤n）或预测值（t＞n）为yti。则真值与拟合值（或预测值）之间的关系可以由如下方程描述：

在式（1）中，uti为方程误差，E(uti)=0，αi，βi分别反映yti的“系统偏差”和尺度偏差。在这里，不妨将αi视为与所使用的预测方法相关联的误差。

由式（1）可得：

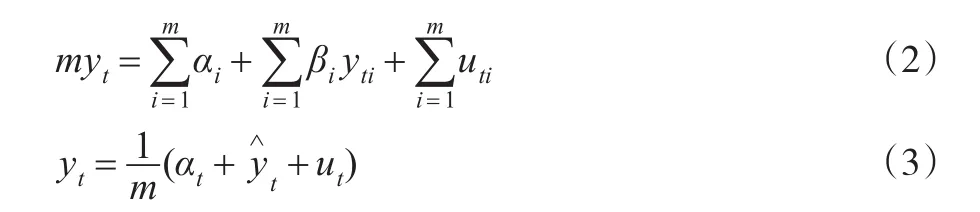
由式（3）可得，也服从下述分布：

求最大值：

也即求最小值：

从文献[6]可以得到αi、βi的极大二乘估计为：

式（6）所反映的权重为变权重。在本文中，将结合运用贝叶斯理论和IOWHA算子建立一种较好的变权重预测方法。

2 基于贝叶斯理论的IOWHA算子

以往的IOWHA算子在选择时，往往只是考虑当前时点的影响。事实上，需要综合考虑以往各期单项方法的预测精度来构建IOWHA算子。在本文中，将借鉴式（6）构建引导的算子。即设：

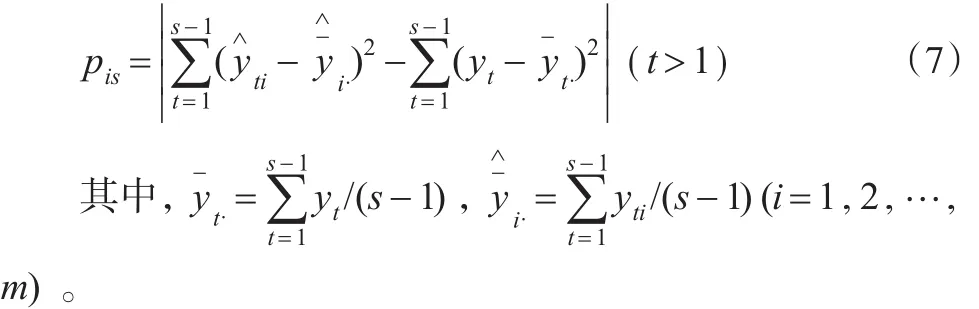
s指的是当期，m为方法的类别。也就是说，在这里充当算子的函数排除了当期数值的影响。如文献[5]所述，如果在对当期进行预测时，运用当期的数据，显得不太符合预测的含义，也不能得到真正意义上的组合预测值，以往很多论文对这一点的关注不够。

不过这里又带来了一个新的问题。即第一期的预测值怎么计算的问题。因为第一期没有预测的依据。因此，在本文中，破例在第一期，使用很多学者使用的方式，即用当期数据计算当期各方法所占权重。在这种情况下，可以将不利之处降到最低限度。

3 模型构建

令：

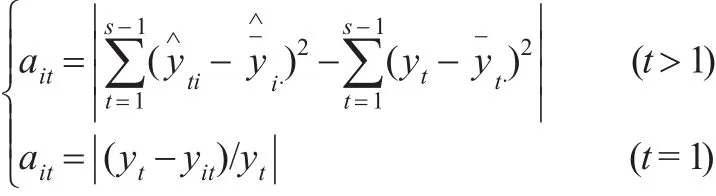
用ait表示第i种第t时刻的预测精度值。很显然，因为ait只起到引导排序的作用，因此，只要是非负值就可以了。

下一步，需要计算获得最优预测效果时的权重值。本文，将借鉴灰关联度的公式来构建。因此可以构建优化公式如下：

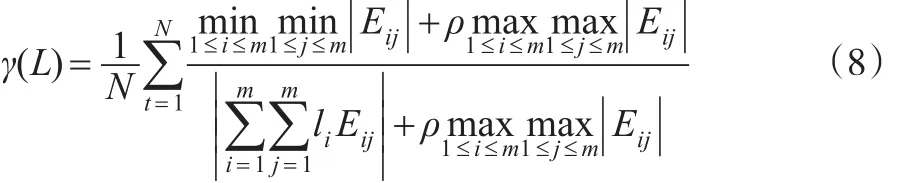
就误差值和误差矩阵而言，可以借鉴文献[8]中的设计方法，即：

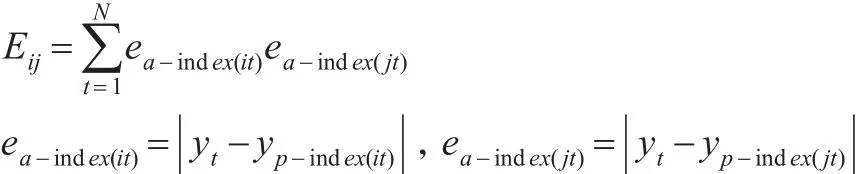
当γ越大则表示组合预测方法越有效可以被看作是常数（ρ一般取值0.5）。在这里，不妨令

则式（8）可以表示为：

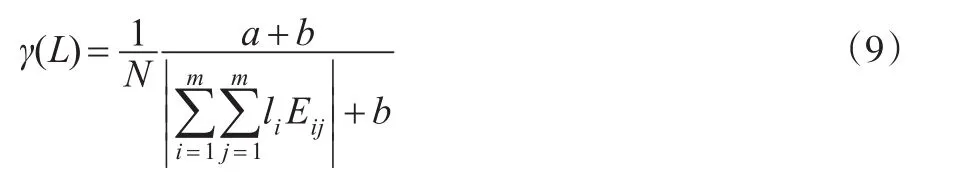
当式（9）取值最大时，则表明实际值与组合预测值的模拟效果最好。因此，可以建立组合预测模型如下：

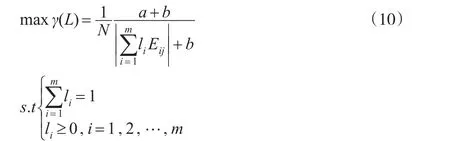
定理1：当优化公式为γ(L)关于L的偏导数存在，且进行泰勒级数展开时，可以得出权重向量L的最优解如下：

证明：

可构建如下所示的拉格朗日函数：

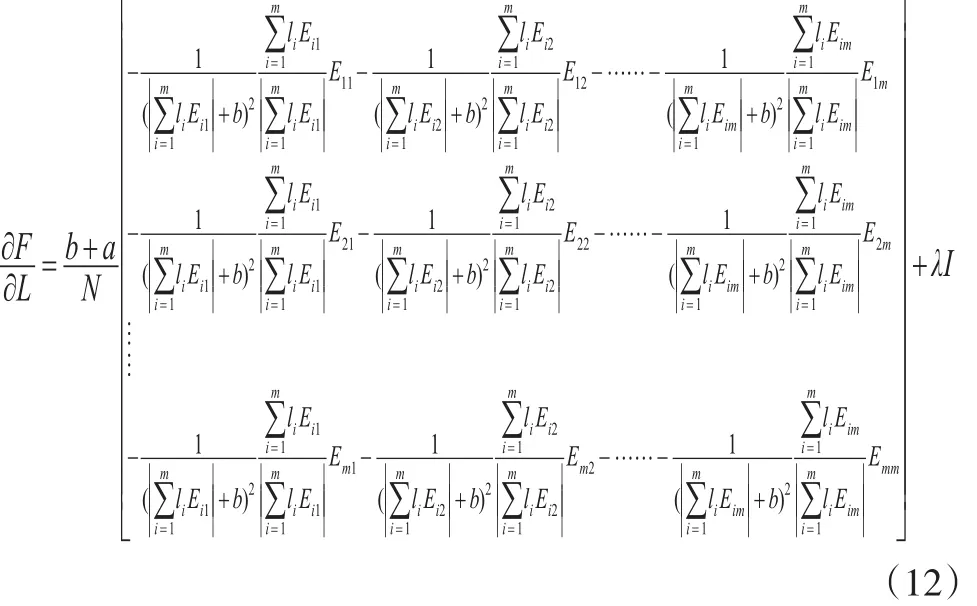
对L和λ分别取导数得：对式（12）可以使用泰勒级数在处进行一阶展

开。之所以这样设置，是因为在多期预测中，各单项方法所占权重趋向于一致。经过泰勒级数展开，式（12）可以转化为式（13）：

令：

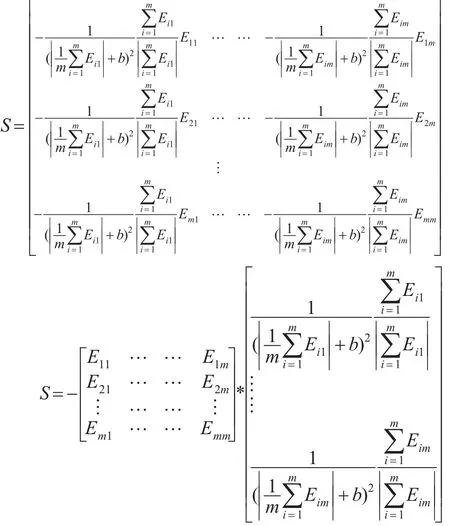
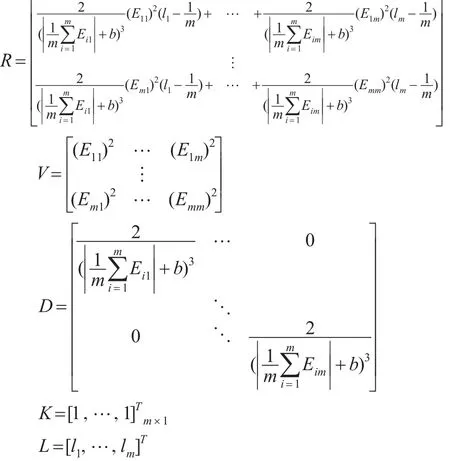
则式（13）可以表示为：

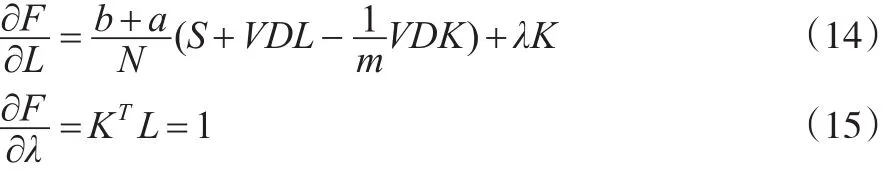
令式（14）和式（15）等于0，可以计算得出L的最优解如下：

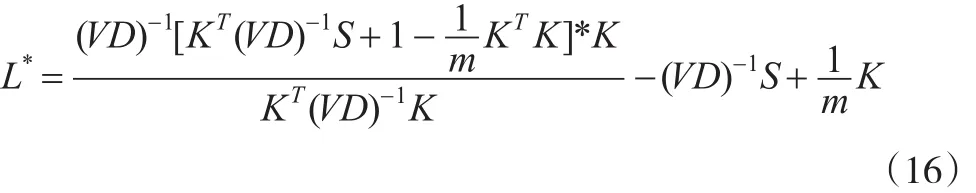
证毕。

4 算例分析

本文运用文献[8]中提出的五类指标来衡量基于贝叶斯最大似然的预测模型的有效性，这五类指标分别为：（1）平方和误差（2）均方误差（3）平均绝对误差平均绝对百分比误差（5）均方百分比误差

假定某种金融产品12个月的实际价格由参数yt表示，两个单项预测方法对金融产品价格的预测值由参数y1t、y2t表示，具体如表1所示。

表1 观测值与各单项预测方法预测值

运用本文所提供的预测方法，可以得到表1中两种单项方法的最优权重分别为：l1=0.5457，l2=0.4543。将上述权重值带入模型，可以计算出如表2所示的评价指标值。

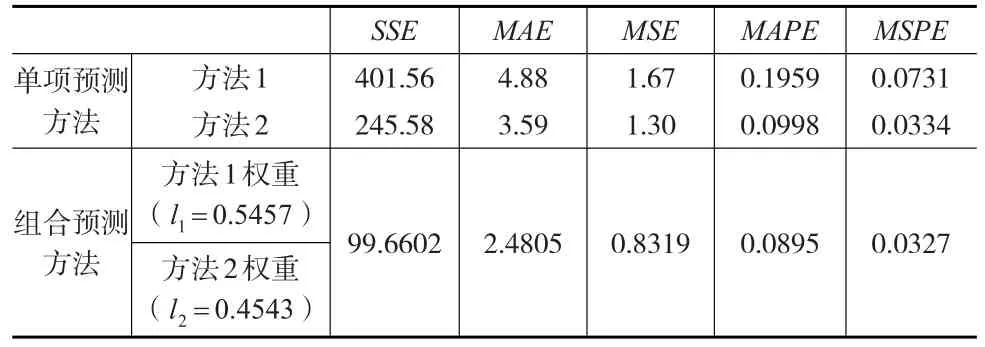
表2单项预测方法评价指标值与本文中的组合预测方法评价指标值对比表

从表2可以看出，本文给出的组合预测方法的预测效果较好。不过，因为在计算预测引导算子的表达式中，强调了以往各期预测值对于本期金融预测引导算子的重要性。当样本较少时，以往各期预测值的变动规律体现得不太明显，当样本越多时，规律体现得就越明显，而本文的引导算子就会越有效。

5 结束语

（1）在本文中，运用贝叶斯最大似然估计理论和表达式构建引导算子，从而，可以最大程度地反映以往各期金融产品价格预测值的变动规律。

（2）在本文中，运用灰关联理论构建最优权重值的确定模型，拓宽了权重值计算的思路，而值近似地体现了误差矩阵E中的某一个值，事实上也符合灰关联理论的相关规定性。（3）运用泰勒级数展开的方式对进行近似变换，为解决F关于L偏导数的求导问题提供了一个新的思路。

参考文献：

[1]鲍漪澜.基于支持向量机的金融时间序列分析预测算法研究[D].大连：大连海事大学硕士学位论文,2013.

[2]辛治运,顾明.基于最小二乘支持向量机的复杂金融时间序列预测[J].清华大学学报：自然科学版,2008,(7).

[3]廖薇,冯小兵,曹伟莹,刘锦高.广义回归神经网络的金融预测模型研究[J].商业时代,2010,(7).

[4]宋晓勇,陈年生.遗传算法和神经网络耦合的金融预测系统[J].上海交通大学学报,2016,(2).

[5]Yager R R.On Ordered Weighted Averaging Aggregation Operators in Multieriteria Decision Making[J].IEEE Transactions on Systems，Man，and Cybernetics，1988，18(1).

[6]Filev D，Yager R.R.On the Issue of Obtaining OWA 0perator Weights[J].Fuzzy Sets and Systems，1998，94(2).

[7]徐泽水，达庆利.一种组合加权几何平均算子及其应用[J].东南大学学报：自然科学版，2002，(32).

[8]陈华友，刘春林，盛昭瀚.IOWHA算子及其在组合预测中的应用[J].中国管理科学，2004,(5).

[9]张新育.组合预测的贝叶斯极大似然估计法[J].预测，1998,(5).

[10]张新育,杨松华,成立社,周世国.无尺度偏差和系统偏差组合预测的贝叶斯极大似然估计[J].预测，1999,(1).

[11]陆宜清,杨松华.多维组合预测的贝叶斯极大似然估计[J].郑州大学学报：工学版,2005,(3).