基于后悔理论的模糊多准则群决策方法
2018-04-26章恒全涂俊玮
章恒全,涂俊玮
(河海大学 商学院,南京 211100)
0 引言
近年来,模糊多准则群决策问题已成为国内外学者研究的热点。自Atanassov K T[1]基于模糊集理论[2]提出直觉模糊集(IFSs)以来,其理论发展也非常迅速,其拓展形式有以下4种:区间直觉模糊集(IVIFSs)[3]、三角直觉模糊集(TIFN)[4]、直觉梯形模糊集(ITFN)及区间直觉梯形模糊集(IITFN)[5,6]。IITFN的隶属度和非隶属度函数用区间数表示,在描述客观世界的不确定性本质上比IVIFSs,ITFN和TIFN更细腻和精确。
关于IITFN决策问题的研究有两种研究思路。一是通过不同的算子集结再根据排序方法进行选择[7-9];另一个是通过距离测度公式结合不同决策方法进行决策[10-12]。上述文献都可以较好地解决IITFN的多准则决策问题,但是都没有考虑决策者的心理行为对决策的影响。前景理论考虑了行为人风险偏好及损失规避等心理因素,并已经广泛的应用于多属性决策中。但前景理论需要参照信息,计算公式中需要确定众多的参数。而由Bell[13]和Loomes[14]提出的后悔理论,也是基于有限理性的假设考虑了决策者的心理特征的决策理论,已受到了专家学者的高度关注。由于后悔理论在决策应用中不需要给出参照点的信息,计算公式中只有一个后悔规避参数,因此,有学者指出后悔理论比前景理论更有优势[15,16]。本文针对准则值为IITFN的多准则群决策问题,在上述文献研究的基础上,将决策者的后悔规避心理行为引入决策中。由IITFN排序方法选择正理想方案和负理想方案,根据各方案与正理想方案的距离计算后悔函数值和各方案与负理想方案的距离计算其欣喜值,从而建立欣喜-后悔值矩阵;按决策者的偏好越大权重越小的思想确定决策权重,将各决策者的欣喜-后悔矩阵集结成群矩阵;构建非线性优化模型计算属性权重,由各方案的综合欣喜-后悔值对方案进行排序。并通过案例的选择实证检验了该方法的有效性和合理性。
1 基本理论
1.1 区间直觉梯形模糊数
定义 1[5,6]:设a͂=([a,b,c,d];ua͂,va͂)是实数集上的IIT-其区间隶属度函数为:
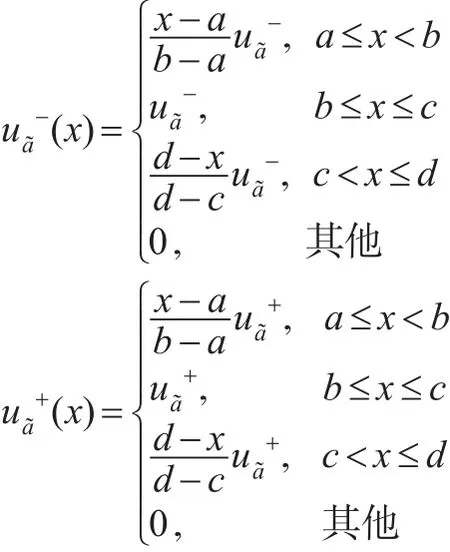
其区间值非隶属度函数为:

定义2[7,17]:设实数集上的IITFN是其分函数和精确函数的表达式分别是:
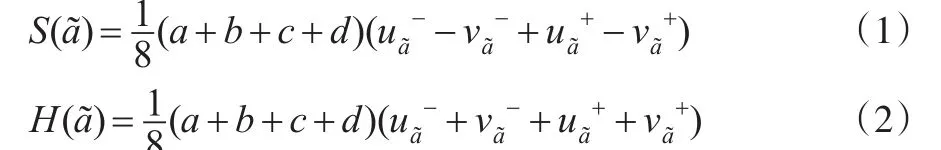
定义 3[7,16]:设为两个实数集上的 IITFN,其排序方法如下:
定 义 4[18]:设为 两 个 IITFN,则模糊数的距离为:

1.2 后悔理论
后悔理论[13,14]同时将后悔和欣喜两种心理感觉考虑到决策分析中,决策者具有后悔规避的的心理行为特点。各方案与其理想方案的比较能够得到欣喜-后悔值。以正理想方案的评价值为参考点,其他方案的评价值劣于正理想值,根据后悔理论可知决策者选择该方案是后悔的;而以负理想方案的评价值作为参考点时,则方案评价值大于负理想值,而决策者选择该方案是欣喜的。根据文献[14]第k个决策者对方案Ai的评价值Xij相对于负理想方案的欣喜函数和相对于正理想方案的后悔函数的表达式分别如下:

决策者对各方案评价值总的欣喜-后悔函数表达式如下:

2 基于后悔理论的模糊多准则群决策步骤
设某模糊多准则群决策问题,有m个备选方案,用Ai(i=1,2,…,m)表示,各评估准则为Cj(j=1,2,…,n),相应的准则权重向量为且wj∈[0,1]。决策群体为相应的决策权重为(w1,w2,且wk∈[0,1],其中决策者Ek关于准则Cj针对备选方案Ai的评价值为从而得到决策者Ek的区间直觉梯形模糊数的矩阵
步骤1:规范化处理决策矩阵
对模糊决策矩阵进行规范化处理,以消除各个准则由于量纲的差异对评价结果的影响。经转化的规范化模糊决 策 矩 阵 为
对于效益型准则,有[12]:
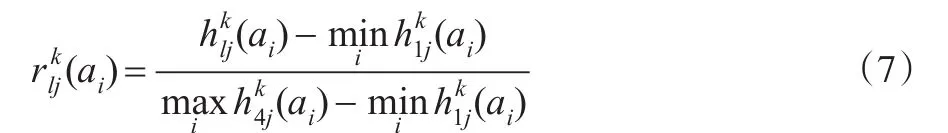
对?于成本性准则,有:
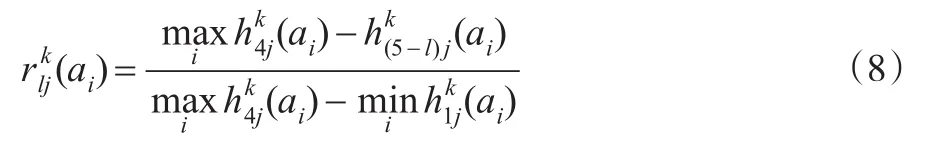
步骤2:确定决策者权重
首先根据区间直觉梯形模糊数的排序方法选择正负理想点,分别记为并计算出各方案到正负理想方案的距离。
针对决策权重信息未知的问题,根据决策者对最佳方案的偏好越大,决策权重越小的原理进行权重分配。决策者对正理想方案的评价越好,对负理想方案的评价越差,则偏好程度越大,因此决策者的偏好由最佳正理想方案和最佳负理想方案的距离来度量,具体计算如下:
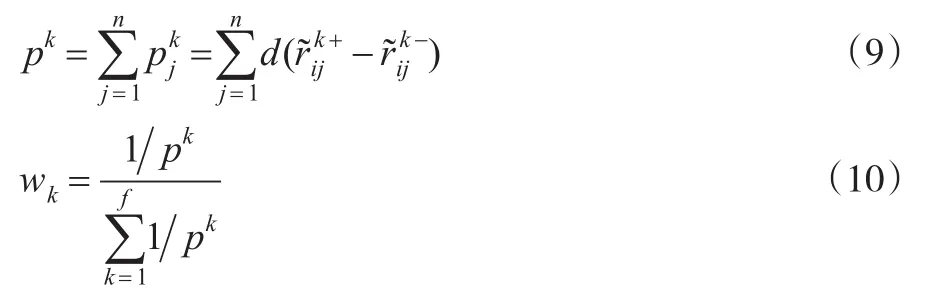
步骤3:确定各评价方案的欣喜-后悔函数
后悔理论中,欣喜值和后悔值都是各方案的评价信息相对于正、负参照点计算出的。可由距离公式(3)可以求出各方案到正负理想方案的距离,即与再求各决策者对方案Ai在准则Cj下的欣喜后悔函数为:

在按照式(6)求出欣喜-后悔值,根据WAA算子对不同决策者的欣喜-后悔值进行集结,方案Ai在准则Cj下的群体欣喜-后悔值为:

步骤4:确定属性权重,选择最优方案
近年来,利用极大熵原理求属性权重得到了广泛的应用,当权重熵值达到最大时,准则权重系列的不确定性最小。同时考虑方案Ai的评价值与正理想点的接近性,方案与正理想点距离越远,后悔值就越小(后悔值为负数);方案与负理想点距离越远,欣喜值就越大,而要调整权重系数 (w1,w2,…,wn)使欣喜-后悔值最大,因此,可以构建如下的目标优化模型:

将上述多目标问题转化为单目标问题,即:

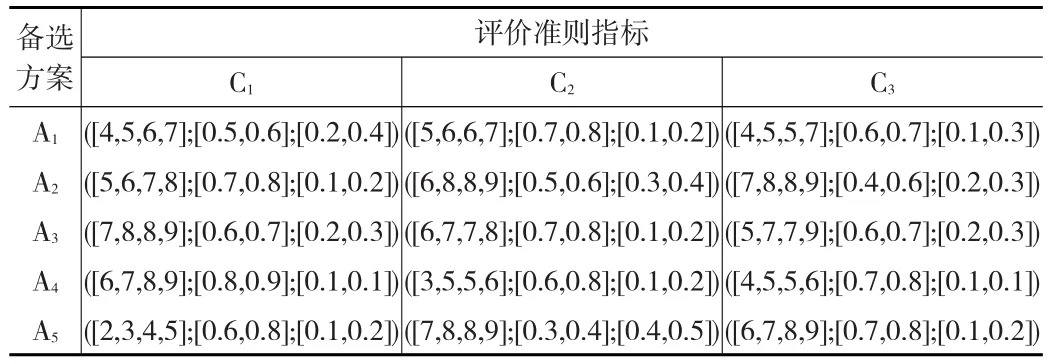
表1 专家E1给出的决策矩阵

表2 专家E2给出的决策矩阵

表3 专家E3给出的决策矩阵
其中0<λ<1,当两个优化目标函数进行公平竞争时,λ一般取0.5。运用运筹优化软件,可以方便的获取最优的准则权重,最后由准备权重计算出方案的综合欣喜-后悔值,根据欣喜-后悔值的排序选择出最优的方案。
3 算例分析
为验证该基于模糊多准则群决策方法的可行性和合理性,采用文献[11]中的算例,决策背景是:某城市计划在郊区建设一个冷库以储存多种生鲜产品,满足人们日益增加的对生鲜产品的需求。建设生鲜冷库的最核心的部分就是安装能够达到运行目标的空调系统,而安装空调系统必须考虑到冷库的空间结构等因素。项目承包人根据生鲜冷库的各项实际特征,在充分了解通风管道和水管布置情况、防火阀与消声器的布置状况等具体信息的基础上,给出了5种安装空调系统方案,简记为Ai(i=1,2,…,5)。组建专家小组(由不同领域的专家组成)对各方案进行评价,对安装空调系统的方案的主要评价一级准则有:经济性(C1)、功能性(C2)、操作性(C3),为了简化问题,并未考虑二级细分准则。假设共有3个专家Ek(k=1,2,3)对方案进行评价,并确定最终选择的方案。选择不同空调系统给生鲜冷库带来的效益不确定性存在风险态度的差异,因此考虑其决策行为基于有限理性的假设。同时,考虑到专家在对不同方案的评估认定过程中,由于熟悉程度的差异等因素导致认知的模糊性较强。所采用的模糊数应蕴含各专家提供的准则评价信息,区间直觉模糊数能够充分地反映出决策个体因个人偏好及信息相对不确定性等因素影响下产生的评估差异。最终,各决策者采用区间直觉梯形模糊数给出各个方案各准则的评估信息,评价信息如表1、表2、表3所示。
根据本文提出的针对评价信息为区间直觉梯形模糊数的多准则群决策方法,对空调系统选择的问题进行决策,具体步骤如下:
步骤1:三个评价准则中,经济性(C1)属于成本性准则,而功能性(C2)、操作性(C3)属于效益性准则。由式(7)、式(8)对3位专家给出的决策矩阵分别进行规范化处理,从而得出如下的规范化的决策矩阵:

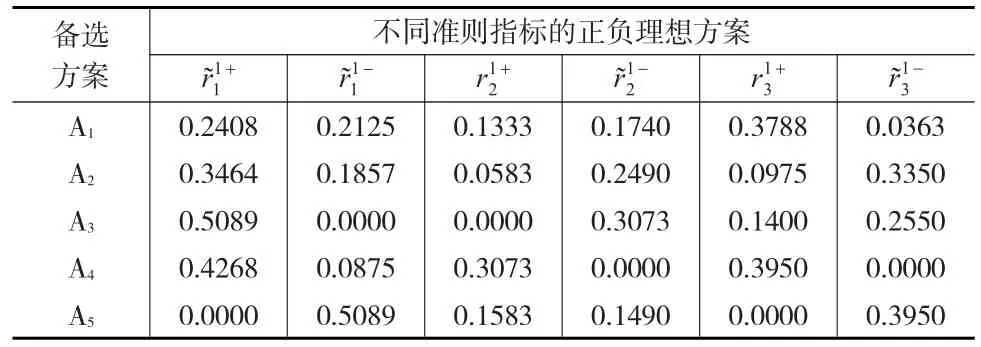
表4 E1的备选方案与其正负理想方案间的距离
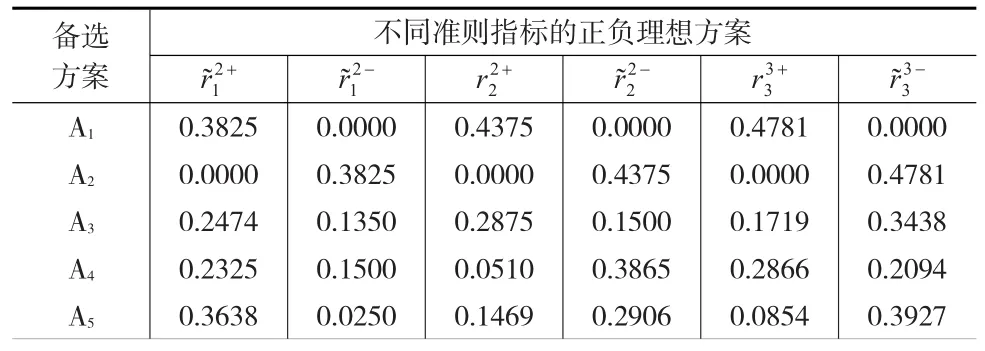
表5 E2的备选方案与其正负理想方案间的距离

表6 E3的备选方案与其正负理想方案间的距离
根据式(9)和式(10)求得wk分别为:0.3221、0.3006、0.3773。
步骤3:根据式(11)、式(12)、式(6)可求得各方案的欣喜-后悔值,由步骤2求出的决策者权重系数,把各决策者对各方案的欣喜-后悔矩阵集结成群决策的欣喜-后悔矩阵,如表7所示。
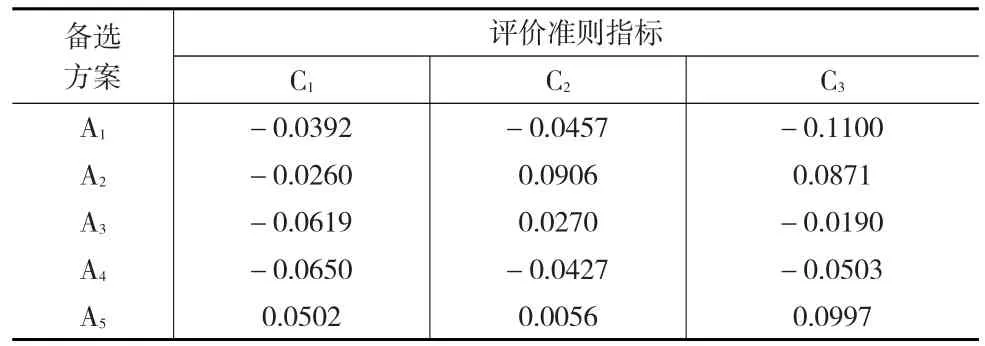
表7 群体决策的欣喜-后悔矩阵
步骤4:计算方案的指标权重

通过Lingo计算得到,各准则的权重系数分别是0.2981、0.3557、0.3462,最后计算各方案的欣喜-后悔值分别为 -0.0660、0.0546、-0.0154、-0.0520、0.0515。综合分析,欣喜-后悔值越大,则方案越优,可以得到各方案的排序:
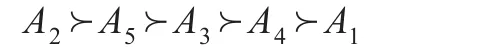
因此,方案A2是最优的决策方案,与文献[12]中的最优决策方案相同,说明改决策方法的有效性。但是两者的备选方案排序结果并不完全一致,文献[11]是运用各方案到正理想方案的灰色关联投影值比较的方法进行决策,属性权重是考虑决策矩阵到负极端矩阵与平均决策矩阵的距离计算,而本文属性权重是由各决策者的决策偏好大小决定,并考虑了心理行为影响因素,综合了各方案到正理想方案的后悔值与到负理想方案的欣喜值进行评优排序。
4 结束语
本文基于后悔理论,在限理性的假设基础之上,将决策者“后悔规避”的心理行为引入多准则群决策问题。针对采用区间直觉梯形模糊数表示特征值的决策问题,本文依据区间直觉梯形模糊数去模糊化来比较各方案准则评价值大小,确定正负理想方案作为各方案参考点,根据决策偏好大小计算决策者的权重,由此得出群决策的欣喜-后悔矩阵,基于极大熵思想和欣喜-后悔值最大原则确定最优准则权重,最后计算出各方案的综合欣喜-后悔值,对备选方案择优排序。该模糊决策方案综合考虑了准则的客观权重及决策者的心理因素,更加符合决策者的心理行为,且方法简单易于在计算机上操作。
参考文献:
[1]Atanassov K T.Lntuitionistic Fuzzy Sets[J].Fuzzy Sets and Systems,1986,20(1).
[2]Zadeh L A.Fuzzy Sets[J].Information and Control,1965,8(3).
[3]Atanassov K T.Interval Valued Intuitionistic Fuzzy Sets[J].Fuzzy Sets and Systems,1989,31(3).
[4]Shu M H,Chcng C H,Chang Jingrong.Using Intuitionistic Fuzzy Sets for Fault-Tree Analysis on Printed Circuit Board Assembly[J].Mi⁃croelectronics Reliability,2006,46(12).
[5]王坚强,张忠.基于直觉模糊数的信息不完全的多准则规划方法[J].控制与决策,2008,23(10).
[6]王坚强.模糊多准则决策方法研究综述[J].控制与决策,2008,23(6).
[7]万树平.基于区间直觉梯形模糊数的多属性决策方法[J].控制与决策,2011,26(6).
[8]周晓辉,姚俭,吴天魁.区间直觉梯形模糊Bonferroni平均算子及在多属性群决策中的应用[J].运筹与管理,2016,25(3).
[9]周晓辉,姚俭.基于Choquet积分的区间直觉梯形模糊多属性群决策[J].系统科学与数学,2015,(2).
[10]万树平.基于分式规划的区间梯形直觉模糊数多属性决策方法[J].控制与决策,2012,27(3).
[11]王海元,韩二东.灰色关联投影下的模糊多属性群决策方法[J].计算机工程与应用,2016,(19).
[12]付沙,唐晓波,刘钟理等.区间直觉梯形模糊数MADM问题的灰色关联分析方法[J].科技管理研究,2015,(5).
[13]Bell D E.Regret in Decision Making Under Uncertainty[J].Opera⁃tions Research,1982,30(5).
[14]Loomes G,Sugden R.Regret Theory:An Alternative Theory of Rational Choice Under Uncertainty[J].Journal of Economic,1982,92(368).
[15]Chorus C G.Regret Theory-Based Route Choices and Traffic Equi⁃libria[J].Transportmetrica,2012,8(4).
[16]Laciana C E.Weber E U.Correcting Expected Utility for Compari⁃sons Between Alternative Outcomes:A Unified Parameterization of Regret and Disappointment[J].Journal of Risk and Uncertainty,2008,36(1).
[17]Xu Z S.Intuitionistic Fuzzy Aggregation Operators[J].IEEE Transac⁃tions on Fuzzy Systems,2007,15(6).
[18]陈振颂,李延来.基于IITFN输入的复杂系统关联MAGDM方法[J].自动化学报,2014,(7).
