慢行交通混合过街特性及冲突模型研究
2018-04-25郭财贵
郑 柯 郭财贵
(福州大学 土木工程学院,福州 350108)
引言
近年来,中国各地政府纷纷倡导绿色出行,加强非机动车的发展。由于电动自行车廉价快捷、无需证照等特点,我国城市居民使用电动自行车的比例非常高。本文中研究的电动自行车为行驶在非机动车道与人行横道上的电动自行车,包括普通电动自行车和轻摩化的电动自行车。本文所研究的过街形式为:电动自行车与行人通过人行横道混合过街。在交叉口中,人行横道上的行人与电动自行车共同过街时会有许多的轻微交通冲突,这部分过街慢行交通的内部冲突会对行人与电动自行车混合过街产生较大干扰。
由于国外道路以机动车交通为主,对慢行交通安全研究较少。Fruin J定义行人冲突为:
由于过于靠近其他一个或多个行人,使得行人正常行走的速率受到中断或者暂停[1]。美国通行能力手册(2010)定义非机动车交通事件数为单位时间和单位道路长度内道路使用者之间相互逼近从而改变行驶状态的次数[2]。我国学者很早就开始对慢行交通安全进行研究。单晓峰把骑行者需要花额外精力做出的骑行行为,如减速、超车或者避让等定义为自行车事件数,通过事件数来描述自行车骑行者的舒适程度,并建立了路段上自行车事件数模型[3];周晨静等对信号交叉口自行车群释放速度特性进行了研究,获得了自行车群在绿灯时间里的释放速度规律[4];陈峻对南京多条行人-自行车共享道路路段进行调查,以实测数据为基础建立了自行车的超越与相遇冲突模型,并进行了敏感性计算[5];邓建华对人非共板上的行人和自行车进行研究,建立了人非共板条件下的混合交通流元胞自动机模型,通过阻挡概率来描述行人与自行车的干扰程度,用于评价交通运行状况[6];叶晓飞等研究了电动自行车与自行车的交通差异,建立了自行车交通事件数模型,得到电动自行车与自行车的换算系数计算公式[7]。综上所述,国内外对慢行交通做了一定的研究,但是行人与电动自行车混合过街的冲突研究尚处于空白。
借鉴交通冲突的定义以及已有慢行交通冲突的研究,本文定义人行横道上慢行交通混合过街冲突为:在慢行交通混合过街时,当慢行交通个体相互逼近,威胁到交通参与者(行人、电动自行车骑行者)的安全或使交通参与者感到不适,行人或骑行者必须花额外的精力采取一些行为避免危险发生,如超越前方速度较慢的慢行交通个体或者躲避对向或同向行进的慢行交通个体,这种现象称为慢行交通混合过街冲突。
1 数据调查与统计分析
由于本文不考虑机动车对过街慢行交通的影响,因此本文的调查地点选取以行人和电动自行车共同过街的信号交叉口人行横道。调查地点应符合以下要求:1)人行横道的各类慢行交通量应该足够大,并能够满足不同比例的要求;2)便于调查;3)过街形式为一次过街。选择在晴朗无异常天气和正常的道路交通情况下,工作日时间(周一上午到周五下午),每个调查点调查时间为下午4点到8点,每个时段调查前半小时,调查时间共2h,调查5个交叉口,共计调查10h。慢行交通速度调查见表1,密度与冲突数调查见表2。

表1 慢行交通速度调查表
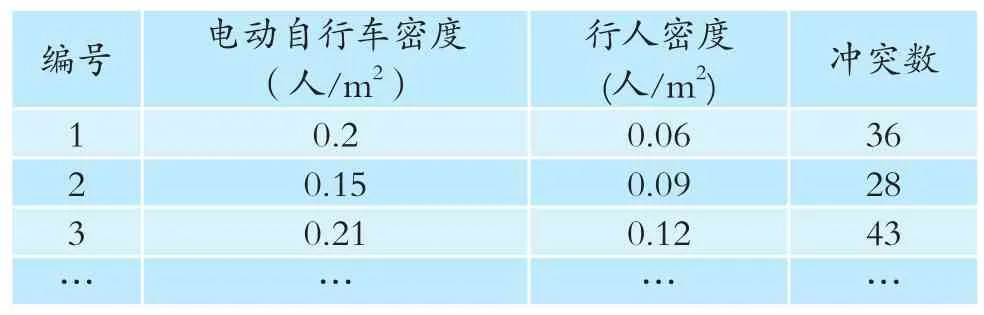
表2 密度与冲突数调查表
2 慢行交通混合过街特性分析
2.1 速度特性
在速度性能方面,电动自行车速度与加速度均大于行人,速度差异是造成人行横道慢行交通混合过街冲突的主要原因之一。本文使用行程速度来研究慢行交通混合过街速度特性。设慢行交通起始位置坐标为(X0,0),时刻为tik,通过人行横道的位置为(Xi,Y)(Y表示人行横道的长度),时刻为ti(k+1),则慢行交通通过人行横道的行程速度为:

对5个信号交叉口的慢行交通进行速度调查,使用SPSS软件对过街的混合慢行交通中各种交通方式的速度进行分析,研究在混合交通互相干扰下,各种交通方式的速度分布。调查共获得258个行人过街速度样本和245个电动自行车过街速度样本。电动自行车通过人行横道的平均速度频率分布如图1所示。电动自行车过街平均速度的均值是7.89km/h,标准差为2.00,从数值可以看出电动自行车过街速度较慢,虽然存在车群过街现象,但是由于受车辆性能、对向交通和驾驶行为的影响,过街速度有一定离散性。对速度样本进行K-S检验得到p值为0.204,大于0.05,可以认为电动自行车过街平均速度服从正态分布。根据贾海亮[8]对成都市7个交叉口进行调查,获得218个电动自行车通过非机动车行驶区的速度样本,统计得到人行横道长度小于7m时,电动自行车的速度为8.67km/h,而当距离为20m时,电动自行车的平均速度为17.42km/h。通过速度对比可得:当电动自行车与行人共同过街并且存在对向交通时,电动自行车的骑行受到了较大的干扰,骑行速度较慢。
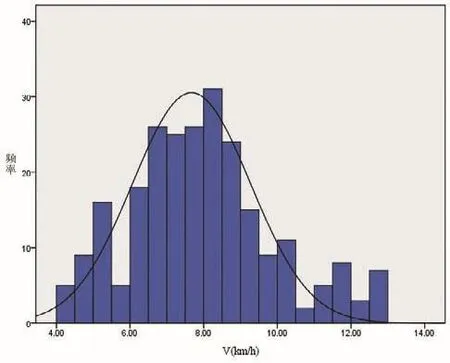
图1 电动自行车过街平均速度频率正态分布图
对行人过街平均速度进行统计分析,行人过街平均速度频率分布如图2所示。根据计算得到,行人过街平均速度为4.37km/h,标准差为0.66。对行人过街速度进行K-S检验得到行人过街平均速度显著性水平为0.673,大于0.05,因此,可以认为行人过街速度符合正态分布。冯树民[9]调查得出的哈尔滨人行横道行人速度为5.29km/h,陈然[10]实测上海市行人步行平均速度为4.46km/h,两项研究均大于本文调查统计得出的混合交通过街的行人平均速度,说明慢行交通混合过街对行人过街造成了一定的干扰,而且,与电动自行车相比,行人受到的影响较小。
图2 行人过街平均速度正态分布图
2.2 密度特性
本章研究各个不同交叉口的交通密度情况,定义慢行交通密度为某一时刻人行横道内单位面积内的当量慢行交通实体数。

调取五四路-湖东路交叉口高峰小时东西方向的人行横道视频数据,以2s作为时间间隔进行截图,调查每张截图人行横道中的慢行交通密度并记录,共调查10组高峰小时的绿灯放行时段,绘制慢行交通混合过街密度变化曲线图,如图3所示。
根据图3我们可以知道,慢行交通混合过街第一阶段慢行交通实体数迅速增加,时间较短暂;第二阶段人行横道中的慢行交通实体数达到饱和后呈现波动状态,随着进入人行横道的慢行交通个体减少而人行横道中的慢行交通个体不断离开人行横道,人行横道中的慢行交通实体数开始逐渐降低;当人行横道中交通实体数降到较低时,开始进入第三阶段,第三阶段对向相遇的慢行交通个体较少,人行横道中的慢行交通实体数继续减少。
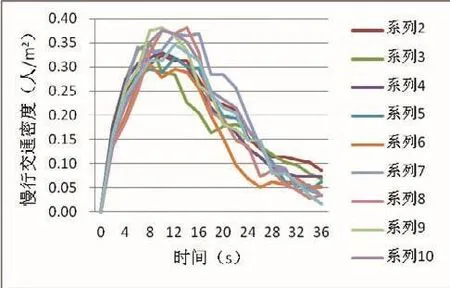
图3 慢行交通混合过街密度变化曲线
两个时刻的慢行交通密度差值与时间长度的比值为慢行交通实体数的变化斜率。取交通密度变化斜率平均值,可得慢行交通密度斜率表,如表3所示。
从表3中可以看出,交通密度在0-12s升高,12s之后开始下降,其中16-18s下降最快,达到了-5.2。结合现场的观测情况与图3,可以初步判断在交通密度下降速度达到最快之后,大量的慢行交通开始离开人行横道,慢行交通开始逐步从第二阶段进入第三阶段,根据行人步行速度与人行横道长度情况,此段时间在6-10s之间。

表3 慢行交通密度斜率表
2.3 速度与密度的关系
慢行交通中电动自行车和行人的比例并不是一个固定值,不同比例的慢行交通流参数不相同,因此引入一个慢行交通混合系数K:

本文调查了福州市5个十字交叉口的20个人行横道的不同时段慢行交通过街交通流,共获得108个符合要求的慢行交通速度和密度数据。对调查数据进行统计分析,分析K值在0.56-0.65之间的慢行交通流速度-密度关系,并参考K值为0的行人过街研究中的行人流速度和密度数据,绘制慢行交通速度-密度图,如图4所示。
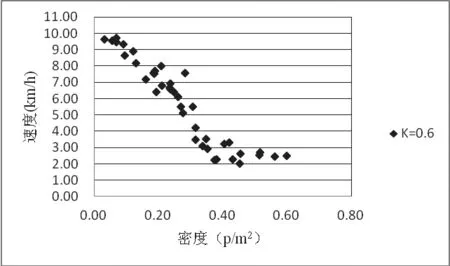
图4 慢行交通速度-密度分布图
分析图4可知:当密度较小时,慢行交通处于自由流状态,速度较高,混合的慢行交通平均速度在9km/h到10km/h之间;密度较大时,混合交通的速度大小分布在2km/h到3km/h之间。随着密度的提高,混合的慢行交通速度呈现下降的趋势。
3 慢行交通混合过街冲突模型
3.1 电动自行车与行人换算系数研究
本文研究的人行横道上的过街交通流是由行人和电动自行车组成的混合交通流,行人和电动自行车的动力性能和尺寸不相同,过街时占用的空间资源不同,而且两者的速度不同,相互间的影响也不相同。在研究慢行交通混合过街冲突时行人和电动自行车的交通量和交通密度是没有可比性的,需要将混合交通量换算成同一类型的交通量进行计算。因此,本文需要对电动自行车与行人的换算系数进行研究。
目前,对于换算系数的求解计算存在不同的观点和角度,因此换算系数的求解方法较多,主要有容量计算法、速度-流量计算法、道路占有率法、车头时距计算法等多种方法。本文采用时空资源占有率的方法计算电动自行车密度与行人密度的换算系数。电动自行车相对于行人的换算系数模型为:

电动自行车移动时的占用面积为:

电动自行车移动时的有效长度为:
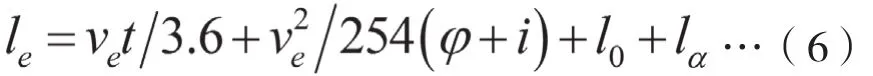
行人移动时的占用面积为:

以五四路口为例,电动自行车通过人行横道的平均时间为8.7s,行人通过人行横道的平均时间为15s。
根据以上研究,可以得到电动自行车相对于行人的换算系数为:

3.2 交通密度与冲突的关系模型
以交通冲突调查为基础,对本文研究的5个交叉口的20个人行横道进行交通密度调查,选取6min为时间间隔,记录每6min内慢行交通过街前两阶段内平均交通密度与交通冲突数,获得200组样本数。
使用电动自行车与行人换算系数,将交通方式统一换算成行人,使用SPSS软件对慢行交通密度ρ与冲突数TC进行回归分析,结果见表4。
通过表4可以发现,根据判定系数R2值,各回归模型的回归拟合程度都较高,其中R2值为0.841。
取二次方回归方程作为慢行交通冲突模型,二次方拟合回归如图5所示。得到拟合方程如下:
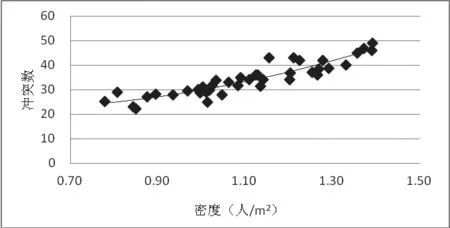
图5 二次回归方程图
交通密度与冲突数的回归方程与实际情况相符,当单位面积中的行人或电动自行车数量增多时,慢行交通密度增加,慢行交通个体之间的空间变少,容易产生摩擦和碰撞,因此慢行交通个体间的冲突数也会增加。
3.3 实例分析
取80组实测数据进行实例分析,根据交通密度与交通冲突回归模型可以预测交通冲突数,将冲突实测值与预测值作比较,得出图6。
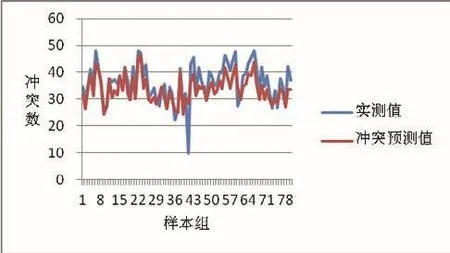
图6 冲突实测值与预测值比较

表4 慢行交通密度与冲突数回归分析结果
从图6可知,冲突回归模型预测的冲突值与冲突实测值曲线近似,说明本文建立的冲突回归模型能够较好地预测慢行交通混合过街的冲突情况。
4 结束语
(1)通过对5个交叉口的慢行交通速度调查,得到电动自行车过街平均速度的均值是7.89km/h,行人过街平均速度为4.37km/h,电动自行车和行人过街受到干扰,速度有所降低。
(2)慢行交通过街时,慢行交通密度先上升,后下降,分成三个阶段。
(3)慢行交通混合过街时,随着慢行交通密度的提高,慢行交通速度呈现下降的趋势。
(4)采用时空资源占有率的方法计算电动自行车密度与行人密度的换算系数,得到电动自行车与行人的换算系数为3.34。
(5)本文建立了交通密度与交通冲突的二元回归方程,并用实测数据验证了模型的有效性。
参考文献:
[ 1 ] Fruin J J. Pedestrian planning and design[R]. 1971.
[ 2 ] IBM中国商业价值研究院.未来的企业—中国企业的智慧转型[M].北京:东方出版社,2009.
[ 3 ] (美)戴布拉.艾米顿.创新高速公路:构筑知识创新与知识共享平台[M].北京:知识产权出版社,2005.
[ 4 ] (日)风田全启.专利.商标侵权攻防策略[M].北京:知识产权出版社,2005.
[ 5 ] (印)甘古力.知识产权:释放知识经济的能量[M].北京:知识产权出版社,2004.
[ 6 ] 刘振刚.企业知识产权管理理论与实务[M].北京:北京出版社出版集团,2007.
[ 7 ] (美)维坎.维奇克.城市公共交通运营、规划与经济[M].北京:中国铁道出版社,2012.
