Ar+轰击SrTiO3表面的持续光电导现象

何 鹏，幸代鹏，周 瑶，何 月，曾慧中

（电子科技大学 电子薄膜与集成器件国家重点实验室,四川 成都 611731）

近年来，研究发现Ar+轰击后的SrTiO3（STO）表面会表现出一些独特的光学、电学和磁学等奇异的物理性能。采用 Ar+轰击的方法在绝缘 SrTiO3单晶表面制备出具有准二维电子气特性的导电层[1-2]引起了学界的广泛关注。与通过在GaAs基上生长或LaAlO3/SrTiO3异质结获得二维电子气的外延技术相比，Ar+轰击技术具有操作简单、实验条件容易实现等优点，有利于器件的加工。随后，在 Ar+轰击的SrTiO3表面准二维导电层陆续发现了光致荧光[3]，磁阻效应[4]，持续光电导效应[5]，金属绝缘相变[6]，自旋轨道耦合[7-8]等物理现象，在存储、传感、场效应等纳米电子器件领域具有巨大的应用前景。其中，持续光电导效应可以用于光电存储器[9-11]，在全息存储领域有着十分重要的应用前景。

持续光电导现象早在20世纪80年代就被广泛地研究，这种物理现象主要在GaN[12]和GaInNAs[13]等半导体中出现。关于持续光电导的来源，一般理论认为 III-V族半导体中的持续光电导主要与深能级陷阱的大晶格弛豫（Large Lattice Relaxation）相关，而II-IV族混晶[14]中的持续光电导则是来源于组分涨落引起的随机局部势能涨落（Random Local Potential Fluctuations）。另外一些研究认为n-GaAs[15]掺杂层的持续光电导是来源于界面能带弯曲引起的宏观势垒（Macroscopic Barrier）。尽管有好几种不同的理论解释不同体系的持续光电导现象，但总的来说，持续光电导都与晶体内部缺陷的作用密切相关。

在 Ar+轰击的 SrTiO3表面，氧空位是主要的缺陷[3-4,16-17]。SrTiO3表面的持续光电导现象则认为与氧空位密切相关。比如，Tarun等[18-19]在真空退火的SrTiO3晶体上观察到了持续光电导现象，他们的研究表明持续光电导现象与退火形成的Ti—O空位对（VTi—O）和氧空位（VO）的大晶格弛豫有关。Kumar等[5]在 Ar+轰击的 SrTiO3表面也观察到了持续光电导现象，他们的研究结果认为SrTiO3的持续光电导只与氧空位的大晶格弛豫相关。目前，人们已经认识到氧空位在带间形成的深能级陷阱对SrTiO3持续光电导的主导作用。在已有的实验研究报道中，多采用紫外光源产生带间激发的方式研究持续光电流。这种方式既有本征激发，又有带间激发，而如果采用亚禁带（Sub-Band Gap）光激发方式，则只存在带间激发，光电导的产生和衰减对深能级陷阱将更加敏感，有望获得更多陷阱能级的信息[20-24]。为此，本文采用亚禁带光激发的方法研究Ar+轰击后SrTiO3表面导电层的持续光电导现象。由于采用的405 nm波长激光的光子能量（3.06 eV）小于SrTiO3的直接带隙[25]（3.75 eV）和间接带隙[26]（3.25 eV），因此基本可以激发整个禁带范围内的缺陷。

1 实验方法

SrTiO3的表面导电层采用Ar+轰击的方法形成。实验中，单面抛光的（110）晶向的SrTiO3尺寸是5 mm×5 mm×0.5 mm。为了便于电学测量，采用光刻技术在SrTiO3表面形成沟道面积为350 μm×150 μm的六电极的霍尔条图形。Ar+轰击采用霍尔源（JKY-LZY530A）在真空腔体中进行，本底真空为8.0×10–4Pa。轰击时，氩气压维持在0.05 Pa。霍尔离子源的加速电压为120 V，放电电流为0.8 A。轰击结束后，依次用丙酮和酒精去除表面的光刻胶，再利用金属掩模在电极区域上依次溅射沉积 30 nm和50 nm厚的钛、铂金属电极，形成欧姆接触，以用于电输运特性和光电导测量。

电输运特性采用变温霍尔测试系统，测试电流100 μA，磁场强度1 T。光电流测量在真空变温探针台内完成。样品温度由低温控制器（Lakeshore 336）控制，温度范围为80～300 K，温度波动小于0.05 K。激光辐照由405 nm半导体激光器通过光纤引入变温探针台，直接照射样品表面。光纤末端的激光输出功率采用激光功率探测器标定。在整个变温光电导测试过程中，样品保持在1.0×10–5Pa的真空中，避免了气体吸附的影响。光电导采用数字电压电流源表（Keithley 2636B）进行测量，电压0.5 V，电流随时间的变化由计算机自动采集，最小采样间隔保持在100 ms以内，激光照射样品时间为200 s，光电导衰减测试所采用的光照强度均为5×10–3W/cm2，衰减曲线测试时间大于1000 s。

2 实验结果

图 1（a）是 SrTiO3面电阻(Sheet Resistance)和温度的依赖关系。样品在整个测试温度区间（80～300 K）呈现出与金属相似的电阻温度关系，在所测试范围内，样品的面电阻可以由公式进行拟合：

式中：R0是剩余电阻；R1代表电子与电子的作用；R2代表电子与声子的散射；R3代表传导电子与局域电子的交换耦合作用。实线是拟合曲线，得到的拟合参数分别是 R0=2976 Ω，R1=0.05 Ω/K2，R2=1.3×10–10Ω/K5和 R3=715 Ω/lnK。在金属性的SrTiO3中，面电阻的主要贡献来源于电子与电子的相互作用。图1（b）是迁移率(Mobility)和载流子浓度(Carrier Density)与温度的依赖关系。在300 K时，迁移率为 6 cm2…V–1…s–1，随着温度降低至 80 K，迁移率增加到 142 cm2…V–1…s–1；而载流子浓度从2.5×1014cm–2增加到 2.9×1014cm–2，保持在 2×1014cm–2的量级。迁移率的大小以及载流子浓度与其他报道基本一致[5]。

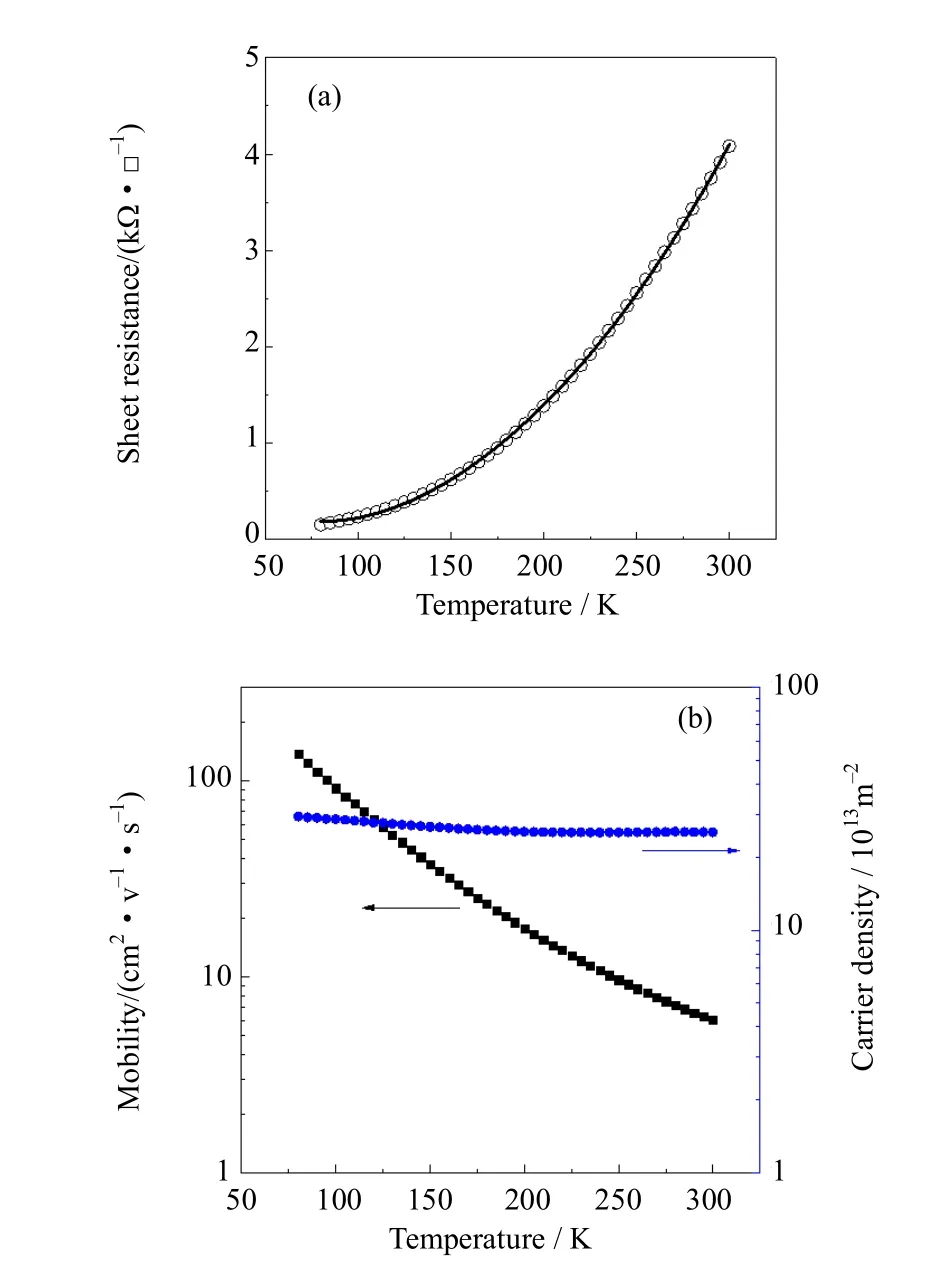
图1 (a) Ar+轰击SrTiO3的面电阻与温度依赖关系，实线是公式（1）在温度区间的拟合曲线；（b）迁移率和载流子浓度与温度的依赖关系Fig.1 (a) Temperature dependence of the sheet resistance in Ar+ bombardment SrTiO3, the solid line is best fit to the equation (1), within the temperature range of 80 K to 300 K; (b)Temperature dependence of mobility and sheet carrier density in the range of 80 K to 300 K

图2是SrTiO3表面光电导与激光功率的关系。光电导的定义为：

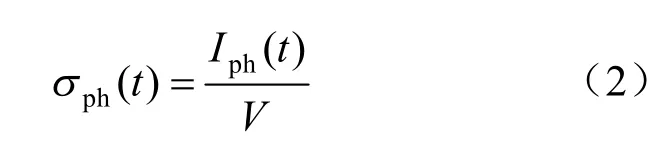
式中：V是两个探针之间的电压降；Iph(t)是照光之后的电流I(t)与照光之前的暗电流Id的差值。光电导的大小与激光从禁带中的缺陷激发到导带中的电子数量Δn相关。随着激光照射时间增加，光电导趋于饱和，电子数量Δn由电子激发速率和复合速率的稳定差值决定。激光的波长越短，其光子能量越高，可以将更接近价带下方陷阱中的电子激发到导带，光电导也就更大。图2（a）是300 K真空环境下用不同功率激光照射下的光电流-电压曲线，光电流随着光强的增加而增加，说明激光功率强度增大，激发到导带的电子数量随之增多，从而光电流也变大。

图2（b）是样品在温度80～300 K范围内饱和光电导与激光功率强度的关系。其实验数据满足幂律

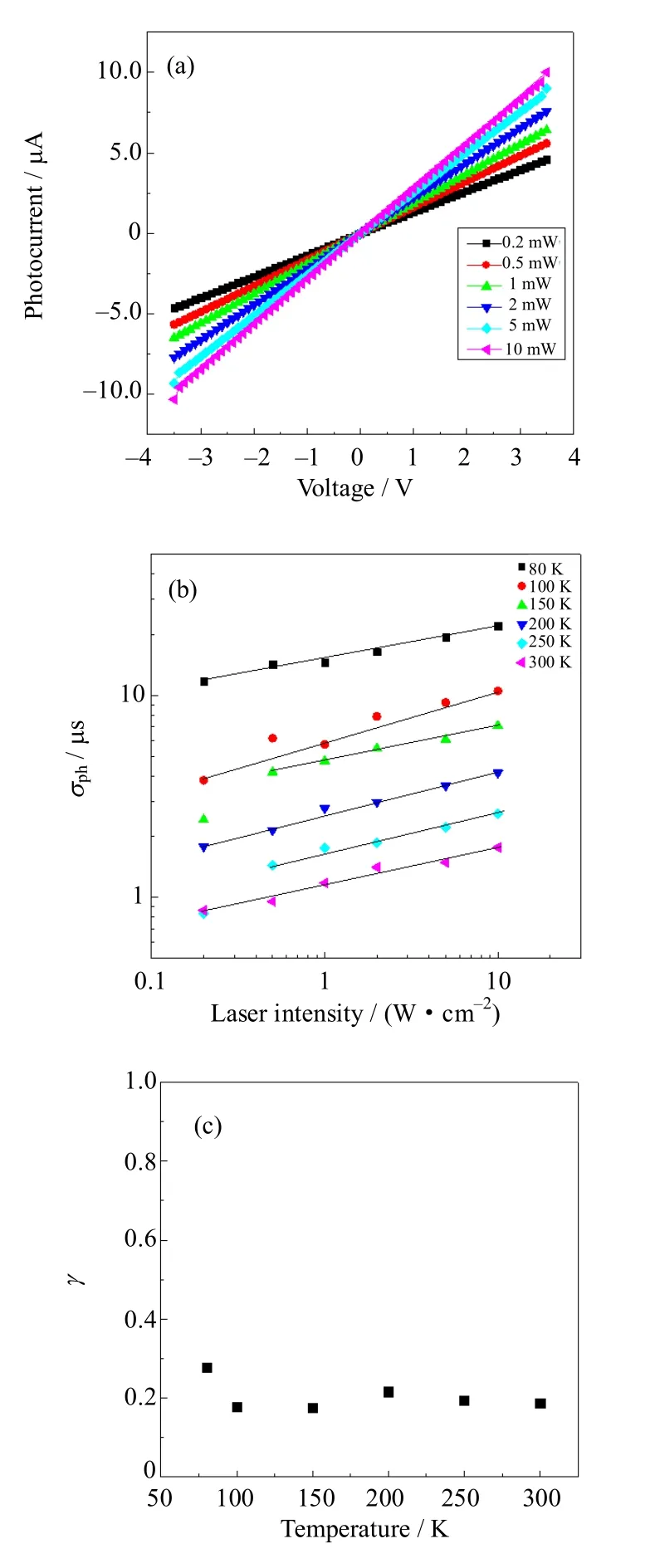
图2 （a）不同功率强度的的光电流-电压曲线；（b）不同温度下的SrTiO3饱和光电导与功率关系；（c）指数γ与温度的依赖关系Fig.2 (a) The photocurrent-voltage curves in STO under the irradiation at different light intensity; (b) Power intensity dependence of the saturated photoconductivity of STO at different temperature; (c) Temperature dependence of the exponent γ

表达式：

式中：P是激光功率；γ表示产生光生载流子时几个不同次能带的填充状态，γ值的大小取决于它的复合机制。图2（c）是指数γ与温度的依赖关系。本文的γ值在不同温度下基本上保持不变，大小都在0.2左右。在复合过程中，γ值有两个特殊值，当γ=1的时候表明是单分子复合过程，即分立能级的发光只与一种分子的数量相关，光电导的衰减符合指数规律；而γ=0.5时则表明是双分子复合过程，它的分立能级发光与两种分子的数目相关，光电导衰减形式是双曲线的。对于多数材料而言，γ值既不等于0.5也不等于 1，表明陷阱是连续分布的而不是孤立能级。图2（c）中的实验结果表明：SrTiO3的饱和光电导与功率的幂律关系表明了带间连续分布的陷阱能级是光电导的主要贡献。

图3（a）是不同温度下的光电导与时间的关系。可以发现饱和光电导随着温度的降低而增加，它的变化分为两个区域，当温度高于150 K的时候，饱和光电导增加缓慢，而当温度低于150 K的时候，饱和光电导增加迅速。图3（b）所示的是饱和光电导与温度倒数的关系。在温度80～300 K之间，饱和光电导与温度倒数的关系是两段直线，因此光电导与温度的关系可以通过阿伦尼乌斯公式来表示：

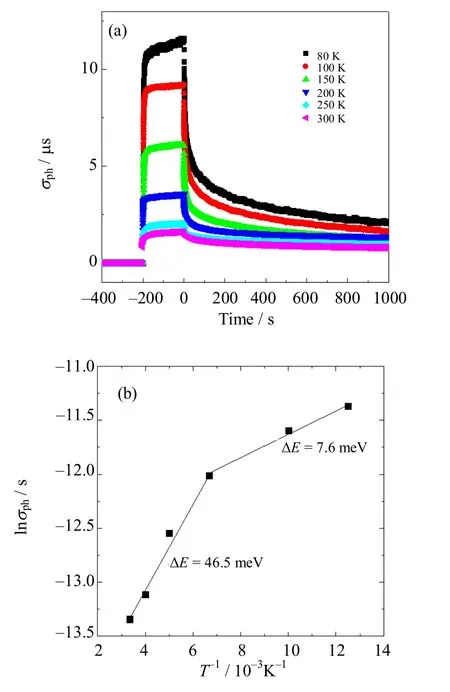
图3 （a）不同温度下的光电导与时间依赖关系；（b）饱和光电导与温度的关系。黑色直线是拟合曲线Fig.3 (a) Temporal dependence of the photoconductivity at various temperature; (b) Logarithm of the saturated photoconductivity as a function of reciprocal temperature. The black solid lines are the fitting curves

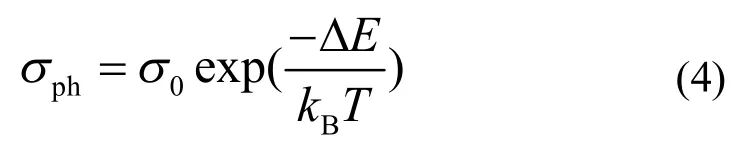
式中：σ0是与材料相关的指数因子；kB是玻尔兹曼常数；T是热力学温度；ΔE是光激活能。低温区域（80 ～150 K）的光激活能是7.6 meV，而室温附近（150 ～300 K）的光激活能是46.5 meV。这表明测试温度范围内有两个不同的光激活过程，在两个不同温度区间分别有不同能级位置的浅陷阱对饱和光电导有贡献。

低温区和室温区不同的光电导行为在光电导衰减实验结果中体现得更明显。图4所示的是光电导衰减与温度的关系。光照之后的SrTiO3表面的光电导衰减曲线可以由扩展指数型方程式进行拟合：

式中：β是弥散系数；τ是弛豫时间常数；t是时间。图4（a）所示的是不同温度下的光电导衰减曲线。图4（b）是不同温度下的归一化光电导衰减曲线，如图所示，温度越高，光电导衰减越慢。不同温度下衰减特征可以由弛豫时间常数 τ反映。不同温度下的光电导衰减曲线可以被公式（5）较好地拟合。在所有的测试温度下，β值随温度基本不变，保持在0.2左右，如图4（c）所示；弛豫时间常数τ是一个与温度相关的常数。弛豫时间常数随温度的变化同衰减特征一致，随温度的升高而增加。特征弛豫时间常数从80 K的49.6 s增加到300 K的2706 s。在polyparaphenylenevinylene[27]、LaAlO3/SrTiO3[28]、SrTiO3[29]、Cu2ZnSnS4[30-31]和 Zn0.3Cd0.7Se[32]等体系中也存在相似的弛豫时间与温度的关系。

3 讨论

解释持续光电导现象的模型主要有三种。一种是大晶格弛豫模型，该模型认为持续光电导现象主要来源于禁带中的深能级陷阱，不同缺陷之间强相互作用会产生一个势垒阻止电子空穴的复合。大晶格弛豫模型中，温度越高，电子具有的热能也更高，更容易越过势垒与空穴复合，所以，大晶格弛豫引起持续光电导的弛豫时间常数随温度的升高而减小。而本文持续光电导的弛豫时间常数随温度的升高而增大，不符合大晶格弛豫模型。宏观势垒模型是由于表面或者界面的能带弯曲使电子空穴对产生空间分离，从而使电子空穴的复合需要较长的时间，因此造成了持续光电导现象，它的光电导衰减形式一般是指数衰减，与本文的衰减形式不一致。随机局部势能涨落模型和宏观势垒模型类似，它认为持续光电导现象是由于组分涨落或者重掺杂引起的能带弯曲。符合随机局部势能涨落模型的持续光电导的弛豫时间常数随温度变化趋势与大晶格弛豫模型的弛豫时间常数变化相反，它的弛豫时间常数随着温度的升高而增加。本文持续光电导的弛豫时间常数随温度的升高而增大，与随机局部势能涨落模型的弛豫时间常数与温度的变化关系一致。对随机局部势能涨落模型而言，电子在低温区域随机分布在所有势阱之中，浅势阱中电子对复合起主导作用；而电子在高温区域主要位于深势阱之中，减小了电子空穴复合的概率，因此复合时间变长，持续光电导现象更加明显。

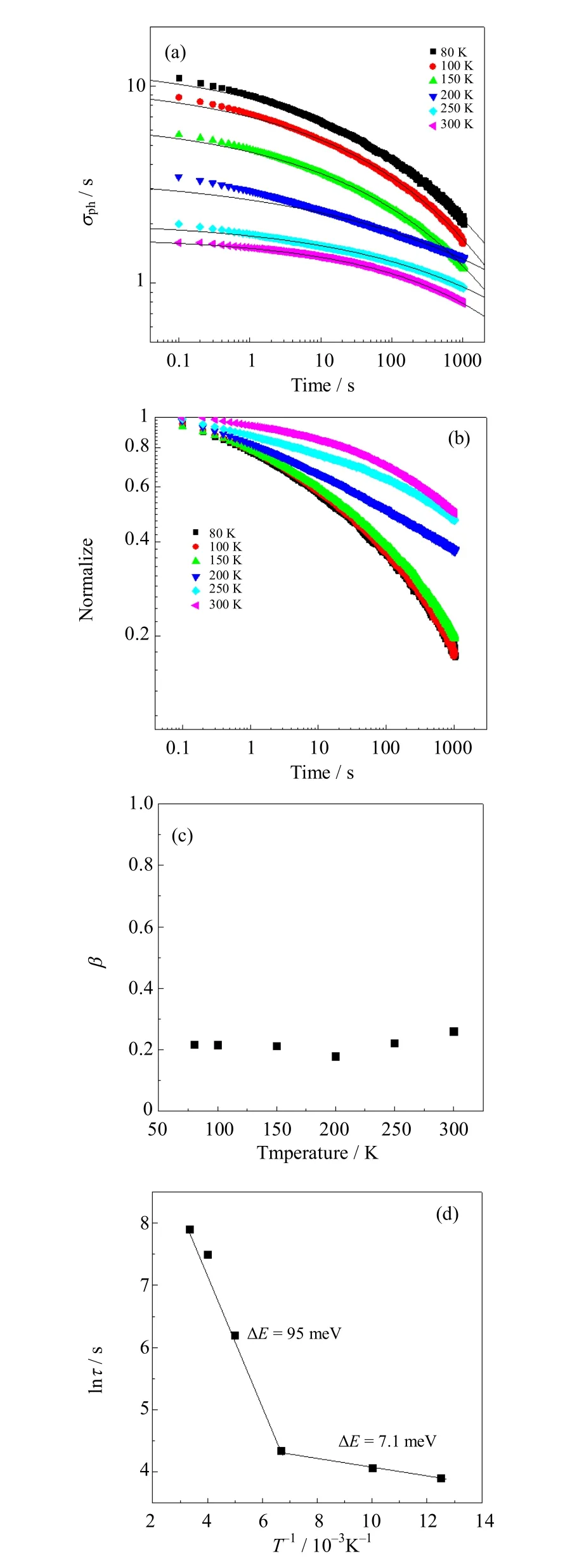
图4 （a）不同温度下的光电导与时间依赖关系。黑色曲线是用公式(4)拟合的曲线；（b）不同温度下的光电导归一化曲线；（c）弥散参数与温度的关系；（d）弛豫时间常数与温度倒数的关系。黑色直线是阿伦尼乌斯公式拟合曲线Fig.4 (a) Time dependence of the photoconductivity at different temperature. The solid lines are the fits to the equation(4); (b) Show the temporal dependence of the normalize photoconductivity at various temperature; (c) Temperature dependence of the dispersion parameters; (d) Logarithm of the relaxation time as a function of reciprocal temperature. The black solid lines are the fitting curves

本文的弛豫时间常数与温度的变化可分为两段，在低温区域（80～150 K）弛豫时间常数随温度的变化较小，而在室温附近（150～300 K）的弛豫时间常数随温度的变化较大。不同温度下的弛豫时间常数的变化与电子的热激活过程密切相关，两者的关系可用阿伦尼乌斯公式表示：

式中：τ0是指数因子；ΔE是克服势垒的热激活能；T是温度。如图4（d）所示，弛豫时间常数随着温度的升高而增加；在测试的温度区间里有两个不同的热激活过程，与图3（b）所示的饱和光电导与温度的关系类似。在低温区域，热激活能非常小，只有7.1 meV；而在室温附近区域，热激活能是比较大的，可以达到95 meV。因此，持续光电导在高低温区存在着两种不同的复合过程。

这种SrTiO3表面持续光电导衰减的弛豫时间常数随温度的变化趋势可以用带边的随机局部势能涨落模型来解释。导带的势阱深度是随机分布的，电子随机局域在导带的不同势阱之中。在低温的时候，浅势阱中的电子与空穴复合。此时，由于电子的势阱深度较浅，因此复合所需要的热激活能也比较小。当温度有所增加时，局域在浅势阱中的电子可以向深势阱漂移，更多的电子空穴对得以分离，进而使得持续光电导现象更加明显。温度继续增加，局部势能涨落减小，能带变得趋于平坦，电子从势阱中的跃迁势垒更大，更倾向于局域在深能级势阱之中，复合需要的时间也更长。因此，持续光电导现象变得更加明显。所以，可以认为SrTiO3表面光电导的衰减在低温时由浅能级陷阱的复合占主导，而在室温时则由深能级陷阱的复合占主导。

4 结论

本文报道了亚禁带光激发 Ar+轰击 SrTiO3表面的持续光电导效应。在温度80～300 K的范围内，饱和光电导与激光功率强度之间呈现幂律规律，表现出带间陷阱复合的特征。氩离子轰击 SrTiO3表面的持续光电导现象随温度的升高而增强，符合随机局部势能涨落模型，在低温时由浅能级陷阱的复合占主导，而在室温时则由深能级陷阱的复合占主导。

参考文献：

[1]SANTANDER-SYRO A F, COPIE O, KONDO T, et al.Two-dimensional electron gas with universal subbands at the surface of SrTiO3[J]. Nature, 2011, 469(7329):189-193.

[2]REAGOR D W, BUTKO V Y. Highly conductive nanolayers on strontium titanate produced by preferential ion-beam etching [J]. Nat Mater, 2005, 4(8): 593-596.

[3]KAN D S, TERASHIMA T, KANDA R, et al. Blue-light emission at room temperature from Ar+-irradiated SrTiO3[J]. Nat Mater, 2005, 4(11): 816-819.

[4]BRUNO F Y, TORNOS J, GUTIERREZ D O M, et al.Anisotropic magnetotransport in SrTiO3surface electron gases generated by Ar+irradiation [J]. Phys Rev B, 2011,83(24): 245120.

[5]KUMAR D, HOSSAIN Z, BUDHANI R C. Dynamics of photogenerated nonequilibrium electronic states in Ar+-ion-irradiated SrTiO3[J]. Phys Rev B, 2015, 91(20):205117.

[6]WANG Q R, ZHANG W L, ZHANG W X, et al. In-situ monitor of insulator to metal transition in SrTiO3by Ar+irradiation [J]. Appl Surf Sci, 2016, 365: 84-87.

[7]WANG Q R, ZHANG W L, PENG B. Universality and difference of electronic and spin transport properties at the irradiated oxide surface [J]. J Phys D: Appl Phys, 2017,50(37): 375302.

[8]ZHANG W X, WANG Q R, PENG B, et al. Spin galvanic effect at the conducting SrTiO3surfaces [J]. Appl Phys Lett,2016, 109(26): 262402.

[9]RASTOGI A, BUDHANI R C. Solar blind photoconductivity in three-terminal devices of LaAlO3/SrTiO3heterostructures [J]. Opt Lett, 2012, 37(3):317-319.

[10]TEBANO A, FABBRI E, PERGOLESI D, et al.Room-temperature giant persistent photoconductivity in SrTiO3/LaAlO3heterostructures [J]. ACS Nano, 2012, 6(2):1278-1283.

[11]LU H, LIAO Z, ZHANG L, et al. Reversible insulator-metal transition of LaAlO3/SrTiO3interface for nonvolatile memory [J]. Sci Rep, 2013, 3: 2870.

[12]HIRSCH M T, WOLK J A, WALUKIEWICZ W, et al.Persistent photoconductivity in n-type GaN [J]. Appl Phys Lett, 1997, 71(8): 1098-1100.

[13]LI J Z, LIN J Y, JIANG H X, et al. Persistent photoconductivity in Ga1–xInxNyAs1–y[J]. Appl Phys Lett,1999, 75(13): 1899-1901.

[14]JIANG H X, LIN J Y. Percolation transition of persistent photoconductivity in II-VI mixed crystals [J]. Phys Rev Lett, 1990, 64(21): 2547-2550.

[15]QUEISSER H J, THEODOROU D E. Hall-effect analysis of persistent photocurrents in n-GaAs layers[J]. Phys Rev Lett, 1979, 43(5): 401-404.

[16]KAN D, KANDA R, KANEMITSU Y, et al. Blue luminescence from electron-doped SrTiO3[J]. Appl Phys Lett, 2006, 88(19): 191916.

[17]SCHULTZ M, KLEIN L. Relaxation of transport properties in electron-doped SrTiO3[J]. Appl Phys Lett, 2007, 91(15):151104.

[18]TARUN M C, SELIM F A, MCCLUSKEY M D. Persistent photoconductivity in strontium titanate [J]. Phys Rev Lett,2013, 111(18): 187403.

[19]MCCLUSKEY M D, TARUN M C. Defects and persistent conductivity in SrTiO3[J]. AIP Conf Proc, 2014, 1583:319-322.

[20]VANMAEKELBERGH D, HAMSTRA M A, VAN PIETERSON L. Free carrier generation in semiconductors induced by absorption of sub-band gap light. A photoelectrochemical study with nanoporous GaP [J]. J Phys Chem B, 1998, 102(41): 7997-8004.

[21]OHTOMO M, SHIMADA T, HASEGAWA T. Correlation between gap states and off-current in pentacene field-effect transistors observed by sub-band-gap photocurrent-voltage measurement [J]. Jpn J Appl Phys, 2007, 46(34):L817-L819.

[22]BHATNAGAR A, KIM Y H, HESSE D, et al. Sub-band level-assisted photoconduction in epitaxial BiFeO3films [J].Appl Phys Lett, 2014, 105(12):122905.

[23]MOAZZAMI K, MURPHY T E, PHILLIPS J D, et al.Sub-bandgap photoconductivity in ZnO epilayers and extraction of trap density spectra [J]. Semicond Sci Technol,2006, 21(6): 717-723.

[24]MURPHY T E, MOAZZAMI K, PHILLIPS J D.Trap-related photoconductivity in ZnO epilayers [J]. J Electron Mater, 2006, 35(4): 543-549.

[25]VAN BENTHEM K, ELSASSER C, FRENCH R H. Bulk electronic structure of SrTiO3: experiment and theory [J]. J Appl Phys, 2001, 90(12): 6156-6164.

[26]ZHANG H, YAN L, HABERMEIER H. Unusual ultraviolet photoconductivity in single crystalline SrTiO3[J].J Phys Condens Matter, 2013, 25(3): 035802.

[27]DULIEU B, WERY J, LEFRANT S, et al. Intrinsic and extrinsic photocarriers in polyparaphenylenevinylene [J].Phys Rev B, 1998, 57(15): 9118-9127.

[28]JIN K X, LIN W, LUO B C, et al. Photoinduced modulation and relaxation characteristics in LaAlO3/SrTiO3heterointerface [J]. Sci Rep, 2015, 5: 8778.

[29]JIN K X, LUO B C, LI Y F, et al. Photoinduced phase transition and relaxation in bare SrTiO3single crystals [J]. J Appl Phys, 2013, 114(3): 033509.

[30]GONZÁLEZ J C, RIBEIRO G M, VIANA E R, et al.Hopping conduction and persistent photoconductivity in Cu2ZnSnS4thin films [J]. J Phys D: Appl Phys, 2013,46(15): 155107.

[31]ABELENDA A, SÁNCHEZ M, RIBEIRO G M, et al.Anomalous persistent photoconductivity in Cu2ZnSnS4thin films and solar cells [J]. Sol Energy Mater Sol Cells, 2015,137: 164-168.

[32]JIANG H X, LIN J Y. Persistent photoconductivity and related critical phenomena in Zn0.3Cd0.7Se [J]. Phys Rev B,1989, 40(14): 10025-10028.