高温线管式静电除尘器内颗粒捕集的解析方法

王锡辉， 陈厚涛， 杨 光， 肖 刚

(1. 国家电网湖南省电力公司电力科学研究院， 长沙 410007；2. 浙江大学 能源清洁利用国家重点实验室， 杭州 310027)

符号说明：

r——以阴极线为圆心的半径，m

ρa——所有粒径颗粒质量浓度，kg/m3

R0——阳极管半径，m

Fb——浮力，N

r2——以阴极线为圆心的某处半径，m

εr——颗粒相对介电常数

μg——气体动力黏度，kg/(m·s)

ε0——真空介电常数，F/m

FEr——电场力

ηd——某粒径颗粒的理论除尘效率

ηt——所有粒径颗粒的理论除尘效率

Up——端口电压，V

Fg——重力，N

y1——颗粒在y轴方向的总位移，m

ρg——气体密度，kg/m3

T——温度，K

vx——颗粒在x轴方向的速度，m/s

M——气体分子摩尔质量

ρp——颗粒密度，kg/m3

yc——荷电过程中颗粒在y轴方向的位移，m

g——重力加速度，N/kg

r0——阴极线的半径，m

r1——以阴极线为圆心的某处半径，m

R——气体普适常数

yr——匀速过程颗粒在y轴方向的位移，m

ta——颗粒加速时间，s

p——压力，Pa

ya——加速过程颗粒在y轴方向的位移，m

tm——颗粒运动时间，s

vr——电场中颗粒相对速度，m/s

qV——气体体积流量，m3/s

v——颗粒速度，m/s

ρd,l——某粒径颗粒出口质量浓度，kg/m3

S——颗粒截面积，m2

m——颗粒质量，kg

vp,y——颗粒在y轴方向的绝对速度，m/s

Er——半径r处的场强，V/m

d——颗粒直径，m

Vr——半径r处的气流速度，m/s

Fd——拽力，N

vy——颗粒在y轴方向的相对速度，m/s

ρin——颗粒入口质量浓度，mg/m3

nd,i——粒径为d的颗粒百分数

高温除尘是煤炭梯级利用热电联产、整体煤气化联合循环发电以及增压循环流化床等洁净煤技术必须攻克的关键问题之一[1]。研究表明，在350～700 ℃内高温线管式静电除尘器的颗粒脱除效率可达99.6%，说明这是一种有潜力的高温除尘技术[2]。

关于高温(400 ℃及以上)静电除尘技术的理论研究极少，文献中的分析模型大多聚焦于气体温度低于200 ℃的除尘器，即采用Kaptzov假设，根据Peek公式计算阴极表面场强，获得放电空间的场强与电荷分布[3-5]，计算颗粒的饱和荷电量[6-8]，进而得出颗粒的驱进速度，采用Deutch公式获得除尘效率[9-11]。研究表明，高温环境与常规温度下的电晕放电有较大差异，常规温度下的相关放电理论不能直接应用[12-13]。另外，高温线管式静电除尘器内的电场分布不均会导致不同空间位置颗粒的驱进速度存在较大差异[14]，不宜再采用Deutch公式计算除尘效率，因此有必要对高温静电除尘过程进行理论研究。文献[14]给出了高温线管式静电除尘器内电晕放电的解析方法，笔者针对Deutch公式不再适用的局限，通过分析荷电颗粒在气相流场耦合电场中的受力情况，计算出颗粒在有效除尘空间内的运动轨迹，判断颗粒在收尘极上的落点是否在有效收尘面积内，进而推导出颗粒的捕集效率表达式，为高温线管式静电除尘器内颗粒捕集过程提供了一种新的解析方法。

1 理论模型

1.1 实验装置

实验装置如图1所示，由鼓风机将空气吹入除尘实验系统，经过二级加热装置，将气体加热至工况所需温度。在第一级加热装置入口处，安装有电磁振动给料机，通过调节振动频率控制进入气流的颗粒质量浓度，以模拟高温含尘烟气。除尘器本体直径为0.2 m、高为2 m，有效除尘高度为1.7 m。所有加热元件均由可编程的温度控制仪进行控制，实验工况中气体体积流量设为8 m3/h[2]。

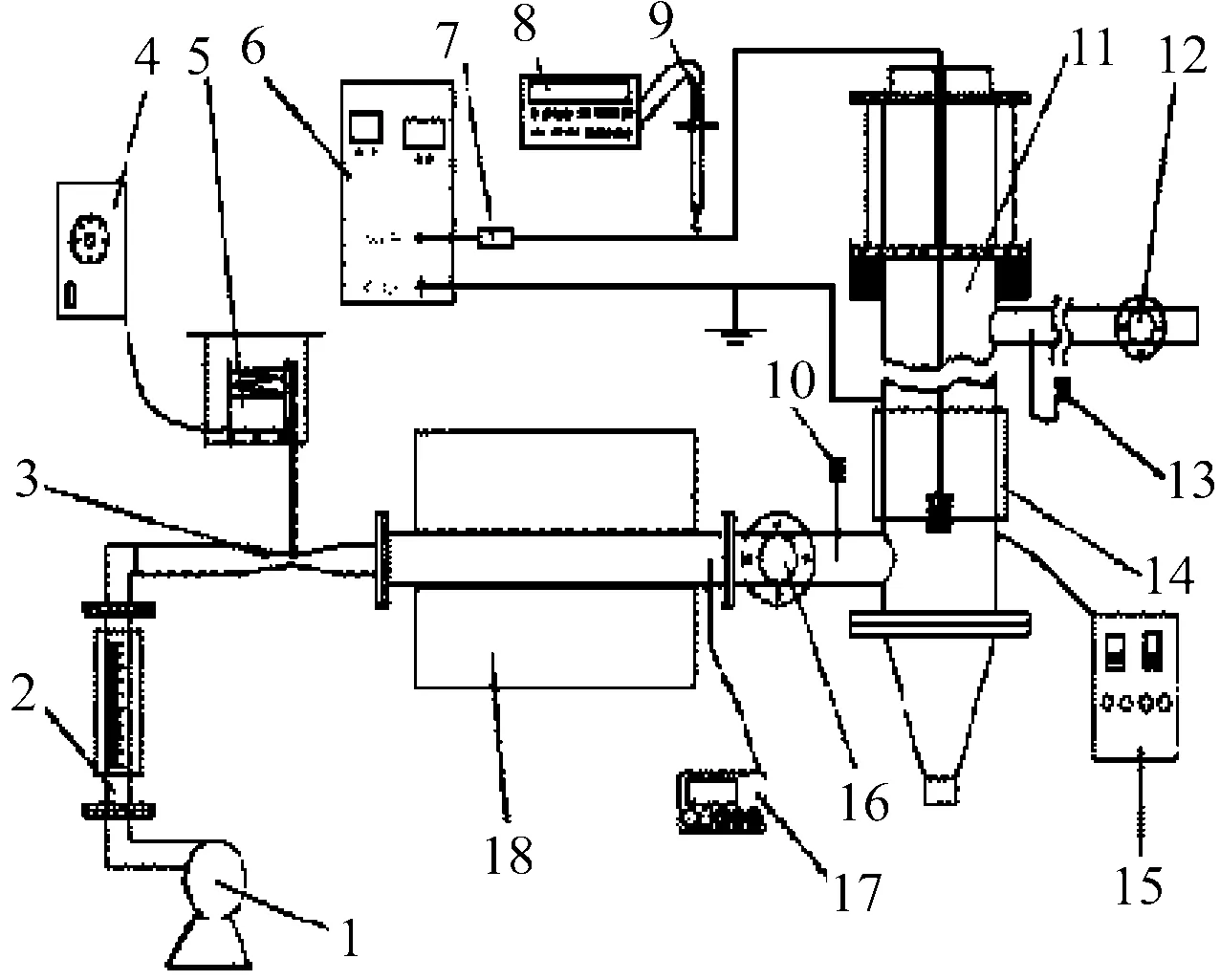
1—鼓风机； 2—气体流量计； 3—文丘里管； 4—电磁振动调节器； 5—给料装置； 6—负高压电源； 7—保护电阻； 8—6514静电计； 9—高压探测棒； 10—热电偶； 11—除尘器； 12—飞灰质量浓度出口采样口； 13—热电偶； 14—套管加热器； 15—可编程温控仪1； 16—飞灰质量浓度入口采样口； 17—可编程温控仪2； 18—管式加热炉

1.2 颗粒受力分析

计算工况中气流速度较小(平均流速为0.15～0.24 m/s)，质量流量恒定，颗粒为球形，可合理简化受力分析，着重考虑重力、浮力、拽力和电场力对颗粒的作用。由图1可知，颗粒进入除尘装置，运动一段距离后进入有效除尘空间。为模拟实验工况，得到颗粒在进入有效除尘空间的瞬间运动状态，先分析颗粒在进入电场前的运动情况，受力分析如图2(b)所示。

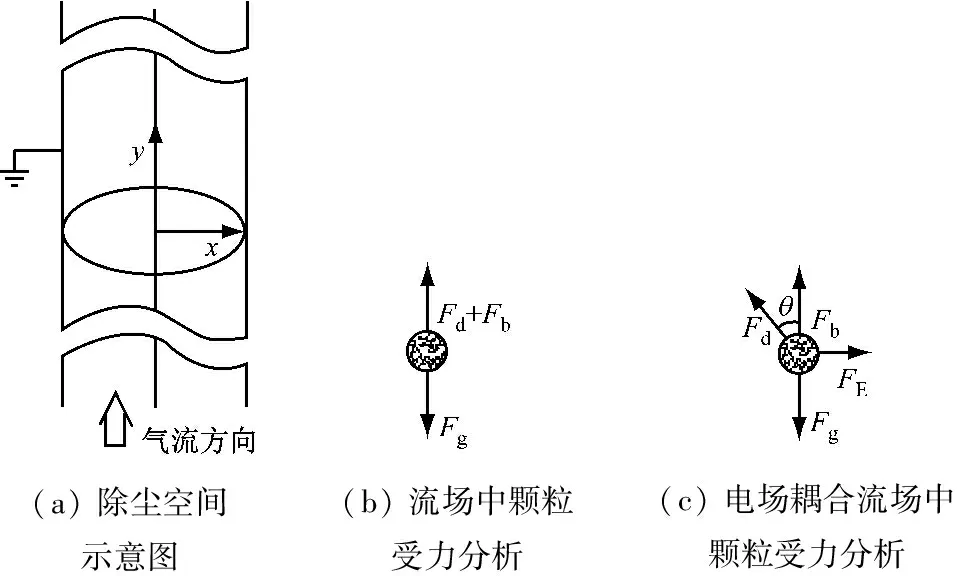
(a)除尘空间示意图(b)流场中颗粒受力分析(c)电场耦合流场中颗粒受力分析

图2 除尘器结构及颗粒受力分析图

Fig.2 Structural diagram of the precipitator and force analysis of a particle

颗粒的运动方程为：

(1)

(2)

(3)

(4)

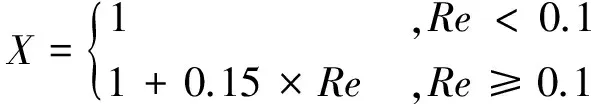
(5)

(6)

当颗粒处于平衡状态时，其在y轴方向的相对速度为：

(7)

颗粒进入电场后，除浮力、重力和拽力外，还受到x轴方向的电场力，受力分析如图2(c)所示，其运动方程为：

(8)

(9)

(10)

颗粒在电场中达到平衡状态时，在x轴方向的相对速度为：

(11)

颗粒在x轴方向的相对速度即为其驱进速度。

1.3 颗粒的捕集效率

在线管式静电除尘器中，放电空间内的电场分布是极不均匀的[14]。由式(9)和式(11)可知，颗粒的驱进速度分布也极不均匀，多依奇效率计算公式不再适用。因此需分析颗粒的运动轨迹，考察每个颗粒的捕集或逃逸情况，进而计算除尘效率。假设颗粒的运动情况满足以下条件：颗粒经短暂加速后受力达到平衡状态，并保持该状态直至被捕集或逃逸[11]；忽略颗粒间的碰撞、团聚以及惯性拦截作用；颗粒被捕集后不反弹；颗粒在除尘器入口截面上均匀连续分布；颗粒进入电场后均可荷电至饱和状态；颗粒运动对气流的扰动作用可忽略不计。

颗粒进入电场后，经历荷电、加速，而后保持平衡状态，直至被捕集或逃逸，在有效除尘空间内的总运动时间为三者之和。当荷电时间为时间常数的10～20倍时，可认为荷电已饱和，笔者取荷电时间t为时间常数的15倍。荷电时间常数可根据颗粒所处位置的离子密度获得。荷电后至平衡状态前经历的加速时间由下式近似计算：

(12)

达到平衡状态后运动至收尘极所需时间为：

(13)

文献[11]的研究表明，高温线管式静电除尘器内的气流速度以阴极线和阳极管为边界，且以阴极线为中心呈对称分布，其表达式为：

(14)

结合式(7)，可计算颗粒荷电前在y轴方向上的绝对速度：

vp,y=Vr-vy

(15)

假设荷电过程中颗粒在y轴方向上的速度变化忽略不计，运动时间为荷电时间，则该过程中颗粒在y轴方向上的位移yc为：

yc=vp,y×t

(16)

荷电饱和后，颗粒经加速至受力平衡状态，该时间段内颗粒在y轴方向的位移ya为：

ya=vp,y×ta

(17)

在颗粒达到平衡状态至其运动到收尘极的时间段内，颗粒在y轴方向上的位移yr为：

yr=vp,y×tm

(18)

进入有效除尘空间后，颗粒在y轴方向上的总位移y1为：

yl=yc+ya+yr

(19)

分别计算颗粒在x轴和y轴方向的位移。若到达收尘极时颗粒在y轴方向的位移小于有效收尘面积的高度，则认为颗粒被捕集，反之认为颗粒逃逸。通过设置合适的步长，在异极距空间内寻找颗粒被捕集的区域，可得到除尘效率。经分析得知，颗粒在进入电场的瞬间，其位置处于两电极的中间时逃逸的潜力最大。如图3所示，假设进入电场的瞬间，颗粒位置在r0～r1和r2～R0的空间内时，颗粒将被捕集。由于颗粒连续均匀分布，则被捕集区域的面积占总截面面积的比值即为除尘效率：

(20)

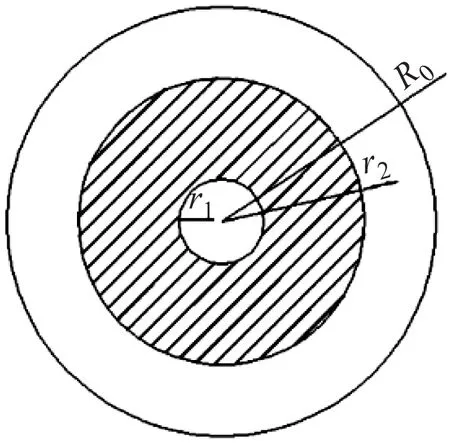
图3 除尘器横截面的颗粒分布

不同粒径的颗粒荷电量以及受力情况各不相同，式(20)仅适用于计算某一粒径颗粒的除尘效率。采用马尔文粒度分析仪测出粒径分布，即可计算总除尘效率。计算过程中使用的粒径分布数据以及除尘效率实验结果均引自文献[1]。假设颗粒进入电场瞬间总质量浓度为ρa，粒径为d的颗粒百分数为nd,i，经过有效除尘空间后，出口处该颗粒的质量浓度ρd,l为：

ρd,l=ρa×nd,i×(1-ηd)

(21)

利用式(21)计算每个粒径颗粒的除尘效率，结合各个粒径颗粒的权重，得到除尘器出口截面上的颗粒质量浓度，进而计算除尘总效率：

(22)

2 计算结果与讨论

2.1 除尘效率计算

为验证计算结果的准确性，图4给出了各温度下除尘效率的计算与实验结果。为与文献[15]进行对比，选择与其相同的工况进行计算。2种计算模型得到的结果与实验结果的相对误差如表1所示。在文献[15]的计算模型中，不考虑阴极线对气体流动的边界作用。在笔者的计算模型中，气流速度参照Dastoori等[11]的研究结果，即认为阴极线和收尘极同为气流的边界，气流速度在两边界的空间内呈抛物线分布。

由图4和表1可知，采用文献[15]与笔者提出的模型进行计算，其结果在大部分工况下与实验结果符合较好。端口电压高于15 900 V时，与实验结果相比，计算结果的相对误差小于10%。相对误差随端口电压的提高而减小，如温度为350 ℃时，端口电压从14 287 V提高至20 166 V。采用笔者的模型时，相对误差由约13.5%减小至约1.7%；采用文献[15]中的模型时，相对误差从约11.3%减小至约1.6%。温度为350 ℃和500 ℃时，笔者的计算结果与文献[15]的计算结果非常接近。温度为620 ℃和700 ℃时，笔者的计算结果相对误差略小。温度从350 ℃升高至700 ℃时，气流平均速度从0.15 m/s增大至0.24 m/s，说明当气流速度大于0.2 m/s时，阴极线对气流速度分布的边界作用开始显现，把阴极线与收尘极同时作为气流的边界更加符合实际情况。

2.2 驱进速度分析

以620 ℃的工况为例，分析相关参数对颗粒驱进速度的影响以及颗粒在除尘空间内的运动情况。图5为10 μm颗粒的驱进速度与端口电压的对应关系。除尘器结构不变时，在火花击穿之前，放电空间同一位置处的场强随着端口电压的提高而增强。因此，相同直径、相同空间位置颗粒的驱进速度与端口电压呈正相关。端口电压和颗粒直径相同时，颗粒距离阴极线越近，其驱进速度越大。

图6(a)给出了端口电压为17 310 V时除尘器异极距空间内的电场分布，图6(b)为该电压下颗粒的驱进速度与其直径的关系。笔者的计算结果与文献[15]中计算得到的驱进速度分布差异较大，这是因为2种计算模型采用的气体流场边界不同，导致气流速度分布不同，从而使得颗粒的驱进速度也不相同。从场强分布来看，在阴极线附近，场强约为3.4×106V/m，在阳极管附近，场强仅约为0.1×105V/m。这表明当颗粒直径相同时，颗粒在阴极附近处所受的电场力远大于阳极管附近的电场力，根据式(11)，颗粒的驱进速度也应如此。因此，颗粒距离阴极线越远，驱进速度越小，更符合实际情况。取1个计算工况为例，颗粒直径为10 μm时，驱进速度在阴极线附近约为20 m/s，同颗粒的驱进速度在阳极管附近约为0.06 m/s。空间位置一定时，颗粒饱和荷电量随颗粒直径的增大而增加，因此，颗粒直径越大，电场力对其拉动作用越大，使其能更快速地向收尘极运动。

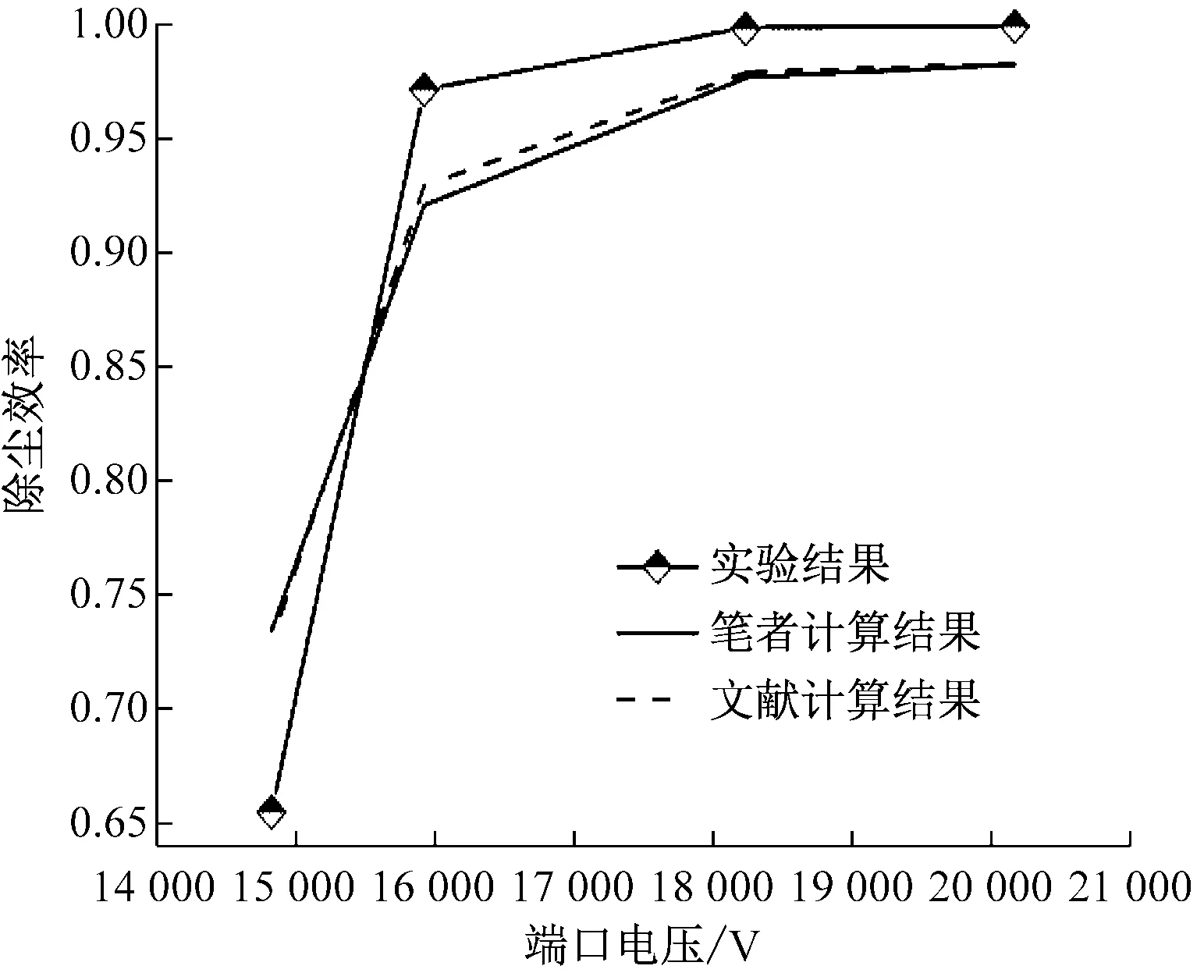
(a) 350 ℃, ρin=974 mg/m3

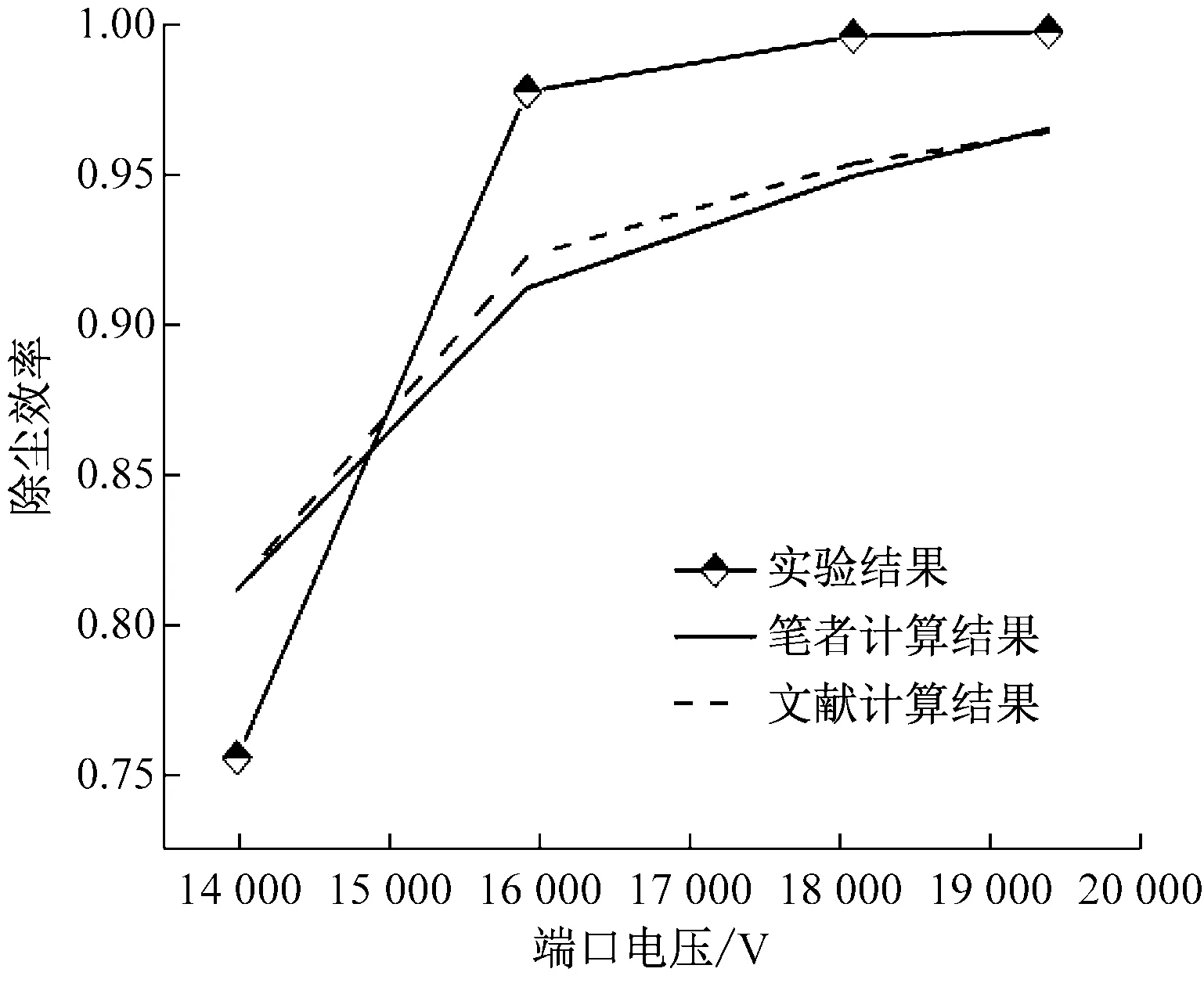
(b) 500 ℃, ρin=1 214 mg/m3

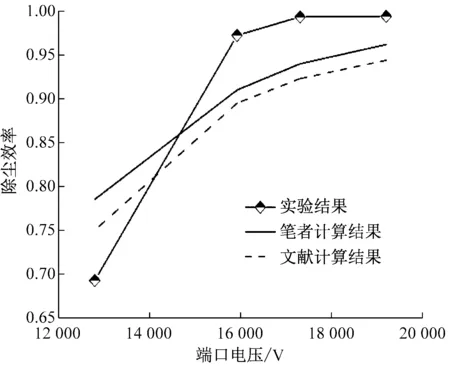
(c) 620 ℃, ρin=874 mg/m3

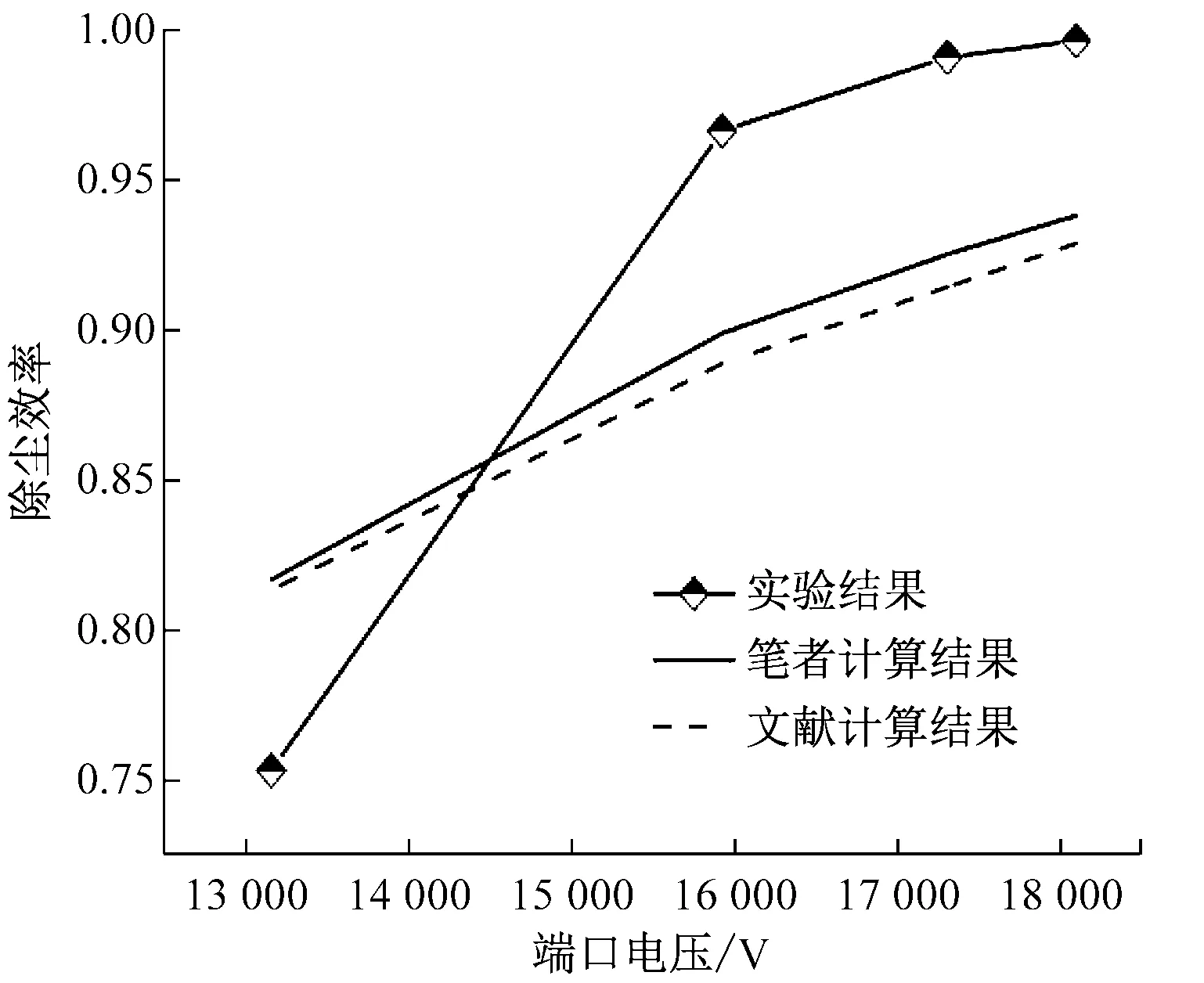
(d) 700 ℃, ρin=918 mg/m3

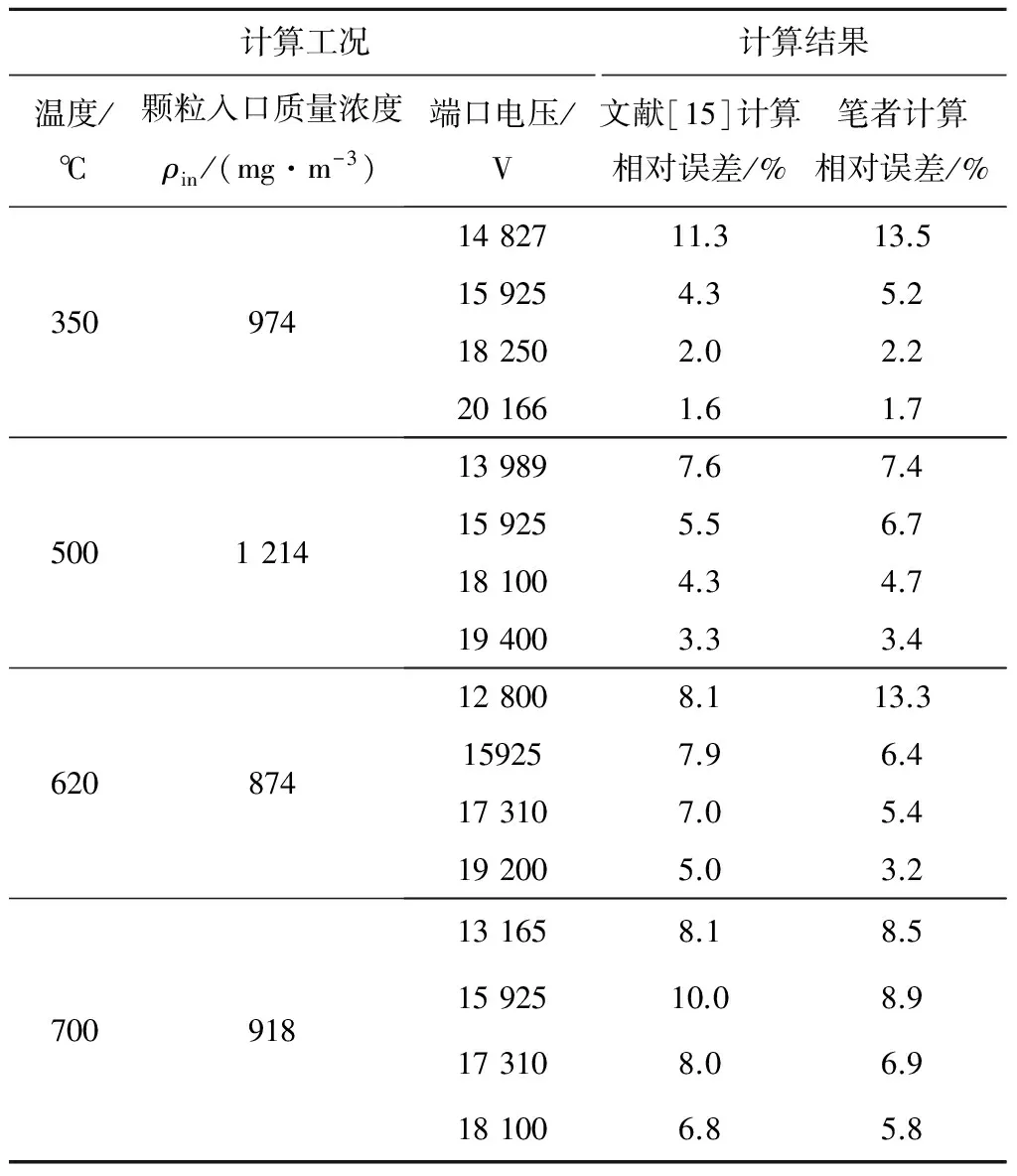
表1 计算与实验结果的相对误差

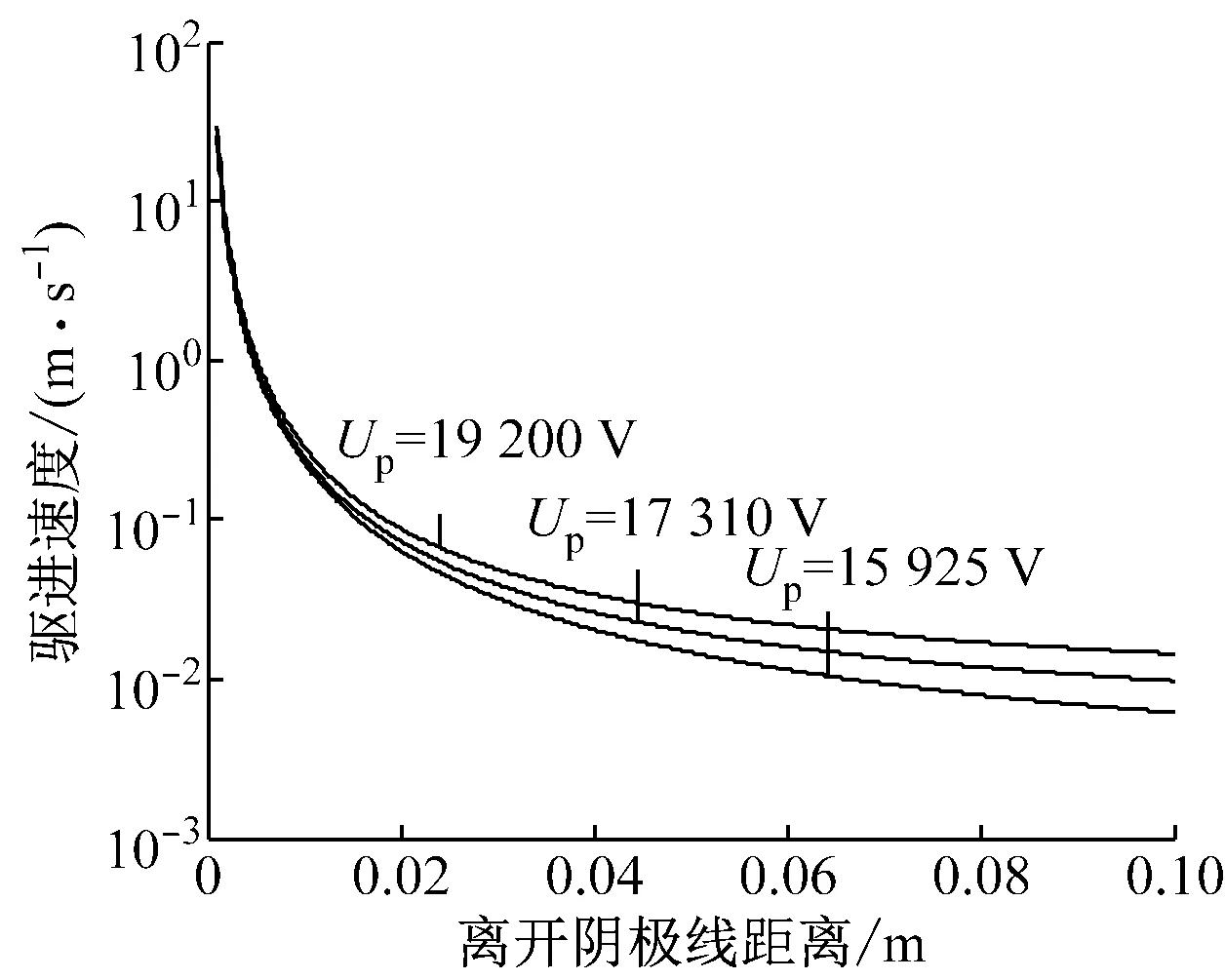
图5 端口电压对颗粒驱进速度的影响

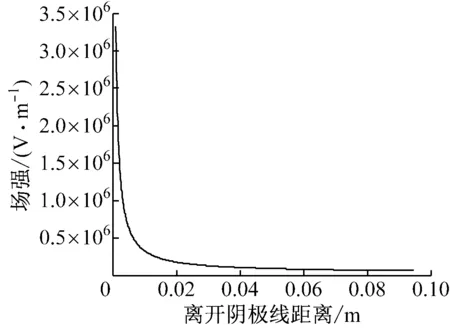
(a) 场强分布

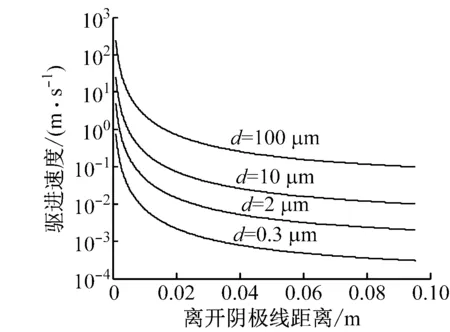
(b) 驱进速度分布

2.3 颗粒的运动分析

图7给出了不考虑颗粒影响下的气体流速。由于气体流速以阴极线为中心呈对称分布，故仅截取阴极线到阳极管任意截面上的气流速度分布。由图7可知，在两电极中间某个位置处气流速度达到最大，而在阴极线和阳极管表面气流速度为0。根据式(14)，颗粒在气流方向上的绝对速度也在两电极中间某个位置达到最大，这部分颗粒最有可能逃逸。

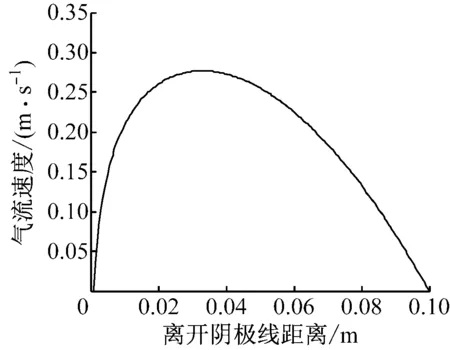
图7 620 ℃时除尘器内的气流速度分布

图8为颗粒在y轴方向上的位移与端口电压的对应关系。对具有相同直径和空间位置的颗粒而言，当端口电压较大时，电场力在x轴方向上对颗粒的拉动作用较大，颗粒在更短的时间内可到达阳极管，在y轴方向上的运动时间减少，在该方向的位移随之减小，对应的除尘器高度也减小。以10 μm的颗粒为例，当端口电压为19 200 V时，在y轴方向的最大位移约为0.42 m，说明除尘高度仅需大于0.42 m，除尘效率即可达到100%。当端口电压为15 925 V时，在y轴方向上的最大位移约为0.86 m。为获得与端口电压为19 200 V时相同的除尘效率，除尘高度需增大一倍多。因此，在不引起火化击穿的前提下，可通过适当提高端口电压，以达到减小除尘器高度的目的。

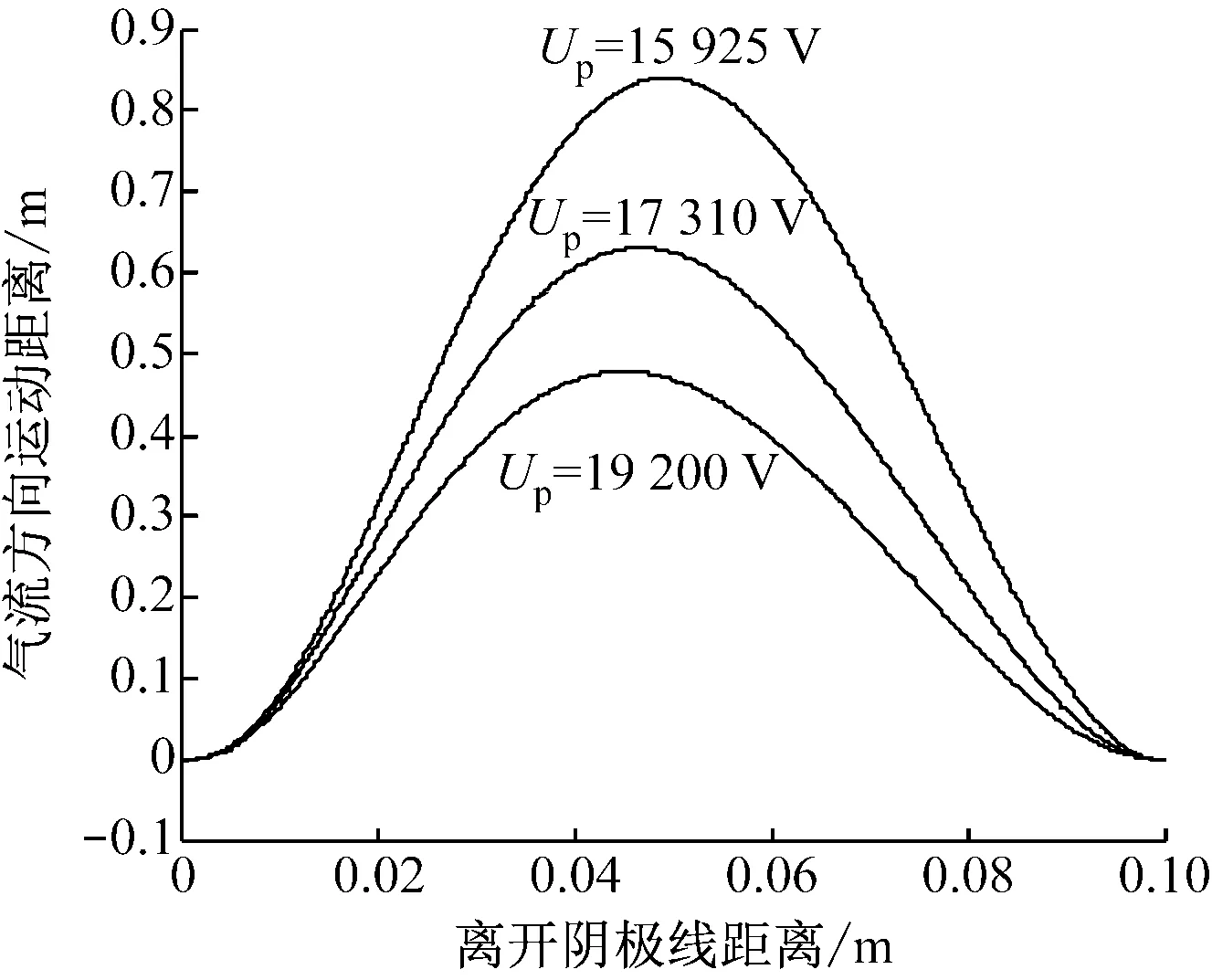
图8 620 ℃时不同端口电压下颗粒在气流方向上的位移

图9为端口电压不变(Up=17 310 V)时颗粒在y轴方向上的位移与颗粒直径的对应关系。颗粒直径相差较大时，在y轴方向的位移也有较大差别。为详细描述颗粒直径对位移的影响，根据颗粒直径将计算结果分成2组，如图9(a)和图9(b)所示。当颗粒直径分别处于亚微米和微米量级时，在y轴方向的位移也存在数量级的差别，故图9(a)采用对数坐标。当直径大于10 μm时，颗粒在y轴方向的位移相差不大，故图9(b)采用线性坐标。当直径为0.3 μm，初始位置在距阴极线约0.05 m处，当颗粒被捕集时，其在y轴方向的最大位移达到约20 m，实验装置的有效除尘高度为1.7 m，这部分颗粒将逃逸。同是直径为0.3 μm的颗粒，距阴极线约0.008 m或距阳极管约0.009 m时，其在y轴方向的位移约为1.6 m，颗粒将被捕集。将步长设置为0.000 1m，计算每个步长内颗粒在y轴方向的位移，并与有效除尘高度进行比较，即可确定颗粒的逃逸边界，进而计算该粒径颗粒的除尘效率。对直径为6 μm的颗粒而言，其在y轴方向的最大位移小于1.7 m，该粒径的除尘效率达到100%。由此推断，总除尘效率随着亚微米颗粒权重的增加而降低。

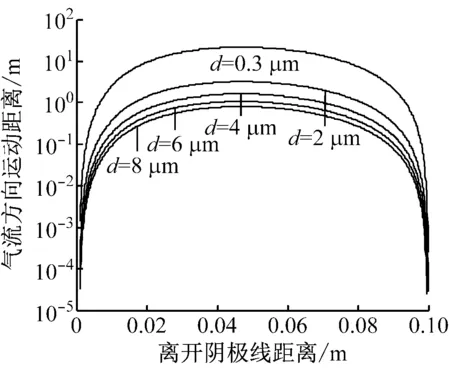
(a) d为0.3 ～ 8 μm

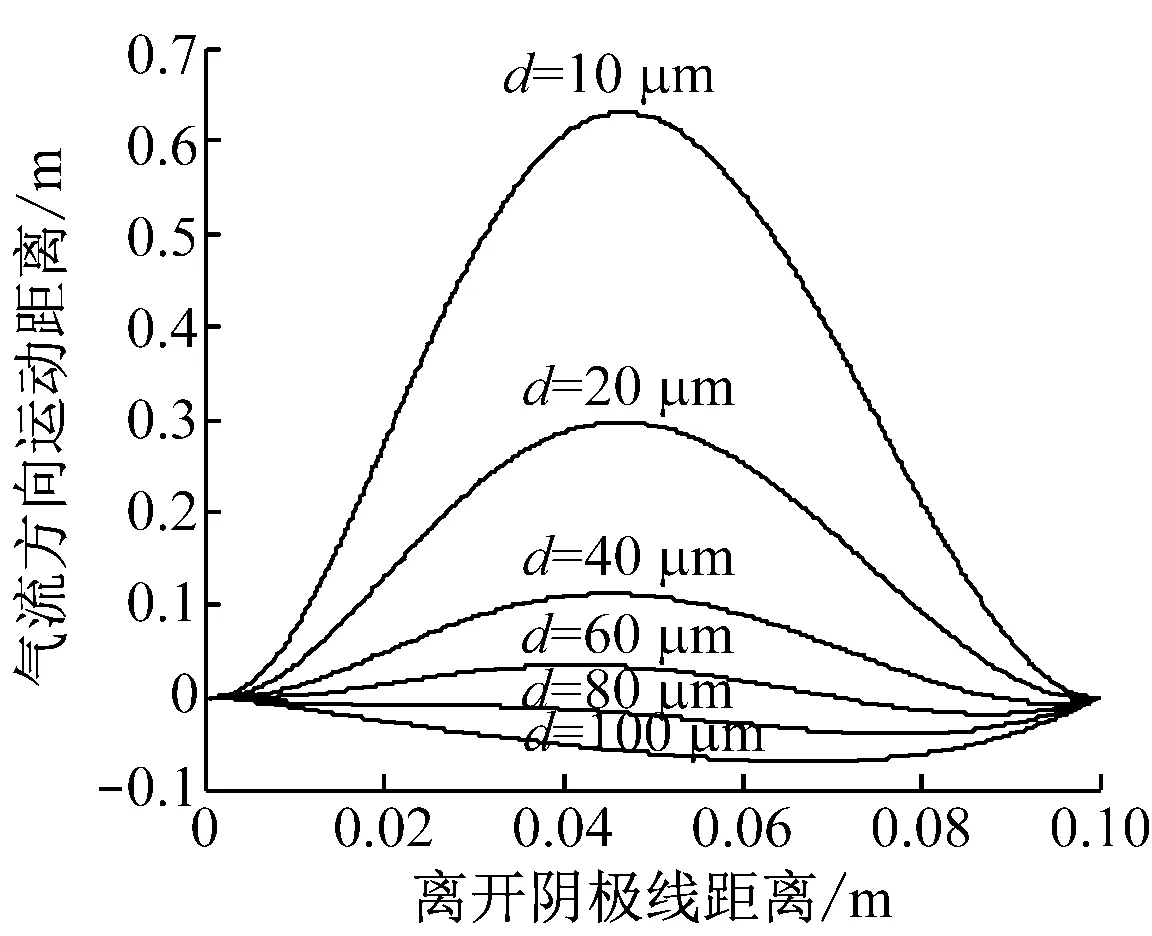
(b) d为10 ～ 100 μm

由图9(a)可知，在靠近阴极线和阳极管时，颗粒在y轴方向的位移较小，且近似呈对称分布。这是因为在两电极附近时，颗粒受气流速度的影响，在y轴方向的绝对速度略小，位移也减小。

在阴极线附近时，颗粒受电场力的影响，其在x轴方向的速度远大于其他位置，将迅速被捕集，这部分颗粒在y轴方向的运动时间缩短。在阳极管附近时，虽然颗粒在x轴方向的速度最小，但其距收尘极最短，节省了颗粒的运动时间。因此，靠近两电极的颗粒最容易被收集。对于具有相同空间位置的颗粒，其在y轴方向的位移随着粒径的增大而减小。这是因为颗粒在x轴方向的速度随粒径的增大而增大，与收尘极的距离相同时，颗粒的运动时间缩短。此外，颗粒直径越大，重力作用越大，其在y轴方向的速度越小。当颗粒直径很大时(>80 μm)，在重力作用下即可被捕集。

3 结 论

(1) 温度为350～700 ℃内，端口电压高于15 900 V，计算结果的最大相对误差不超过9%，相对误差随着端口电压的提高而减小。当气流速度大于0.2 m/s时，阴极线对气流速度分布的边界作用开始显现，把阴极线与收尘极同时作为气流的边界更符合实际情况。

(2) 对相同直径的颗粒而言，当其初始位置不一样时，驱进速度相差很大。提高端口电压，可减小除尘器高度。以10 μm的颗粒为例，端口电压为15 925 V时，除尘效率达到100%，对应的除尘器高度约为0.86 m，而端口电压为19 200 V时，除尘器高度约为0.42 m。总除尘效率随着亚微米颗粒权重的增大而降低。直径相同时，空间位置靠近两电极的颗粒更容易被捕集。

参考文献：

[1] 唐虹云, 蒋伟康, 钟振茂, 等. 燃气轮机发电机组余热锅炉低频噪声机理研究[J].动力工程学报, 2014, 34(12): 978-984.

TANG Hongyun, JIANG Weikang, ZHONG Zhenmao, et al. Research on formation mechanism of low frequency noise in a heat recovery steam generator[J].JournalofChineseSocietyofPowerEngineering, 2014, 34(12): 978-984.

[2] XIAO Gang, WANG Xihui, YANG Guang, et al. An experimental investigation of electrostatic precipitation in a wire-cylinder configuration at high temperatures[J].PowderTechnology, 2015, 269: 166-177.

[3] FARNOOSH N, ADAMIAK K, CASTLE G S P. 3-D numerical analysis of EHD turbulent flow and mono-disperse charged particle transport and collection in a wire-plate ESP[J].JournalofElectrostatics, 2010, 68(6): 513-522.

[5] FARNOOSH N, ADAMIAK K, CASTLE G S P. 3-D numerical simulation of particle concentration effect on a single-wire ESP performance for collecting poly-dispersed particles[J].IEEETransactionsonDielectricsandElectricalInsulation, 2011, 18(1): 211-220.

[6] ZHAO Haibo, ZHENG Chuguang. A stochastic simulation for the collection process of fly ashes in single-stage electrostatic precipitators[J].Fuel, 2008, 87(10/11):2082-2089.

[8] LONG Zhengwei, YAO Qiang. Evaluation of various particle charging models for simulating particle dynamics in electrostatic precipitators[J].JournalofAerosolScience, 2010, 41(7): 702-718.

[9] AL-HAMOUZ Z, EL-HAMOUZ A, ABUZAID N. Simulation and experimental studies of corona power loss in a dust loaded wire-duct electrostatic precipitator[J].AdvancedPowderTechnology,2011, 22(6):706-714.

[10] GUO Baoyu, YANG Siyuan, XING Mao, et al. Toward the development of an integrated multiscale model for electrostatic precipitation[J].Industrial&EngineeringChemistryResearch, 2013, 52(33): 11282-11293.

[11] DASTOORI K, KOLHE M, MALLARD C, et al. Electrostatic precipitation in a small scale wood combustion furnace[J].JournalofElectrostatics, 2011, 69(5): 466-472.

[12] XIAO Gang, WANG Xihui, ZHANG Jiapeng, et al. Characteristics of DC discharge in a wire-cylinder configuration at high ambient temperatures[J].JournalofElectrostatics,2014, 72(1): 13-21.

[13] XIAO Gang, WANG Xihui, ZHANG Jiapeng, et al. Current analysis of DC negative corona discharge in a wire-cylinder configuration at high ambient temperatures [J].JournalofElectrostatics,2014, 72(2): 107-119.

[14] WANG Xihui, NI Mingjiang, XIAO Gang, et al. An analytical method for DC negative corona discharge in a wire-cylinder device at high temperatures[J].JournalofElectrostatics, 2014, 72(4): 270-284.

[15] 杨光，肖刚，倪明江,等. 高温线管式静电除尘过程三维模拟[J].热力发电，2017，46(5)：43-49.

YANG Guang, XIAO Gang, NI Mingjiang, et al. 3D numerical simulation of particles collection in a high-temperature wire-cylinder electrostatic precipitator [J].ThermalPowerGeneration，2017，46(5)：43-49.