基于自适应量子灰狼算法的锅炉NOx预测模型

牛培峰， 史春见， 刘 楠， 马云鹏， 吴志良， 李进柏

(燕山大学 工业计算机控制工程河北省重点实验室，河北秦皇岛 066004)

氮氧化物(NOx)主要在燃烧过程中产生，是一种危害人体健康和破坏大气环境的有毒污染物[1]。我国50%以上排放的NOx源于火电厂燃煤锅炉[2]。因此，建立有效的火电厂燃煤锅炉NOx排放特性预测模型变得至关重要。

由于锅炉的NOx排放量与其影响因素之间存在复杂的非线性关系，根据传统机理建模方法建立的数学模型会导致NOx排放量发生偏差[3-6]。因此，笔者采用近些年工程领域内建模与控制问题中常用的神经网络建模。牛培峰等[3,7]研究了基于支持向量机和果蝇优化算法的循环流化床锅炉NOx排放特性模型和基于GSA-SVM的循环流化床锅炉NOx排放特性模型；牛培峰等[6]提出基于风驱动算法的锅炉NOx排放优化模型，建立了风驱动算法的预测模型，该模型具有较高的准确性和稳定性。但常规神经网络的不足之处是计算量大、迭代训练时间偏长、训练速度慢、泛化能力较差和易陷入局部极小点等[8-11]。为了解决这些问题，笔者提出了通过自适应量子灰狼算法(AQGWO)来优化快速学习网(FLN)的综合建模方法[12-13]。

灰狼算法(GWO)是Mirjalili等[14]提出的新型启发式仿生群体智能优化算法。GWO具有原理简单、易于实现、参数调整少且不需要问题的梯度信息等优点，在函数优化方面，GWO在求解精度和稳定性上要明显优于粒子群算法(PSO)[9]、差分进化算法(DE)[10]和万有引力算法(GSA)，更适合用于优化FLN模型。但是在处理复杂的优化问题上，GWO与其他基于种群迭代的智能搜索算法相似，也存在易陷入局部最优且收敛精度低的情况。为此，笔者提出了AQGWO，并利用其与PSO、 DE、基本GWO和鲸鱼算法(WOA)[15]对单峰、多峰等8个基准测试函数进行对比测试。结果表明，AQGWO的收敛速度最快，收敛精度最高。由于FLN模型过于依赖随机初始的阈值和输入权值，所以采用AQGWO对FLN模型进行参数优化。为了验证该模型的准确性和有效性，将该模型与基本GWO、PSO、WOA、DE的FLN模型和基本FLN模型进行比较，发现AQGWO-FLN模型的性能最好，具有更高的预测精度和更强的泛化能力，因而能准确有效地预测锅炉NOx排放。

1 快速学习网

快速学习网(FLN)是李国强[13]提出的一种新型前馈双并联神经网络，与极端学习机[11]不同的是，其输出层不只接收来自隐藏层神经元的信息，还直接从输入层接收相关信息。该模型是一种隐藏层到输出层(非线性)和输入层到输出层(线性)的组合模型，FLN的结构如图1所示。

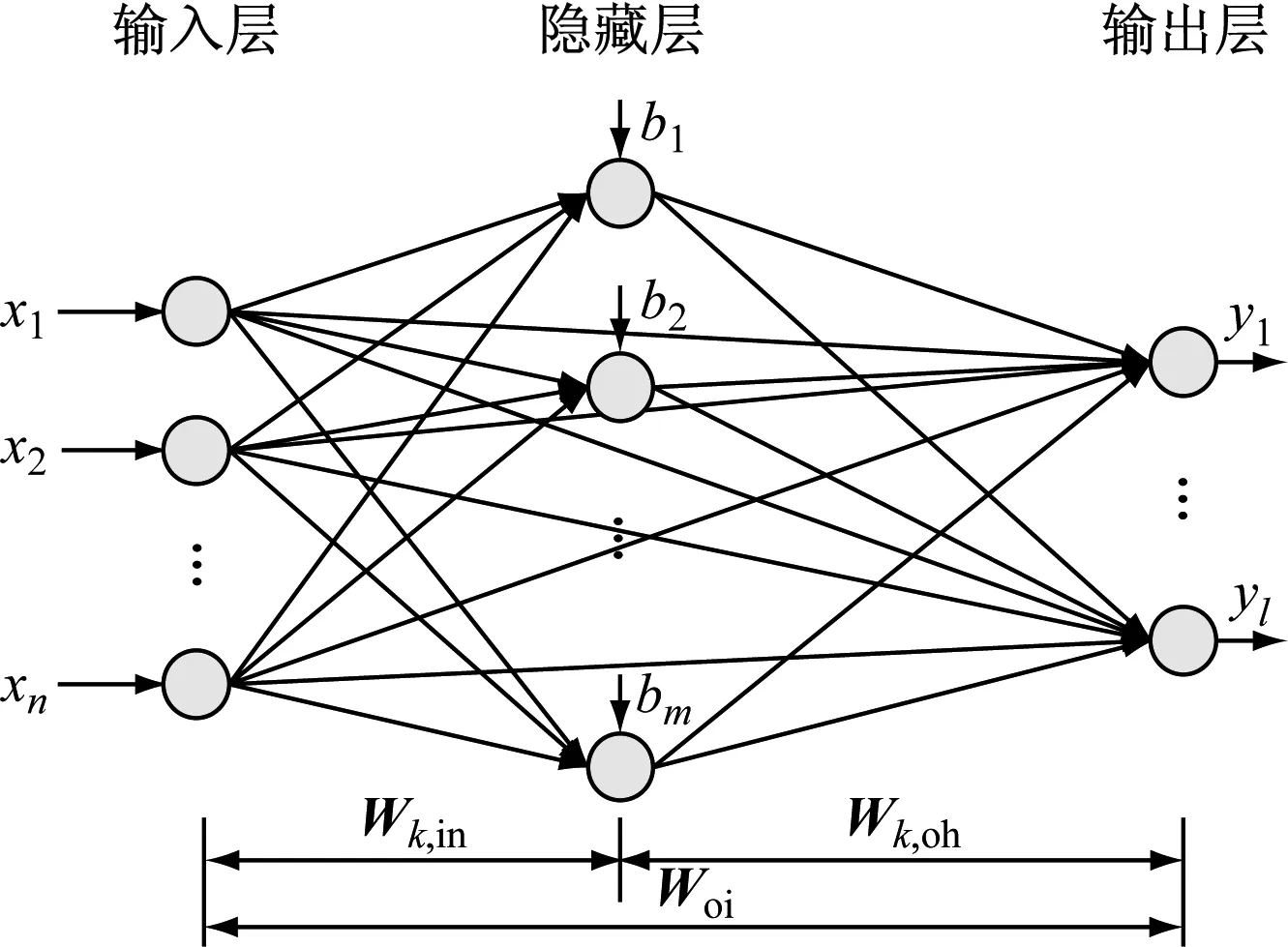
图1 快速学习网结构图

在N个实验样本中，假设隐藏层神经元的个数设为m，g(x)为隐藏层激励函数，则FLN的数学模型为：

(1)

xj=[xj1,xj2,…,xjn]T,xj∈Rn

(2)

yj=[yj1,yj2,…,yjl],yj∈Rl

(3)

式中：yj为第j个样本的第l维输出向量，j=1,2,…,N；xj为第j个样本的第n维输入向量；Woi为输入层和输出层之间的连接权值矩阵；Wk,oh为第k个隐藏层神经元和输出层之间的连接权值矩阵，k=1,2,…,m；Wk,in为输入层和第k个隐藏层神经元之间的连接权值矩阵；bk为第k个隐藏层神经元的阈值；l为输出层的节点个数。

式(1)可表示为矩阵形式：

(4)

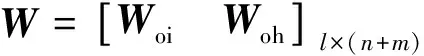
(5)

(6)

式中：X为输入矩阵；Y为期望输出矩阵；W为输出层权值矩阵；G为隐藏层输出矩阵；Woh为隐藏层和输出层之间的连接权值矩阵。

式(4)可根据最小二乘范数解求得：

(7)

(8)

2 灰狼算法

2.1 灰狼算法

灰狼算法是为模拟自然界中灰狼群体的社会等级机制和捕食行为而提出的一种新型群体搜索方法，灰狼群体的社会等级机制如图2所示。

图2 灰狼种群等级制度示意图

由图2可以看出，α、β、δ和ω层是灰狼群体的社会等级，其中头狼为α，领导灰狼群体；下属狼为β，协助头狼α作出决策;普通狼为δ，由α和β指挥；底层狼为ω，由α、β和δ指挥。灰狼群体在头狼α的带领下捕获猎物，狼群通过气味等信息逐渐靠近并追踪猎物；在猎物位置确定后，包围猎物；包围圈逐渐缩小，攻击猎物。

在D维空间中，假设种群X=(X1,X2,…,XN)由N只灰狼组成，定义群体历史最优解、次最优解、第三最优解和其他个体分别为头狼α、下属狼β、普通狼δ和底层狼ω。描述灰狼逐渐接近并包围猎物时，第i只灰狼的位置定义为：

Xid(t+1)=Xpd(t)-Aid|CidXpd(t)-Xid(t)|

(9)

Aid=2a×r1-a

(10)

Cid=2×r2

(11)

a=2-t/tmax

(12)

式中：t为迭代次数；Xid为第i只灰狼在第d维上的位置，其中i=1,2,…,N，d=1,2,…,D；Xp为猎物的位置，Xp=(Xp1，Xp2，…，XpD)；r1、r2均为[0,1]内的随机变量；Aid、Cid和a均为收敛因子；tmax为最大迭代次数。

灰狼群体α、β和δ的位置(Xα、Xβ和Xδ)分别为：

(13)

(14)

式中:Xid(t+1)表示第i只灰狼在第d维的最终更新状态。

2.2 自适应量子灰狼算法

2.2.1 量子初始化种群

Syafaruddin等[16]指出，对基于种群迭代的群体智能优化算法来说，初始种群的好坏影响算法的全局搜索速度和解的质量，多样性较好的初始种群对于提高算法的寻优性能很有帮助。由于GWO采用的是随机初始化种群个体，因而初始群体的多样性难以得到保证，在一定程度上降低了算法的搜索效率。

针对GWO存在的缺陷，笔者提出了量子位Bloch球面坐标编码初始化种群。采用该算法改进后的GWO在收敛精度和收敛速度上得到了较大幅度的提升。

在量子计算中，量子位表示最小的信息单位，也称为量子比特，一个量子比特的状态可表示为：

|φ〉=cos(θ/2)|0>+ei1φsin(θ/2)|1〉

(15)

式中：|φ〉为量子态；φ为量子态在Bloch球面xy平面投影与x轴的夹角；θ为量子态与z轴的夹角；ei1φ为复数的指数表现形式。

φ和θ可确定Bloch球面上一点P，如图3所示[17]。

图3 量子比特的Bloch球面

由图3可知，任何量子比特都与Bloch球面上的一点对应，因此量子比特可转换为Bloch坐标：

|φ〉=[cosφsinθsinφsinθcosθ]T

(16)

直接采用量子比特的Bloch坐标作为编码，设pi为群体中第i个候选解，编码方案如下：

(17)

φij=2π×r3

(18)

θij=π×r3

(19)

式中：φij、θij分别为第i个候选解的第j维Bloch坐标对应角度；r3为[0,1]区间内的随机数；n为优化空间的维数；i=1,2,…,N，j=1,2,…,n；N为群体规模。

每个候选解对应空间的3个位置，分别为x解、y解和z解：

(20)

将候选解pi上第j个量子位的Bloch坐标记为 [xij,yij,zij]T，每个解空间第j维的取值范围为 [aj,bj]，由单位空间In=[-1,1]n映射到解空间的变换公式为：

(21)

式中：(Xij,x，Xij,y，Xij,z)为第i个候选解的第j维对应解空间坐标。

优化问题的每个候选解对应3个解，在所有3N个候选解中选择N个适应度值较小的个体作为初始群体。

这种编码方式能增加群体的多样性，扩展搜索空间的遍历能力，进而改善初始群体的质量，加快算法的收敛速度。

2.2.2 变异算子

GWO基于最优保存策略，在进化后期，由于所有群体中灰狼个体均逼近最优个体区域，使其损失了群体多样性，因而如果当前最优灰狼个体是局部最优解，算法就陷入局部最优，这也是群体智能优化算法的共同缺点。为了克服这种缺点，笔者对当前群体中最优灰狼个体进行多样性变异操作：

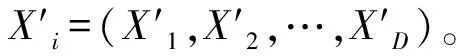
(22)

2.2.3 自适应惯性权值

为了增强GWO的局部开发能力，提高收敛精度和速度，笔者通过引入自适应惯性权值w对算法进行改进：

(23)

式中：w′和w″分别为惯性权值的最大值和最小值。

w随迭代次数t的增加而减小，在前期有利于全局探索，在迭代后期有利于局部寻优，提高了算法的收敛精度和速度。

改进后位置更新由式(13)改为式(24)：

(24)

AQGWO流程如下：

(1)初始化算法参数。群体规模大小为N，最大迭代次数为tmax，惯性权值的最大值为w′，惯性权值的最小值为w″。

(2)初始化群体位置。采用量子位Bloch球面对每个候选解进行编码，映射到优化问题的解空间，然后计算群体中每个个体的适应度值，根据适应度值的大小排序，最后选取N个个体作为初始群体，并选取适应度值最小的前3个个体位置，分别作为Xα、Xβ和Xδ，进行步骤4。

(3)计算N个个体的适应度值，选择适应度值最小的前3个个体位置，分别作为Xα、Xβ和Xδ。

(4)判断算法是否满足终止条件。若满足，输出最优灰狼个体，则算法结束；否则，执行下一个步骤。

(5)根据式(23)计算出惯性权值w，再根据式(24) 更新群体中每个灰狼个体的位置。

(6)判断当前位置未更新的迭代次数是否大于10。如果“是”，则按照式(22)进行变异，产生新的灰狼个体，否则不变。

(7)令t=t+1，返回步骤(3)。

3 AQGWO性能测试

为了比较的公平性，所有算法均在同一台电脑上运行，其配置为2.4GHz的Intel(R) Core(TM) i7-5500U CPU、8G内存和Windows 10操作系统，运行软件环境为Matlab R2012a。为了验证AQGWO的性能，将算法应用到8个经典的基准优化问题上(见表1)，其中f1～f5是高维的单峰基准测试函数，f6～f8是高维的多峰基准测试函数。

将AQGWO与DE、PSO、WOA、基本GWO进行了比较。将DE的比例系数F0设为0.6，交叉率Cr为0.85；PSO的学习因子c1、c2均为1.5；经过大量的仿真实验后，确定AQGWO惯性权重的最大值ω′和最小值ω″分别为1和0。DE、WOA、PSO、基本GWO和AQGWO这5种优化算法的其他相关参数设置相同，即初始化群体规模为40，迭代次数为1 000，实验独立运行次数为20。

将各个基准测试函数进行10、20和50维的测试，并给出在设定参数条件下各种优化算法最优值的平均值(Mean)和均方差(S.D.)，如表2所示。

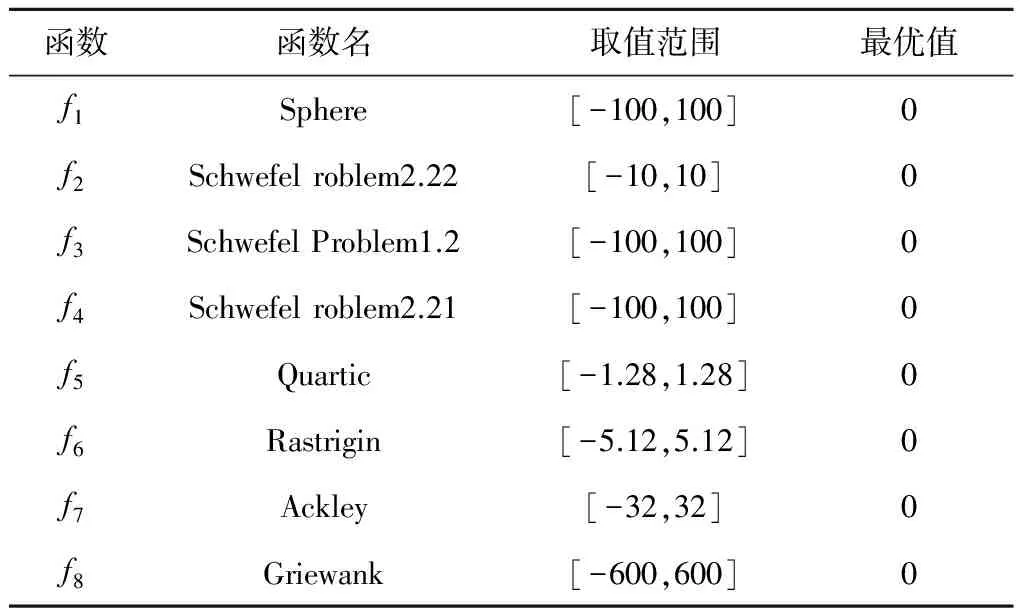
表1 8个基准测试函数

表2 基准测试函数测试4种不同算法的运行结果

由表2可知，在寻优精度方面，AQGWO均能寻到理论最优值(或非常接近理论最优值)，特别在f1～f4、f6和f8测试函数中能精确地寻到理论最优值，且方差为0；AQGWO在f6测试函数中找到最优值的精度比其他4个优化算法至少高1个数量级，方差至少高2个数量级；AQGWO在f7测试函数中找到最优值的精度比其他4个优化算法至少高1个数量级，且其方差为0。这说明对于绝大多数测试函数来说，与其他4个算法相比，AQGWO找到的最优解精度更高，方差更小。

4 AQGWO-FLN模型设计及仿真

4.1 数据样本

在循环流化床锅炉运行过程中，影响NOx排放的因素很多，因而在建模前需对循环流化床锅炉运行的各影响因素进行详尽分析。根据影响NOx排放质量浓度和各参数的关联程度来确定输入参数，应尽量选择与NOx排放质量浓度关联性强的参数，在可能的情况下应少选或不选间接影响的参数，这样可以提高NOx预测模型的计算精度和建模速度。根据此原则，并结合文献[18]，最终选择给煤机煤量、炉膛密相区上部平均床温、一次风体积流量、一次风温度、二次风总体积流量、二次风出口风温、石灰石粉输送电机电流、烟气氧气质量浓度、烟气温度、炉膛炉渣温度、SO2排放质量浓度和飞灰质量浓度等23个参数作为输入参数，NOx排放质量浓度作为输出参数，NOx排放质量浓度的计算详见文献[5]。

以某火电厂300 MW循环流化床锅炉[19-20]为研究对象，所用数据来自集散控制系统(DCS)现场，在其负荷分别为50%、70%和100%时通过集散控制系统以30 s的间隔时间采样一次，各采集50组工况运行数据，基本包括机组所有典型运行工况。从中随机选取120组样本(50%、70%和100%负荷下各40组)作为训练样本，剩下的30组样本作为该模型的测试样本。

4.2 模型建立及参数设置

由于FLN的输入权值和隐藏层阈值在初始化时是随机给定的，因而FLN模型的预测精度和泛化能力难以保证。为了克服这种缺点，应用AQGWO对FLN的隐藏层阈值和输入权值进行寻优，以目标函数适应度值最小为原则，达到最大迭代循环次数时结束循环，把AQGWO寻得的最优隐藏层阈值和输入权值代入FLN模型，AQGWO-FLN建立完成。

AQGWO设置的参数与前面保持一致。FLN的参数分别设成：隐藏层激励函数为“sigmoid”；隐藏层节点数为42；隐藏层阈值和输入权值寻优区间均为[-1,1]。该模型的优化目标函数为最小均方差，函数定义为：

(25)

式中：f为最小均方差函数;ρi,r为实际NOx排放质量浓度；ρi为模型预测所得NOx排放质量浓度。

具体的模型优化过程如图4所示。通过大量的仿真实验，确定该模型的循环迭代次数为200。先将120组训练样本代入FLN模型，根据适应度函数值选取最优隐藏层阈值和输入权值；再将30组测试样本输入FLN模型，得到测试样本预测值，并与实际值进行对比，以验证模型的预测能力。

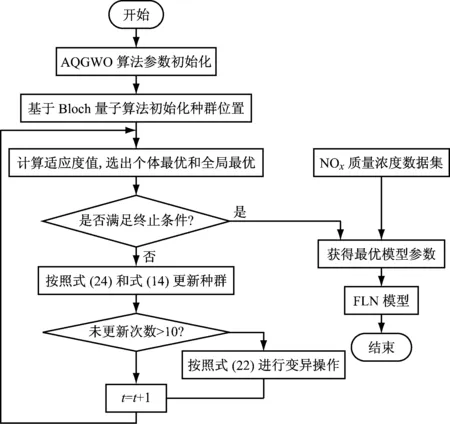
图4 采用AQGWO优化FLN结构参数的流程图

4.3 模型仿真结果及分析

仿真结果如图5和图6所示。图5为120组NOx排放质量浓度训练样本预测值与实际值的对比，发现除个别组的数据外，模型具有较高的拟合度。图6为30组NOx排放质量浓度测试样本预测值、FLN模型预测值与实际值的对比，发现AQGWO-FLN模型NOx排放质量浓度的预测值比FLN模型更加准确，且与实际值的拟合度非常高，能很好地预测NOx排放质量浓度，具有较强的泛化能力。

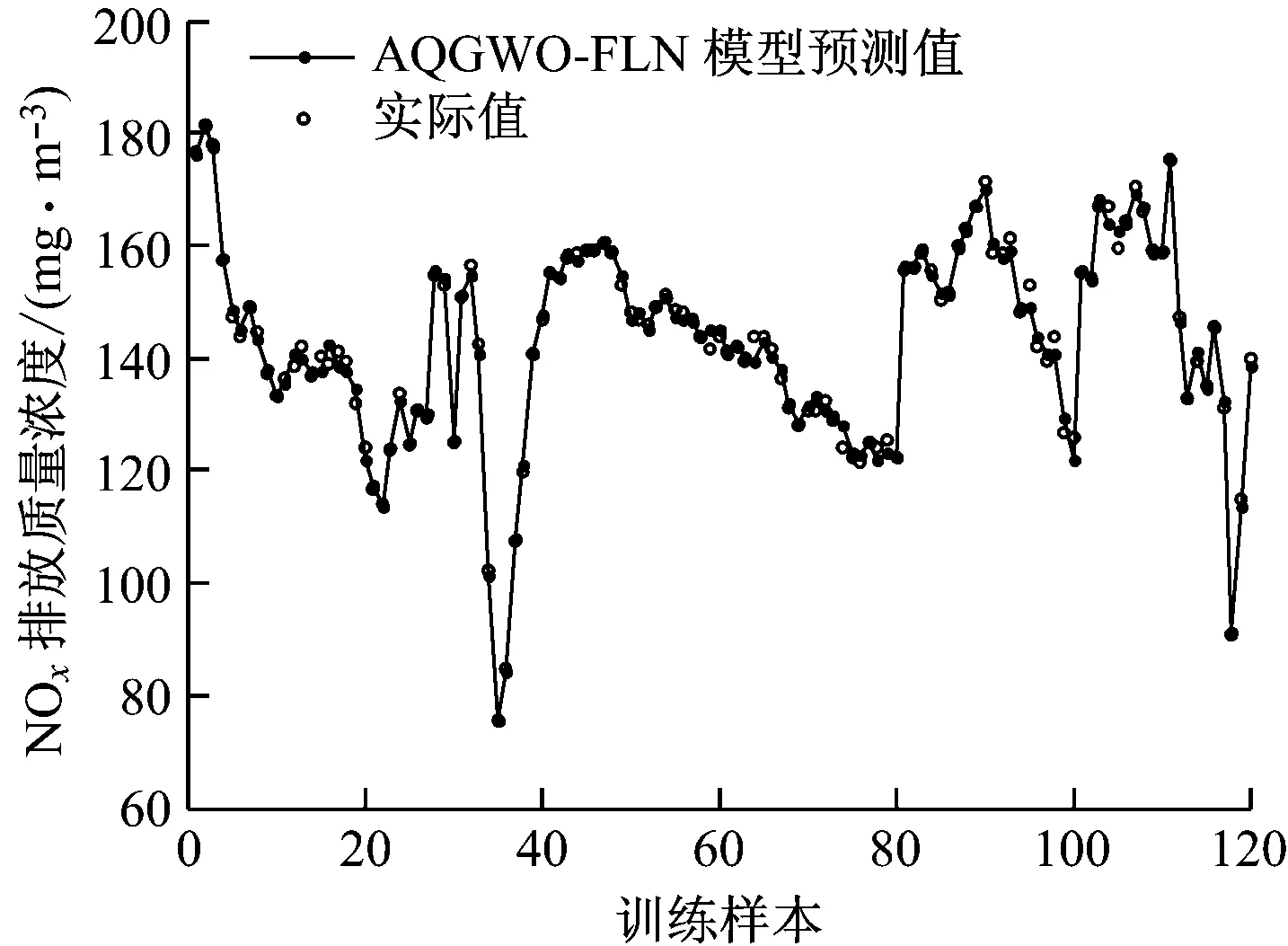
图5 训练样本预测值与实际值的对比

为了综合评价各模型预测值与实际值的准确度及预测效果，对均方根误差(RMSE)、平均绝对误差(MAE)、平均相对百分比误差(MAPE)和相关性系数(R-square) 这4个性能指标进行对比，同时采用FLN模型、DE-FLN模型、WOA-FLN模型、PSO-FLN模型和GWO-FLN模型对循环流化床锅炉的NOx排放质量浓度进行预测。各模型输入参数、输出参数和隐藏层节点个数的设置与前面一致，预测结果如表3和表4所示。

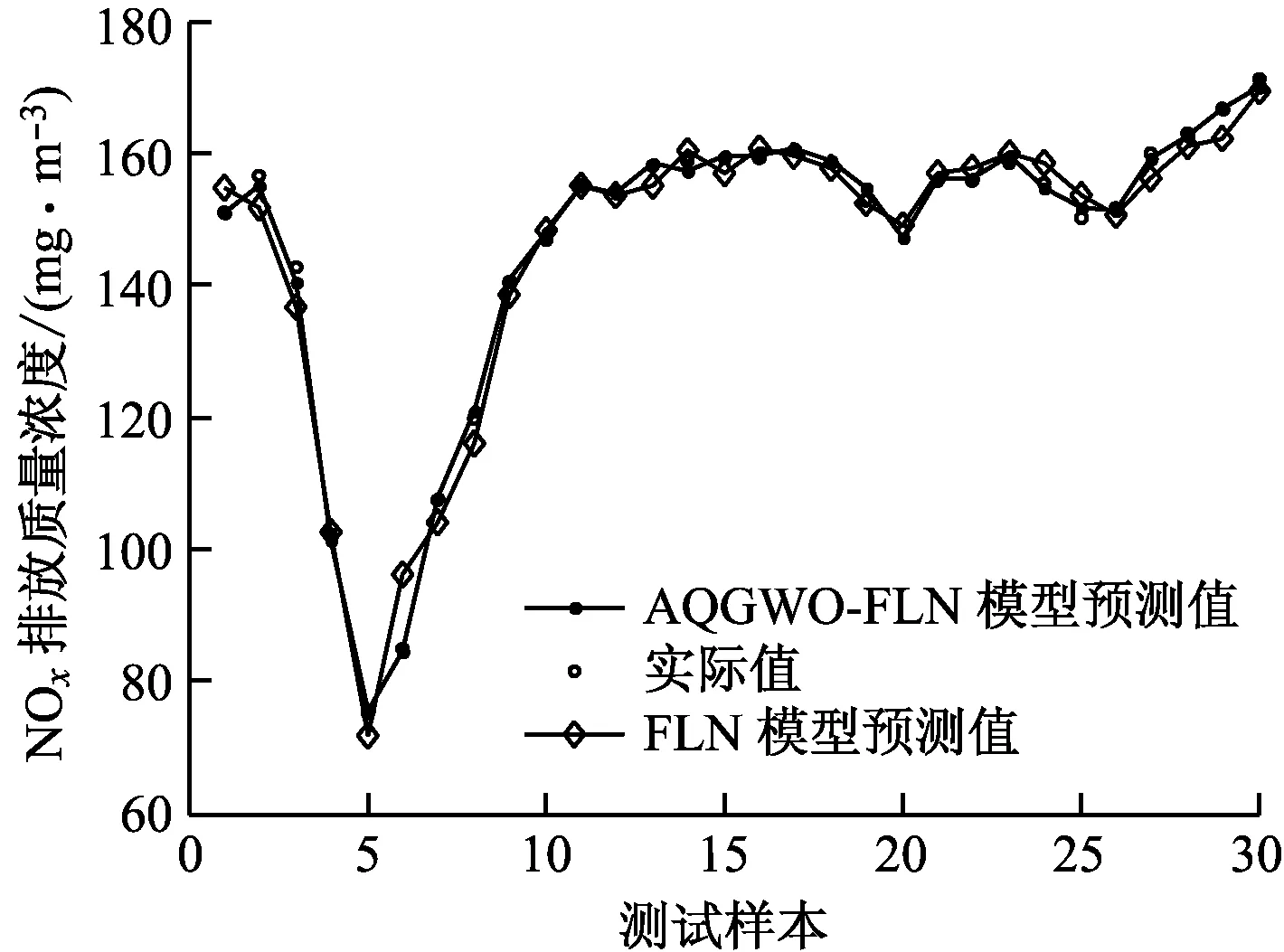
图6 测试样本预测值与实际值对比

由表3可知，对于训练样本，AQGWO-FLN的RMSE为1.518 2，MAE为1.155 8，MAPE为9.281 7×10-7，R-square为0.996 4，这4项指标均优于其他5种模型。因此，对于训练样本而言，AQGWO-FLN模型的预测能力和拟合精度均优于其他5种模型。

表3 训练样本的准确度对比

表4 测试样本的准确度对比

由表4可以看出，对于测试样本，AQGWO -FLN模型的RMSE为0.914 0，MAE为0.750 5，MAPE为7.593 6×10-7，R-square为0.999 2，这4项指标均优于其他5种模型，尤其MAPE模型比其他5种模型小2个数量级。因此，对于测试样本而言，AQGWO-FLN模型的泛化能力和模型预测精度均优于其他5种模型。结合表3和表4可知，虽然其他5种模型也能对训练样本进行很好地预测，但对测试样本的预测效果均没有AQGWO-FLN模型好。

各模型对测试样本的预测误差如图7所示。与其他5种模型相比，AQGWO-FLN模型预测NOx排放质量浓度的误差曲线较平稳，波动较小，最大误差也比其他模型小，这说明AQGWO -FLN模型的预测结果更准确。

图7 测试样本的预测误差对比

5 结 论

(1)采用量子位Bloch坐标编码初始化群体位置，迭代后期增加了变异算子和惯性权重，对原始灰狼算法进行改进。为了验证AQGWO的性能，采用8个经典的测试集函数对该算法进行了性能测试，并与基本GWO、WOA、DE、PSO进行了比较。结果表明，AQGWO模型收敛速度更快，收敛精度也更高。

(2)以某火电厂300 MW循环流化床锅炉为研究对象，利用改进的AQGWO-FLN模型建立了循环流化床锅炉NOx排放特性预测模型，利用得到的预测结果与FLN、PSO-FLN、DE-FLN、WOA-FLN模型和GWO-FLN模型的预测结果进行比较。结果表明，AQGWO-FLN模型可以更准确有效地预测NOx排放质量浓度，其预测精度、泛化能力均强于其他5种算法，为电站锅炉预测NOx排放提供了一种新的高效方法。

参考文献：

[1] 刘志强, 刘青, 蒋文斌, 等. 循环流化床锅炉SO2和NOx排放的影响规律研究[J].锅炉技术, 2013, 44(3): 23-27.

LIU Zhiqiang, LIU Qing, JIANG Wenbin, et al. The effect of the emission in circulating fluidized bed boilers[J].BoilerTechnology, 2013, 44(3): 23-27.

[2] 欧阳子区, 朱建国, 吕清刚. 无烟煤粉经循环流化床预热后燃烧特性及NOx排放特性实验研究[J].中国电机工程学报, 2014, 34(11): 1748-1754.

OUYANG Ziqu, ZHU Jianguo, LÜ Qinggang. Experimental study on combustion and NOxemission of pulverized anthracite coal preheated by a circulating fluidized bed[J].ProceedingsoftheCSEE, 2014, 34(11): 1748-1754.

[3] 牛培峰, 麻红波, 李国强, 等. 基于支持向量机和果蝇优化算法的循环流化床锅炉NOx排放特性研究[J].动力工程学报, 2013, 33(4): 267-271.

NIU Peifeng, MA Hongbo, LI Guoqiang, et al. Study on NOxemission from CFB boilers based on support vector machine and fruit fly optimization algorithm[J].JournalofChineseSocietyofPowerEngineering, 2013, 33(4): 267-271.

[4] 李霞, 牛培峰, 马云鹏, 等. 基于改良的鸡群优化算法优化锅炉NOx排放质量浓度[J].动力工程学报, 2017, 37(4): 293-300.

LI Xia, NIU Peifeng, MA Yunpeng, et al. NOxemission reduction of a boiler based on ameliorated chicken swarm optimization[J].JournalofPowerEngineering, 2017, 37(4): 293-300.

[5] 牛培峰, 陈科, 马云鹏, 等. 基于磷虾群算法的汽轮机热耗率建模应用[J].动力工程学报, 2016, 36(10): 781-787.

NIU Peifeng, CHEN Ke, MA Yunpeng, et al. Modelling of turbine heat rate based on krill herd algorithm and its application[J].JournalofChineseSocietyofPowerEngineering, 2016, 36(10): 781-787.

[6] 牛培峰, 赵振, 马云鹏, 等. 基于风驱动算法的锅炉NOx排放模型优化[J].动力工程学报, 2016, 36(9): 732-738.

NIU Peifeng, ZHAO Zhen, MA Yunpeng, et al. Model improvement for boiler NOxemission based on wind driven optimization algorithm[J].JournalofChineseSocietyofPowerEngineering, 2016, 36(9): 732-738.

[7] 牛培峰, 麻红波, 李国强, 等. 基于GSA-SVM的循环流化床锅炉NOx排放特性模型[J].计量学报, 2013, 34(6): 602-606.

NIU Peifeng, MA Hongbo, LI Guoqiang, et al. NOxemission characteristic model for circulating fluidized bed boilers based on GSA-SVM[J].ActaMetrologicaSinica, 2013, 34(6): 602-606.

[8] 梁志宏. 基于我国新大气污染排放标准下的燃煤锅炉高效低NOx协调优化系统研究及工程应用[J].中国电机工程学报, 2014, 34(S1): 122-129.

LIANG Zhihong. Study and engineering application of high efficiency and low NOxcoordinated optimization control system for coal-fired boilers based on new air pollutant emission standard[J].ProceedingsoftheCSEE, 2014, 34(S1): 122-129.

[9] 郭通, 兰巨龙, 李玉峰, 等. 基于量子自适应粒子群优化径向基函数神经网络的网络流量预测[J].电子与信息学报, 2013, 35(9): 2220-2226.

GUO Tong, LAN Julong, LI Yufeng, et al. Network traffic prediction with radial basis function neural network based on quantum adaptive particle swarm optimization[J].JournalofElectronics&InformationTechnology, 2013, 35(9): 2220-2226.

[10] KUMAR P, PANT M, SINGH V P. Modified mutation operators for differential evolution[C]//ProceedingsoftheInternationalConferenceonSoftComputingforProblemSolving. India: Springer, 2011.

[11] DING Shifeng, ZHAO Han, ZHANG Yanan, et al. Extreme learning machine: algorithm, theory and applications[J].ArtificialIntelligenceReview, 2015, 44(1): 103-115.

[12] LI Guoqiang, NIU Peifeng, DUAN Xiaolong, et al. Fast learning network: a novel artificial neural network with a fast learning speed[J].NeuralComputingandApplications, 2014, 24(7/8): 1683-1695.

[13] 李国强. 新型人工智能技术研究及其在锅炉燃烧优化中的应用[D]. 秦皇岛: 燕山大学, 2013.

[14] MIRJALILI S, MIRJALILI S M, LEWIS A. Grey wolf optimizer[J].AdvancesinEngineeringSoftware, 2014, 69: 46-61.

[15] MIRJALILI S, LEWIS A. The whale optimization algorithm[J].AdvancesinEngineeringSoftware, 2016, 95: 51-67.

[16] SYAFARUDDIN H, NARIMATSU H, MIYAUCHI H. Optimal energy utilization of photovoltaic systems using the non-binary genetic algorithm[J].EnergyTechnology&Policy, 2015, 2(1): 10-18.

[17] 易正俊, 何荣花, 侯坤. 量子位Bloch坐标的量子人工蜂群优化算法[J].计算机应用, 2012, 32(7): 1935-1938.

YI Zhengjun, HE Ronghua, HOU Kun. Quantum artificial bee colony optimization algorithm based on Bloch coordinates of quantum bit[J].JournalofComputerApplications, 2012, 32(7): 1935-1938.

[18] 傅彩芬, 谭文. 循环流化床锅炉燃烧系统的控制研究[J].热能动力工程, 2016, 31(2): 66-73.

FU Caifen, TAN Wen. The control of combustion system of circulating fluidized bed boiler[J].JournalofEngineeringforThermalEnergyandPower, 2016, 31(2): 66-73.

[19] 马宏明, 翟晓敏. 某电厂300 MW亚临界循环流化床锅炉钢结构设计介绍[J].锅炉制造, 2014(3): 16-17, 20.

MA Hongming, ZHAI Xiaomin. Design of steel structure for sub-critical 300 MW CFB boiler[J].BoilerManufacturing, 2014(3): 16-17, 20.

[20] 陈献春, 杨瑞来, 陈宇, 等. 300 MW循环流化床锅炉启动过程爆燃与结焦的预防及控制[J].电站系统工程, 2012(5): 24-26, 29.

CHEN Xianchun, YANG Ruilai, CHEN Yu, et al. Precaution and control of explosion and coking during startup in 300 MW CFB boiler[J].PowerSystemEngineering, 2012(5): 24-26, 29.