基于MATLAB风力机双馈感应电机的仿真研究

2018-04-24武桢

通信电源技术 2018年2期

武桢

（内蒙古工业大学电力学院，内蒙古呼和浩特 010080）

0 引言

20世纪70年代初期，第一次石油危机使人类的目光转向风能。当前，伴随着全球能源供应的持续紧张、生态环境的日益恶化，风能发电、光伏发电等可持续、无污染的发电形式正受到世界各国的日益青睐。文献[1-2]提出，在各种可再生能源中，风能具有取之不尽、用之不竭、环境友好、清洁无污染以及能量密度相对较大等优点。目前，风力发电己成为可再生能源发电形式中，技术最成熟、规模最大、商业化运行可行性最好、研究最多的发电形式。其中，双馈感应发电机是目前风力发电机的主要类型，得到了越来越广泛的应用。

1 风力发电机组控制结构

双馈风力发电机组由风力机、传动轴、齿轮箱、双馈感应发电机、双PWM变流器及其控制系统组成。叶轮是风力涡轮机捕获风能的重要装置，可以将风能转换成车轮轮毂上的机械扭矩；传动轴和变速箱的功能是将风力机的驱动作用转移到发电机，提高风速；双馈感应发电机与绕组异步电动机类似，功能都是将机械能转换成电能；机侧变流器和网络侧变流器是两个不同的电压源逆变器，分别通过背靠背的方式组成“双PWM变换器”；机侧变流器在矢量控制策略中，实现了对有功功率和无功功率的解耦；网络侧变换器的主要功能是在直流调节系统的控制下，保持恒定的电容电压和调节功率因数[3]。

2 双馈感应发电机数学模型

2.1 电压方程

三相定子绕组的电压平衡方程为：

三相转子绕组折算到定子侧后的电压方程为：

2.2 磁链方程

转子绕组的合成磁链由每个绕组的磁链和其他绕组组成。磁链方程方向基于磁链的方向[4]，故磁链方程式为：

由于各相绕组的对称性，可认为：

两相绕组之间只有互感，而互感可分为两类。

第一类互感为：

对于第二类定、转子间的互感，当两组绕组刚好在统一轴线上时，互感获得其最大值Lsr（此时的最大值又称为“互感系数）”。

将以上两类互感方程代入磁链方程中写成分块矩阵的形式，即：

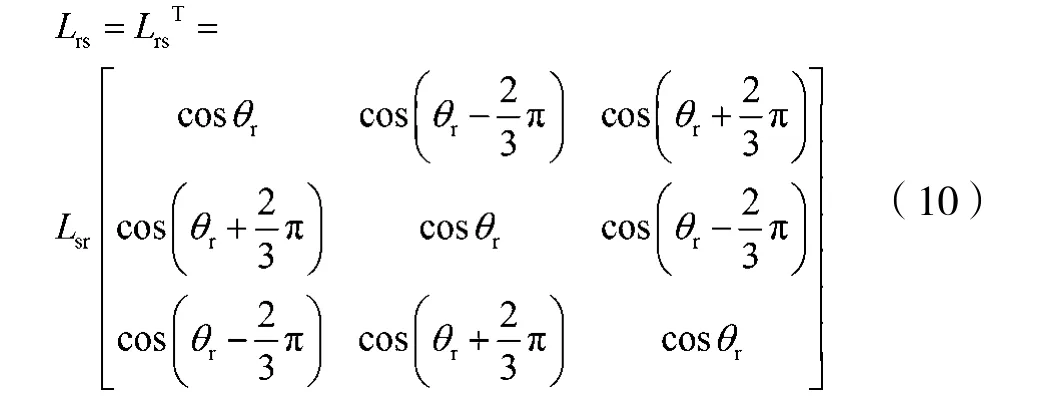
Lrs和Lsr两个分块矩阵互为转置，且与转角位置θr有关，其元素是可变参数，是系统非线性的来源。为了将变参数转换为常数参数，需要进行坐标变换，稍后将对此进行讨论。

2.3 转矩方程

转矩的计算方程为：

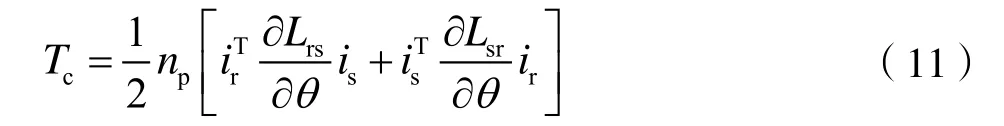
式中，np为极对数。

2.4 运动方程

为了方便，电机与转矩之间的摩擦力被忽略，力矩之间的平衡关系如下：

式中，Tm为原动机输入的机械转矩，Te为电磁转矩，J为系统转动惯量，np为电机极对数，w为电机的电动角速度。

根据机电能量转换原理，可以从磁场能量中求出电磁转矩方程：

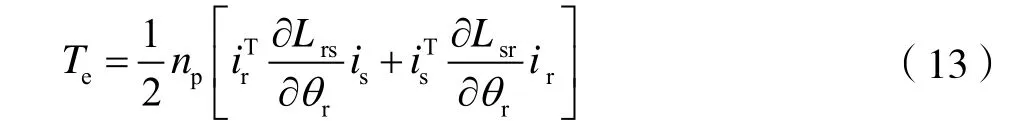
需要指出的是，式（13）是在磁路是线性的、磁场在空间上呈正弦分布的假设前提下得到的，但对固定转子的电流波形没有任何假设，是任意的。因此，电磁转矩式（13）有助于研究逆变器供电的三相转子绕组。

综上所述，完成了三相静止轴系统中交流励磁发电机的数学模型构建。

3 双馈感应发电机风力机

风轮从风中吸收的功率，可以用非线性公式表示：

风轮转矩为：

式中，λ=ωtR/v是叶尖速比；ωt是风轮转动角速度；v是风速；ρ是空气密度；R是风轮半径；β是桨距角（俯仰角）。风能利用系数 Cp(λ, β)和风能转矩系数 CT(λ, β)是λ和β的非线性表达式，二者的关系如下：

风能利用系数Cp(λ, β)可近似表示为：

Cp(λ, β)=(0.44-0.016 7β)

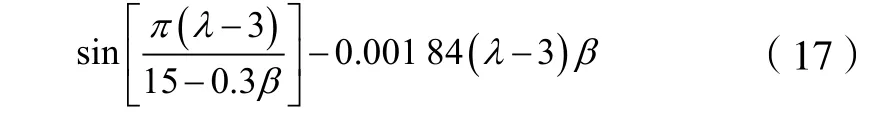
当λ为某一特定值λm时，Cp达到最大值。此时，风力输出最大机械功率，λm称为最佳尖速比。风能系数曲线如图1所示[5-7]。

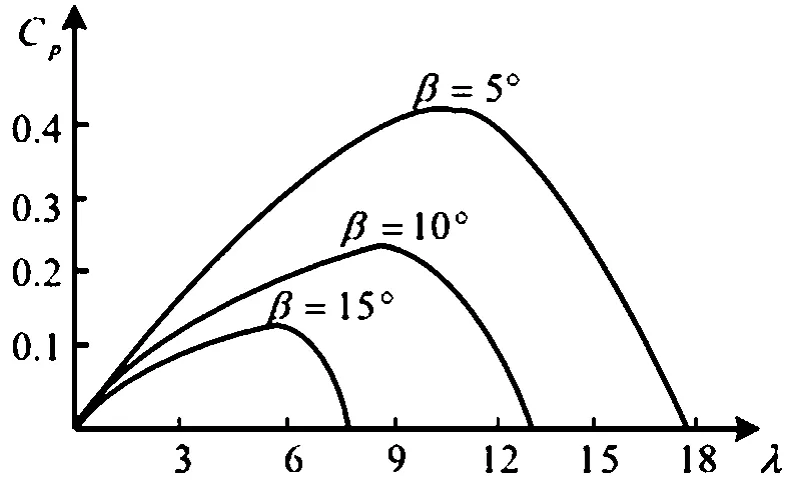
图1 风能系数曲线

对于变速变桨距风力发电机，在风速低于额定风速的情况下，采用主变速调节，即通过调节发电机转速获得最大转速比，从而获得最大风能转换功率；当风速大于额定风速时，变桨采用恒功率调节方式，即通过调节桨距角使发电机的输出功率基本等于额定功率[8]。变速变桨扭矩-转速关系曲线图，如图2所示。

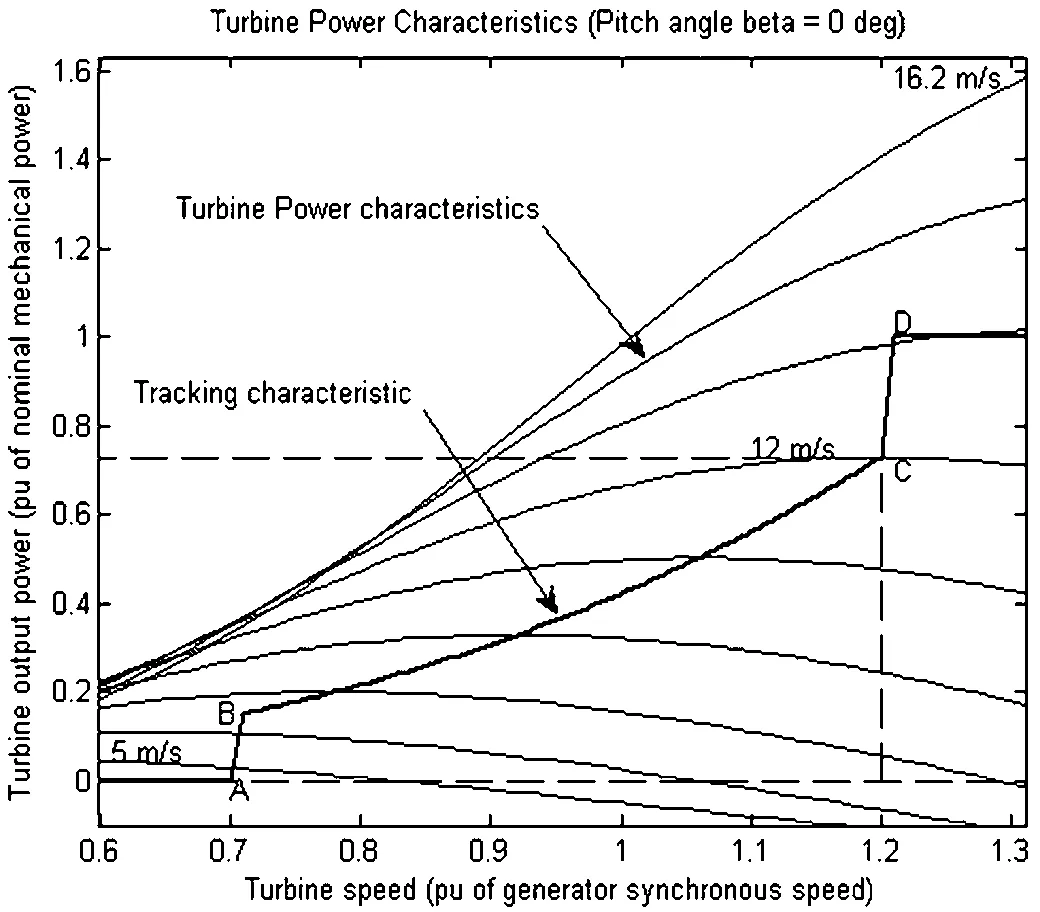
图2 变速变桨扭矩-转速关系曲线

曲线由A-B-C-D构成，分别为功率曲线和追踪功率曲线。当风速低于A时，风力发电机没有动作，输出功率为0；A-B段是风力发电机组的快速启动阶段，B-C段可视为风力涡轮机的变速控制在最大功率时的曲线轨道；C-D段不再增加风力机的转速，但转矩却在继续增大；风力发电机达到D点后，采用变桨距控制维持额定功率[9]。

4 仿真过程

9 MW风电场运行情况的仿真图，由6台1.5 MW风力机组成，如图3所示。

打开风力机双馈感应电机模块，分别设置发电机、变换器、风力机、控制系统四个组件的参数。在仿真工程中，风速输入信号为一阶跃信号，风速在时间为5 s时，由8 m/s阶跃到14 m/s。在变速变桨距风力机转矩—转速关系曲线中，C点风速设定为12 m/s，仿真时间为50 s。电网示波器主要显示电网电压经三个三相变压器变压后的输出电压信号、有功信号、无功信号、电机转速等信号；风力机示波器主要显示发电机有功信号、无功信号、转速、风速、桨叶桨距角等信号。

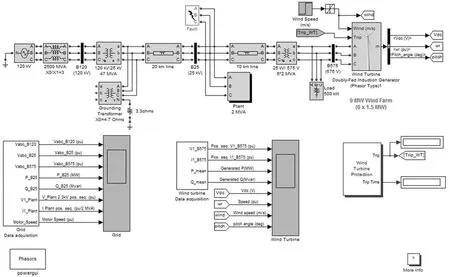
图3 9 MW风电场运行情况仿真图

电网示波器仿真结果，如图4所示。

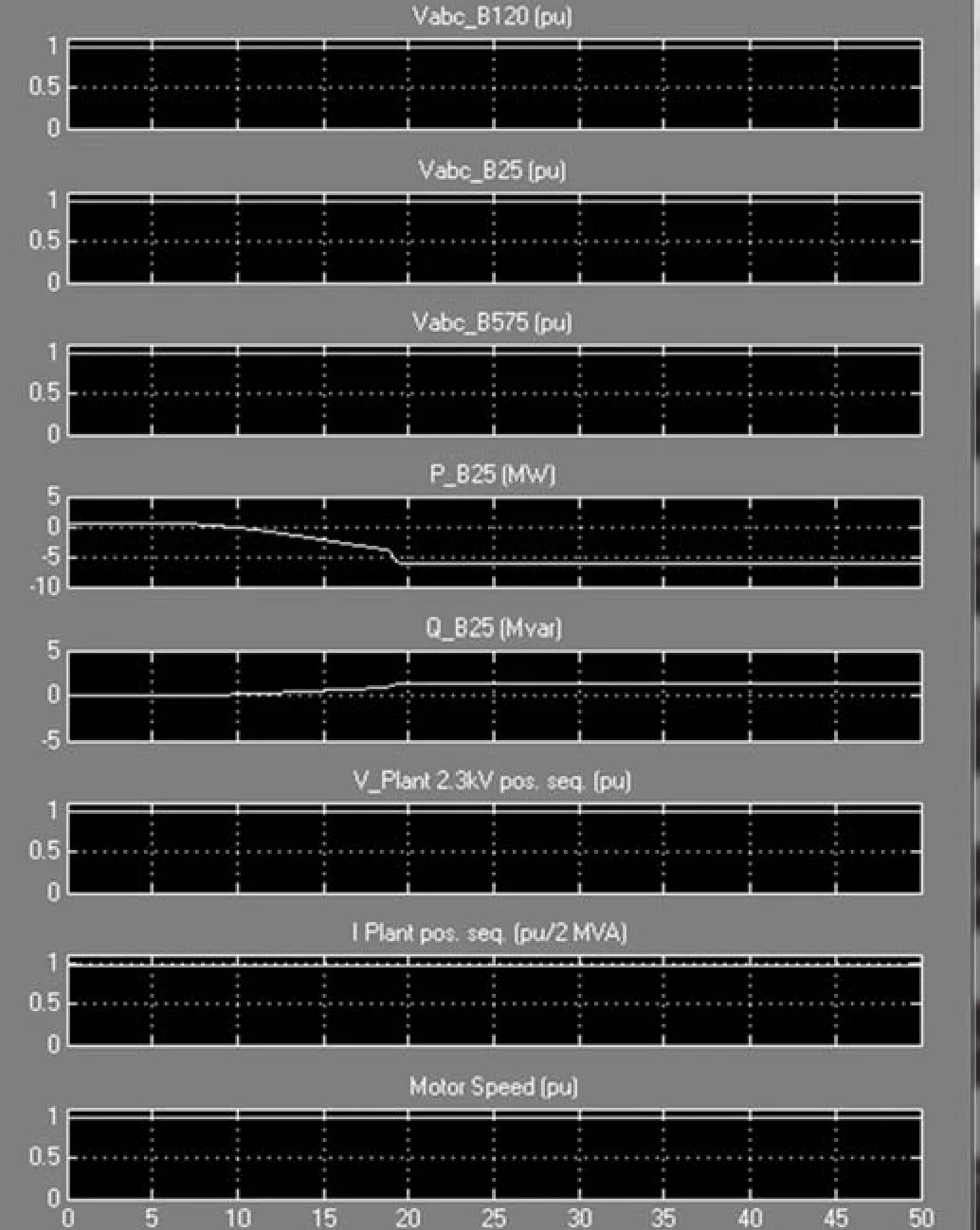
图4 电网示波器仿真结果

风力机示波器仿真结果，如图5所示。

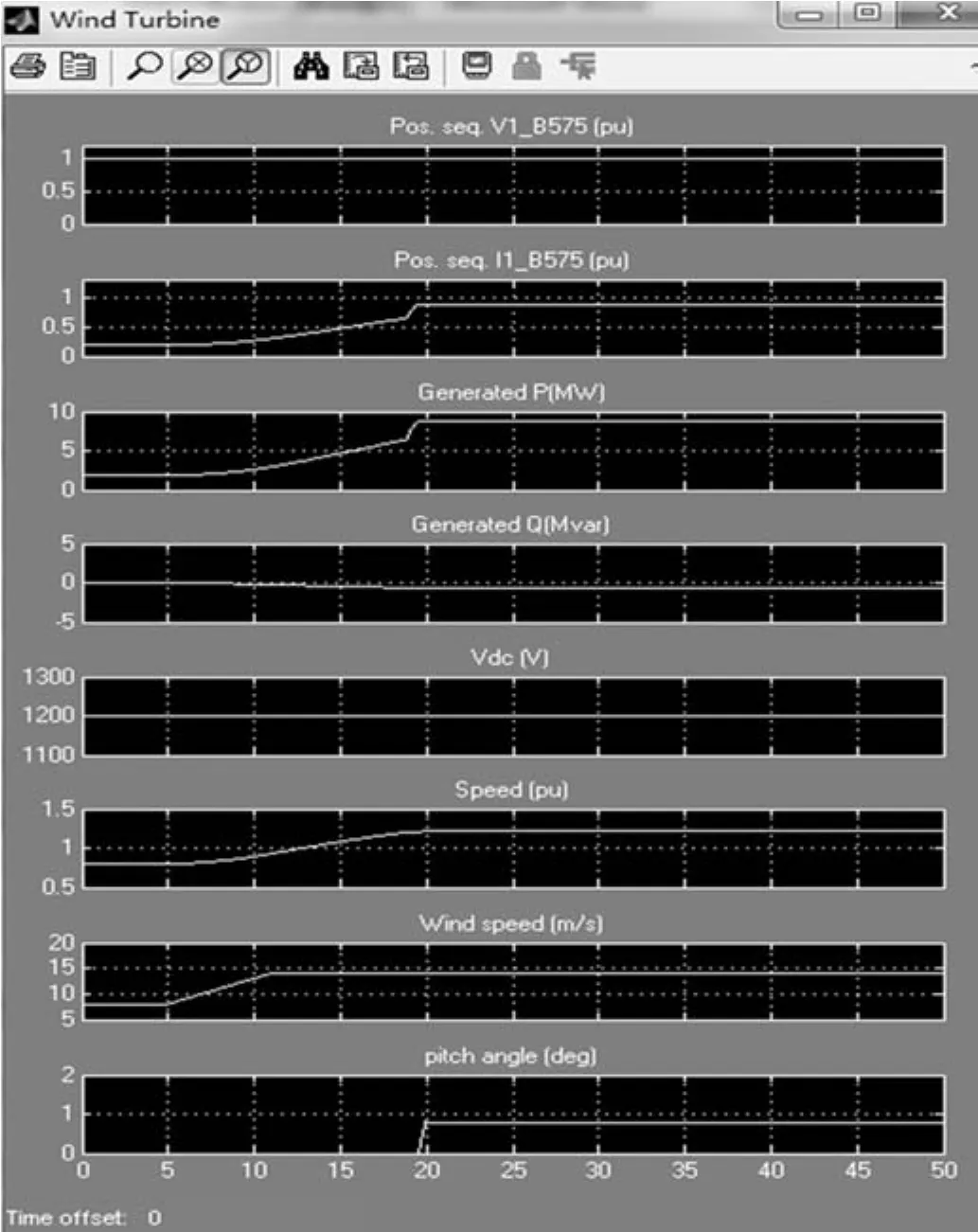
图5 风力机示波器仿真结果

5 仿真结果分析

风力机叶片吸收风能，风能带动齿轮箱工作产生机械能而产生机械功率，再带动发电机产生电能而产生电功率。5 s时增大风速，在5～10 s阶段，风速在额定风速以下，高于切入风速。此时，电机从电网吸收无功，使发电机转动。随后，有功功率开始增大，无功功率开始减小。当风速大于额定风速时，由于最大功率追踪特性、风力机的桨距角和仰角变化等因素，使得20 s时发电机达到额定转速，从而向电网发出一定量的无功。此时，有功达到额定值，无功也达到额定值，并都保持不变。