基于加权K-means聚类与路网无向图的地图分割算法

肖尚华，胡灿林

（四川大学计算机学院，成都 610065）

0 引言

依托高速增长的交通大数据体量与运算能力，智能交通与智慧城市已成为人工智能浪潮的一个重要组成部分。其应用包括OD推算，通勤时间预测及城市区域分割等多个方面。其中区域分割可通过将城市地图划分，达到简化并抽象城市交通网络的作用，并可作为其他某些应用的基础。

目前地图数据主要以向量化的路网无向图的方式对城市地图信息进行存储，其代表如GeoJson格式、Shapefiles文件等。以GeoJson文件为例，城市的地理信息主要以带属性的线段集合方式存储。每个线段由有序的经纬度坐标轴组成。每个经纬度线段集合可具有多个属性值，可携带该折线的类型（如高速公路、河流、铁路），名称等信息。而传统的地图分割算法均以像素化而非向量化的地图数据为基础。

传统的基于图像地图的分割中，普遍通过对像素点进行聚类进行实现[1-2]。数字图像的像素点由0到255的灰度值进行表示，其像素点灰度值的差异可通过多种范数进行衡量。不同的聚类方法，如均值漂移（Mean Shift）或谱聚类（Spectrum Clustering），可通过这些范数衡量相邻像素点之间的差异，从而对图像的每个像素点聚进行聚类。通过聚类后将图像不同的区域划分为不同的类，从而分割出图像中的不同物体，前后景。但由于基于向量表达的城市地图数据仅将有意义的地理信息以离散向量进行存储，其直观上并没有覆盖全部地理空间，故无法使用传统方法对其进行分割。为解决此问题，本文提出一种基于通过对路网无向图进行德劳内三角化，对地图数据进行加权K-means聚类的地图分割算法。并通过代码实现及可视化验证了该算法的有效性。

1 相关工作

本文主要依赖的现有工作为德劳内三角化[3]（De⁃launay Triangulation）以及K-means聚类[4]（K-means Clustering）。对于给定的离散点集合，德劳内三角化可将该点集转换为一个连通图，使得该图由三个一组且相互不相交的三角形回路组成。在得到三角的过程中，德劳内三角通过最大化每个三角内的最小内角来避免过于狭窄的三角形，故其可以看做是一种最优化问题。K-means是数据科学、图像等领域应用最为广泛的算法之一。对于给定的离散点集合及范数，其将与聚类中心最接近的点加入聚类中心所属的集合，并迭代的更新聚类中心直到收敛。故其可以非监督地方式将离散数据进行自动分类。

2 算法实现

2.1 地图数据的德劳内三角化

为了将向量化的地图数据转化为可覆盖整个城市二维平面的数据，首先将其德劳内三角化。以成都市锦江区为例，假设传入的地理信息为道路、河流等线段类数据及锦江区边界的多边形数据。其数据通过以下形式存储：

坐标列表：

[[104.0454671,30.4769304],[104.0453439,30.476933],……[104.0430272,30.4769812],[104.0368152,30.4769258]]

属性键值对："highway":"secondary";"name":"锦江路一段"……"oneway":"yes"

要得到铺满且不重叠的锦江区的德劳内三角，首先需要将位于锦江区内的坐标点过滤出。对锦江区边界构建多边形路径后，通过W.Randolph Franklin提出的PNPoly算法对所有地理信息点判断其是否属于该多边形路径。得到所有属于该区域的点后将所有同一条线路内两个相邻的点构成的线段依据其所属道路的属性赋予相应的权重，存储为权重字典。具体方法将在后文叙述。得到范围内的点后，将范围内的点加入边界点列表，形成一个完整的点集合。对该集合进行德劳内三角化，得到一个铺满且无重叠的三角集合，三角集合在地图上形成一个凸多边形。其中每个三角形以三个顶点的经纬度进行表示。

形成初步的三角集合后，需要将位于边界外的三角过滤。每个三角形设置一个标志位：对每条边，若该边的中点在边界内或该边属于边界集合，则标志位加1。若该三角形最终标志位不为3，则将该三角形删除。过滤后则可形成可用于聚类与分割的最终的三角形集合。最终三角形集合效果如图1所示。

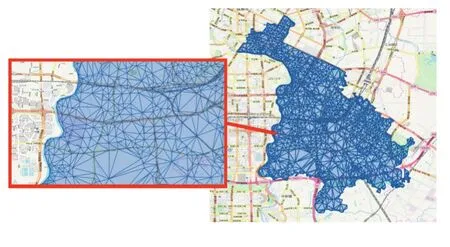
图1 德劳内三角化后的成都市锦江区地图

由图可见锦江区被切割为了互不重叠且铺满的三角形。

2.2 确定三角的中心

得到三角形集合后，为进行聚类，需要给每个三角形分配一个聚类时的代表中心。考虑到集合中存在大量的狭长三角形，而为实现更好的效果应该让长边相邻的三角形有限于短边相邻的三角形进行融合，故采用三角形中最长垂线的中点最为聚类时的代表中心。采用最长垂线中点为中心的效果与采用定点均值为中心的差异如图2所示。可以看到以最长垂线中点为中心时，狭长三角形显著地倾向于与长边相邻的距离更近。而以定点均值为中心时，这种倾向并不显著。

图2 左图为以最长垂线中点为中心，右图为以顶点均值为中心

2.3 三角中心的加权K-means聚类

对三角形进行加权聚类的目的是使聚类的边界能够最大程度地集中在地图数据中存在的道路、河流、铁路等现有线段上，以得到更有依据的划分与更好的视觉效果。此处加权K-means的核心思想是，对于分布在二维平面上由欧式距离衡量的待聚类的三角中心点，通过对欧氏距离加权的方式映射到一个新的距离空间上，再在这个空间上对三角中心点进行K-means聚类。故对于三角形的聚类可分为两步：新的距离空间映射，以及K-means聚类。

对于两个三角形中心，其连线与这两个三角形的公共边具有一定且唯一的交点。故要为每对三角中心点之间的距离分配的权重，可通过2.1中进行德劳内三角化前生成的权重字典获得。假设所有地图数据中原始的道路、河流线段集合构成一个地理线段集，则对任意公共边进行如下判断：若公共边不属于地理线段集的，则设权重为1；对于公共边属于地理线段集，且线段的属性为小型道路，如步道、小区道路，则设权重为1.5；若线段的属性为大型道路，如高速路、铁路，则设权重为3。分配权重后，由以下公式：

求得新的距离。其中i，j为三角形下标。

图3展示了对于一个聚类中心，进行54次迭代并得到一个由道路包围的区域的实现效果。可以看到，从第20次到第30次迭代时，虽然存在公共边为道路的两个三角形中心的原始欧氏距离更加接近的情况，但由于三角形中心已经被映射到了新的距离空间，故聚类中心仍然优先选择了处于道路同一方的其他三角进行了融合。由此可见，加权K-means可以使地图分割时更倾向于按照地图原有的地理信息作为边界进行分割与区域生成。

图3 对三角化后的进行加权K-means聚类的示意图

红框中1至4分别为迭代0次，迭代20次，迭代30次，迭代54次的效果图。

2.4 生成聚类边界

得到聚类区域的三角形集合后，需要解析出该类的边界。即以三角形所有边组成边集合，则删除所有处于区域内部的边，并将边界点有序排列，得到一个封闭多边形的顶点序列。由于所有区域的内部边一定为两个三角形的公共边，所以可通过删除所有重复的边得到边界的无序点集。而由于由多个三角形的边组成的区域一定为封闭边界，故每个边一定在两端与其他边具有相同端点。假设要从任意边出发，不断加入新的边以进行解析，则可通过迭代地寻找该边集合中与当前边界序列尾部具有相同端点的边，最终得到封闭的有序边界序列。

图4

3 算法实现及实验效果

在实验阶段，以基于Python的相关科学计算模块为基础实现了算法，其中通过Matplotlib模块实现了德劳内三角化，并通过Numpy和Scipy模块简化了向量运算。最终的输出为一个多边形列表，每个多边形由多个有序的经纬度对序列组成。形式如图4所示。

通过基于JavaScript的开源地图工具OpenLayers进行可视化后，最终区域划分效果如图5所示。可以看出，对于不同形状与大小的行政区域，地图基本上都基于道路、河流域铁路等具有实际意义的地理信息被划分为了不同的区域。并且在不同的切割数量上都可以达到较好的效果。

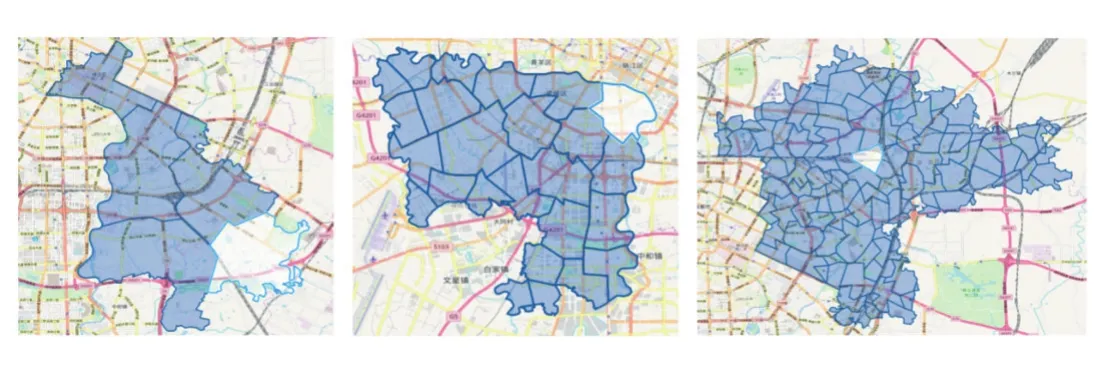
图5 对成都市下不同行政区划分为不同数量的区域

左为锦江区，划分为5个区域。中为武侯区，划分为25个区域。右为成华区，划分为100个区域。其中白色高亮区域为选中样式。

4 结语

本文针对目前流行的地图数据结构提出了一种自适应地图分割算法，并进行了代码实现及其可视化。该算法通过对向量化的地图数据进行德劳内三角化使数据能映射到整个地图边界所包含的二维空间，并通过加权K-means聚类的方式对三角进行融合，最终得到具有实际地理意义并符合视觉直觉的地图分割结果。

参考文献：

[1]吴信才,邓志勇,谢忠.彩色地图影像分割方法及其实现[J].上海：计算机工程,2003：29(1):176-177.

[2]郭玲,周献中.基于模糊最大熵原则的地图图像分割[J].成都：计算机应用,2002：22(11):18-19.

[3]Hartigan,J.A.;Wong,M.A.Algorithm AS 136:A K-Means Clustering Algorithm.Journal of the Royal Statistical Society.Series C(App-lied Statistics).1979：28(1):100-108

[4]Cignoni,P，C.Montani，R.Scopigno.DeWall:A Fast Divide and Conquer Delaunay Triangulation Algorithm in Ed.Computer-Aided Design.1998：30(5):333-341