一种多星测控下行多址干扰分析方法
2018-04-24韦欣荣徐军王万斌张宏杰
韦欣荣 徐军 王万斌 张宏杰
(北京空间飞行器总体设计部,北京 100094)
针对一箭多星发射过程中的多星测控问题,提出了一种适用于多星星地测控链路的下行码分多址干扰分析方法,构建了星箭联合体电磁仿真简化模型,并采用电磁仿真预测与多星干扰强度分析相结合的方法,评估受干扰信号的干信比上限,检验系统的兼容性。以构型为串联结构形式一箭双星发射的某中高度轨道双星为例,根据其主动段双星所处的构型布局和使用时机的复杂约束,分析评估单站同时接收双星下行码分多址扩频测控信号的多址干扰强度,并进行了双星主动段的在轨飞行试验。结果表明:该方法可有效分析多址干扰强度,满足工程实际应用需求。电磁仿真预测与多星干扰强度分析相结合的方法,为检验星地系统参数的兼容性,以及星箭飞行控制过程中地面站的使用策略提供了有效的支撑,可为类似的多目标工程应用提供参考。
多星测控;多址干扰;电磁仿真
随着一箭多星技术的发展,多星在运载火箭中的布局[1-2]也越来越复杂,同时在某些测控弧段内星地链路也会受到星箭联合体构型布局的影响,当多星采用同频码分多址测控体制时,地面站常使用单站同时对多星测控[3],此时多星下行测控信号均落在同一地面站天线波束范围和接收频带内,因而分析多星发射时,地面站对多星同时测控的电磁兼容性问题尤为重要。以往分析多星产生的多址干扰,往往仅从空间方位、信号功率等方面考虑,而关于多星复杂构型布局约束对多址干扰的影响涉及较少。本文描述了一种适用于多星测控的下行多址干扰分析方法,重点介绍了电磁仿真预测与多星干扰强度分析相结合的方法;并以构型为串联结构形式一箭双星发射的某中高度轨道双星为例,根据其主动段双星所处的构型布局和使用时机的复杂约束,采用该方法评估单站同时接收双星下行同频码分多址扩频测控信号而存在的多址干扰强度,评估受干扰信号的多址干扰干信比,即干扰与信号的比值,是否在多址干扰干信比上限内,以检验系统的兼容性。双星主动段在轨飞行试验的结果表明:该方法可有效地检验星地系统参数的兼容性,为星箭飞行控制过程中地面站的使用策略提供有效地支撑。
1 多星测控下行多址干扰分析方法及流程简述
多星测控下行多址干扰分析方法的流程如图1所示。
(1)首先根据火箭整流罩的构型布局,建立多星与火箭整流罩的星箭联合体简化模型,根据所建立的模型,仿真多个卫星的天线方向图增益;由于运载火箭是电大尺寸[4]物体,因此运载火箭和透波窗口需要用高频算法进行建模,例如MLFMM、UTD、PO、GP等算法[5-6]。模型包括整流罩、透波窗口、运载火箭、载荷、天线结构等信息。这种全结构模型虽然精确但是较为复杂,应用高频算法进行求解时需要花费大量的时间和内存,成为实际应用的瓶颈,因此需要对全结构模型进行简化。可将全结构模型简化为片段模型,片段模型的精度应满足工程应用需要。片段模型仅包含载荷表面、整流罩主面、透波窗口。
(2)对多星天线方向图增益仿真结果比对统计,得到地面站接收下行信号多址干扰干信比估计值。
(3)根据天线增益仿真结果以及实际应用中星地斜距、地面站发射等效全向辐射功率(EIRP)、卫星品质因数(G/T值)、卫星发射EIRP、地面站G/T值等参数,计算星地上、下行链路余量。
(4)以地面站接收载噪比和下行信号扩频码速率、数据速率等为输入参数,计算地面站能够承受下行信号多址干扰干信比的上限。
(5)将仿真的下行多址干扰干信比估计值与计算的多址干扰干信比上限比较,判断星地系统设计是否兼容,若兼容则可在轨使用,若不兼容则重新优化星地参数或者采取其他规避措施。
2 同频码分多址体制下多星发射主动段的测控下行链路干扰分析
2.1 建模与天线方向图仿真
某一箭双星采用长征-3A(CZ-3A)系列火箭发射,双星构型为整体吊外支撑的串联结构形式[7-8],双星在运载火箭整流罩中的位置为上下排列,运载火箭整流罩包括上星整流罩和下星整流罩,CZ-3A运载火箭整流罩与卫星的分离有4次,分别为:上星整流罩分离、上星与箭体分离、上星支架组合体与箭体分离、下星与箭体分离[7-8]。当双星在主动段测控时,所处的时机为上星整流罩分离而下星整流罩还未分离的场景下,此时上星的测控天线完全暴露在空间中,下星测控信号需要透过整流罩上开设的透波窗口与地面站建立连接,下星的下行信号较弱,易受到上星相对较强的下行信号的干扰。
双星均采用收发分开的遥控天线和遥测天线,采用电磁仿真软件FEKO,仿真算法为一致性几何绕射理论UTD算法,仿真时将实际模型结构简化为单体星箭结构模型,建立了整流罩分离后的上星和整流罩未分离的下星组合体仿真模型。由于UTD算法的限制条件为结构模型由多边形构成,多边形必须为无空洞的平面多边形,故通过平面多边形构建星箭联合体。仿真中所有金属表面均设定为理想导体,所有表面均设定为无厚度的薄面,透波窗口设定为无损自由空间,实际分析时将透波窗口的损耗加以考虑,按照3 dB计算。仿真采用辐射源等效方法,该辐射源为测控天线远场源。
仿真过程中可预见的误差如下:
(1)利用多边形模型进行圆柱体近似,将圆柱体近似为多边棱柱会引入一定的建模误差。
(2)建模仿真时忽略了星体表面载荷,仅将星体近似为光滑的立方体,立方体表面无任何物体,这样的近似忽略了星体表面载荷构形对天线方向图的影响,会引入一定的误差。
(3)利用远场辐射源近似,而天线与星体表面距离为近场,利用远场源近似会对近场耦合作用产生误差。
仿真模型和结果能反映遥控天线和遥测天线方向图趋势。
2.2 双星天线方向图增益及下星下行信号干信比仿真结果统计
上星整流罩分离而下星整流罩未分离时的仿真模型如图2所示,因为带整流罩的天线辐射区域是非对称且剧烈变化的,使用笛卡尔和极坐标天线方向图表示非对称的方向图并不是很方便,因此使用二维方向图表示,θ角和φ角的定义如图3所示,θ角为天线至空间某点P的矢量与+X轴的夹角,φ角为天线至空间某点P的矢量与+Y轴的夹角。图4为下星整流罩中遥测天线仿真方向图,可见在透波窗口范围内,遥测天线增益分布比较均匀,仅个别凹点小于-20 dBi。如图5~图8所示,可清晰地查询θ角和φ角所对应的天线方向图增益。由于系统设计时,透波窗口全区域的尺寸为25°≤θ≤44°,且63°≤φ≤76°,工程实际使用时留有一定的余量,主要使用区域约为28°≤θ≤41°,69°≤φ≤73°,根据仿真分析结果,表1中给出了上星整流罩分离后的遥控天线和遥测天线方向图增益值以及下星在整流罩内通过透波窗口的遥控天线和遥测天线方向图增益值。在主要使用区域,上星遥控天线、遥测天线增益值均大于等于1.5 dBi;下星遥控天线增益值大于等于-7.5 dBi,下星遥测天线增益值大于等于-14 dBi。
由于双星与地面站之间的斜距近似相等,空间损失相同,同一地面站接收双星发射信号功率差异主要是双星遥测天线在相同方向的增益差异。因此双星遥测天线在相同方向的增益差值即为地面站接收到的下星下行信号多址干扰干信比。所以根据图7所示的上星整流罩分离后遥测天线二维方向图增益仿真结果和图8所示的下星遥测天线通过透波窗口的二维方向图增益仿真结果计算,在主要使用区域,统计相同位置“上星遥测天线增益”超过“下星遥测天线增益”的情况,来评估地面站接收下星下行信号多址干扰干信比大小。
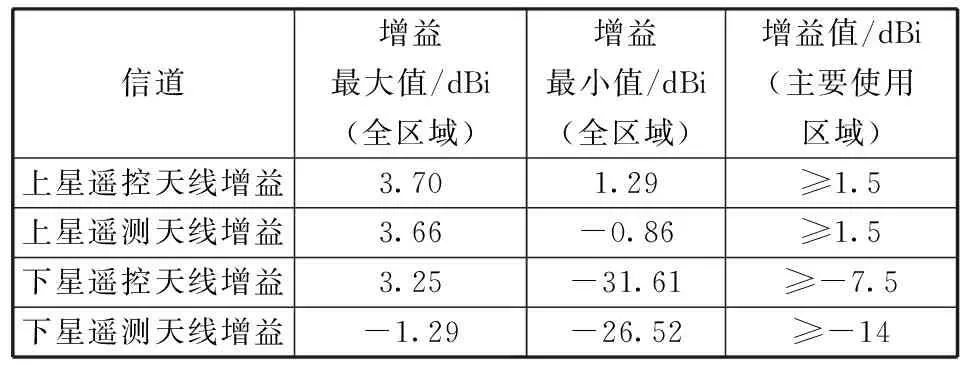
信道增益最大值/dBi(全区域)增益最小值/dBi(全区域)增益值/dBi(主要使用区域)上星遥控天线增益3.701.29≥1.5上星遥测天线增益3.66-0.86≥1.5下星遥控天线增益3.25-31.61≥-7.5下星遥测天线增益-1.29-26.52≥-14
由仿真结果统计可知,在相同位置,上星遥测天线增益超过下星遥测天线增益的范围为6~16.5 dB,超过15 dB的百分比为5.76%,超过16.5 dB的百分比为0%,即在94.24%的范围内地面站接收的下星下行信号干信比小于15 dB,100%的范围内地面站接收的下星下行信号干信比小于16.5 dB。具体数据见表2,L1表示上星遥测天线增益值;L2表示下星遥测天线增益值;(L1-L2)表示上星、下星的遥测天线增益差值。
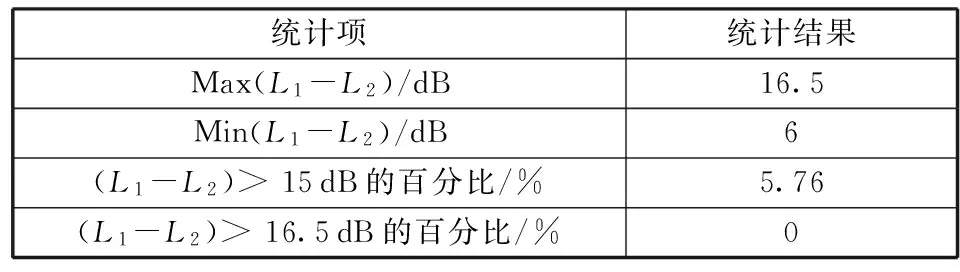
表2 双星遥测天线增益在主要使用区域的比较Table 2 Comparison of telemetry antenna gainof double satellites in the main using area
2.3 双星上下行信号链路计算
由于上星天线完全暴露在空间中,且主动段星地距离较近,所以上星的上下行链路余量充裕,这里主要分析下星的上下行信号链路余量。
下星上下行测控链路计算详见表3、表4,由于双星测控发生在主动段,星地距离较近,星地斜距按照200 km计算,地面站发射的EIRP值为65.0 dBW,卫星G/T值为-43.28 dB/K,卫星发射的EIRP值为-21.0 dBW,地面站G/T值为22.50 dB/K,天线增益按照表1中主要使用区域天线增益值最小值计算,在保留系统3 dB余量的基础上,下星对地面站的上行测控链路余量大于57.34 dB,下行测控链路余量大于32.79 dB,余量充裕,满足测控需求。
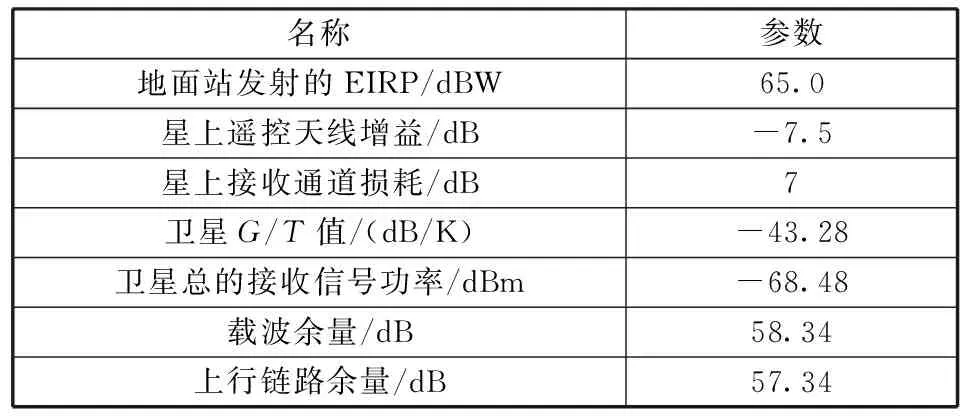
表3 下星上行测控链路计算结果Table 3 Uplink TT&C calculation results of down satellite
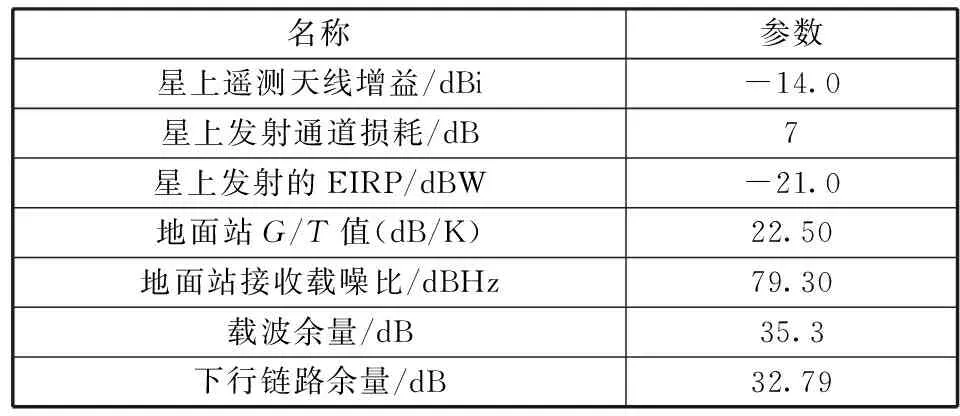
表4 下星下行测控链路计算结果Table 4 Downlink TT&C calculation resultsof down satellite
2.4 多星下行多址干扰干信比分析
对于扩频测控系统,其在轨应用时的下行干扰往往是多星之间同族码引起的多址干扰。假定有k颗卫星用各自不同的伪随机扩频地址码调制数据后发射,k颗卫星为同频码分多址信号,假设扩频前信号带宽为B1,扩频后带宽为B2,扩频伪码速率为Rc,数据速率为r,无信道编码,k颗卫星的下行信号落在同一个地面站的波束内。以地面站接收第一颗卫星发来的信号为例,设P1为希望接收的卫星发送来的信号功率,称之为有用信号,P2,P3,……,Pk为其他卫星发送来的信号,称之为多址干扰;此外还有敌方施放的恶意干扰功率J。
根据文献[9]所述,直接序列扩频系统在高斯白噪声干扰下的处理增益为
(1)
直接序列扩频系统在单频干扰下的处理增益为高斯白噪声下处理增益的一半,即
(2)
在干扰扩频伪码与有用信号扩频伪码的码率和码元宽度相同条件下,取多址干扰处理增益为
(3)
接收机的输入信干噪比为
(4)
式中:N0为噪声的谱密度,k为多星发射时的卫星总数,Pi为第i颗卫星发送的信号功率。假设没有恶意干扰,即J=0。经过解扩处理后,有用信号的带宽由B2缩减为B1,带宽为B2的白噪声、多址干扰,经过带宽为B1的窄带滤波器后,得到式(5)所示的输出信干噪比为[9]
(5)
保证系统正常工作条件下的输出信干噪比应大于(S/N)th,即
Ro≥(S/N)th
(6)
式中:(S/N)th为保证系统正常工作所需要的输出信噪比。
由式(5)和(6)得
(7)
由式(7)可得到多址干扰干信比的最大值为
(8)
式中:[]表示对[]内数值取10lg()后的dB值。假设为双星测控,下行遥测数据速率r=2000 bit/s,扩频伪码速率Rc=5.115 MHz,即k=2,B1=2 kHz,B2=5.115 MHz,于是由式(1),处理增益[Gp1]=10lg (5 115 000/2 000)=34.07 dB。
假设地面站下行遥测数据接收误码率为10-6,解调需要的比特信噪比为10.5 dB,考虑解调损失为3 dB,其他损失为1 dB,则保证系统正常工作所需要的输出信噪比[(S/N)th]=10.5+3+1=14.5 dB。
计算时,取主要使用区域内下星下行信号在地面站接收机输入端的载噪比最小值,由表4中下星下行链路计算得到,即C/N0=79.3 dBHz,C为载波功率,则仅考虑噪声时的下星下行信号输入信噪比的最小值[(S/N)n]=C/N0-10lgB2=79.3-10lg(5.115×106)=12.2 dB,该值对式(8)的计算结果可忽略不计。

2.5 综合数据分析
在轨主动段飞行过程中,下星应答机输入端的自动增益控制(AGC)电压为2.7 V~3.2 V,对应的接收端功率电平约为-70 dBm~-57 dBm,即下星上行链路余量大于55 dB;同时地面站接收的下星下行信号载噪比大于80 dBHz,下行链路余量大于30 dB。2.3节仿真计算的下星上下行链路余量与在轨飞行试验结果相吻合。
2.2节中统计得到94.24%的范围内地面站接收的下星下行信号干信比小于15 dB,100%的范围内地面站接收的下星下行信号干信比小于16.5 dB。与2.4节中所计算的地面站能够承受的下星下行信号多址干扰干信比的上限15.3 dB相近,系统兼容,可以满足使用要求,如表5所示。

表5 仿真分析与在轨试验结果比较Table 5 Comparison of simulation results andtesting results in-orbit
下星主动段在轨飞行过程中,在上星整流罩分离,下星整流罩未分离的弧段内,在多址干扰条件下,地面站下行信号锁定跟踪正常,遥测、遥控功能正常。
3 结束语
文章针对一箭多星发射过程中的多星测控问题,提出了一种适用于多星星地测控链路的下行码分多址干扰分析方法,以同频码分多址体制下多星发射主动段测控下行链路干扰分析为例,进行了仿真分析和在轨验证,结果表明:
(1)采用电磁仿真预测与多星干扰强度分析相结合的方法,以定性地评估受卫星复杂构型布局和使用时机约束的地面站下行多址干扰形势,检验星地系统参数设计的合理性和兼容性。
(2)所提出的电磁仿真简化模型可有效仿真复杂结构的电磁环境,仿真结果能反映天线方向图趋势,满足工程使用要求。
(3)对下星上下行测控链路余量、地面站接收的下星下行码分多址信号干扰分析预估结果,与在轨试验数据相近,满足工程使用要求,证明该方法可行。
本文的分析方法具有一定的普适性,对类似的多目标测控工程应用具有一定参考价值。
参考文献(References)
[1] 崔相臣.某大型卫星电磁兼容性设计与验证[D].上海:上海交通大学,2014:4-5
Cui Xiangchen. Design and validate of a large satellite elect romagnetic compatibility[D]. Shanghai: Shanghai Jiaotong University,2014:4-5 (in Chinese)
[2] 侯燕春,黄皓,姜铁华,等.某运载火箭舱内无线系统电磁兼容性仿真分析方法与应用[J].环境技术,2014,12(z):56-57
Hou Yanchun,Huang Hao,Jiang Tiehua,et al. Simulation technique and application of EMC of radio system in a carrier rocket chamber[J]. Environmental Technology, 2014,12(z): 56-57 (in Chinese)
[3] 吴斌,黄学祥,黄永宣.中低轨道卫星多星测控存在的问题及其改进措施[J].宇航学报,2003,11:629-630
Wu Bin,Huang Xuexiang,Huang Yongxuan. The existing limitation and corresponding improvements of LEO multi-satellite TTC[J].Journal of Astronautics, 2003,11:629-630 (in Chinese)
[4] 林昌禄,聂再平.天线工程手册[M].北京:电子工业出版社,2002
Lin Changlu, Nie Zaiping. Antenna engineering handbook[M].Beijing: Publishing House of Electronics Industry,2002 (in Chinese)
[5] Choong Seok Oh, Byung Chan Sun, Yong Kyu Park,et al. Payload fairing separation analysis using constraint force equation[C]//International Conference on Control, Automation and Systems. Korea: Institute of Control, Robotics and Systems,2010: 1134-1138
[6] Steven A Lane, Scott Kennedy, Robert Richard. Noise transmission studies of an advanced grid-stiffened composite fairing[J]. Journal of Spacecraft and Rockets, 2007, 44(5): 1131-1139
[7] 王向阳.美国运载火箭多星发射和搭载发射技术[J].导弹与航天运载技术,1994(5):1-11
Wang Xiangyang. United States launch vehicle in multiple payload mission and in carrying payload mission technology[J]. Missiles and Space Vehicles,1994(5):1-11 (in Chinese)
[8] 张涛,吴义田,胡炜,等. CZ-3A系列结构总体双星发射技术研制现状与展望[J].导弹与航天运载技术,2014(4):1-4
Zhang Tao, Wu Yitian, Hu Wei,et al. Current situation and prospect of dual launch technologies of the LM-3A series launch vehicle’s structure overall design[J]. Missiles and Space Vehicles,2014(4):1-4 (in Chinese)
[9] 夏利利,吴有杏,薛军,等.扩频测控系统干扰容限的再分析[J].遥测遥控,2012,9(5): 17-18
Xia Lili, Wu Youxing, Xue Jun, et al. Further analysis of jamming marjin for spread spectrum TT&C systems[J].Journal of Telemetry, Tracking and Command,2012,9(5): 17-18 (in Chinese)
