简单流体系统的建模与仿真

孙 建，张 奇

(中海油能源发展股份有限公司采油服务分公司，天津 300451)

1 单个水槽系统的动态模型

考虑如图1所示的单个水槽模型，其水槽底的液体流出的速度是槽内的液压决定的。各部分的含义为:A—蓄水槽的表面区域;V—水槽的容积;Ae—水槽出口处的联通部分;P1—槽底的液压.液体的输出压强为Pa,输出液体的速率作为系统的输入.系统的状态变量包括槽内液体的高度,其系统输出为液体流出的速率We.根据系统的物质平衡,可得到:

图1 单水槽系统示意图

假设蓄水槽的四周壁是垂直的,槽内液体的质量是液体的密度诚意液体的体积,有

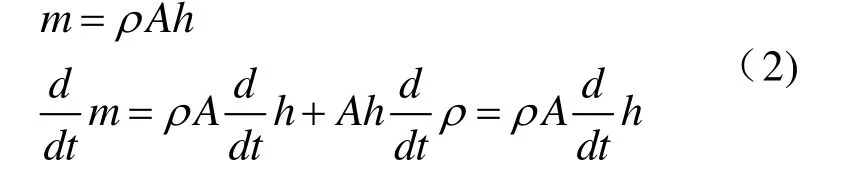
输出液体的质量可以写成输出速率的函数

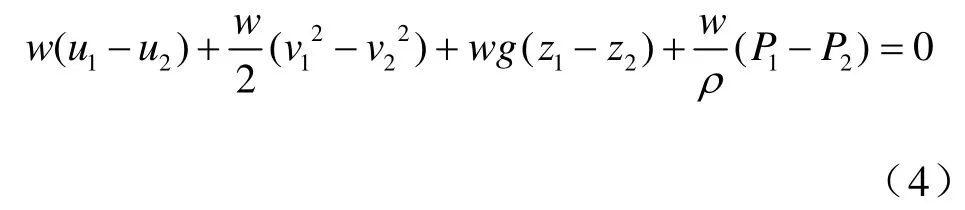
假设整个系统不存在能量或物质的滞留,并且忽略内部能量的变化,则根据能量守恒原理可以得到(5)：

综合上面的方程得出

显然该系统的状态方程是一阶非线性的,槽内液体质量的瞬时变化等于输入的液体速率渐趋输出的速率,槽内的液体质量和输出液体的速率都视作t时刻液体高度的函数.

以上得出的方程显然与显示生活中的系统差别较大,可以逐步进行改进以得到更精确的模型.定义液体的阻力作用,它的作用与电路中电阻的作用类似:

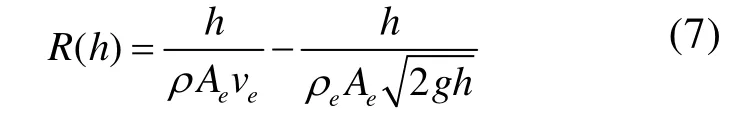
与此类似,还可以定义该系统的电容效应,它反映了水槽存储液体容量的变化.

将(7)和(8)代入式(6),得到

该非线性系统也可以线性化并写成标准的状态方程形式.定义系统的参考位置：

系统方程(1-6)可以写成

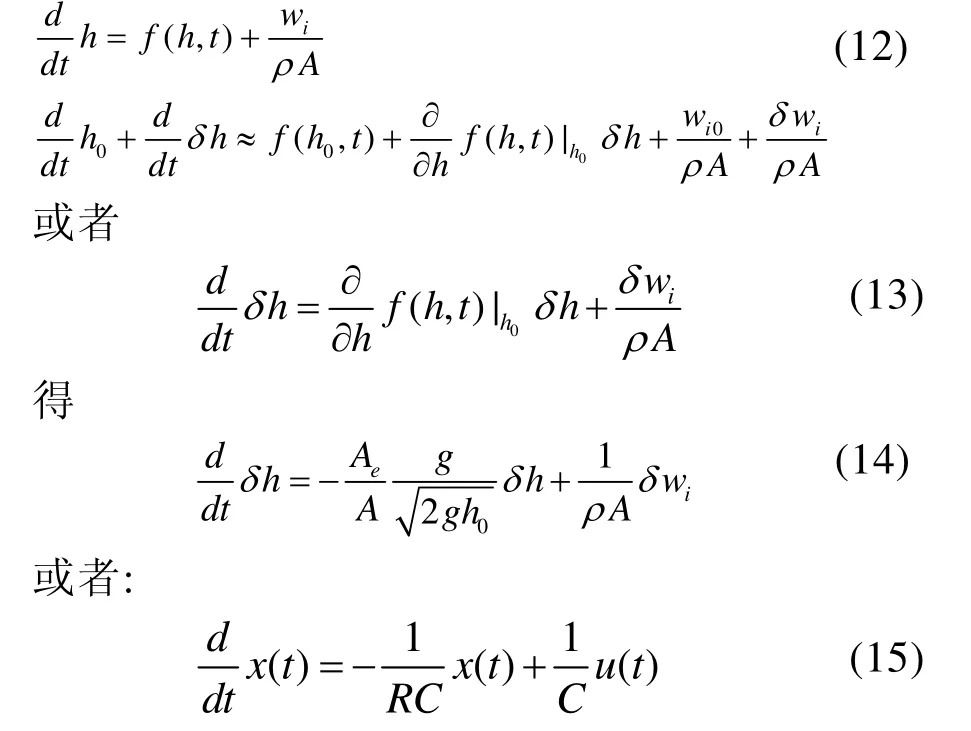
式(15)即为系统的线性化模型[1]。为了比较非线性系统线性化前后的系统响应.定义系统参数:

系统参考位置的系统参数为：

依据上述参数可以对系统进行仿真，图2显示的分别是Wi分别改变10%和50%时非线性系统和线性化模型的阶跃响应曲线。图3、图4给出了该系统线性化模型的频域仿真结果[2]。

图2 单水槽时域特性

2 双槽水槽系统的模型建立

在实际应用中经常存在互相联通的多个蓄水槽系统,这使得系统呈现出更高阶动态系统的特性.下面以双联通的蓄水槽系统为对象,研究二阶系统的动态行为。

图3 系统线性化模型的BODE图

图4 其它频域特性（Nyquist曲线和Nichols图）

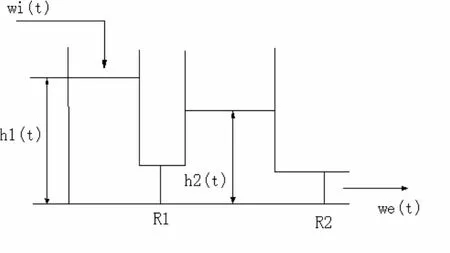
图5 双水槽系统示意图

按照第1节对单个水槽的分析,可以确定1号和2号蓄水槽的液体输出流量分别为[3]

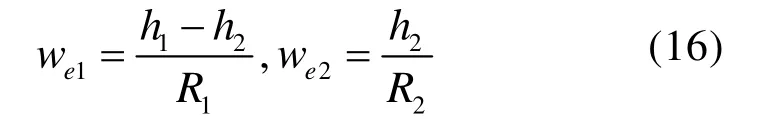
从而得到两个蓄水槽的平衡方程为：

将上面的结果写成标准的状态方程形式,并且将液体输出流速作为系统输出,则：

上述方程中的h1,h2 和 wi实际上是相对于参考位置的偏移量(即h1=δh1等)。为了创建系统的simulink方框图,只要针对状态方程中每个SISO子系统绘制它的框图,如下所示,然后将它们连接起来即可。

图6 各个子系统的框图

仿真框图如下所示：

图7 整个系统的框图结构

整个系统的传递函数可以通过矩阵运算或相关模块框图计算得到：

上式代入式(19),得到：

整理后得到整个系统的传递函数为：

图8和图9为该系统的脉冲和阶跃响应的部分仿真结果,程序对双水槽系统的 两种不通情况进行了仿真.一种是针对系统参考位置的动态行为进行了仿真.一种是将1号水槽的容积增加了1倍,这将导致系统时间常数的增加。

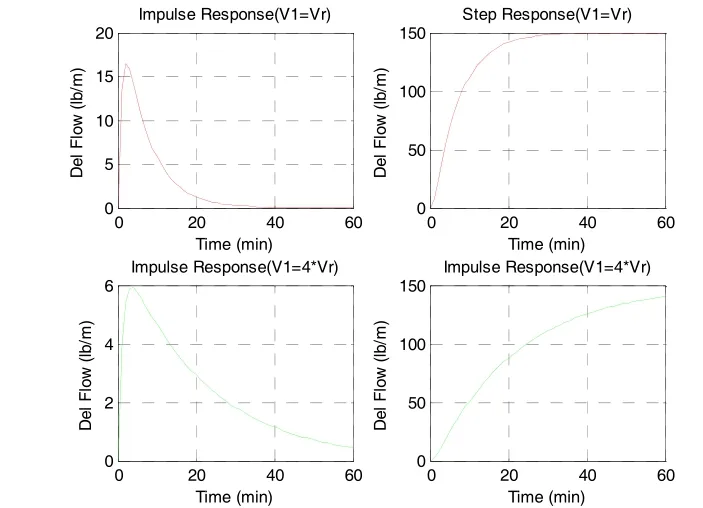
图8 双水槽系统的时域响应

3 结束语

在以上两个系统的建模与仿真中，分别建立了非线性和线性模型，仿真时对系统参数做了修改，以求得到反映系统特性的信息，在仿真结果中比较明显反映出了这些差别，可见对于此类基础的模型建立与仿真对于加深对系统的认识具有很大意义。

图9 双水槽系统的Bode图

参考文献：

[1] 郑阿奇.MATLAB实用教程[M].北京：电子工业出版社,2011

[2] 赵文峰.MATLAB控制系统设计与仿真[M].西安：西安电子科技大学出版社,2002

[3] 金以慧.过程控制[M].北京：清华大学出版社,2005.