巧妙转化，提高效率——把“和积互化”公式回归高考

胡宸溪

（宝鸡中学 陕西宝鸡 721013）

对于绝大多数高考考生来说，数学科目时间紧，任务重。而对于优生来说，既要有速度，给压轴题足够的思考时间，也不能忽视了质量。如何在有限的考试时间里更合理地分配时间，有效地提高做题效率自然就成为了大家关注的问题。本文将介绍提效 “法宝”之一——三角函数 “和积互化”公式的巧妙应用。

“和积互化” 公式包括两方面内容，即“和差化积”公式组和“积化和差”公式组，其基本内容如下：

可以看到，“和积互化”公式架起了三角函数的乘积与加和的“直通桥”，在一些三角函数类题目中，考生不必利用基本公式展开计算，从而提高了运算速度，在考场争得宝贵时间。

下面谨以几道高考题让读者体会用“和积互化”公式解决此类问题的优势。

例1.（2012.天津）已知函数

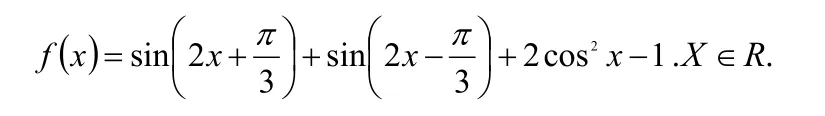
（1）求函数f(x)的最小正周期.

（2）求函数f(x)在上的最大值和最小值.

常规解法：

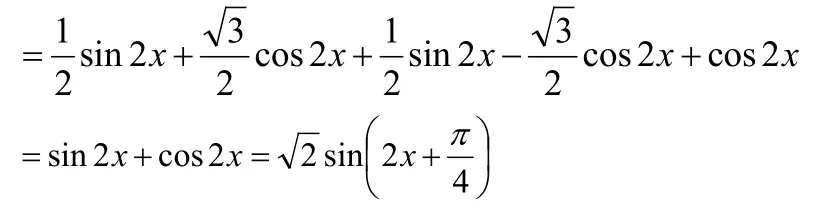
（先用和差角基本公式展开，然后用和差角公式化成标准形式）

∴最小正周期为：π.

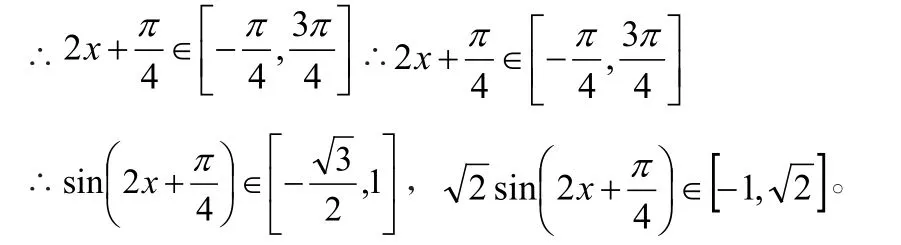
“和差化积”解法：

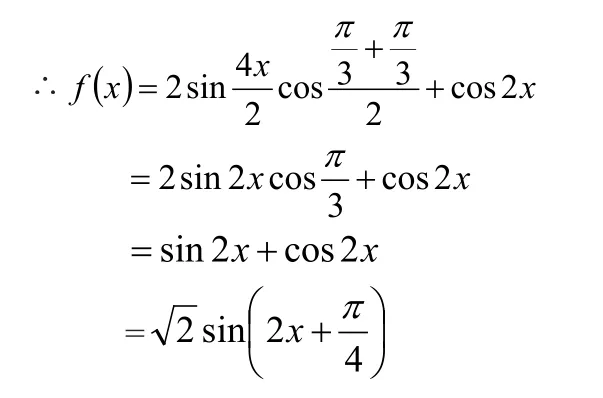
（步骤精简，转化快速，同时也减少了犯错误的机会）。

例2.4cos5 00-tan4 00等于（ ）

常规解法：

此方法对考生的“三角函数感”有一定的要求，不能深刻地理解特殊角三角函数转化方法的考生，解此题有一定难度，如果能借助“和积互化”公式，解决问题的过程会变得行云流水

“和差化积”法：

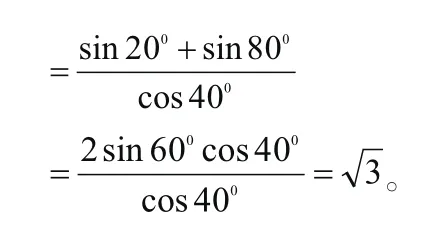
“积化和差”法：

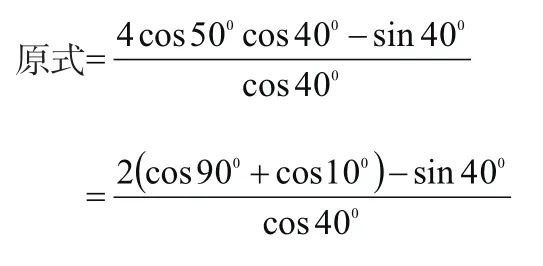
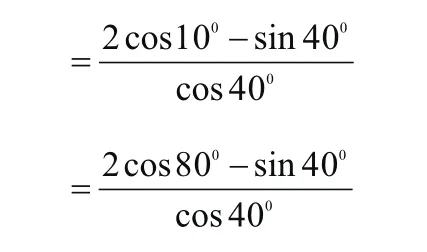
通过以上例题意在让读者体会到 “和积互化”公式的巧妙性，它让考生直达题旨，既精简过程，提高速度，又可减少思维量，增加流畅度。高考考场上，细节定成败，分秒必争取，若拙文能够激发读者对于 “和积互化”公式的关注与兴趣，并激励起更多 “和积互化”公式的探究与尝试，笔者不胜感激。