完全服务和非对称门限服务两级轮询系统特性分析

杨志军 苏杨 丁洪伟

轮询服务系统代表了一类调度控制的模型,因为其拥有较好的公平性,所以它不仅可以让有限的资源得到有效的分配,而且可以让资源得到共享[1−2].按服务方式的不同,轮询服务系统可以分为门限、完全以及限定三类[3−4].在三种基本的轮询服务模型的基础上,可以构成多种混合式区分优先级的轮询服务.文献[4]利用延迟周期的概念,给出了各类型客户等待时间的精确LST(Laplace steltjes transform)表达式和表示方法.此外,证明了优先级较小的平均服务时间的客户可以缩短平均响应时间,尤其是在繁忙的交通当中.文献[5]提出了一种基于闸门式多级门限服务的两级优先级轮询系统,该轮询系统满足了周期性系统服务资源分配过程中业务多样性和弹性服务的发展需求,使得轮询控制策略应用方面更为广泛.文献[6]提出了一种新型的两级优先级轮询系统,既保证了队列优先级的需求,又避免了空闲查询时造成的时间延迟,达到了提高系统的利用率,减少时延的效果.文献[7]分析了队列中在不区分优先级和区分优先级的情况下,对每一个队列提供门限服务或者是完全服务.并根据于此建立数学模型,然后对此模型的联合队列长度、循环周期、边际队列长度和时延等性能特点进行了解析,验证了区分优先级所带来的显著成效.对轮询系统区分优先级主要目的,是旨在让轮询系统的性能得到显著的提升.在优先级轮询的应用方面,它可以用于蓝牙技术和IEEE 802.11无线局域网协议的研究或是在Web服务器的路由器和I/O子系统中的调度策略.例如,保证服务质量(Quality of service,QoS)是无线LAN协议中非常重要的问题,虽然延迟对响应或数据传输不会产生重大影响,如网页浏览或电子邮件流量,但是视频传输和无线局域网语音(VoWLAN)对延迟或数据丢失却是非常的敏感.所以,802.11e则引入了不同的优先级来区分为类型之间的数据提高流媒体业务的服务质量.优先级轮询模型也可以用来研究流量,比如在交通路口,交通流同时面对绿灯时的情况.由此看出,对轮询系统进行优先级区分的研究有着重大的意义.

本文也是对区分优先级的两级轮询服务进行了研究,所不同的是,本文选择了一种对称性轮询服务与非对称性轮询服务相结合的混合式服务模型.为了更好地适应实际应用的需求,非对称的轮询服务分析一直是研究的热点,但实质性突破相对较难.由于在实际应用中,经常会有不同类信息或不同类站点,相应要求在同一种服务策略下,系统设置的参数需要满足不同类站点自身所需的要求,这就需要非对称的服务策略.由于轮询系统中各队列之间是相互联系的,而且系统的概率分布特性非常复杂,所以在对多队列的非对称轮询系统进行解析时,具有一定的困难度.而本文采用的对称与非对称相结合的混合服务模式,在对其性能解析过程中有着巨大的挑战性.同时,多队列的非对称轮询服务的二阶特性(平均等待时间)很难给出其精确的数学解析式,所以选择一种合理的近似方法去解析平均等待时间是研究非对称性轮询服务最关键的一点.

针对以上的分析过程,本文首先建立两级优先级非对称性的服务模型,给出一阶特性量平均排队队长及循环查询周期的精确表达式.然后对模型的二阶特性量进行分析,并且参照文献[8]运用查询周期的二阶特性近似相等的方法,对平均等待时间进行解析.最后在软件Matlab中进行实验仿真,并与理论计算结果进行对比.本文在构建数学模型当中,则是采用了完全的调度策略服务于中心队列,而普通队列则采用了非对称的门限服务的方式.在服务的过程当中,服务器优先对高优先级的中心队列进行发送服务,直到中心队列所存在数据信息量为空时,服务器会转换到第i(i=1,2,···,N)个普通队列,因为该服务模型由中心队列转换到普通队列时,采用的是并行服务模式,所以当服务器由中心队列转向对普通队列进行服务时,就不需要再经历一个查询转换时间,而是直接转向普通队列对其进行服务.当普通队列i的数据信息量完成发送之后,服务器会经历一个查询转换时间再一次转向中心队列,对其进行完全服务,当中心队列的发送服务完成之后,第i+1个普通队列将会得到服务,该模型的查询顺序如下图2所示.服务器采用两种混合式的轮询服务,可以让中心队列获得更多的服务时间,实现了中心队列与普通队列之间优先级的区分,同时也保证了一般的业务能够得到普通队列的服务[10].

1 系统模型

两级优先级非对称轮询控制系统的控制机制是由一个服务器及N+1个队列来构建组成的,N+1个队列中包括N个普通队列和一个中心队列[9],分析过程中则用h来对中心队列进行代替.因为两级优先级非对称轮询系统,是一种对称与非对称相结合的混合式轮询服务系统,在这种服务模式中,中心队列由1个队列构成,在每一次轮询服务的过程中,其自身的性能参数都是固定不变的,这在局部的意义上可以说是一种对称性的体现;此外,由于多个普通队列中,每个队列都有其独立不同的性能参数(到达率、服务时间、转换时间)设置,体现多个普通队列之间所存在的非对称性,所以需要对中心队列和普通队列,分别采用两种不同的轮询服务.

图1 两级轮询服务模型Fig.1 Two-level polling service model

图2 系统的查询服务顺序Fig.2 System query service sequence

设定在tn时刻队列i(i=1,2,···,N)接受到服务器的发送服务,第i个队列中所包含的数据信息量为ξi(n),定义系统的随机变量为{ξ1(n),ξ2(n),···,ξN(n),ξh(n)}, 其所耗费的服务时间定义为νi(n).队列在接受服务期间不断地会有数据信息量加入队列,在此时间段到达第j(j=1,2,···,N,h)个队列的数据信息量为ηj(νi).服务器所提供给普通队列的服务完成之后,会经过一个查询转换时间,在时刻服务器为中心队列h提供发送服务,此刻中心队列中所存在的数据信息量为ξh(n∗),定义系统的随机变量为{ξ1(n∗),ξ2(n∗),···,ξh(n∗),ξh(n∗)}. 中心队列h需要的服务时间定义为νh(n∗),队列中的数据信息量采用完全服务的方式期间,进入到第j(j=1,2,···,N,h)个队列的数据信息量为ηj(νh).服务完成之后,在tn+1时刻第i+l个普通队列开始接受服务,定义随机变量{ξ1(n+1),ξ2(n+1),···,ξN(n+1),ξh(n+1)}.服务器经第i个队列转换到中心队列,再经中心队列转换到第i+l个队列,其所耗费的转换时间为µi(n),在此时间段加入到第j(j=1,2,···,N,h)个队列的数据信息量为µj(µi),轮询系统的随机变量存在以下关系为

1.1 工作条件

1)在任何时刻加入队列的数据信息量服从于彼此独立的、且同分布的泊松过程,其分布概率母函数为Ai(zi),均值为,方差为其中i=1,2,···,N;中心队列的分布为.

2)服务器对任意一个队列进行发送时,队列中所包含的数据信息量在发送的时候所耗费的时间满足于彼此独立的、且同分布的过程,其分布概率母函数为Bj(zj),均值为,方差为,其中j=1,2,···,N;中心队列的分布为.

3)服务器完成队列的发送服务,队列之间进行切换时,所耗费时间的分布过程的概率母函数为Rk(zk),均值为,方差为,其中k=1,2,···,N;中心队列的分布为.

4)设定服务系统中任何一个队列的缓存容量足够大,不存在数据信息量丢失的情况发生;

5)每一个加入进队列的数据信息量,将会按照先到先服务(First come first served,FCFS)的方法接受服务[11].

1.2 系统分析定义的变量

ui(n):第i个普通队列在接受完服务之后,查询转换到中心队列所耗费的时间;

vi(n):服务器完成对第i个普通队列中数据信息量的发送服务所耗费的时间;

vh(n∗):服务器完成对中心队列所包含的数据信息量的发送服务所耗费的时间;

µj(ui):设定为在ui(n)这段时间长度内加入进第j个队列的数据信息量;

ηj(vi):设定为vi(n)这段时间长度内加入进第j个队列的数据信息量;

ηj(vh):设定为在vh(n∗)这段时间内加入进第j个队列的数据信息量.

概率母函数定义为

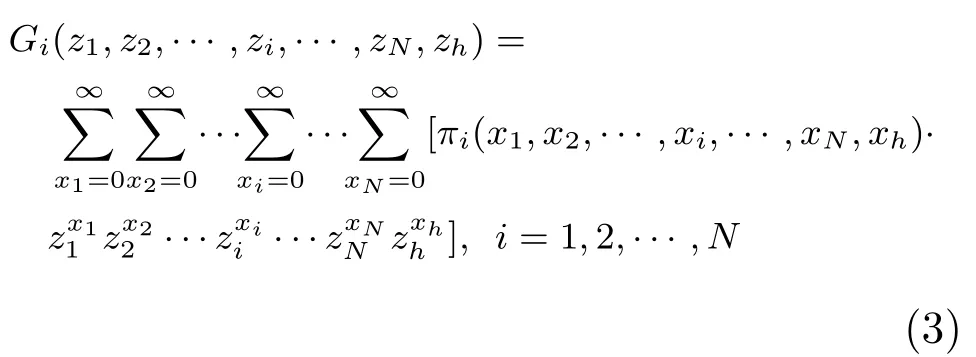
在tn∗时刻系统状态变量的概率母函数为

在tn+1时刻系统状态变量的概率母函数为

式中,Fi(zi)=Ai(Bi(ziFi(zi))),i=1,2,···,N表示服务器对任意一个队列,在任一时段内到达的数据信息量以及在服务期间到达的数据信息量使用完全服务的方式所需时间的随机变量的概率母函数[13].

2 轮询系统的一阶和二阶特性

2.1 平均排队队长

根据式(4)和式(5)求得第i个普通队列的平均排队队长的表达式为

同理,采用上述方法可以得到中心队列的平均排队队长的表达式为

gih(h)表示为普通站点i所有的数据信息量接受完服务,转换到中心站点之后,这段时间内以及在服务期间进入中心站点的所有数据信息量的平均排队队长,所以在以下对中心队列进行分析时会出现多段各不相同的平均排队队长和平均等待时间的情况.

2.2 循环查询周期

轮询系统的循环查询周期表示为:同一队列被服务器前后两次访问时刻的时间差,其具体为N+1个队列按规定的服务规则进行一次服务所花费时间的统计平均值[14].所以可以计算得到两级非对称轮询系统的循环周期E(θ).

2.3 二阶偏导量

定义:

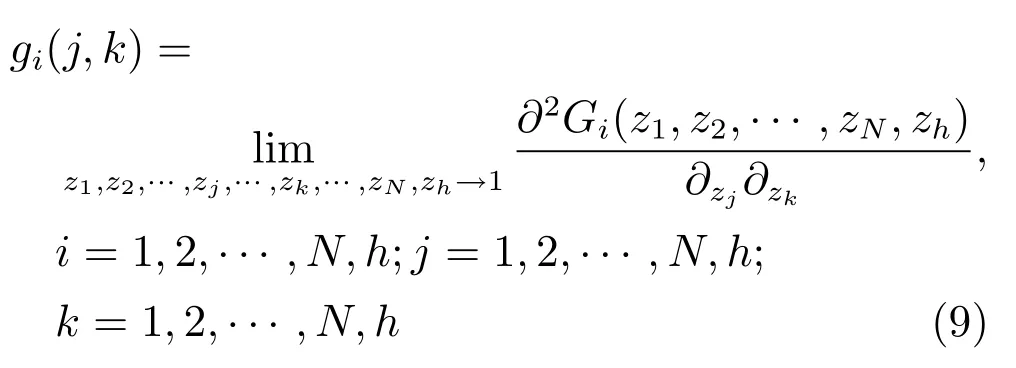
则由式(4)和式(5)可以得到以下二阶偏导量:

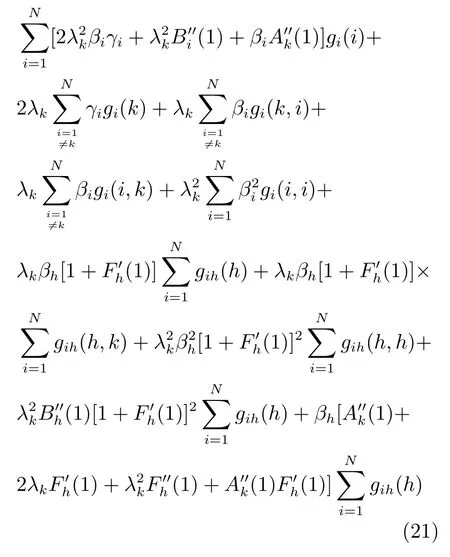
将式(18)求和,并利用式(20)化简得到

2.4 基于循环查询周期的近似分析方法

根据循环查询周期的定义得到该随机变量的概率母函数为θi(zi),并有如下关系式:

对此式进行二阶求导,得到

因为系统的二阶特性量有

根据式(22),式(24)及式(25)得到

根据式(26)并分别结合式(22)和式(18)可以得到gih(h,h)和gi(i,i)的近似表达式.

2.5 平均等待时间

信息分组的平均等待时间是指数据信息量到达队列被发送出去所需的时间.根据上述计算得到的gi(i,i)和gih(h,h)的近似表达式,分别代入下面两式即可求得平均等待时间的表达式.

普通站点的平均等待时间为

中心站点的平均等待时间为

3 仿真实验及性能分析

基于上述所建立的两级优先级非对称轮询服务模型,同时根据以下所建立的工作条件进行理论值计算和实验仿真[15−16].

1)各队列的参数变量都应当服从相同的分布,但是各变量并不具备对称性;

2)任一时隙内进入各队列的数据信息量都满足Poisson分布;

根据如下表1中所设置的初始参数的基础之上,得到以下图中服务模型性能特点的变化情况.

表1 服务模型的基础参数Table 1 Basic parameters of the service model

图3与图4展示了普通队列与中心队列的平均排队队长随到达率变化的情况,从图中可以看出在到达率不断增加的情况下,普通队列服从于与到达率相同的变化规律,即到达率变大其也会随之而变大,当然中心队列亦满足此种变化形式.同时,可以从图中分析得到高优先级的队列与低优先级队列的队长之间的区分度是比较高的,受到达率影响的情况下,低优先级的队长都远大于高优先级的队长.

图3 普通队列平均排队队长随到达率影响变化(N=5)Fig.3 The average queue length of ordinary queue varies with arrival rate(N=5)

图4 中心队列平均排队队长随到达率影响变化(N=5)Fig.4 The average queue length of central queue varies with arrival rate(N=5)

图5 普通队列平均排队队长随服务时间影响变化(N=5)Fig.5 Variation of average queue length with servicetime in ordinary queue(N=5)

从图5与图6可以看出普通队列与中心队列的平均排队队长受服务时间的影响比较明显,服务时间增加时队长也会随之而变大.同样,两种具有不同优先级的队列,其平均排队队长有着很大的差别,很好地说明了轮询系统的优先级得到了较好的区分.除此之外,图中1至h与5至h这两段时长的中心队列的平均排队队长的增长率与其他几个队列相比是比较小的.主要原因则由各队列到达率的不同而引起的,这与理论分析相一致,由式(6)可以看出中心队列的队长与到达率成正比关系,所以这两段时长到达率较小时,给中心队列的队长带来的影响较小.

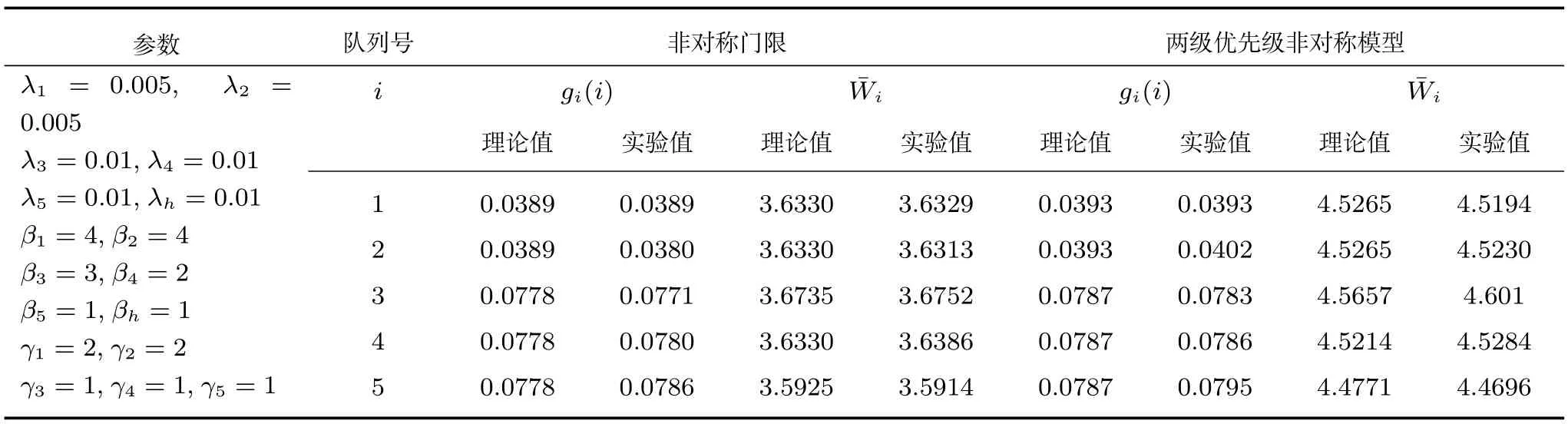
表2 两种模型理论值与实验值的对比Table 2 Comparison between theoretical values and experimental values of two models

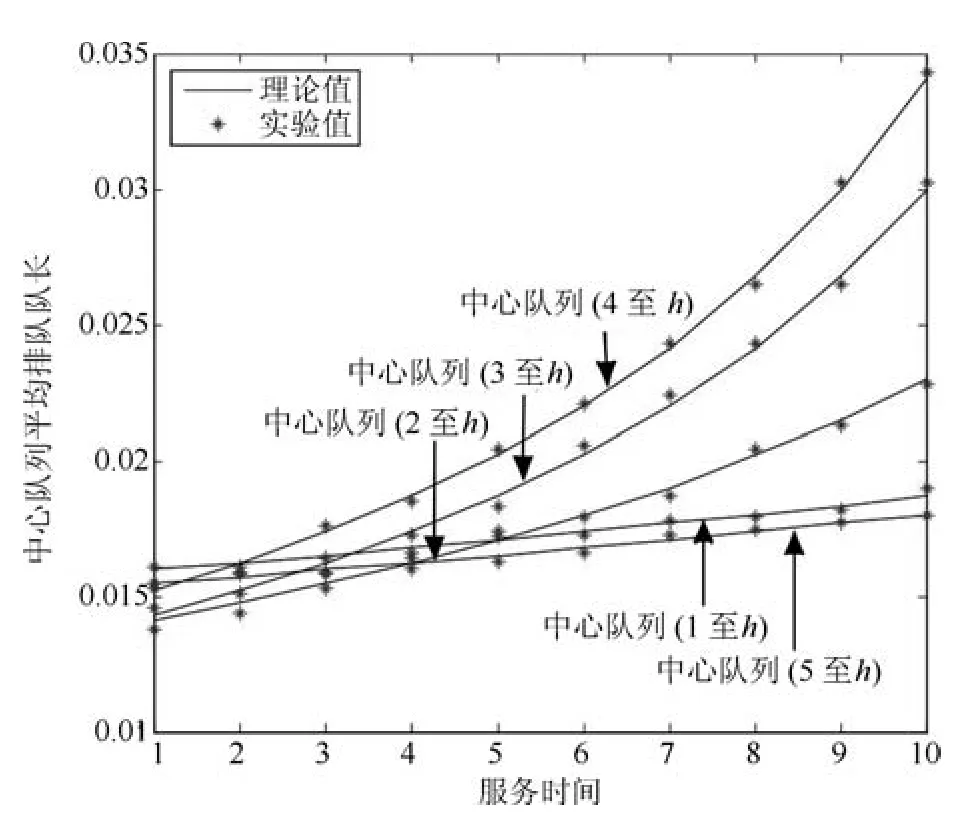
图6 中心队列平均排队队长随服务时间影响变化(N=5)Fig.6 The average queue queue length of central queue varies with service time(N=5)

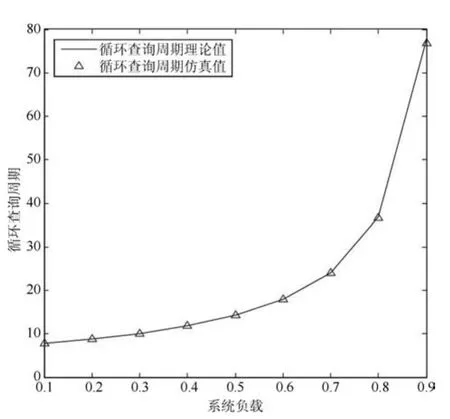
图7 循环查询周期随系统负载影响变化(N=5)Fig.7 Cyclic query cycle varies with system load(N=5)

图7中系统的负载是指普通队列的总负载,并不包含中心队列的负载,主要是为了方便仿真图形的构建,并与其他非对称模型形成对比,此外需要说明的是中心的负载的改变,同样会对系统的特性产生影响.图7至图8也是如此情况.从图6中可以看出,轮询系统的循环查询周期随着负载的增大而不断变大,同时,循环查询周期的理论值与实验值之间有着较好的稳合性.

从图8到图9可以看出,当选取的循环次数较大时,平均等待时间的理论值与实验值是保持一致的且误差较小.对于同一系统而言,当系统的负载变大时,平均等待时间也是随之而变大的,同时,系统的队列数增加时这种关系依然存在.系统在同一负载的情况下,中心队列的平均等待时间小于普通队列的平均等待时间,这也很好地说明采用混合的轮询服务方式来进行优先级的区分,是有显著成效的,使得系统的性能得到了一个整体优化.综上所述,该服务模型运用循环查询周期二阶特性近似相等的方法得到了平均等待时间的近似解.该种近似方法运用在本文所建立的模型当中,比较适用于达到率较小的情况,同时,当系统的负载相对较高时,理论值与实验仿真值的误差就会相对变大,此时需要考虑该分析方法的容错范围.

表2中展示了非对称门限服务与本文所提出模型的性能特性比较,从表2中可以看出当两级优先级非对称轮询模型普通队列的总负载与非对称门限服务的总负载在相同的情况下,两级优先级非对称模型的平均排队队长和平均等待时间都略大于非对称门限的两种特性,从另一方面也说明了中心队列的负载可以影响整个系统的服务特性,所以对非对称性的轮询服务系统进一步进行优先级的区分,可以让具备更高优先级的队列获得更多的服务时间和更高的服务效率.此外两种非对称性的模型理论值与实验值之间都有着较好的吻合性,误差较小,说明了两种非对称模型的服务特性得到了较好的解析,进一步验证了模型解析过程的正确性.

图8 普通队列平均等待时间受负载影响变化(N=5)Fig.8 Average waiting time of ordinary queues is affected by load changes(N=5)

图9 中心队列平均等待时间受负载影响变化(N=5)Fig.9 The average waiting time of the central queue is affected by load changes(N=5)

4 结论

本文采取了一种对称性轮询服务与非对称轮询服务相结合的区分优先级的轮询服务,即在具有低优先级的普通队列采用非对称的门限服务,在具有高优先级的中心队列使用对称性的完全服务.为了提高系统的利用率,所以本文选择了非对称性的轮询服务,并且运用并行模式的服务机制构建了两级优先非对称服务模型.服务模型的平均排队队长和循环查询周期,得到了精确的解析.经过大量的实验分析,使用了一种较为合理的方法较优的对系统的二阶特性量,平均等待时间进行了解析.并通过仿真实验实验与理论分析相比较,验证了模型解析过程的正确性.

除此之外,需要说明的是此模型二阶特性量的近似方法并不局限于本文中所使用的分析方法,还有许多的近似方法值得我们去进一步探索,去找到一种更优的方法来对平均等待时间进行解析.当然,在未来工作当中,对其他的一些非对称性混合服务模型,如对称性完全–非对称性完全、限定–非对称性门限、门限–非对称性门限等区分优先级的两级非对称服务模型进行探讨是非常有意义的.