倒数模型在纯滞后控制系统中的应用探讨
2018-04-23刘尚标
刘尚标
(本溪北方工业装备有限责任公司,辽宁 本溪 117000)
0 引言
为了解决具有纯滞后特性被控对象受控难的问题,Smith于1957年提出了史密斯预估模型,Garcia和Morari于1982年提出了内模控制算法。后有学者证实内模控制算法是史密斯预估模型的一种特殊表现形式[1]。但就控制效果而言,史密斯预估模型优于内模控制算法。史密斯预估模型和内模控制算法应用的前提,是建立被控对象的数学模型,且所建立的数学模型与被控对象一致性越高,其控制效果越好[2-5]。在工业现场,尤其对于较为复杂的被控对象,建立被控对象的数学模型非常困难。
为此,本文设计了一种简便模型。其不依赖于现场工程师对被控对象求取数学模型,而是将被控对象直接纳入该模型内,通过模型自身的转换,得到被控对象传递函数的倒数。该模型本文称之为倒数模型。利用常规PID控制倒数模型,间接实现对具有纯滞后特性被控对象的控制。
1 模型可倒原因分析
被控对象数学模型不完全可倒的主要原因[6]如下。
①数学模型中含有非最小相位环节(即其零点在右半平面),其倒数会形成不稳定环节。
②数学模型中含有纯滞后环节,其倒数为纯超前,无法实现物理纯超前。
对于以上原因分析如下。
①含有非最小相位环节被控对象的倒数闭环负反馈系统能稳定运行。
②虽然无法实现纯超前,但被控对象的倒数可避免纯滞后环节影响。
③通过对被控对象倒数的调节,间接实现对被控对象的调节。
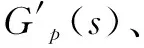
(1)
(2)
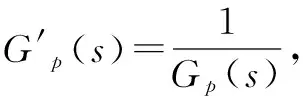
(3)
比较式(1)和式(3)可知,闭环极点相同,说明被控对象的倒数的闭环负反馈系统不改变系统的稳定性。由此可得如下结论:若被控对象的闭环负反馈系统稳定,则该被控对象的倒数闭环负反馈系统也稳定,而与该被控对象是否含有非最小相位环节无关。
2 建立倒数模型
倒数模型如图1所示。

图1 倒数模型框图 Fig.1 Block diagram of the reciprocal model
图1虚线框内所示传递函数为:
(4)
由此可知,图1所示传递函数为:
(5)
由式(5)可知,图1所示倒数模型可以实现被控对象的倒数关系转换。该模型由内外两个环节组成。
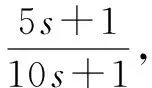
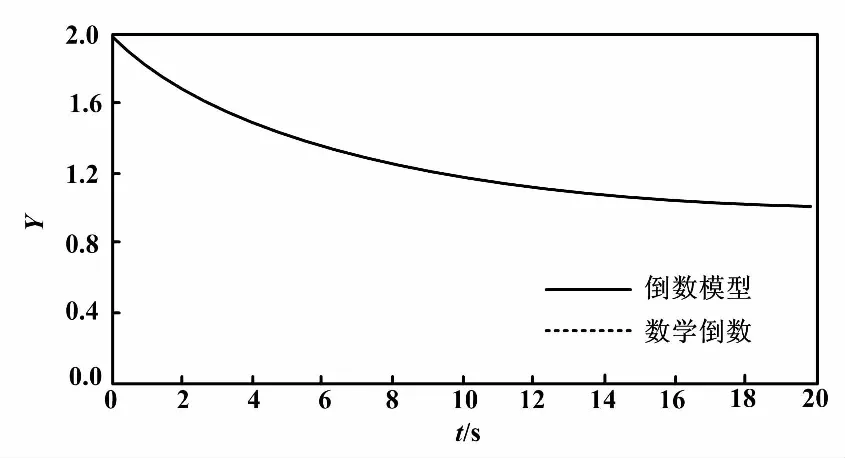
图2 倒数模型与数学倒数阶跃响应效果对比图 Fig.2 The contrast of step response of the reciprocal model and the mathematical reciprocal
由图2可知,被控对象的倒数模型阶跃响应曲线与被控对象数学倒数的阶跃响应曲线完全重合。由此进一步验证了该倒数模型可以实现被控对象的数学倒数转换。
3 建立倒数模型的闭环负反馈控制系统模型
倒数模型闭环负反馈控制系统框图如图3所示。

图3 倒数模型闭环负反馈系统框图 Fig.3 Block diagram of negative closed loop feedback system of the reciprocal model
由前述结论可知,若含有非最小相位环节被控对象的闭环负反馈系统可稳定运行,则该被控对象倒数的闭环负反馈系统亦可稳定运行。由此考虑为倒数模型引入闭环负反馈环节,来保证可能含有非最小相位环节的倒数模型可以稳定运行。同时考虑在闭环倒数模型的外环添加积分环节,实现对内环的预补偿。最终通过对被控对象倒数的调节,来间接实现对被控对象的调节,以改善纯滞后控制系统的控制品质。

由图3可知,倒数模型的闭环负反馈控制模型的传递函数方程如下:
Y(s)={[R(s)-Y(s)]Gc(s)+Y(s)}×
(6)
假设外环积分环节完全实现了对内环的补偿,则下式成立。
(7)
即:
(8)
首先分析系统输入对系统输出的影响。令N(s)=0,将式(8)代入式(6),整理后得:
Y(s)[Gc(s)+Gc(s)kGp(s)]=
R(s)[Gc(s)+Gc(s)kGp(s)]
(9)
即:
Y(s)=R(s)
(10)
由式(10)可知,系统输出完全根据系统输入变化而变化。
分析外界扰动对系统输出的影响。令R(s)=0,将式(6)整理如下:
(11)
将式(8)代入式(11),得:
(12)
(13)
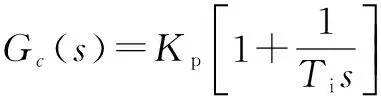
(14)
由式(14)可知,TiTa越小,扰动对输出的影响越小,即系统的抗干扰能力越强。由此可知,模型参数整定时,应将Ta整定得足够小,以提高系统的抗干扰能力。
总之,倒数模型外环积分环节的引入,不仅使得系统的输出可以很理想地跟随输入的变化而变化,还可以抑制扰动对系统输出的影响。倒数模型外环积分环节对改善系统控制品质起到至关重要的作用。仿真试验验证该结论是正确的。

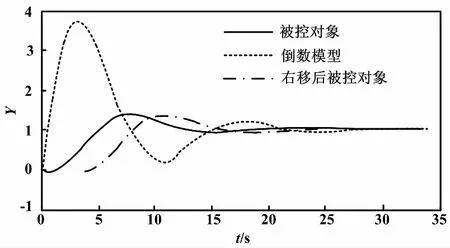
图4 含非最小相位环节被控对象阶跃响应效果对比图 Fig.4 The contrast of step response of the controlled object with nonminimum phase
由图4可知,由于引入积分环节,倒数模型闭环负反馈系统的倒数模型与被控对象幅值不存在倒数关系,但其曲线趋势仍保持倒数关系,只是相对倒数模型响应被控对象响应提前。
4 控制效果对比

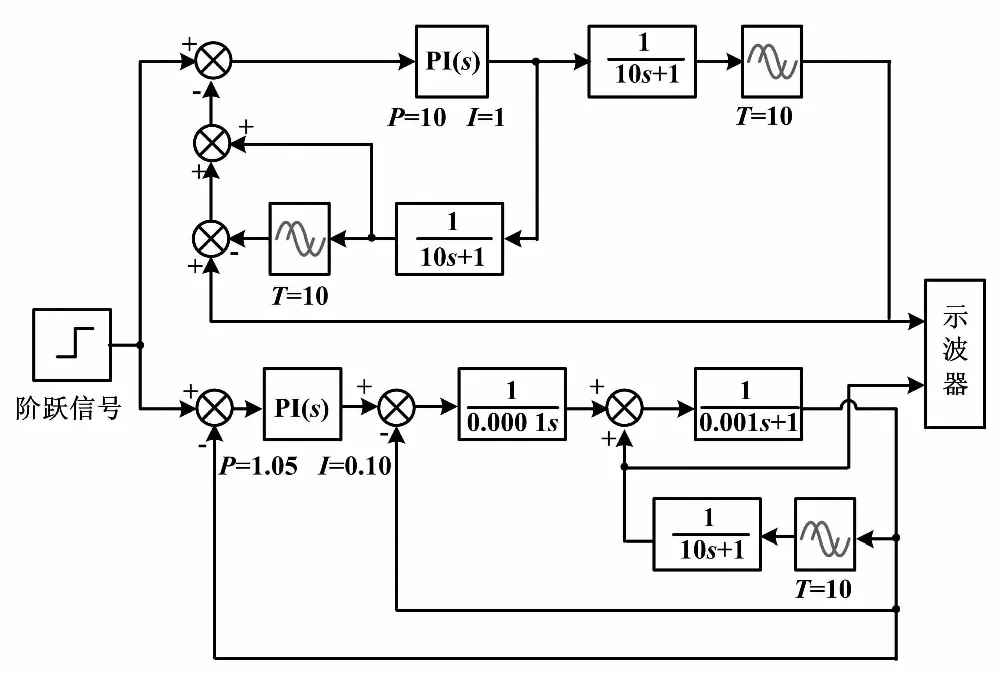
图5 仿真系统框图 Fig.5 The system block diagram of simulation
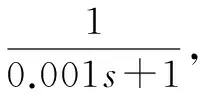
倒数模型与史密斯预估模型阶跃响应效果对比图如图6所示。

图6 倒数模型与史密斯预估模型阶跃响应效果对比图 Fig.6 The contrast of step response of the reciprocal model and the Smith predictive model
由图6可知,在倒数模型系统中,由于已经实现了对被控对象的预补偿,故其响应曲线基本与阶跃响应等同,只是受滞后时间影响,曲线整体后移而已。
仅改变图5中倒数模型系统被控对象纯滞后项时间常数的仿真效果对比图如图7所示。
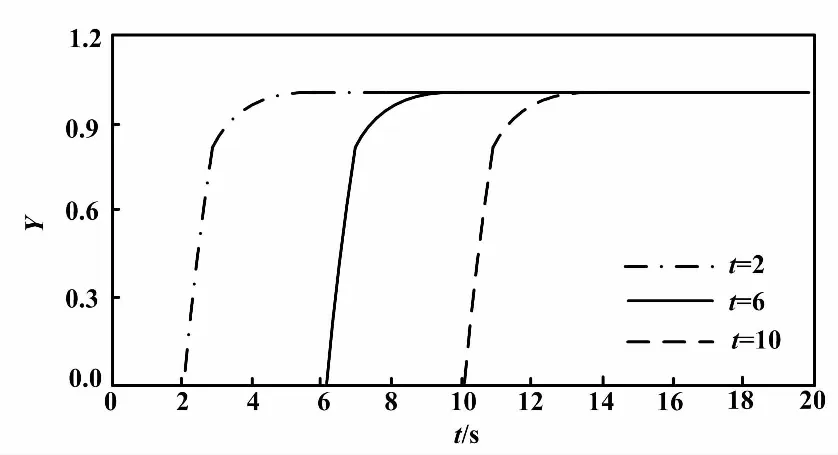
图7 改变纯滞后项时间常数阶跃响应效果对比图 Fig.7 The contrast of step response of changing time constant of the pure time-delay
与史密斯预估模型阶跃响应效果对比可知,倒数模型系统阶跃响应平衡过渡时间更短,其阶跃响应效果更为理想。由于史密斯预估模型受预估环节的限制,其无法适用于纯滞后项时变系统[8-9]。而倒数模型设计的初衷就是想规避被控对象纯滞后项对控制的影响,故其完全适用于纯滞后项时变系统。
5 结束语
由以上分析可知,倒数模型的闭环负反馈系统适用于具有纯滞后特性的被控对象,其控制效果要优于史密斯预估模型。该系统的优点在于控制结构简单、参数设置方便,并且适用于纯滞后项时变系统。由于其应用不必以得到被控对象数学模型作为前提条件,故其更利于在工业现场的推广应用。其缺点在于受模型控制机理限制,倒数模型仅适用于非滞后项为大惯性自衡系统。
参考文献:
[1] 谷俊杰,张栾英.关于内模控制的一些研究[J].计算技术与自动化,1983,12(1):24-26.
[2] 王春民,刘兴明,嵇艳鞠.连续与离散控制系统[M].北京:科学出版社,2008.
[3] 张翼飞,曾亮,邓方林.时滞系统控制发展历程综述[J].控制工程,2004,11(S1):4-7.
[4] 周涌,陈庆伟,胡维礼.内模控制研究的新发展[J].控制理论与应用,2004,21(3):475-482.
[5] 陆平,赵捷,郭鹏.模糊内模PID控制与应用[J].自动化仪表,2012,33(3):50-52.
[6] 王树青.工业过程控制工程[M].北京:化学工业出版社,2002.
[7] 耿华,杨耕.控制系统仿真的代数环问题及其消除方法[J].电机与控制学报,2006,10(6):632-635.
[8] 刘桂香,陈菊,朱学峰,等.自适应修正Smith算法控制大时滞过程的仿真研究[J].控制理论与应用,2008,27(10):12-14.
[9] 雷正桥.大时滞参数时变复杂过程的仿人智能控制[J].自动化仪表,2016,37(3):74-76.
