8阶三正则图的分类研究
2018-04-20
(武汉船舶职业技术学院,湖北武汉 430050)
1 4阶三正则图
为了讨论方便,先假设,文中提到的图皆为简单连通图。
定理1.1三正则图的阶数一定是大于等于4的偶数。
证明设三正则图的边数为m,顶点数为n,由握手定理有:3n=2m。由此可见n必须是偶数。由于2阶非简单连通的三正则图不存在。所以n一定是大于等于4的偶数。
定义1一个简单连通图称为是顶点同圆周的,如果它的所有顶点都可以画在同一圆周上,并且保持点边的关联关系不变。
由定义可知:一个顶点同圆周的图画成顶点同圆周而得到的图和原来的图是同构的。
定理1.2 一个简单连通图是顶点同圆周周的当且仅当它是Hamilton图。
定理1.3(Dirac 1952)设G是n(≥3)阶简单图连通图,如果对于G的任意顶点v都有deg(v)≥n/2,则G是Hamilton图[1]。
定理1.4在同构的意义下,4阶三正则图只有一个。
证明由定理1.3可知:4阶三正则图是顶点同圆周的。设它的顶点分别为A,B,C,D。如图1(a)所示。因为是简单图连通图,所以A和B不能再有边连接,A和D也不能再有边连接,当然更不能出现环。因此,只能是图1(b)的连接方式。
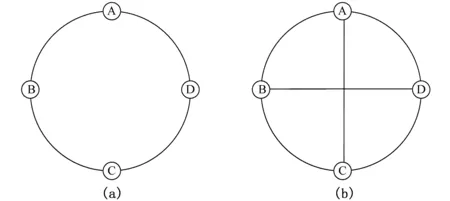
图1 4阶三正则图的形成
定理1.54阶三正则图是个平面图,非二部图,非Euler图。
实际上,4阶三正则图就是K4。注意:不存在非连通的简单4阶三正则图。图2是4阶三正则图的其它几种画法。
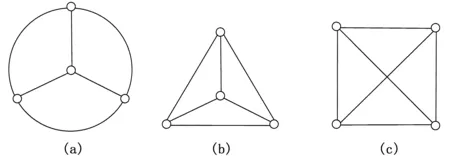
图2 4阶三正则图的其它几种画法
2 6阶三正则图
仿前面的做法,有下面的定理。
定理2.1在同构的意义下,6阶三正则图只有两个。它们分别是K3,3和三棱柱。
如图3(a)和图3(b)所示,它们分别是K3,3和三棱柱。
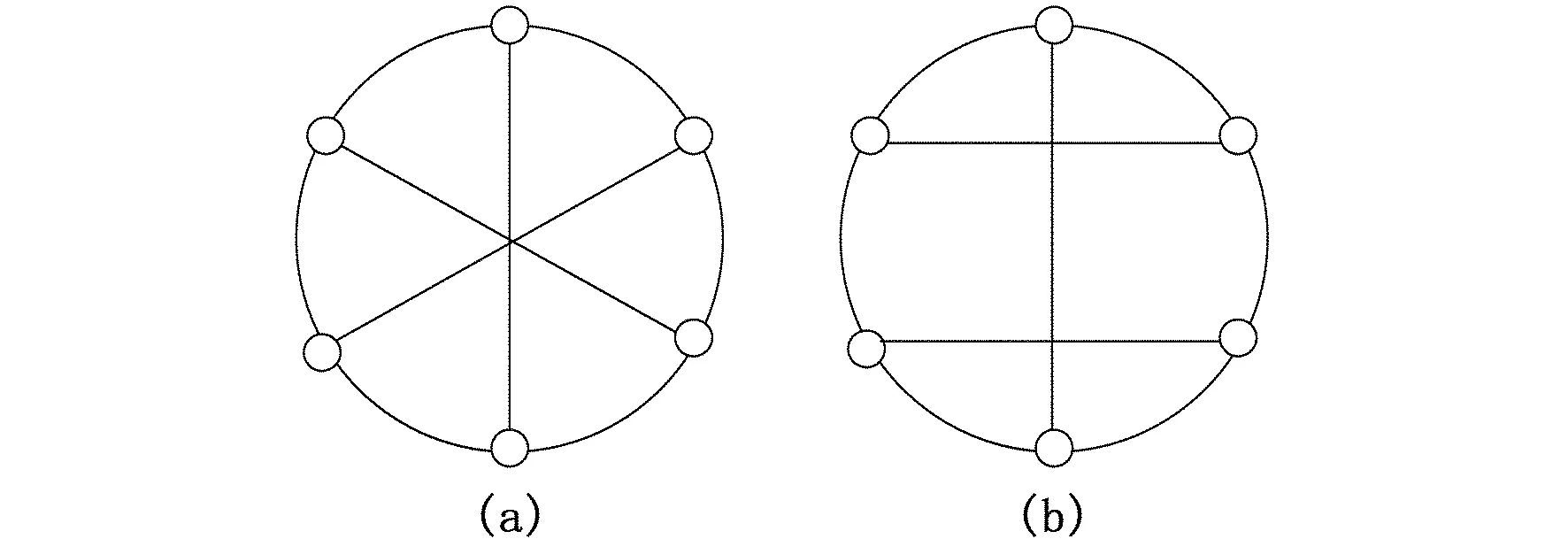
图3 6阶三正则图
图4是K3,3的其它画法。
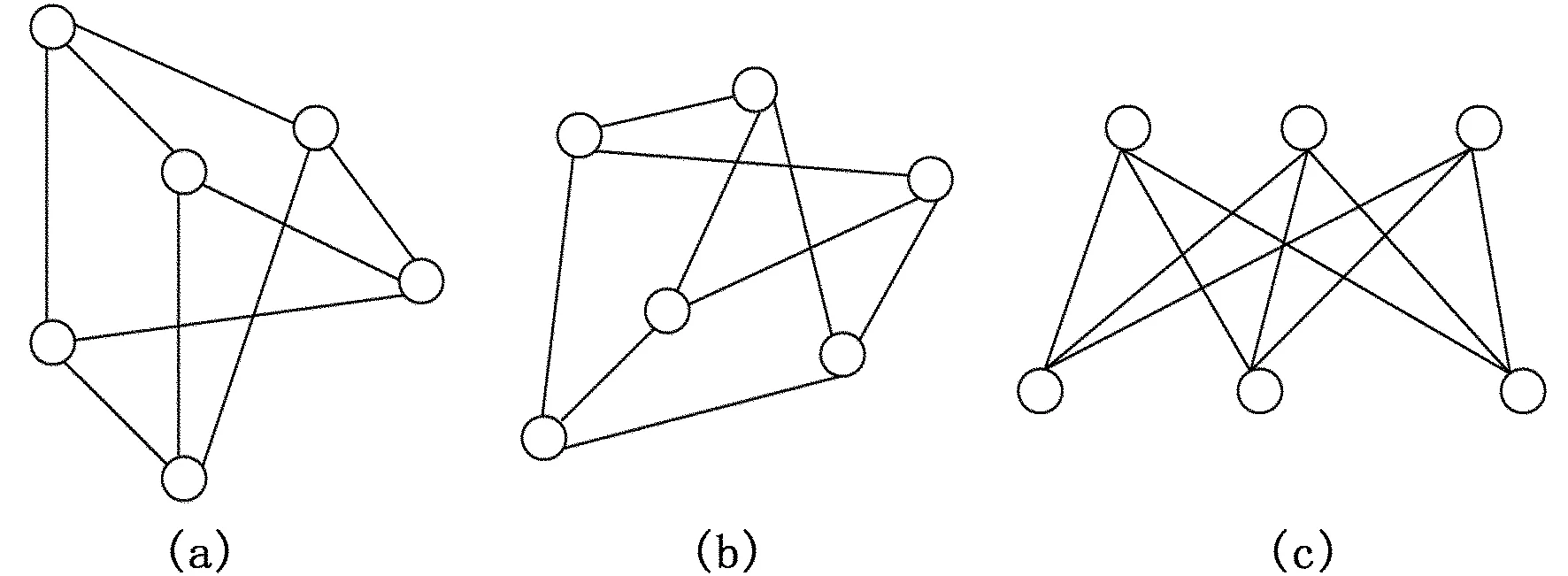
图4 K3,3的其它几种画法
定理2.2K3,3是Hamilton图,非可平面图,是二部图,非Euler图。
定理1.3保证了K3,3是Hamilton图。
图5分别是三棱柱的其它画法。
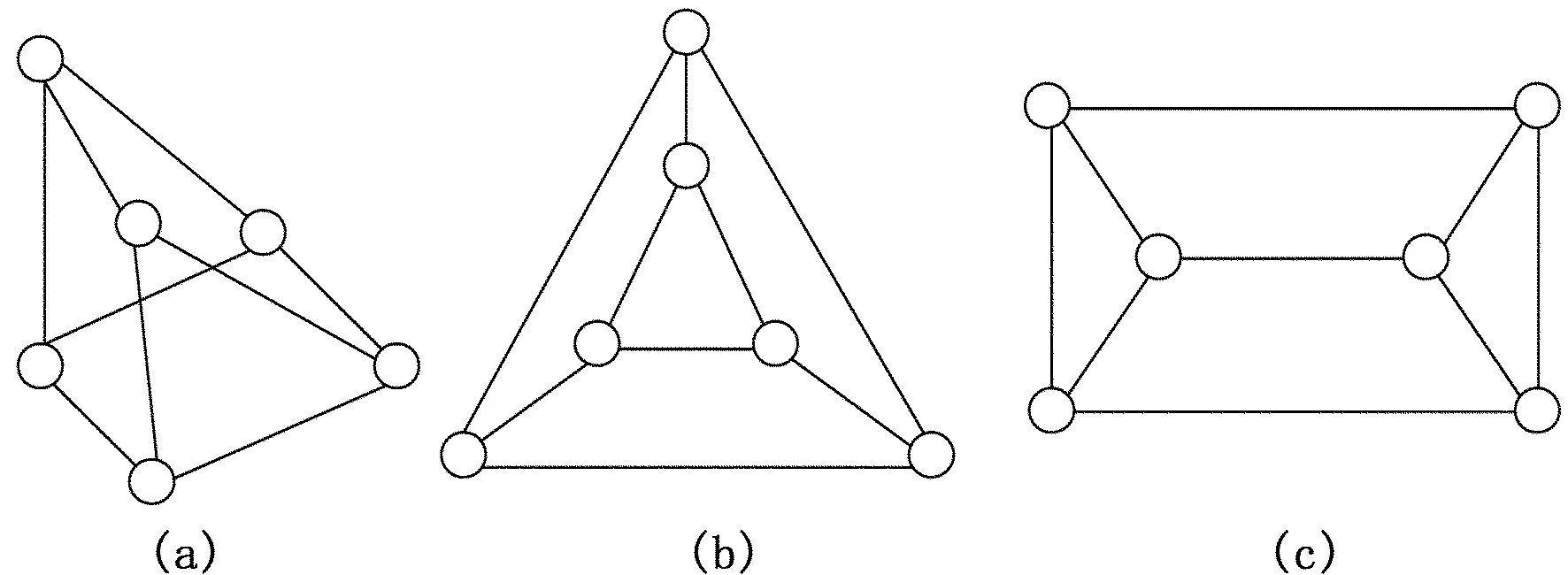
图5 三棱柱的其它几种画法
定理2.3三棱柱是Hamilton图,是可平面图,非二部图,非Euler图。
定理1.3保证了三棱柱是Hamilton图。
定理2.4设G为n(≥3)阶图,若对于图G中任意两个不邻接的顶点u和v,都满足:degu+degv≥n-1,则G是连通的,且diam(G)≤2[1]。
推论设G为n(≥3)阶图,若δ(G)≥(n-1)/2,则G是连通的[1]。
有了定理2.4及其推论,可以断言:不存在非连通的6阶立方体。
3 8阶三正则图
定理3.1在同构的意义下,顶点同圆周的8阶三正则图只有五类。分别是第Ⅰ类,第Ⅱ类,第Ⅲ类,第Ⅳ类和第Ⅴ类。图6是顶点同圆周的8阶三正则图。
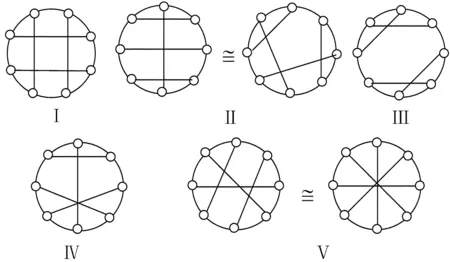
图6 五类8阶三正则图
定理3.1的证明思路如图7所示。推理过程中利用了三正则的条件。
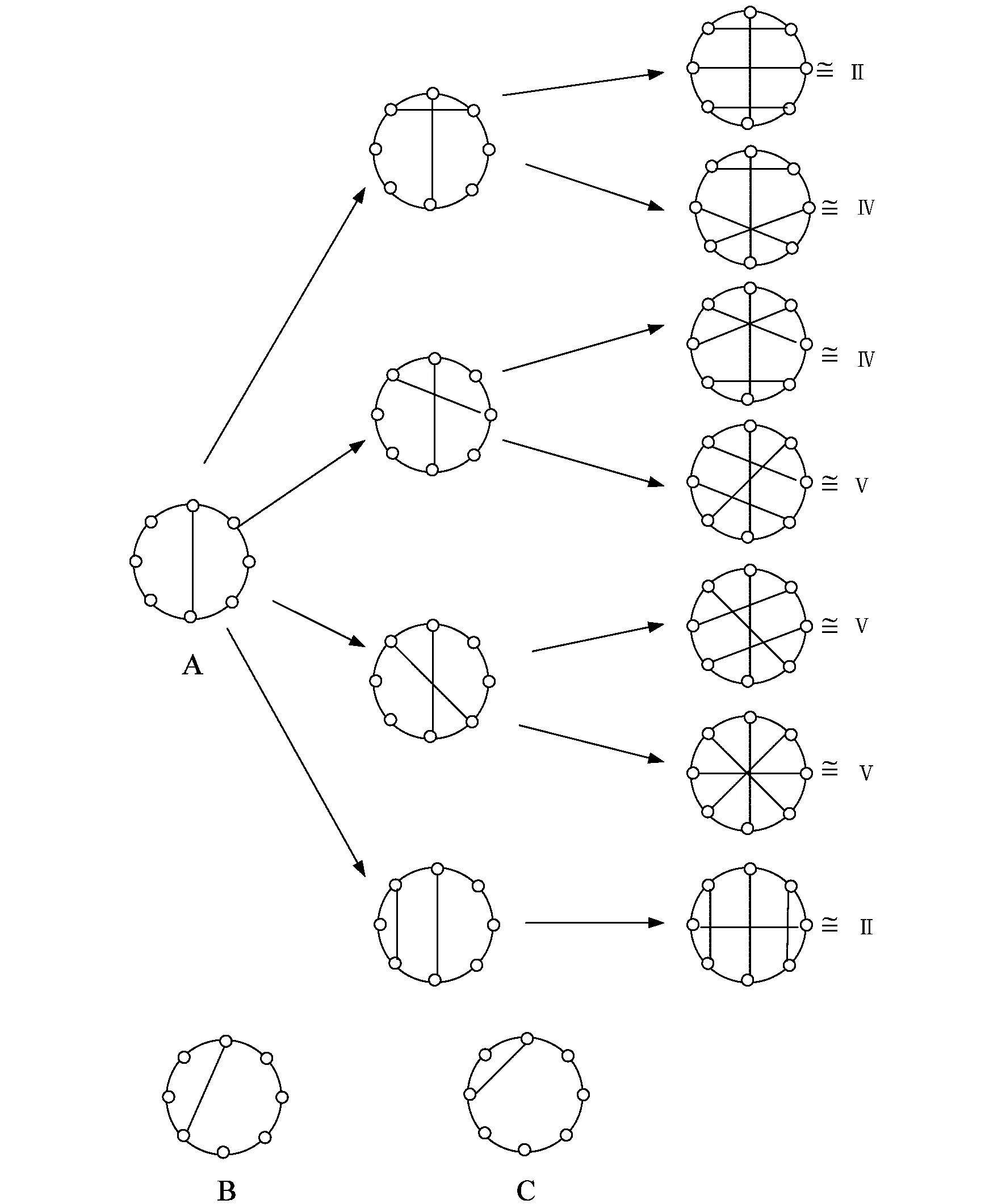
图7 定理3.1的证明思路
类似的可以讨论情况B和情况C,只有三种情况。最后可以得出五类顶点同圆周的8阶三正则图。
定理3.2简单连通的8阶三正则图是无桥图。
证明(反证法) 设图G是存在桥的简单连通的8阶三正则图。u,v是图中桥的两端点。现在把桥去掉,u,v也去掉,而把连接u的两顶点用边连接起来,同样把连接v的两顶点也用边连接起来。这样就得到了两个图,它们都是简单连通三正则图,由定理1.1,这两个图的顶点数加起来至少是8,因此图G至少是10阶的,这与图G是8阶的矛盾。故简单连通的8阶三正则图是无桥图。
定理3.3若图G满足:δ(G)≥2,则图G包含一个圈[2]。
定理3.4简单连通的8阶三正则图是Hamilton图。
证明设图G是简单连通的8阶三正则图。由定理3.3,图G存在圈。下面证明:若图G中存在长度为n(3≤n<7)的圈,则图G中存在长度大于n的圈。
n=4时,证明思路如图8所示。利用无桥性,如图9(1)中是经过两个顶点返回A点(C点和A点对称)则ABCDEFA是长度为6的圈或B点则BCDEFB是长度为5的圈。其他类推。因此,图G中存在长度为8的圈,故G是Hamilton图。
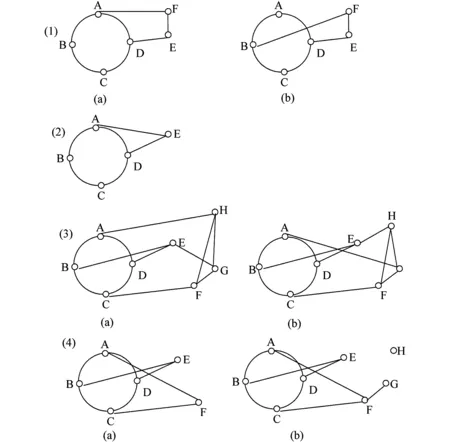
图8 定理3.4的证明思路
注:存在不连通的8阶三正则图。图9给出了不连通的简单8阶三正则图。
图9中六种情况均由两个K4组成的不连通图。
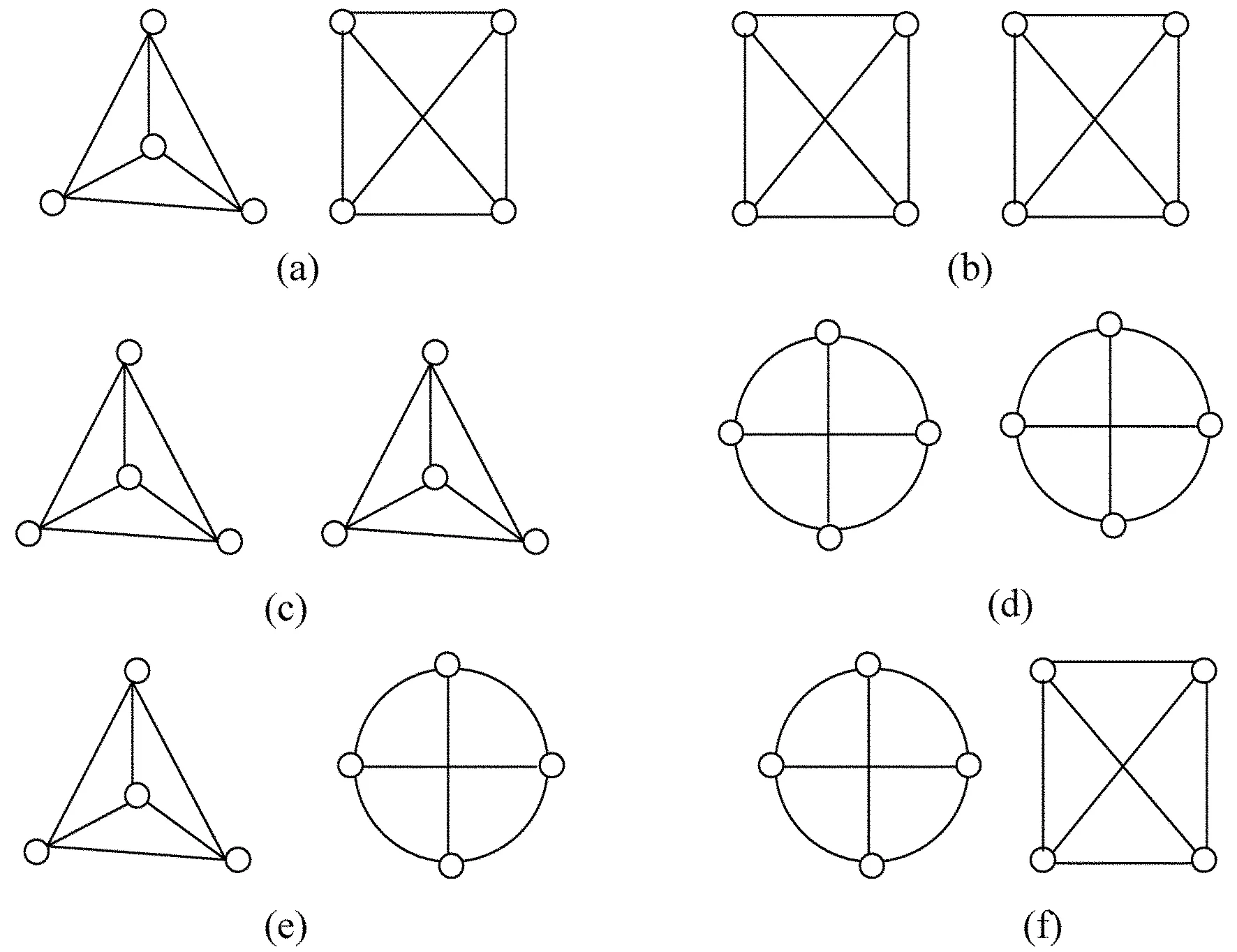
图9 不连通的8阶简单三正则图
1Gary Chartrand and Ping Zhang(美).范益政,汪毅,龚世才,朱明译.图论导引[M].北京:人民邮电出版社,2007:30,130.
2Douglas B.West(美).李建中,骆吉州译.图论导引[M].北京:机械工业出版社,2006:20.
3徐俊明.图论及其应用(2版)[M].合肥:中国科学技术大学出版社,2004.
4张先迪,李正良.图论及其应用[M].北京:高等教育出版社,2004.
5Holton D.A. and J.Sheehan,The Petersen Graph[M].Cambr.Univ.Pr.(1993).
