不同采样方法对细小可燃物含水率预测模型精度的影响

2018-04-20董川成张运林王玉霞

中南林业科技大学学报 2018年5期

张恒，董川成，牛屾，张运林，金森，王玉霞

（1.东北林业大学林学院，黑龙江哈尔滨 150040；2.内蒙古农业大学林学院，内蒙古呼和浩特010019；3.塔河林业局综合勘察设计大队，黑龙江大兴安岭 165200）

林火发生的物质基础和首要条件是森林可燃物，细小可燃物作为森林可燃物的重要组成部分，其含水量的大小直接影响地表可燃物燃烧的难易程度，含水率动态和预测也成为火险天气预报和火行为预报的关键、森林火险等级预报系统的核心[1-3]。气象要素直接回归法[4]作为重要的可燃物含水率预测方法可以考虑到降水、风速和温湿度等气象要素对细小可燃物含水率的影响，早在20世纪20年代就开始与之有关的研究[5]。Gonzalez等[6]建立了基于温度和湿度的多元线性含水率预测模型。Matthews等[7]用温度、湿度、风和太阳辐射来预测桉树可燃物的含水率。我国学者在此方面也已开展了大量的研究，建立了若干森林可燃物含水率气象要素回归预测模型[8-12]。在研究和整理有关细小可燃物含水率的相关文献共51篇的过程中，发现本文所要表达的观点在此前文献数据中得到了论证和支持，即相比之下在以破坏性取样为方法的21篇文献中，其模型拟合度相对较低且误差较低[12-15]，而以非破坏性取样为方法的28篇文献中的研究模型拟合度相对较高[16-18]，其余2篇未提及。2种采样方法究竟对细小可燃物含水率预测模型的精度造成多大的影响？这是我们亟待解决的科学问题。

目前，测定可燃物含水率的方法主要有2种：非破坏性采样法与破坏性采样法。非破坏性采样法是指在样地选取一处或几处固定监测点，在监测点设定标准物，对标准物进行固定时间间隔的连续称质量以获取含水率的方法。破坏性采样法是指每次测定都在样地内随机选取几处测定点，对测定点当时的可燃物称质量进而获取含水率的方法[1-3]。相对来说，非破坏采样法能够克服含水率采样的空间异质性，更好地反映可燃物水分对环境的适应。破坏性采样则具有时效性，但即使取多点平均值，也只能尽量的接近真实值。这2种采样法对于本实验研究地区使用气象要素回归法进行建模时预测精度的影响效果还是未知。搞清楚不同采样方法对细小可燃物含水率预测模型精度有多大的影响，建立科学的含水率预测模型，具有重要的意义。目前该地区进行了许多含水率预测模型的研究[10,12,26-30]，但对于这项研究还没有开展。因此，本研究以大兴安岭3种主要林型内的地表可燃物为研究对象，分析不同采样方法对细小可燃物含水率预测模型精度的影响，为提高气象要素法的预测精度和更准确地预测森林火险提供科学依据。

1 材料与方法

1.1 研究区概况

研究区位于大兴安岭塔河林业局盘古林场（52°41′57.1″N，123°51′56.5″E），地貌为大兴安岭石质中低山山地。该地属寒温带大陆性季风气候，且山地气候特征明显。冬季寒冷而漫长，年均气温-5 ℃。年降水量为350～500 mm，降水集中于7—8月。林内雪深30～50 cm，积雪期达5个月，相对湿度为70%～75%。天气变化较剧烈，常出现高温低湿及大风天气。地带性土壤类型为棕色针叶林土。植被类型是以兴安落叶松为优势的寒温带针叶林[31-32]，主要林分类型为兴安落叶松Larix gmelinii-樟子松Pinus sylvestrisvar.mongolica-白桦Betula platyphylla混交林、樟子松林、白桦林和山杨Populus davidiana林，还有少量的红皮云杉Picea koraiensis林。春季和秋季为森林防火多发期。

1.2 凋落物含水率和气象因子的监测

可燃物含水率监测时间为2010年春季防火期和秋季防火期。其中，2010年5月29日—6月27日为春季森林防火期，9月23日—10月13日为秋季森林防火期。在阳坡选择樟子松林、兴安落叶松林和白桦林3种林分设置样地，记录样地基本情况，详见表1。

表1 样地信息Table 1 Information of sampling plots

1.2.1 非破坏采样含水率的监测

在每个样地内，分别选取2种不同郁闭度样点进行采样，分别位于每个样地的林窗下（该林型郁闭度最低处）和林荫下（该林型郁闭度最高处）。测量点选择在地表死可燃物分布较均匀处设置样筐，每个点分别挖取1个20 cm×20 cm小样方死可燃物，记录厚度，然后保持其自然状态，分别放入样筐中，再放回原位，保持可燃物的原始状态。使用5#塑料方筛（尺寸为：265 mm×205 mm×85 mm），用尼龙网（18目，1 mm）加衬在其底部及四壁，上方加盖粗眼尼龙网（8目，2.5 mm），并在盛装样品后使用尼龙扎绳固定，以防止新凋落的树木叶片进入到容器内，也避免容器内的样品因风或小型动物的活动而变化。样筐上挂上号牌，号牌上记录样地与样点编号，以免重复观测时发生混淆。使用塑料容器而没有使用金属容器的原因是金属容器长期处在潮湿环境中会发生锈变而影响质量。

每日14:00左右（前后误差不超过10 min），按同样的样地顺序称量每个样地中2个样筐的质量并记录，记作湿质量，尽量保证同一样地的称量时间一致。各样地称量时，小心取出容器，尽量不破坏容器中可燃物和周围可燃物的结构。为了便于在野外称量样品的质量，选用了便携式电子天平（美国双杰（G&G）生产的JJ600Y型），称量时使用预先制作的折叠板在地表水平展开，安置并校准天平后在板盒内进行称量，以排除风的干扰。

1.2.2 破坏性采样含水率的监测

距离非破坏性采样筐放置地较远处，每日14:00在各样地内选择10个采样点，无遮荫、林荫下内各取5点（无日照实验日在样地内随机选取10点），采用破坏性采样方法对地表死可燃物进行收集，主要包括枯枝、落叶和杂草等[20]。为了保证精度，首先保证一定的质量，因此每个点装取100 g左右（上下误差不超过5 g），称鲜质量并记录。每次采样完毕后在信封上做好详细标记（采样时间和采样林型），带回室内，开口放置于通风处，防止腐烂。

1.2.3 气象数据的采集

气象数据由塔河林业局气象站和盘古林场气象观测站获得，包括春季防火期5—7月、秋季防火期9—10月的逐日气象数据。采集的气象要素有：温度（T）、相对湿度（H）、降水量（R）和风速（W）。

1.3 数据分析

采用协方差分析比较同一林型下不同采样方法地表死可燃物含水率之间的差异，并作Duncan显著性差异检验；采用配对样本t检验比较不同对照的精度差异；利用线性回归方程拟合含水率与气象因子之间的关系。所有的数据均采用SPSS18.0进行统计分析，利用Sigmaplot12.5进行绘图。

1.3.1 可燃物含水率的计算

可燃物含水率公式为：

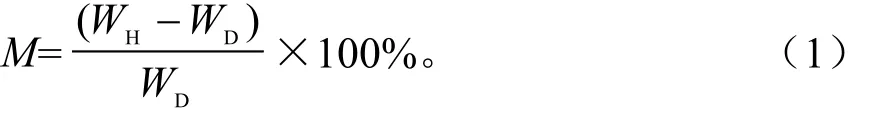
式（1）中：M为可燃物含水率（%）；WH为可燃物湿质量（g）；WD为可燃物干质量（g）。

其中，非破坏采样2个不同郁闭度含水率的算术平均值作为该样地当日14:00非破坏性采样方法的含水率值；破坏性采样10个点的含水率算术平均值作为该样地当日14:00破坏性采样方法的含水率值。

春季数据共30 d（组），秋季数据20 d（组）。

1.3.2 气象数据的处理

整理塔河林业局气象站和盘古林场气象站提供的气象数据：前n（n=1～5）天气象因子、n天前当日气象因子等，其中前n天气象因子和n天前当日气象因子以采样当日0点为基准。将前几天气象因子设为a，几天前当日气象因子设为b，均以下标表示，其后数字代表n值，如3天前当日平均温度记为Tb3，前2天平均相对湿度记为Ha2，前5天降水量之和记为Ra5，连旱天数记为D。

1.3.3 不同采样方法对模型精度的影响

根据Pearson相关性分析，确定对地表死可燃物含水率有显著影响的因子，剔除实验中的异常数据后，以每个样地的可燃物含水率或全部的含水率数据（以下简称“混合数据”）为因变量[21]，以气象要素（当天、前1天、前2天的温度、湿度、风速和降水量）为自变量，通过逐步回归方法建立多元线性方程[21]，具体形式为：

式（2）中：M为可燃物含水率（%）；Xi（i=1、2、…、n）为变量；Xi分别为当天、前1天、前2天的温度（℃）、湿度（%）、风速（m·s-1）、降水量（mm）等；bi为待估计参数。采用混合数据建模的目的是确定该方法能否提高模型精度。

采用n-Fold交叉验证法[22]计算模型精度[23]。对于某个样地的n个含水率数据，用n-1个含水率和气象要素进行逐步回归，建立多元线性模型，然后用剩余的一个数据验证，计算误差，重复n次。计算平均误差[20]，对不同对照的误差进行显著性检验（配对t检验），显著性水平设定为α=0.05，误差按下列公式计算：

平均绝对误差（MAE）：

平均相对误差（MRE）：

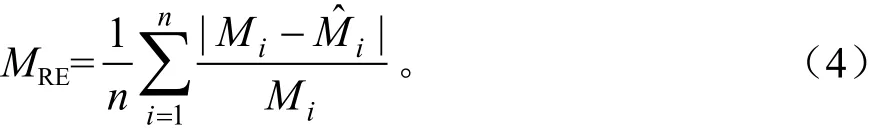
式（3）与（4）中：Mi为含水率实测值（%）；为可燃物含水率预测值（%）；n为样本数。

绘制利用不同数据建模进行比较分析的混合模型实测值与预测值的1∶1线，用以研究预测效果。

2 结果与分析

2.1 细小可燃物含水率与气象因子的相关关系

图1给出了3个林型非破坏性采样含水率和实验地不同距离的盘古和塔河气象站提供的有显著关系的气象因子之间的Pearson相关系数，结果表明，不同距离的气象因子与不同林型地表死可燃物含水率的影响因子相关性存在差异。利用盘古气象站数据构建的气象因子中前1天和前2天的降水量和Ran以及平均相对湿度Han（n=1～2）显著正相关，另外，春季和秋季分别与日最高温度Tmax和干旱天数D呈显著负相关，n（n=1～5）天前当日气象因子对可燃物含水率也有影响，但不如前三类因子。利用塔河气象站数据构建的气象因子中与地表死可燃物含水率相关性较强的都是与湿度相关的因子（Ha1和Ha2），温度和风速与含水率相关性较差。因此，在进行含水率预测时，只需采用湿度和降水量两个变量即可。

图1 含水率与气象因子相关性分析Fig.1 Correlation analysis between moisture contents and meteorological factors

2.2 不同采样方法下细小可燃物含水率预测模型的构建

通过多元线性逐步回归方法，筛选出2种采样方法构建的地表死可燃物含水率预测模型所采用的预测因子以及模型参数（见表2至表3），对于非破坏性采样含水率预测模型，当日降水量和R、前1天降水量和Ra1以及前2天平均相对湿度Ha2是影响其含水率变化最重要的因子；对于破坏性采样含水率预测模型，影响因子增加了前1天平均相对湿度Ha1和前2天降水量和Ra2，破坏性采样模型比非破坏性含水率进入模型的气象因子更多。

由表4可知，采用非破坏性采样方法建模的8个含水率系列的平均绝对误差为9.4%，平均相对误差为42.0%；而破坏性采样方法建模的平均绝对误差和相对误差分别为14.7%和58.3%。非破坏性采样法的平均绝对误差和相对误差都略小于破坏性采样。此外，全部数据混合建模比单独建模的平均误差有所增加，并没有改善模型的精度。主要原因是不同采样法下不同采样地的含水率不同，增加了含水率的变化幅度，导致模型精度下降[20]。

表2 非破坏性采样含水率预测模型Table 2 The prediction model of non-destructive sampling moisture

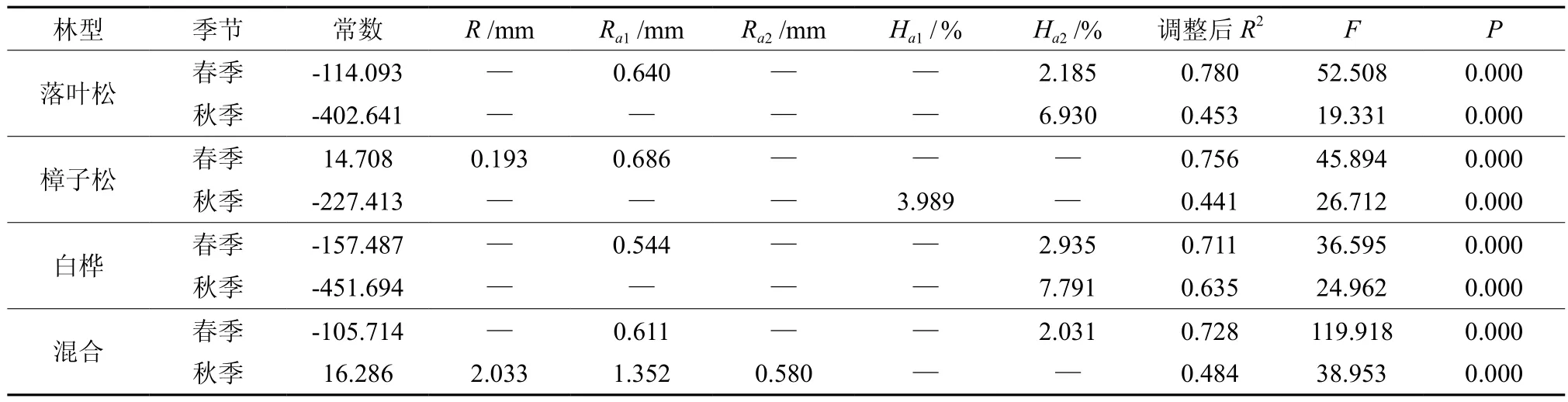
表3 破坏性采样含水率预测模型Table 3 The prediction model of destructive sampling moisture

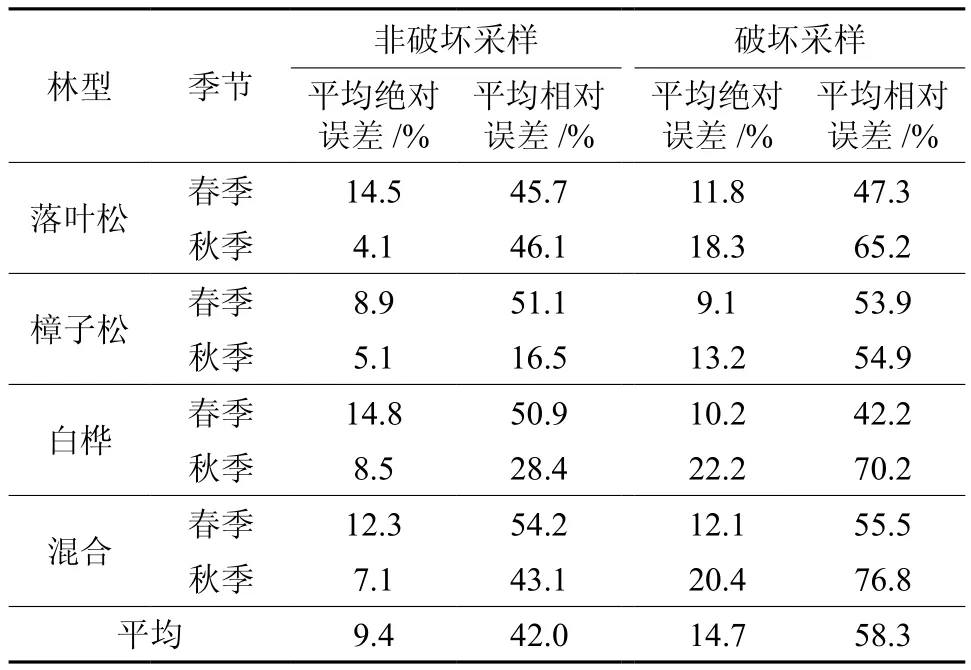
表4 2种采样方法建模的交叉验证误差Table 4 Errors of two types of sampling method models established using a cross validation method

2.3 不同采样方法细小可燃物含水率预测模型误差分析

结合图2可知，春季采用非破坏性采样含水率建模的4个系列中有3个系列的平均绝对误差大于破坏性采样，而秋季非破坏性采样的平均绝对误差全部小于破坏性采样；平均相对误差结果同平均绝对误差。对2种采样方法的2种误差的t检验结果表明，尽管春、秋季非破坏性采样和破坏性采样的平均绝对误差值各有优劣，但差异不显著（n=8，t=-1.873，P=0.103），平均相对误差同样差异不显著（n=8，t=-2.341，P=0.052）；对于春季2种采样方法的t检验的结果表明，平均绝对误差（n=4，t=1.621，P=0.203）和平均相对误差（n=4，t=0.281，P=0.797）差异都不显著，而秋季非破坏性采样的平均绝对误差（n=4，t=-8.678，P＜0.01）和平均相对误差（n=4，t= -6.649，P＜0.01）都极显著低于破坏性采样。这表明，在春季2种采样法差异不显著，预测效果相近，而在秋季使用非破坏采样较好。

总体来说，不同采样法所获得的含水率建模对模型预测的影响很大，非破坏性采样数据用于建模的预测效果更好。

由图3知，从不同模型的R2和样点分布情况以及各个模型的相关验证模拟线偏离1∶1线的程度，综合评价各模型对含水率的预测能力。春季，非破坏采样含水率值显然没有破坏性更加靠近1∶1线，相比较更加离散，实测含水率值高于100%数据较多，此部分实测值要高于预测值，预测偏低；而秋季非破坏性采样含水率普遍较低，且大多靠近1∶1线。破坏性采样含水率在有较大降水时，远高于非破坏性采样，这显然造成了误差增大，预测能力下降，整体预测偏低。

3 讨论

使用不同的采样方法对含水率预测模型的精度影响很大，春季3个林型使用破坏性采样方法的误差要略小于非破坏性方法，秋季使用非破坏性方法效果要好于破坏性方法。2种方法对于死可燃物影响的最大区别就是是否打破了自然状态下的可燃物密实度[21]，进而影响其内部空气流通以及水分蒸发的快慢。对于非破坏采样，在整个实验期内可燃物状态更加稳定，但实际上，在前期进行标准物制备的过程中，从某种程度上已经打破了其自然状态，而破坏性采样面临的问题是采样的标准以及采样点选取的问题，任何环节的错误都有可能造成其与真实值之间的背离，因此，在不同季节选取不同的采样方式对实验数据的准确性是至关重要的。

本文研究的春季破坏性采样收集的样品中大多为往年落地的松针、落叶和细小枝条，秋季样地主要是当年生长的新松针和叶片开始落至地面，进行破坏性采样时难免混入样品中，由于新落地的松针或叶片较往年落地的含水率偏高[19]，也可能加大了秋季破坏性采样含水率计算的误差。

图2 2种采样方法模型的误差对比Fig.2 Comparison of errors in the two sampling models

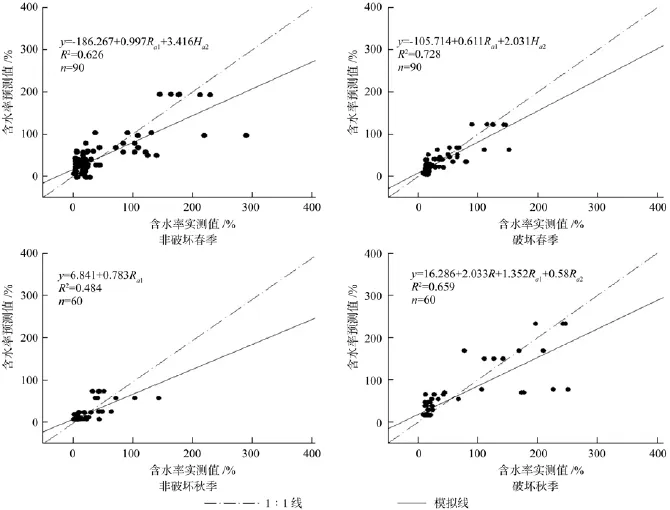
图3 不同采样法模型实测值与预测值的对比Fig.3 Comparison of measured and predictive value by different sampling methods

此外，野外采样方法对含水率测定值的影响很大，进而影响含水率预测模型的预测精度。确定合理的采样方式和采样间隔，对于减少误差尤其重要[24]。毛卫星等的研究表明，对于落叶松林下的地表死可燃物进行破坏性采样以采用间距2～8 m的采样距离为最佳，当采样强度为7个以上时，误差可达到10%以下[24]，这一研究对破坏性采样以及非破坏性采样间隔的探索具有很好的代表性，具体多大的采样间隔以及标准物设置的数量和位置能够使不同采样方式更接近获取地表死可燃物含水率的真实值，在今后的工作中应进一步研究。

本文只研究了一年中春、秋两季可燃物含水率变化的动态。与历史气象记录比较，本研究的气象条件属于中等条件，因此，所反映的可燃物含水率动态只是平均水平[26]。对于森林火灾而言，特别是重、特大森林火灾，往往在气象条件明显偏离历史平均水平的条件时发生，如温度偏高，且降雨量显著偏少等，这对采用不同采样方式进行含水率数据的获取无疑有较大的影响。因此，今后应进一步开展多种时间尺度的相关研究，以完善细小可燃物含水率预测模型的精度。

参考文献：

[1] 邸雪颖, 王宏良. 林火预测预报[M]. 哈尔滨: 东北林业大学出版社, 1993: 27.

[2] 王瑞军, 于建军, 郑春艳. 森林可燃物含水率预测及燃烧性等级划分[J]. 森林防火, 1997(2): 16-17.

[3] 金森, 李绪尧, 李有祥. 几种细小可燃物失水过程中含水率的变化规律[J]. 东北林业大学学报, 2000, 28(1): 35-38.

[4] 刘曦,金森. 基于平衡含水率的森林可燃物含水率预测方法的研究进展[J]. 林业科学, 2007, 43(12): 126-133.

[5] Weidman R H. Relation of weather forecasts to the prediction of dangerous forest fi re condition [J]. Monthly Weather Review,1923, 11: 563-564.

[6] GIsborne H T. Using weather forecasts for prediction forest fi re danger [J]. Monthly Weather Review, 1923,11:563-564.

[7] Ana Daria Ruiz González A C, Jose Antonio Vega Hidalgo B,Juan Gabriel Alvarez Gonzalez A. Construction of empirical models for predictingPinusspp. dead fine fuel moisture in NW Spain. I: Response to changes in temperature and relative humidity[J]. International Journal of Wildland Fire, 2007, 18:71-83.

[8] Stuart Matthews A, Jim Gould A, Lachie McCaw. Simple models for predicting dead fuel moisture in eucalyptus forests[J].International Journal of Wildland Fire, 2010, 19:459-467.

[9] 杜秀文, 李茹秀, 王英杰. 几种森林类型可燃物含水率与气象因子关系的分析[J]. 东北林业大学学报, 1988, 16(3): 87-90.

[10] 居恩德. 可燃物含水率与气象要素相关性的研究[J]. 森林防火, 1993(1): 17-21.

[11] 张国防, 林文革, 花昆福, 等. 杉木人工林地表易燃物含水率变化规律[J]. 福建林学院学报, 2000, 20(1): 77-79.

[12] 覃先林, 张子辉, 易浩若, 等. 一种预测森林可燃物含水率的方法[J]. 火灾科学, 2001, 10(3): 37-40.

[13] 曲智林, 吴娟, 闵盈. 具有时滞的可燃物含水率预测模型[J]. 东北林业大学学报, 2012, 40(3): 120-122.

[14] 王栋. 森林可燃物含水率与森林火灾危险性的研究[J]. 林业科学研究, 1992, 5(3) : 549-553.

[15] 张运林, 张恒, 金森, 等. 季节和降雨对细小可燃物含水率预测模型精度的影响[J].中南林业科技大学学报,2015,35(8):5-12.

[16] 张思玉, 蔡金榜, 陈细目. 杉木幼林地表可燃物含水率对主要火环境因子的响应模型[J]. 浙江科学学报,2006,23(4):439-444.

[17] 张光英, 高永刚, 曹晓波, 等. 伊春市五营森林可燃物含水率预测模型初步研究[J]. 安徽农业科学,2007,35(36):11956-11958.

[18] 高永刚, 张广英, 顾红, 等. 森林可燃物含水率气象预测模型在森林火险预报中的应用[J]. 中国农学通报,2008,24(9):181-185.

[19] 陈鹏宇. 帽儿山林场地表死可燃物含水率直接估计法的误差分析[D]. 哈尔滨:东北林业大学, 2011: 32.

[20] 王家华, 高海余. 利用循环交叉验证法确定变异函数[J]. 西安石油学院学报, 1992, 7(4): 3-9.