基于CFD方法的舵角对有效功率的影响
2018-04-20薛振宇陈霞萍任海奎
薛振宇, 陈霞萍, 任海奎
(上海船舶运输科学研究所 航运技术与安全国家重点实验室,上海 200135)
0 引 言
温室气体是引起全球气候变暖的一大因素,对全球的生态环境、经济环境及人类的未来均有不利的影响。近年来,国际海事组织(International Maritime Organization, IMO)出台了《新船能效设计指数(Energy Efficiency Design Index, EEDI)计算方法临时指南》,EEDI指数的设立旨在衡量船舶设计和建造能效水平,为新造船舶建立最低的能源效率标准。为规范试航阶段EEDI指数的评估流程,IMO发布《船舶和海上技术通过分析测速试航数据以确定速度和功率性能的评估导则》(ISO 15016—2015),其中,规定船舶试航时的舵角需在±5°的范围内,舵角对功率的影响可予以忽略。然而,在船舶实际营运航行中,船舶受到复杂的外界因素影响会发生偏航,通常需依靠一定的舵角以保持航向的稳定性,其舵角常会超过±5°的范围。由于转舵会增加船舶阻力,降低推进效率,对船舶的航速和功率将产生影响。所以,在船舶的实际营运中,舵角对船舶功率的影响是不可忽略的。
研究舵角对船舶功率的影响,需研究船-桨-舵相互干扰的问题。早期,相关的研究主要依靠物理模型试验进行分析研究。近年来,随着技术的发展,采用计算流体动力学(Computational Fluid Dynamics, CFD)方法来研究船-桨-舵相互干扰问题,杨春蕾[1]、吴召华[2]、杜云龙[3]、祝启波[4]等采用CFD方法,开展了关于船-桨-舵相互干扰问题的研究工作,对船体尾流场的变化、桨和舵的几何参数、位置布置及数值模拟精度等相关计算结果进行了分析,得出了一些有益的结论。
在船舶快速性的研究中,通常是开展对船型和螺旋桨的研究,带舵的情况下,舵角通常设置为0°;而对操舵的研究一般聚焦在船舶操纵性领域中,通常为大舵角(10°~35°)操舵,在有舵角的情况下,对船舶快速性的影响研究较少。但在营运船舶的实际航行过程中,舵角的范围通常在±10°的范围中,此时,船舶能效水平的评估需考虑舵角对船舶功率的影响。
本文以一艘开展实船营运性能监测研究的集装箱船作为研究对象,研究在实船营运的常用舵角范围内,舵角变化对船舶阻力和船舶有效功率的影响。
1 数值方法
1.1 控制方程
在工程应用中,通常使用雷诺平均法求解N-S方程,把速度和压力等物理量分解为平均量和脉动量,同时加上湍流模型,对RANS方程进行封闭。这里利用商用软件STAR-CCM+进行数值计算,采用三维隐式不定常求解器,选择欧拉多相流模型,使用Realizablek-ε对N-S方程进行封闭,壁面函数采用2层所有Y+壁面处理。
1.2 VOF模型
Volume of Fraction(VOF)模型是一种捕捉界面的方法,用于处理自由液面问题,该模型可有效处理复杂的几何体和碎波的影响。在多相流中,VOF模型使用C函数,该函数是关于时间和位置的函数,在液面的单元网格上,定义C函数是该时刻流体所占的空间与网格空间的比例,以此确定自由面的位置和形状,C函数的值在0~1间浮动,0代表网格空间中不含流体,1代表网格空间中充满流体,VOF方程为
(1)
采用VOF方法对自由液面进行捕捉,同时创建静水VOF波模型,软件自动生成速度场函数、压力场函数和体积场函数,并应用至速度入口和压力出口。
2 计算模型建立
2.1 计算对象
选用某万箱船及扭曲舵作为研究对象,船及舵模型见图1。实船参数见表1,计算工况见表2,数值计算的模型尺度及水温参数均与物理模型试验参数相同。


图1 船、舵模型

表2 船模数值计算工况
2.2 网格划分
考虑到舵的型式为扭曲舵,左右不对称,此处选取整船进行数值计算。计算域为一长方体控制域(见图2),坐标系原点位于船舶艉部,零号站与基线的交汇处,x轴正向指向船舶艏部,y轴正向指向船舶左舷,y=0表示船舶的中纵剖面,z轴按右手系法则定向,沿型深垂直向上。计算域入口距船首的距离为L(L为垂线间长),计算域出口距船尾的距离为4L,平行于船舶中纵剖面的两侧距中纵剖面的距离为1.5L,计算域底部距基线面的距离为L,计算域顶部距基线面的距离为0.5L。
对船舶模型表面进行包面处理,对图2中的长方体域和船舶模型进行布尔运算,获得封闭的空间,在表面重构的基础上,对网格进行划分。网格采用切割体网格和棱柱层网格,为加快运算速度和充分利用计算机的资源,保证运算精度和运算效率,需对不同区域的网格进行不同程度的加密,即越接近船体的空间越充分加密网格,而越远离船体的的空间越充分稀疏网格,同时考虑到船首、船尾及舵的几何曲率较大,需对这些区域进行层层加密。同时,考虑到自由表面的影响,需对垂直液面方向的空间进行网格加密。按上述方法进行网格划分(见图3),计算域网格划分数量约为317万。
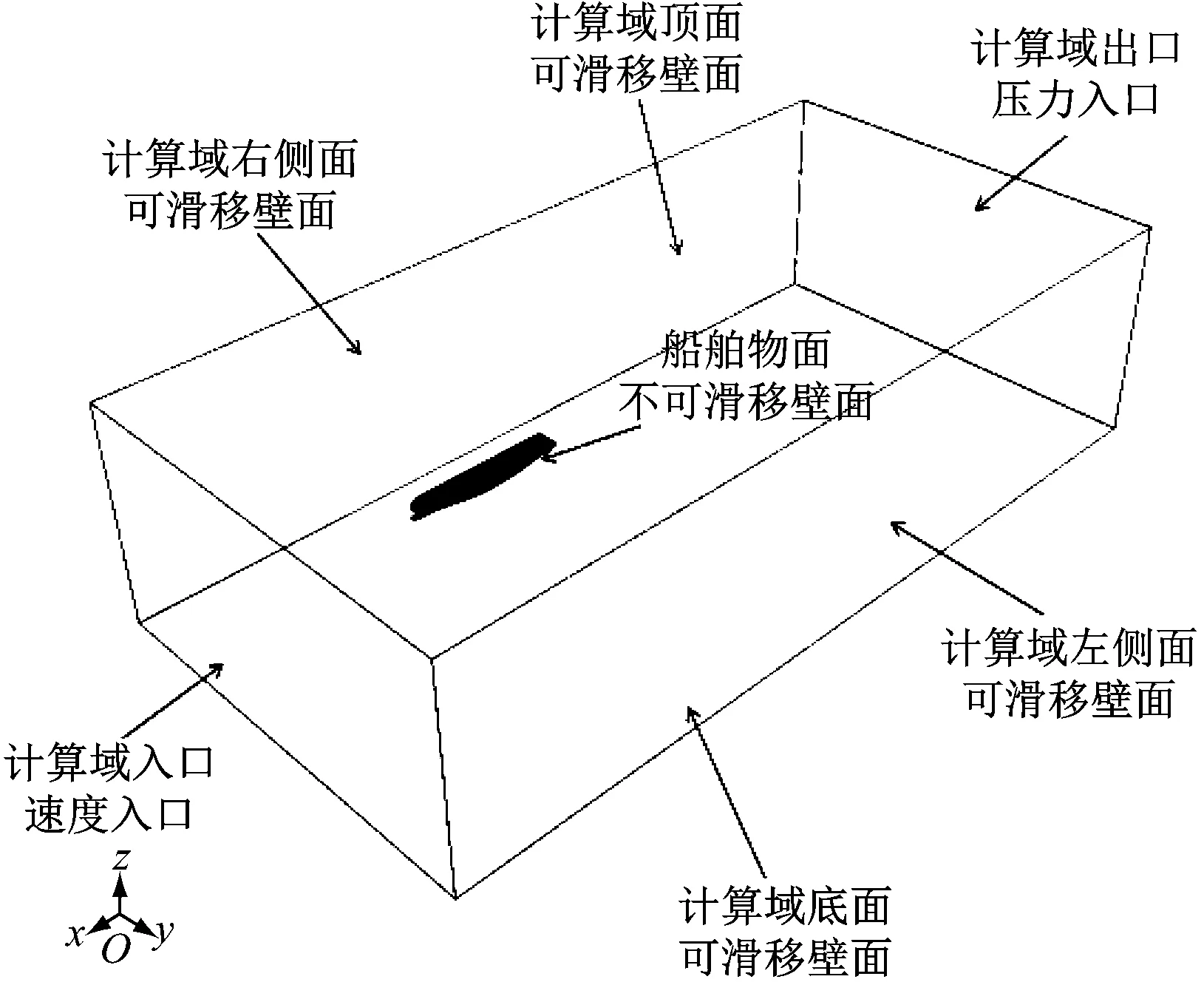
图2 计算域

图3 计算域网格
2.3 边界条件设置
计算域的边界条件设置如下:
(1) 船体及舵的壁面设置为不可滑移壁面。
(2) 计算域进口设置为速度入口。
(3) 计算域出口设置为压力出口。
(4) 计算域底部、顶部和两侧设置为可滑移壁面。
3 数值计算结果与分析
3.1 数值方法可靠性验证
为验证数值计算方法的可靠性,需对常规工况0°舵角船舶静水阻力数值进行计算,对试验结果与计算结果进行比较,当两者误差在合理的范围内,可认为数值计算方法是可靠的。模型试验由上海船舶运输科学研究所完成,模型试验的速度范围较大,对应的实船航速为16~24 kn,共有9个速度点,为保证计算方法对所有速度点均有良好的适应性,所以在CFD计算中,速度点的选取与试验速度保持一致。

图4 0°舵角船模总阻力计算值与试验值
数值计算结果与模型实验结果对比见图4,该船的数值计算结果与模型试验结果比较接近,误差范围为-0.21%~1.62%,精度可满足工程要求,采用该数值计算方法用于计算和分析船舶阻力性能是可行的。
3.2 变舵角工况有效功率计算结果
在验证数值计算方法可靠性的基础上,对变舵角工况下船舶静水阻力及有效功率进行数值计算工作。
根据实船营运统计数据显示,船舶实际航速主要分布在16~24 kn。在实船营运中,为保持航向,舵角θ通常在±10°的范围内,因此考虑计算工况为计算航速Vs为16 kn,20 kn,24 kn,计算舵角θ为±2.5°,±5°,±7.5°,±10°,即计算工况包含3个速度和8个舵角,共24个计算工况,通过计算分析不同航速、不同舵角下船舶有效功率的变化规律。舵角正负规定为从z轴由正向负观察,顺时针转舵为右转舵,逆时针转舵为左转舵。
将不同航速及不同舵角下数值计算得到的船模阻力,换算至实船有效功率,不同舵角下船舶有效功率-速度曲线见图5和图6。

图5 右舵下实船有效功率计算值

图6 左舵下实船有效功率计算值
不同舵角对船舶有效功率的影响见表3和图7。由图7可知,当舵角在±5°的范围内,对船舶有效功率的影响约为1%,相对较小;当舵角在±7.5°时,对船舶有效功率的影响约为2%;当舵角在±10°时,对船舶有效功率的影响在3%~4%,由于舵型为扭曲舵,对于2个相同大小的舵角,左舵对船舶有效功率的影响高于右舵。由计算结果可见舵角在-10°~-7.5°及7.5°~10°的区间中,对船舶有效功率的影响是较为明显的,说明在船舶营运的过程中,舵角的影响不能忽略不计。
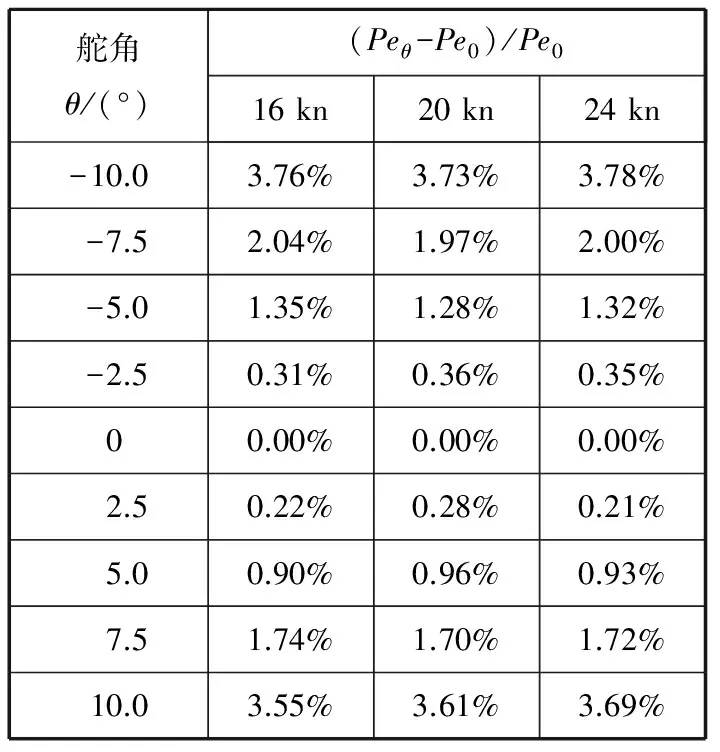
表3 不同舵角对实船有效功率的影响

图7 不同舵角对实船有效功率的影响
3.3 变舵角工况流场分析
根据变舵角工况的数值计算结果,选取正向舵角(右舵)进行流场分析。0°舵角和10°舵角的压力分布云图见图8,可以观察到舵角的变化对船体表面压力分布的影响较小,可忽略不计。舵角的改变导致舵的表面压力发生变化,取舵角分别为0°,5°,10°,分析其表面压力分布。

a) 0°舵角船舶艉表面压力

b) 10°舵角船舶艉表面压力
不同舵角下的扭曲舵的背面(负y轴)和正面(正y轴)的压力分布云图见图9和图10,舵由两部分舵叶构成,上部分是和船体连接固定不动的舵叶,下部分是可变换舵角的舵叶。从图9和图10中分析,变化舵角对固定的舵叶的压力分布的影响较小,而对可旋转的舵叶上的压力分布影响较大,说明转舵导致功率增加的因素主要来源于可旋转的舵叶本身。
由云图可知,可旋转舵叶的下部区域的背面分布着负压,正面分布着正压,随着舵角的增加,正面区域的正压部分改变相对较小,而负面区域的负压部分改变相对较大,所以舵角发生变化后,对扭曲舵上的压力影响主要来源于负压,发生的区域在可旋转舵叶的下部区域,可见由于转舵产生压阻力导致船舶有效功率的增加。

a) 0°舵角下扭曲舵背面压力分布

b) 5°舵角下扭曲舵背面压力分布
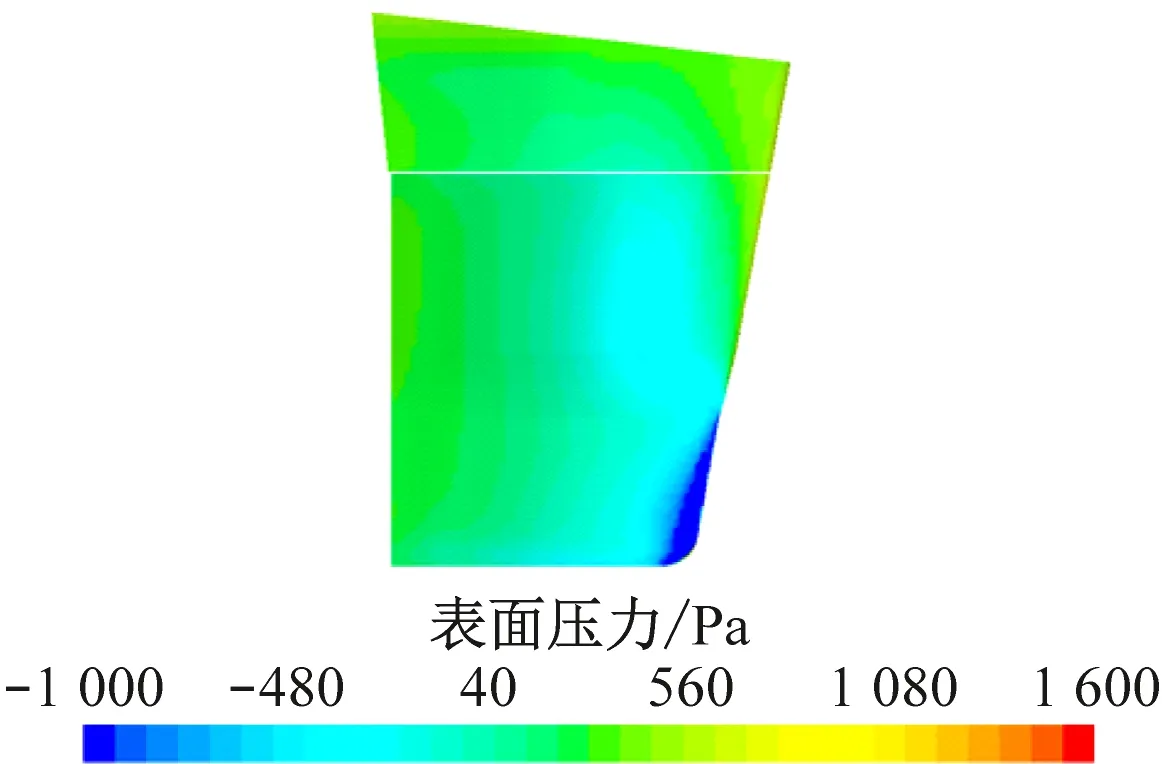
c) 10°舵角下扭曲舵背面压力分布

a) 0°舵角下扭曲舵背面压力分布

b) 5°舵角下扭曲舵背面压力分布

c) 10°舵角下扭曲舵背面压力分布
4 结 语
航行中转舵角对船舶艉部流场产生影响,增加船舶阻力,随着舵角增加,船舶有效功率也随之增加。当舵角在<5°的范围内,对船舶有效功率的影响相对较小,影响可忽略;当舵角为±7.5°时,船舶有效功率约增加2%,在舵角达到±10°时,船舶有效功率约增加3%~4%,此时舵角对船舶能效的影响不能被忽视。
本文只考虑舵角对阻力的影响,还未考虑舵角对推进效率的影响,事实上转舵角后艉部流场发生变化,推进因子也会发生变化,转舵角对船舶推进功率和收到功率的影响在后面的工作中还需做更深入的研究。
参考文献:
[1]杨春蕾,朱仁传,缪国平,等. 基于CFD方法的船/桨/舵干扰数值模拟[J]. 水动力学研究与进展A辑,2011,26(6):667-673.
[2]吴召华. 基于体积力法的船/桨/舵粘性流场的数值研究[D].上海:上海交通大学,2013.
[3]杜云龙.船桨耦合数值计算研究[D].上海:上海船舶运输科学研究所,2012.
[4]祝启波. 基于船-桨-舵全耦合求解的船舶自航性能数值预报方法研究[D].镇江:江苏科技大学,2016.
