威胁联网环境下的无人机突防路径决策

张辉明，　鲁　艺，　朱　杰

(空军工程大学航空航天工程学院，西安　710038)

0　引言

无人机在执行低空突防任务前必须为其规划出安全可飞的飞行航迹以提高其作战效率和生存概率。目前无人机航迹规划研究主要集中在威胁规避式的突防航迹规划[1-6]，旨在为无人机寻找一条最优或者较优的航迹。而在实际突防过程中，各个威胁单元之间时刻都在进行着信息交流和资源共享，协同完成整个覆盖范围内的任务，称之为威胁联网[7]。文献[7]较早提出了威胁联网的概念，建立了威胁相互支援信息表，但威胁相互支援表主要是根据各方面专家的意见和决策者的经验给出，主观性较强。文献[8]利用威胁相互

支援表进行了航迹规划，但其本质上仍然是威胁联网条件下的航迹重规划问题。文献[9]在威胁联网模型中引入目标指示概率，但其默认当前威胁向所有联网威胁传递信息,且目标指示概率为威胁之间距离的函数，不符合战场实际。

为使无人机在威胁联网的环境中顺利完成突防任务，不能只依赖于地面站的离线规划航迹，必须具备一定的自主路径决策能力。动态贝叶斯网络在时序过程中对不确定性问题建模具有很大优势，在此基础上进行的路径决策更具有合理性，可以保持决策结果的鲁棒性[10-12]。路径决策问题实际上是一个定性决策问题，因此离散动态贝叶斯网络适合解决此类问题。本文通过变结构离散动态贝叶斯网络构建无人机突防路径自主决策模型，采用此模型完成了无人机在威胁联网环境下的一系列突防路径自主决策。

1　SVDDBN推理机制

1.1　SVDDBN描述

本文以SVDDBN为基础，设计无人机在威胁联网环境下的突防路径自主决策模型，以适应动态变化的环境。

如果组成一个离散动态贝叶斯网络的结构或参数在不同时间片下发生变化，则这类离散动态贝叶斯网络称为变结构离散动态贝叶斯网络[13]，如图1所示。

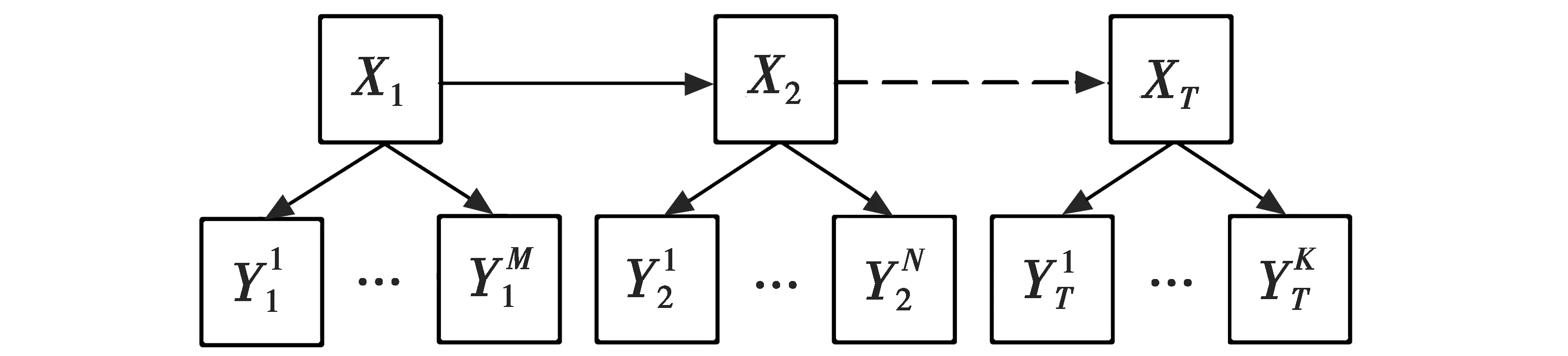
图1　SVDDBN示意图Fig.1　The sketch map of SVDDBN

实际应用中，随着时间片的推移，模型变化主要体现在决策变量的个数和观测变量的个数上。可以根据实际获得的观测变量个数和状态，获得决策变量的个数和状态，并根据预先建立的参数库，获得SVDDBN决策模型和可变的参数。如果待决策的变量发生变化，则可能是新的决策推理过程的开始。如果决策者的偏好发生变化，而环境并无变化，则必将引起条件概率表的变化。同样可以根据偏好的变化从预先建立的参数库获得可变的参数。

1.2　SVDDBN推理算法

对于一个共有T个时间片的SVDDBN，每一个时间片对应的SVDDBN的结构为BNTi(i=1,…,T)，对应的条件概率表为intraCPTi(i=1,…,T)；具有ni个决策节点和mi个观测节点，分别记为Xij(i=1,…,T;j=1,…,ni)和Yij(i=1,…,T;j=1,…,mi)，下标i为变量所在时间片，下标j为变量在决策变量集合或观测变量集合中的序号。前后两个时间片间的条件概率表为interCPTi(i=1,…,T-1)，对这个SVDDBN进行推理，本质上就是计算所有的观测变量处于某一个观测状态下决策节点的联合分布，即计算P(X11,…,X1n1,…,XT1,…,XTnT|Y11,…,Y1m1,…,YT1,…,YTmT)。其中，XTi和YTj分别表示时间片T中的第i个决策变量和第j个观测变量。

贝叶斯网络的基础是条件概率方程和条件独立假设。条件概率方程为

(1)

条件独立假设为

(2)

式中：X={X1,…,Xn}表示贝叶斯网络中的所有变量；P(X)表示X的联合概率分布；Pa(Xi)表示节点Xi的父节点；P(Xi|Pa(Xi))表示条件概率。

SVDDBN仍然是一个表示变量之间依赖关系的有向无环图，同样遵循静态贝叶斯网络的条件独立假设和D-分离特性。

由贝叶斯网络的条件独立性可知，所有变量的联合概率分布等于所有条件概率的乘积。因此有

P(X11,…,X1n1,…,XT1,…,XTnT,Y11,…,Y1m1,…,YT1,…,

(3)

式中：i=1,…,T；j=1,…,mi；k=1,…,T；l=1,…,nk。因此有

(4)

式中:i，j，k，l都是整数;X11,…,X1n1,…,XT1,…,XTnT代表决策变量的某一个组合状态，其组合状态的数目等于所有决策变量状态数的乘积;Y11,…,Y1m1,…,YT1,…,YTmT是观测变量的组合状态，分子是该观测变量和决策变量处于某一组合状态的联合分布，分母是该观测变量和决策变量所有组合状态的联合分布的加和。

2　基于SVDDBN的突防路径决策模型

2.1　突防任务描述

无人机在威胁联网的环境下，需要完成联网后的威胁状态评估和无人机的突防路径自主决策。图2是无人机的突防可参考路径，具体的威胁评估和突防路径决策实现过程如下。

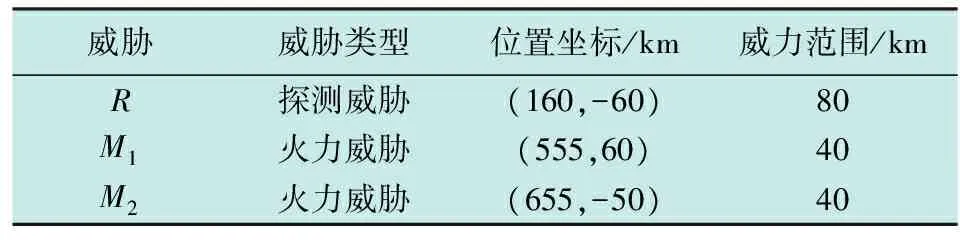
1) 无人机需从起点S到目标点T完成突防任务，在执行突防任务前，需对该战场区域进行预先侦察，获得该区域各类威胁目标的位置和范围等。为描述问题方便，本文仅考虑预警雷达和防空导弹，且探测威胁可以穿越，火力威胁不可穿越。经侦察，该区域存在的敌方威胁包括探测威胁R，火力威胁M1和M2。

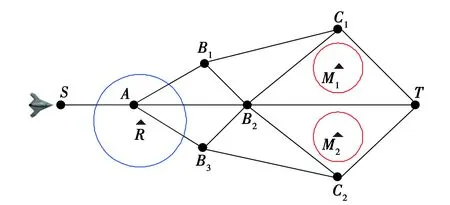
图2　无人机突防可参考路径Fig.2　Referable paths for UAV’s penetration

2) 敌方预警雷达的探测范围往往非常大。假设由于地形和禁飞区的影响，很难找到敌方的探测盲区进行突防，因此无人机必须穿越探测威胁R，探测威胁R将以一定的概率发现无人机并对其进行跟踪，当无人机飞离探测威胁时，探测威胁R会将无人机的速度和方向信息传递给后方的火力威胁M1和M2，使其由正常状态转为战备值班状态，以增大对无人机的拦截概率。

3) 敌方指挥机构会根据探测威胁提供的目标信息，通过调整防空导弹的目标航路，对无人机进行拦截。因此，无人机在穿越探测威胁时，不同的机动方式将会导致后方的火力威胁不同的响应。

4) 当无人机在航迹点A飞向航迹点B1时，火力威胁M1的目标航路捷径较小，而火力威胁M2的目标航路捷径较大，因此火力威胁M1联网，其威胁扩大。同理，当无人机在航迹点A飞向航迹点B3时，火力威胁M2联网，其威胁扩大。当无人机由航迹点A飞向航迹点B2时，火力威胁M1和M2的目标航路捷径均较小，因此火力威胁M1，M2均联网。

用变结构离散动态贝叶斯网络对突防路径问题进行决策，需要多级动态贝叶斯网络[14-15]。

在图2所示的突防路径决策问题中，第一级有3个选择，第二级有9个选择。第一级决策选择A-B1，A-B2，A-B3。第二级决策选择B1-C1-T，B1-B2-T，B1-B2-C2-T，B2-C1-T，B2-T，B2-C2-T，B3-B2-C1-T，B3-B2-T，B3-C2-T。为了方便，将上述各个航迹段分别定义为p1-1，p1-2，p1-3和p2-1，p2-2，p2-3，p2-4，p2-5，p2-6，p2-7，p2-8，p2-9。pi-j中的i表示第i级决策考虑的航迹，j表示该级的第j个航迹段。

2.2　路径决策模型

从广义上讲，决策节点为父节点，观测节点为子节点，而且必然在父节点的状态中，有一个状态与子节点直接相关。在对无人机的飞行航迹pi-j进行决策时，需要对航迹长度Lpi-j和威胁等级Wpi-j进行综合考虑，以选择最佳的突防路径。

假定有n条决策路径，每条路径都要考虑其路径长度和威胁等级2个因素，因此决策节点有n个，观测节点有2n个，分别反映n条路径的长度和威胁。在上述的突防路径决策问题中，第一级时间片中共有3条决策路径，则观测节点有6个，第二级时间片中共有9条决策路径，则观测节点有18个。

为了定量反映路径的长度和威胁等级，本文采用序数等级法，即根据这样一个原则，第一级时间片中有3条决策路径，将路径长度由近到远分别赋值1，2，3，则观测节点Lp1-j的观测值lp1-j有3个状态，即lp1-j∈{1,2,3}，将威胁等级由小到大也分别赋值1，2，3，则观测节点Wp1-j的观测值wp1-j有3个状态，即wp1-j∈{1,2,3}，该威胁等级由路径位于探测威胁中的长度大小而定。第二级时间片中共有9条决策路径，将路径长度由近到远分别赋值1～9，则观测节点Lp2-j的观测值lp2-j有9个状态，即lp2-j∈{1,2,…,9}。该时间片内决策路径的威胁等级可以分为4个等级。若路径周围仅有一个未联网的火力威胁，威胁等级最小，赋值为1；若路径周围仅有一个联网的火力威胁，威胁等级中等，赋值为2；若路径周围有一个未联网的威胁和一个联网后的威胁，威胁等级较高，赋值为3；若路径周围有两个联网后的火力威胁，威胁等级最高，赋值为4，则观测节点Wp2-j的观测值wp2-j有4个状态，即wp2-j∈{1,2,3,4}。于是可以建立如图3所示的基于SVDDBN的突防路径决策模型。

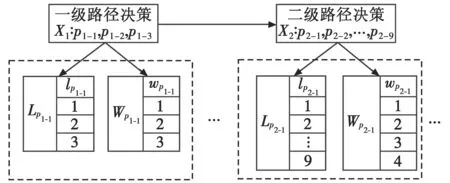
图3　基于SVDDBN的路径决策模型

3　SVDDBN自适应参数产生算法

已知决策节点的某一个状态，可以发现其相关节点总有一个最优状态，也总有一个最差状态。如果将该相关节点的状态按一定顺序排列，则最优状态和最差状态必然分布在两端。例如选择路径pi-j，路径pi-j的长度最短是其最优的，而路径pi-j的长度最长是其最差的。

以第二级路径决策节点为例，其有9个状态(p2-1,p2-2,…,p2-9)，观测节点Lp2-j的观测值lp2-j有9个状态，观测节点Wp2-j的观测值wp2-j有4个状态，条件概率表就是确定P(Lp2-j=lp2-j|p2-j)和P(Wp2-j=wp2-j|p2-j)，其中，j=1,2,…,9，lp2-j∈{1,2,…,9}，wp2-j∈{1,2,3,4}。

首先确定节点Lp2-j在j=1时的条件概率表，即P(Lp2-1|p2-1)，此时决策节点的状态p2-1与观测节点Lp2-1相关，而且Lp2-1的状态是从小到大排列。因此必然应该是P(Lp2-1=1|p2-1)>P(Lp2-1=2|p2-1)>…>P(Lp2-1=9|p2-1)，此时可以构成条件概率表，即

(5)

式中：lp2-1∈{1,2,…,9}；α∈{1,2,…,n}，α的取值可按照该决策节点的重要性，与决策者的偏好有关。

然后确定节点Wp2-j在j=1时的条件概率表，即P(Wp2-1|p2-1),此时决策节点的状态p2-1与观测节点Wp2-1相关，而且Wp2-1状态是从小到大排列。因此必然应该是P(Wp2-1=1|p2-1)>P(Wp2-1=2|p2-1)>…>P(Wp2-1=4|p2-1),此时可以构成条件概率表,即

(6)

式中:wp2-1∈{1,2,3,4};β的取值方式与式(5)中的α相同。

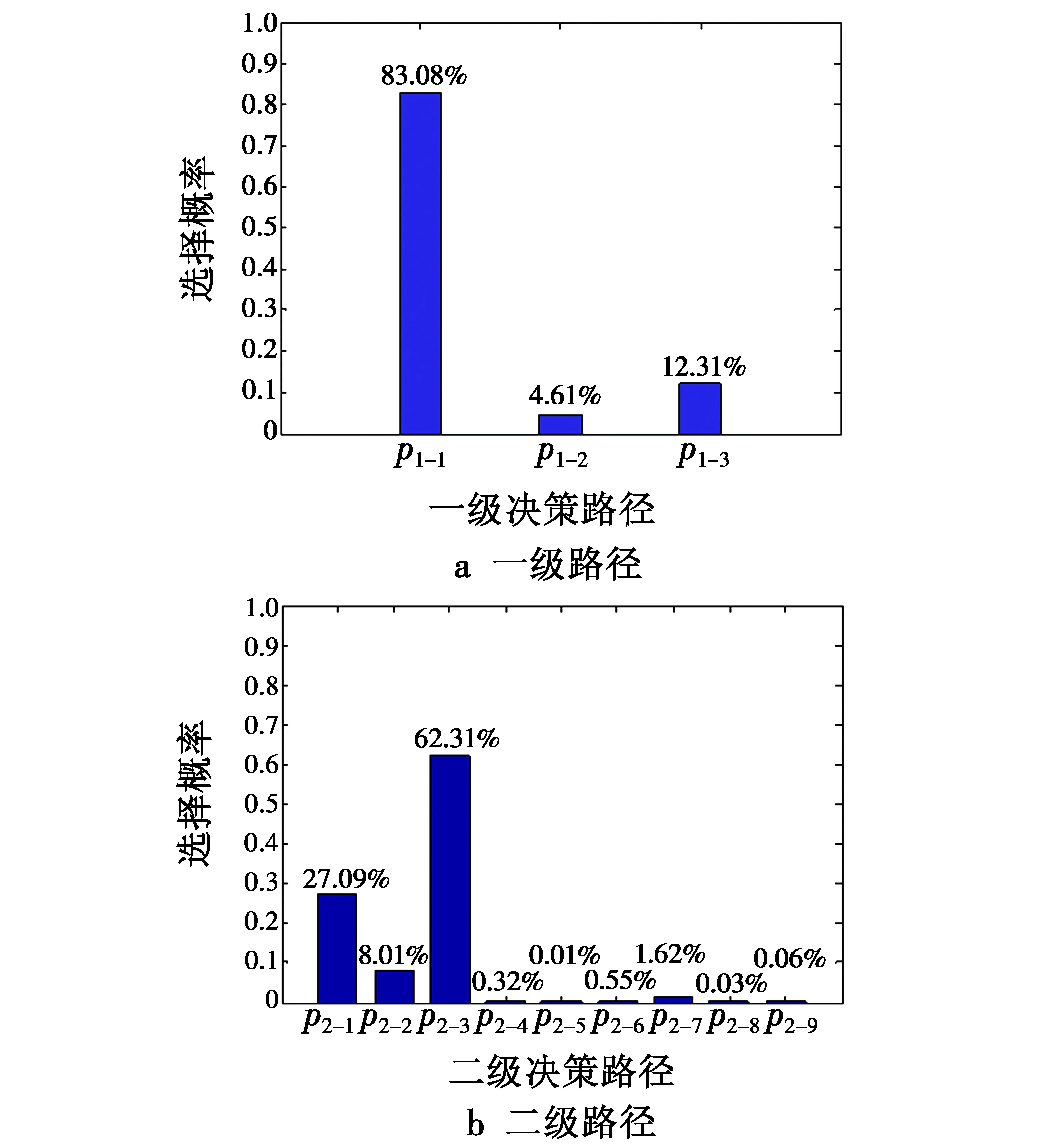
而对于决策节点的状态p2-1，Lp2-j和Wp2-j(j=2,…,9)都是与其不相关的节点，但是也存在一定的偏好，因为如果选择航迹p2-1，而此时航迹p2-2长度最近，威胁等级又最低的概率都应该是小的，否则就不可能选择航迹p2-1，这正好与相关节点是相反的概率分布。因此有P(Lp2-2=1|p2-1)

(7)

式中:j=2,…,9;lp2-j∈{1,2,…,9};wp2-j∈{1,2,3,4}。

其他决策节点和观测节点都如此处理，就可以自动生成符合要求的条件概率表。

4　仿真实验与分析

某无人机执行一项低空突防任务，起始点为S，目标点为T。经预先侦察获知作战区域内威胁分布如表1所示。

表1　威胁分布表

假设由于地形和禁飞区的影响，无人机必须穿越探测威胁R，在执行任务前为无人机规划出的可参考航迹点如图4所示。

图4　可参考航迹示意图

图4中的各个航迹点的坐标如表2所示。通过计算可以得到航迹pi-j的实际长度L、观测节点Lpi-j,Wpi-j的值，结果如表3所示。

根据3节的自适应参数产生算法，可以得出该突防路径决策模型的条件概率表。式(5)中的α取1，式(6)中的β取2，反映了决策者更偏好于威胁较小的路径。前后两个时间片之间的条件概率则是反映前一个时刻的决策对下一个时刻的决策的影响，如表4所示。

表2　航迹点坐标

表3　航迹相关参数值

表4　时间片间条件概率表

无人机在穿越探测威胁时，在A点被探测威胁发现，由于威胁联网的影响，无人机需做一定的机动决策，以快速通过该区域，决策结果如图5a所示。无人机穿出探测威胁后，需要对后方的火力威胁进行规避，突防路径决策结果如图5b所示。

图5　突防路径决策结果Fig.5　The result of decision-making for penetration path

从以上结果可以看出，无人机在被探测威胁发现后，会做一定的机动决策，尽快穿出探测威胁，因此选择路径p1-1,即图4中的A-B1。在威胁联网的情况下，无人机选择路径p1-1后，由于火力威胁M2的目标航路捷径较火力威胁M1的目标航路捷径大得多，所以火力威胁M1联网，而火力威胁M2未联网，因此选择路径p2-3进行突防，即图4中的B1-B2-C2-T，以避开对无人机杀伤概率较大的火力威胁M1，而从火力威胁M2的一侧进行突防，以提高无人机的生存概率。

5　结束语

威胁联网环境下的无人机突防航迹规划是近年来的研究热点与难点。无人机穿越探测威胁的路径不同会导致后方的火力威胁的响应不同，基于SVDDBN的决策模型与传统的DDBN决策模型相比，克服了限定在各个时间片的静态网络结构和参数完全相同的假设条件下无法对不确定问题进行建模的缺点，可以较好地适应节点状态数、观测变量个数等的突然变化，综合战场所有可观测信息加以推理，从而得到符合当前态

势的路径决策结果。

[1]SAMAR R,REHAMAN A.Autonomous terrain-following for unmanned air vehicles[J].Mechatronics,2011,21(5):844-860.

[2]李璠,郝应光.基于改进混沌遗传算法的无人机航迹规划[J].电光与控制,2012,19(8):15-19.

[3]吴天爱,吴云玉,别晓峰.采用病毒粒子群优化算法的飞行器航迹规划[J].电光与控制,2014,21(8):102-105，109.

[4]LUGO-CARDENAS,FLORES G,SALAZAR S,et al.Dubins path generation for a fixed wing UAV[C]//International Conference on Unmanned Aircraft Systems(ICUAS)，Piscataway,NJ:IEEE Press,2014:339-346.

[5]YAO P,WANG H L,SU Z K.UAV feasible path planning based on disturbed fluid and trajectory propagation[J].Chinese Journal of Aeronautics,2015,28(4):1163-1177.

[6]何仁珂,魏瑞轩,张启瑞,等.基于拟态电势能的飞行器航路规划方法[J].北京航空航天大学学报,2016,42(7):1543-1549.

[7]符小卫,高晓光,何建华.威胁联网下的飞行路径规划[J].飞行力学,2003,21(3):67-69.

[8]姜礼平,姚毅,邹明.威胁联网下低突防航路规划研究[J].海军工程大学学报,2008,20(4):51-54.

[9]张淘沙,鲁艺,吕跃.威胁联网下的飞行器航迹规划研究[J].电光与控制,2014,21(9):29-33.

[10]任佳,高晓光,郑景嵩.复杂环境下的无人机任务决策模型[J].系统工程与电子技术,2010,32(1):100-103.

[11]任佳,杜文才,白勇.基于贝叶斯网络自适应推理的无人机任务决策[J].系统工程理论与实践,2013,33(10):2575-2582.

[12]BARUA S,GAO X D,PASMAN H,et al.Bayesian network based dynamic operational risk assessment[J].Journal of Loss Prevention in the Process Industries, 2016,41:399- 410.

[13]SONG Y B,VAN DER SCHAAR M.Dynamic network formation with incomplete information[J].Economic Theory,2015,59:301-331.

[14]KUMAR S,TRILATHI B K.Modelling of threat evaluation for dynamic targets using Bayesian network approach[J].Procedia Technology,2016,24:1268-1275.

[15]史建国,高晓光.动态贝叶斯网络及其在自主智能作战中的应用[M].北京:兵器工业出版社,2008.