压缩感知联合多属性关联的数据恢复算法

,,

(海南大学 信息科学技术学院,海口 570228)

0 概述

在无线传感器网络(Wireless Sensor Network,WSN)中,参数信号大都具有非稳定性、不确定性以及大时滞等特性,导致传统的修复方法如多项式递推法、差分法、卡尔曼滤波法以及最小二乘法在数据恢复效果上并不理想。目前,压缩感知理论[1]已经逐渐被人们使用在信号恢复重建工作上,压缩感知理论是一种别于传统信号压缩理论的一种新理论,它利用信号的稀疏特性,通过非线性重建的算法来重建信号,并且它能使压缩过程与采样过程同时进行,而在压缩比较大时也能够获得较为理想的恢复效果。

信号如何进行稀疏表示,测量矩阵如何构造以及重构算法如何设计是压缩感知理论的3个核心内容。信号具有可压缩性能是压缩感知理论中的必须要求,而信号的稀疏表示则是该要求的具体体现。想要获得较好的可压缩性,需要依赖稀疏字典的设计,而为了得到与原始信号相匹配的优化字典,需用应用一定的学习算法来弥补先验知识的不足。压缩采样后获取的信息量受到测量矩阵构造的影响,测量矩阵的有限等距特性[2](Restricted Isometry Property,RIP)是测量矩阵构造的必要条件,在此条件的基础上专家学者提出了更广泛的构造原则,在不同的编码方式与构造方式的情况下,都能够几乎精确地重构原始信号,并且重构的信号具有唯一性。

原始信号经过压缩采样,依旧能够保留其重构所必要的信息,但光凭这些信息是远远不够的。信号重构问题一直以来就是个NP难的问题,为了让信号重建成为可能,利用了在重构过程中,信号的稀疏性以及信号具有有限个的非零系数这2个特性。随着压缩感知理论的推广普及以及深入研究,目前出现了各种优化的重构算法,主要为凸优化算法和贪婪算法等,凸优化算法包括基追踪算法(Basis Pursuit,BP)[3]、梯度投影算法[4]、内点迭代法[5]等,该类算法在重构精度上较有优势但其运算时间过长。较为常见的贪婪算法有正交匹配追踪(Orthogonal Matching Pursuit,OMP)[6]、分段正交匹配追踪(Stagewise Orthogonal Matching Pursuit,StOMP)[7]、正则化正交匹配追踪 (Regularized Orthogonal Matching Pursuit,ROMP)[8]、压缩采样匹配追 (CompressiveSampling Matching Pursuit,CoSaMP)[9]、子空间追踪(Subspace Pursuit,SP)[10]和稀疏度自适应匹配追踪 (Sparsity Adaptive Matching Pursuit,SAMP)[11]等,该类算法在运算速度上有较好的优势,但其运算的精度有限。由于信号重构是用于无线传感器网络这种实际应用中,数据需要具有实时性,因此数据的恢复重构在运算速度方面较为重要,而如何在确保运算速度的情况下提升数据恢复的精度是本文研究的主要内容。

在上述贪婪算法中,除了SAMP算法以外,其余算法需要预先假设信号是稀疏的并规定稀疏度。然而,在实际的信号恢复重构问题中,稀疏度往往很难获得。因此,本文提出一种改进SAMP算法,并借助多属性间存在的相关性来协助数据恢复。

1 压缩感知理论及其重构算法

1.1 压缩感知理论

(1)

其中,θ被称作投影系数向量,θ=ΨTX。如果θ的l0范数远远小于N,即非零项有限且很少,那么可以称信号向量X在矩阵Ψθ上是稀疏的,即信号向量X是可压缩的,信号向量X的稀疏度用K=‖θ‖l0来表示,其中‖·‖l0表示向量的l0范数。

在信号稀疏表示后,需要确定随机测量矩阵ΦM×N,该随机测量矩阵需要拥有RIP特性,并且跟信号的稀疏基不相关。确定随机测量矩阵之后,便可对信号X进行压缩采样,其压缩采样过程表示为:

Y=ΦM×NX=ΦM×NΨθ

(2)

其中,M为随机测量个数,向量Y为测量信号向量。随机测量个数M远远小于N,即信号的随机测量过程实则是对信号的压缩过程。信号进行随机测量后,把得到的结果用l0范数优化,重新把原始信号向量X进行重构:

min‖θ‖l0s.t.Y=ΦM×NΨθ

(3)

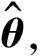
然而根据统计理论和组合优化理论得知,组合优化是一个NP问题,当N很大时,数值上无法有效实现,且抗噪声能力很差,因此,由一些研究者证明l0约束优化问题可以转为数值上容易处理l1约束的凸优化问题:

min‖θ‖l1s.t.Y=ΦM×NΨθ

(4)

其中,‖·‖l1表示向量的l1范数。基于l1范数凸优化算法的系数重构模型一般采用:

min‖X‖l1s.t. ‖Y-ΦM×NX‖l2≤σ

(5)

其中,σ为残差,‖·‖l2表示向量的l2范数。即对式(5)进行多次重复迭代,设定一个合理的残差上限,当迭代后的残差小于等于残差上限时,用最小二乘法便可求出x的广义解。

1.2 SAMP算法

鉴于大部分算法都需要已知信号的稀疏度,而实际问题中稀疏度往往是未知的,SAMP算法便可很好地解决这种问题。该算法在稀疏度无法确定时,设定初始步长与初始稀疏度,在每次迭代后可以得出一个残差值,把得出的残差值进行对比,从而更新步长以及稀疏度,如此反复得出稀疏的一个最优估计,实现信号的压缩重构。但是该算法仍然有一定的缺陷,如果设定稀疏度的初始值相对于实际值过于偏小,便会导致迭代次数增多,即会影响到运算时间,在实际应用中会有比较大的影响。如果设定步长的初始值相对于实际值过于偏大,那么会导致可能无法获得真实稀疏度的值,使结果存在一定的误差,从而降低了重构精度。因此,需要一种改进的算法来解决上述的问题。

2 基于压缩感知和多属性协助的改进算法

2.1 改进的SAMP算法

为了解决SAMP算法带来的缺陷,将原稀疏信号向量X进行分块得到多个子信号,把分出的子信号逐一重构再合并得出整体的重构信号。由于原始稀疏信号向量X稀疏度越低在运用同样重构算法的前提下重构精度越高[12]。如式(6)所示,利用信号整体是稀疏的,因此,局部也是稀疏的特性,将信号向量X分为多个相同长度的子信号,每一个子信号作为一个统一体来进行运算。

(6)

由文献[13]中的理论得,当观测矩阵ΦM×N满足RIP性质时,可得如下公式:

(7)

其中,F0表示迭代的索引集合的初始值。利用命题成立则其逆否命题也成立的性质,可得:

(8)

因此,在K0初始化后如果满足式(8),则K0=K0+s,其中,s为步长,更新F0。重复式(8)直至条件不成立为止。将此算法命名为分段稀疏度自适应匹配追踪(Stagewise Sparsity Adaptive Matching Pursuit,SSAMP)算法。

2.2 多参数协助的改进算法

无线传感器网络获得的参数属性一般均为某一系统中的属性,而系统中的属性间往往存在一定的联系,比如在自然环境下,室内与室外的温度与湿度间就具有一定的线性关系[14]。然而这些关系较为复杂,在绝多数情况是无法用一个简单的函数式子去把它们表示出来。因此,本文使用联合稀疏分解的方法把多种参数的信号融合并提出共同分量和特征分量2个部分的方法来表现无线传感器网络中不同属性间的相关性。若共同分量比之总体所占比例越高,则这些属性间的相关性也就越高。

通过研究信号群中信号内部和信号之间的相关性以及借助分布式信源编码的思想,文献[15]针对不同领域与用途提出了3种联合稀疏模型(Joint Sparsity Model,JSM),其中,JSM-1模型十分适合应用于无线传感器网络。

假设在无线传感器网络中多种不同的传感器组成一个传感器群,每个传感器群由一个传感器节点来接收数据并发送到汇聚节点。则在这个过程中令传感器节点一共有P个以及N个传感器组成的传感器群,即N个参数属性。由于在监测周期内有Q个时间隙,每个时间隙内为数据采集后各个节点采集到的信号向量的长度L,因此可以把采集到的数据用Q×P的矩阵的形式表示:

(9)

矩阵A的每一列矩阵Xi,i=1,2,…,P表示在该时间隙内,一个传感器节点得到的信号向量,矩阵A的每一行矩阵Xj,j=1,2,…,Q表示在同一采样时刻,所有传感器节点得到的采样信息。

在汇聚节点进行稀疏变换可得:

Xi=Ψθ,i=1,2,…,P

(10)

则正交基矩阵Ψ为Xi,i=1,2,…,P的稀疏基。反变换后,写成矩阵的形式得:

(11)

其中,矩阵B为稀疏变换后系数稀疏构成的矩阵,矩阵θi,i=1,2,…,P表示矩阵B的第i列,矩阵θj,j=1,2,…,Q表示矩阵B的第j行。

利用JSM-1模型进行联合稀疏表示,则矩阵θi可以写成另一种形式:

θi=Δc+Δi,i=1,2,…,P

(12)

为了使联合稀疏表示后稀疏度达到最小值,因此问题转化为求下式l0范数的最小化:

min(‖Δc‖l0+‖Δ1‖l0+…+‖ΔP‖l0)

(13)

设矩阵Δc(n),n=1,2,…,Q为共同分量的第n个元素,因此,如若求解稀疏度最小时对应的共同分量,只需令矩阵Δc(n)等于矩阵B的第n行的P个元素中出现频数最大的元素。

联合稀疏后的信号群矩阵变成如下形式:

(14)

将式(14)向量化,按列堆栈成一个Q(P+1)×1的列向量得:

(15)

设‖Δc‖l0=Kc,‖Δi‖l0=Ki,i=1,2,…,P,由共同分量和特征分量的稀疏度,由式(3)可以确定矩阵Δc,Δ1,…,ΔP所需的观测值个数Mc,M1,…,MP,其对应的随机测量矩阵为Φc,Φ1,…,ΦP,则测量值向量可以表示为:

Yc=ΦcΔc

Y1=Φ1Δ1

⋮

YP=ΦPΔP

(16)

(17)

将以上的算法命名为多属性压缩感知(Multipara-meter Compressed Sensing,MCS)算法。

3 算法的实现步骤

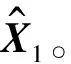
输入

1)观测矩阵Φ

2)传感矩阵Z=ΦΨ

3)观测向量X

4)初始步长s

输出

矩阵分块算法[9]如下:

For id_x=1:ceil(a/size);

For id_y=1:ceil(b/size);

XX= X((id_x-1)·size+1:id_x·size,(id_y-1)·

size+1:id_y·size);

X1=ww·sparse(XX)·wwT;x1=full(X1);

y=ΦX1;

For i=1:size;

信号重构步骤如下:

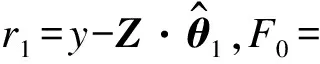
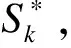
4)令Ck=Ft-1∪Sk,Zt={Zj}(for allj∈Ck);

5)求向量X=Ztθt的最小二乘解:

8)如果残差rtnew=0,那么停止迭代第3)步～第8)步进入第9)步;

(1)如果‖rtnew‖2≥‖rt-1‖2,更新步长I=I+s,返回第3)步继续迭代;

(2)如果前面2个条件都不满足,那么Ft=F,rt=rtnew,t=t+1,如果t≤P停止迭代进入第9)步,否则返回第3)步继续迭代;

矩阵分块算法如下:

X2(:,i)=x;

End

X3((id_x-1)·size+1:id_x·size,(id_y-1)·

size+1:idid_y·size)=wwT·sparse(X2)·ww

End

End

在上述的步骤中,a是x的行数,b是x的列数,size是分块的大小,Ø是空集符号,∪是并集运算符号,〈·,·〉是2个向量求内积,abs[·]是求模值,即绝对值,rt表示迭代残差,t表示迭代的次数,Ft表示t次迭代的列序号集合(元素个数为I,I等于整数倍步长s),Zj表示矩阵Z的第j列,Zt={Zj}(for allj∈Ck)表示通过列序号集合Ck选出的矩阵Z的列集合(设矩阵的列数为It),θt为It×1的列向量。

4 实验仿真

实验1SSAMP算法的信号重构效果

本文实验采用信号长度L=256的稀疏信号,观测矩阵是压缩维度为128的高斯随机矩阵,非零系数的大小服从高斯分布。图1是通过SSAMP算法重构的信号与原始信号对比图,其恢复残差ans=1.285e-14,运行时间为0.070 570 s。由于信号为随机生成,每次结果均不相同,但经过多次实验,其恢复残差均满足ans≤3e-14。

图1 SSAMP算法重构信号效果

实验2MCS- SSAMP算法的信号重构效果

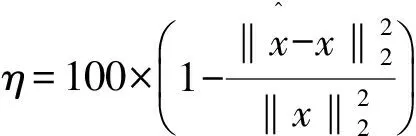
首先实验观测稀疏度k对重构精度的影响,规定对每一个观测值重复测验m=128次,得出稀疏度10≤k≤70时各个不同算法对于重构精度的影响,如图2所示。实验证明,随着稀疏度k的降低,各个算法的重构精度会不断提高,而MCS-SSAMP算法提高的速度明显快于其他算法,并且当稀疏度在k=52时,该算法就已经可以达到重构成功的水平,而其他算法达到重构成功水平所需要的稀疏度区间均小于MCS-SSAMP算法。

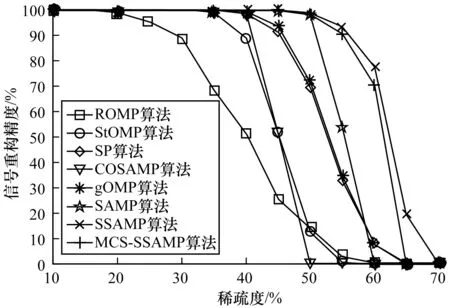
图2 稀疏度与信号重构精度的关系

其次实验观测测量数m对重构精度的影响,令稀疏度k=20,得出测量数50≤m≤100时,各个不同算法对于重构精度的影响,如图3所示。实验证明,随着测量数m的增加,各个算法的重构精度会不断提高,而MCS-SSAMP算法提高的速度明显快于其他算法,并且当测量数m=68时,该算法就已经可以达到重构成功的水平,而其他算法达到重构成功水平所需要的测量数区间均小于MCS-SSAMP算法。

图3 测量数与信号重构精度的关系

5 结束语

本文研究水产养殖中数据的恢复问题,提出一种数据恢复算法。采用原始稀疏信号分块重构,使用最佳的汇聚节点确定出共同分量,并进行联合编码,降低每轮迭代当中要处理的信号稀疏度,从而用更少的测量值实现信号群的精确重构。改进的算法在运算时间上,由于对信号的初始稀疏度做了初始估计,因此可以有效避免稀疏度的初始值相对于实际值过于偏小时,导致迭代次数增多的问题。实验结果表明,该算法降低了运算的时间,使运算更加高效,测定精度更高。今后将着重于研究用何种算法选取效率比较高的次属性,以进行协助数据恢复的工作。

[1] DONOHO D L.Compressed sensing[J].IEEE Transactions on Information Theory,2006,52(4):1289-1306.

[3] CHEN S S,DONOHO D L,SAUNDERS M A.Atomic decomposition by basis pursuit[J].SIAM Review,2006,43(1):129-159.

[4] APPLEBAUM L,HOWARD S D,SEARLE S,et al.Chirp sensing codes:deterministic compressed sensing measure-ments for fast recovery[J].Applied & Computational Harmonic Analysis,2009,26(2):283-290.

[5] ROMBERG J.Compressive sensing by random convolution[J].SIAM Journal on Imaging Sciences,2009,2(4):1098-1128.

[6] TROPP J A,GILBERT A C.Signal recovery from random measurements via orthogonal matching pursuit[J].IEEE Transactions on Information Theory,2007,53(12):4655-4666.

[7] DONOHO D L,TSAIG Y,DRORI I,et al.Sparse solution of underdetermined systems of linear equations by stagewise orthogonal matching pursuit[J].IEEE Transactions on Information Theory,2012,58(2):1094-1121.

[8] NEEDELL D,VERSHYNIN R.Signal recovery from incomplete and inaccurate measurements via ROMP[J].IEEE Journal of Selected Topics in Signal Processing,2010,4(2):310-316.

[9] NEEDELL D,TROPP J A.CoSaMP:iterative signal recovery from incomplete and inaccurate samples[J].Applied & Computational Harmonic Analysis,2008,26(3):301-321.

[10] DAI W,MILENKOVIC O.Subspacepursuit for compressive sensing signal reconstruction[J].IEEE Transactions on Information Theory,2009,55(5):2230-2249.

[11] DO T T,LU G,NGUYEN N,et al.Sparsity adaptive matching pursuit algorithm for practical compressed sensing[C]//Proceedings of Asilomar Conference on Signals,Systems,and Computers.Washington D.C.,USA:IEEE Press,2008:581-587.

[12] 闫 鹏,张志贤,王阿川.基于压缩感知SAMP算法的改进[J].森林工程,2014,30(3):80-83.

[13] 杨 成,冯 巍,冯 辉,等.一种压缩采样中的稀疏度自适应子空间追踪算法[J].电子学报,2010,38(8):1914-1917.

[14] LAWRENCE M G.The relationship between relative humidity and the dewpoint temperature in moist air:a simple conversion and applications[J].Bulletin of the American Meteorological Society,2010,86(2):225-233.

[15] BARON D,DUARTE M F,WAKIN M B,et al.Distributed compressive sensing[C]//Proceedings of International Conference on Acoustics,Speech and Signal Processing.Washington D.C.,USA:IEEE Press,2009:2886-2889.