电容抽头在高频电路中的应用与等效计算
2018-04-19吴元亮
吴元亮,徐 勇,闵 锐
(陆军工程大学通信工程学院,南京 210007)
1 部分接入的工程背景与教学意义
滤波器和阻抗匹配是高频电路设计的两类重要电路。信号在传输过程受到噪声和干扰,滤波器从众多无用信号和噪声、非线性失真等干扰中选出有用信号,同时抑制和滤除无用信号和噪声干扰。阻抗匹配则实现从信号源到负载的最大可能功率转移,尤其是在高灵敏度接收机的前端[1]。这两类电路通常由电感和电容组成,往往以部分接入方式应用在天线、调制器、高放、混频器等电路的输出端。部分接入一是减小源和负载对LC谐振回路的影响,提高高频电路选频能力、解决谐振频率漂移和不稳定问题,二是实现阻抗匹配,方便信号传送到下一级。
2 源和负载对LC谐振回路的实际影响

图1 源和负载对LC谐振回路的影响
直接插入信源、负载时,谐振频率f0、有载品质因数QL计算为:
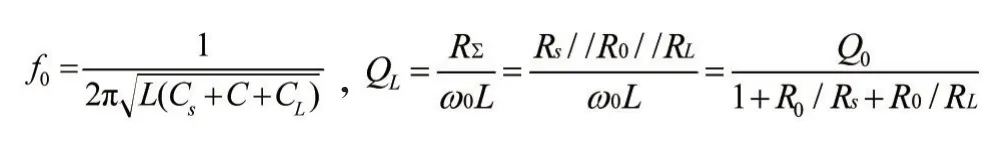
f0的计算式表明源电容CS和负载电容CL将导致f0减小,若维持f0不变,需要减小电感L,这必然降低QL,进而降低回路的选频能力。QL的计算式表明源内阻Rs和负载电阻RL的引入将减小LC回路总电阻RΣ和有载品质因数QL,增大带宽B,这使得LC回路很难适用于小阻值源和负载时。部分接入是有效解决这个问题的方法之一。
3 部分接入的阻抗变换与准确计算
部分接入主要有图2所示3种方式:变压器、电感抽头和电容抽头。对于每一种形式,折算均可使用公式,公式可推广应用于,n为接入系数,互感,电感抽头,电容抽头。部分接入将大大提高电路的品质因数,是一种行之有效的改进方式。

图2 常用的3种部分接入方式
但是高频电路教学对于折算公式的准确运用鲜有提及。图3为一道带有负载电容的电容抽头接入电路[2],学生在计算上存在一定争议。

图3 电容抽头接入电路
学生采取两种计算思路。思路一:负载电阻RL与负载电容CL标为负载阻抗ZL;思路二:负载电容CL与回路电容CL直接合并。计算的结果如表1所示。
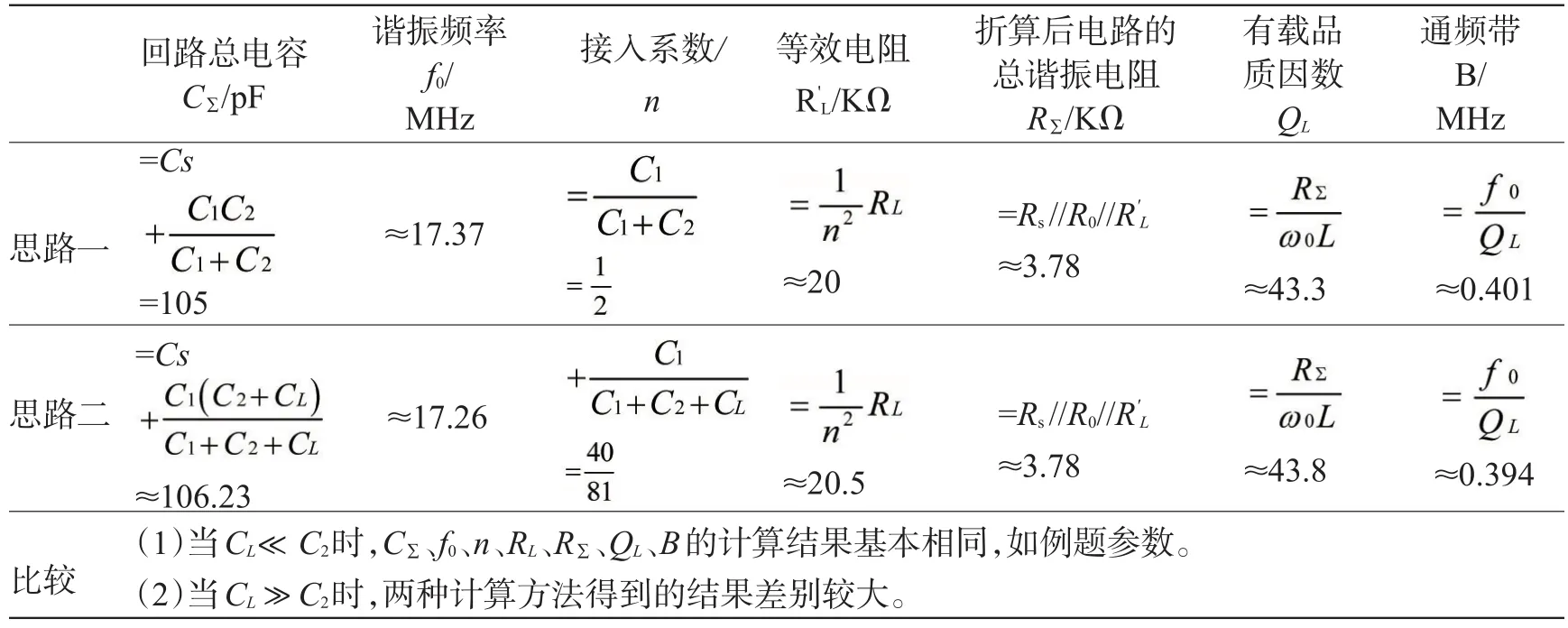
表1 两种计算思路的结果比较
处理负载电容,计算思路一依据电路基本理论,思路二则是高频电路等效计算的常用方法。针对例题,表1中两种计算结果相近,但是有差别,而且差别随着负载电容CL的增大而增大,当CL的值接近甚至大于抽头电容C2时,差别很大。
通过图4所示电容抽头接入方式的阻抗等效过程解释和解决计算争议问题。

图4 电容抽头接入方式的阻抗等效计算
根据电路串并联转换的阻抗变换原则,有如下计算。
ZL、C2并联向串联转换
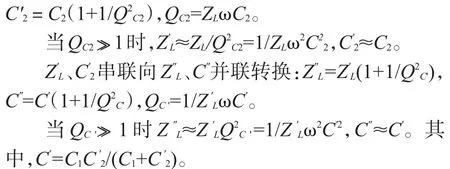
负载电容CL越大,负载阻抗ZL越小,QC2越小;抽头电容C2越小,QC2越小。QC'情况与QC2相似。而QC2、QC'越小,根据等效计算公式计算的结果就越不准确。因而,为等效计算准确性高,抽头电容应该比负载电容取值大一些,表1结果也表明了这一结论。
4 电容抽头部分接入Multisim电路仿真
图5为纯电阻负载时,LC谐振回路直接接入与部分接入的电路性能对比。仿真结果表明:部分接入方式能够有效提高电路的品质因数,选频曲线更陡峭,带宽变窄[3-4]。
图6为负载有电容时,不同负载电容值对电路性能指标的影响。仿真结果表明:抽头电容为20 pF,负载电容为1 pF时,电路谐振频率、品质因数等各项指标受负载电容的影响很小,谐振频率与LC谐振回路空载时谐振频率相近,品质因数与纯电阻负载越相近;负载电容越大,各项指标受负载电容的影响越明显。从而证明利用高频电路中的折算公式计算谐振频率、谐振电阻、品质因数、带宽等指标时必须充分考虑负载电容与抽头电容在取值方面的关系,以免计算结果误差较大。

图5 直接接入与部分接入的性能对比
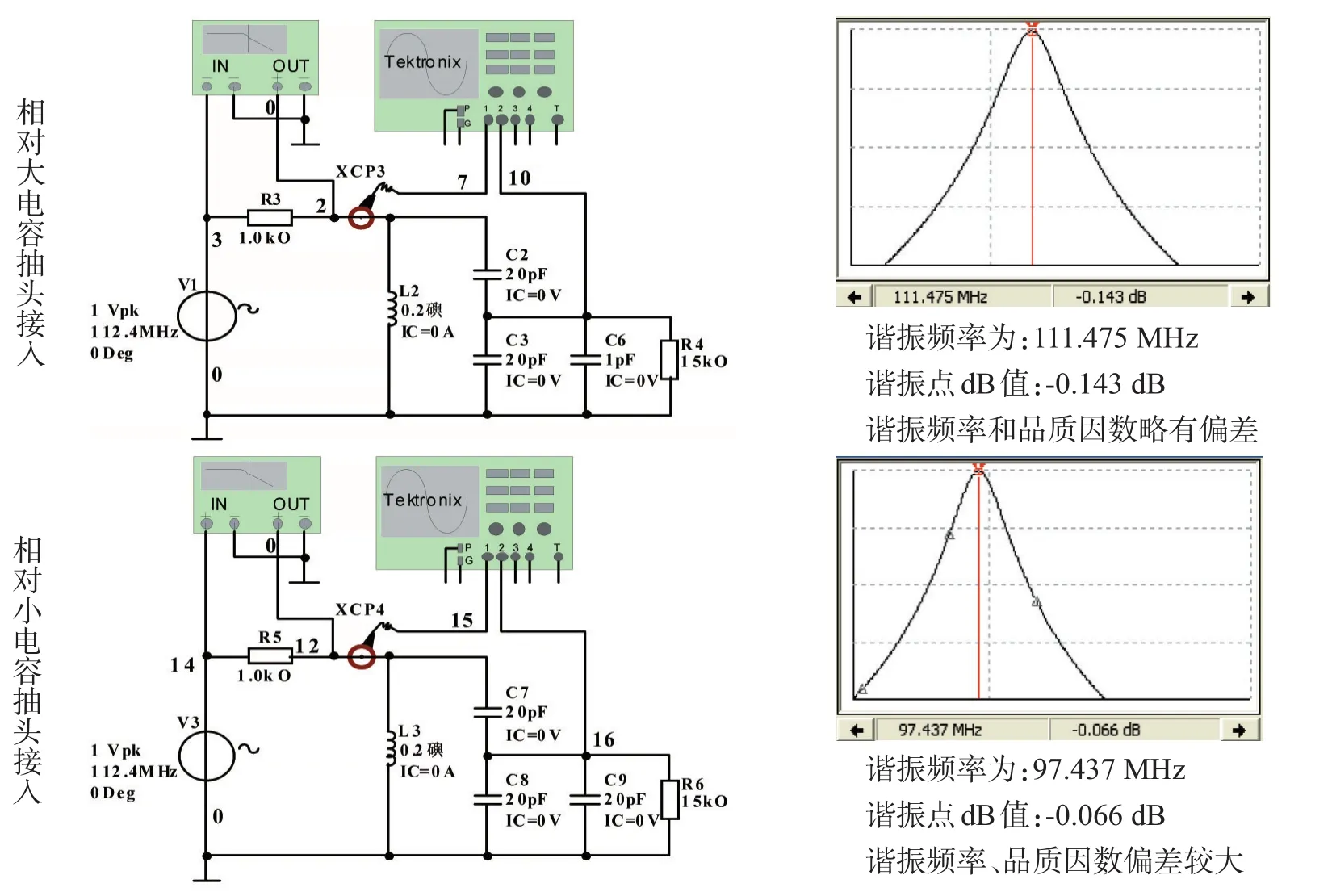
图6 抽头电容一定时不同负载电容对性能指标的影响
5 结语
高频电路中应用LC回路时往往采取部分接入方式,以降低源与负载阻抗的影响。针对电容抽头接入的等效计算问题,讨论根据电路理论和部分接入常用等效公式计算的差别,并分析差别产生的原因,最后利用电路仿真软件验证了理论分析的准确性。
参考文献:
[1]CHRISTOPHER B,JOHN B,CHERYL A.射频电路设计[M].北京:电子工业出版社,2015.
[2]徐勇,吴元亮,徐光辉,等.通信电子线路[M].北京:电子工业出版社,2017.
[3] 陶玉贵.Multisim仿真在高频电子技术教学中的应用[J].西昌学院学报(自然科学版),2015,29(3):150-152.
[4] 吴学军.基于EDA仿真技术的《模拟电子技术基础》课程教学[J].西昌学院学报(自然科学版),2015,29(1):157-160.
