无缝二维基准转换模型研究
2018-04-19罗琳,文展,罗枫
罗 琳,文 展,罗 枫
(1.四川工商学院,成都 611745;2.四川路桥,四川 广安 610041;3.中铁二院工程集团,成都 610031)
在使用GPS、在空间大地测量和工程应用中经常涉及到不同坐标系坐标成果之间的转换。但是工程测量中,目前仍为2+1维,因而平面二维坐标转换是经常需要用到的。
1 最小二乘法
通常二维基准转换模型在求解坐标转换参数时,往往只考虑了公共点在一套坐标中的误差,而忽略了其在另一套坐标系中的坐标误差,得到线性基准转换模型之后,实际情况下,观测误差服从正态分布,采用最小二乘方法,求解出转换参数的最优估值。近年来,有许多学者在传统基准转换的基础上研究了同时考虑公共点在两套坐标系中的坐标误差的基准变换模型,并研究了整体最小二乘解法[1,4,7,8]。
本文分析了基于整体最小二乘原理的转换模型[1]。模拟实际情况下,公共点只知道其在一套坐标系中的权阵,假定在一套坐标系中公共点的权阵不为单位阵而在另一套坐标系中的权阵假定为单位阵,再基于整体最小二乘原理进行坐标转换。同时,根据李博峰提出的无缝三维基准转换模型[2]的数和旋转参数,为第i点的二维坐标,下标Ⅰ和Ⅱ表示两套坐标系。上式也可以改写为:
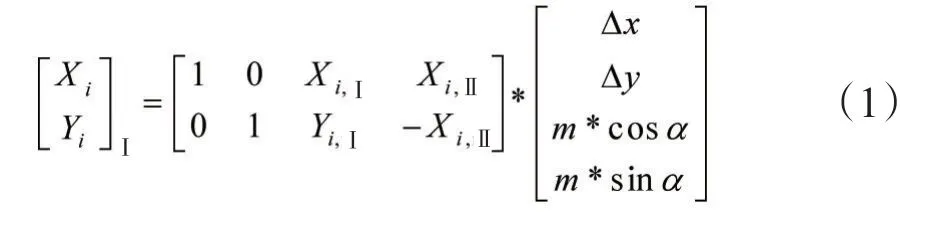
由于两套坐标都是测量平差到的,它们不可避免地受到观测误差的影响,因而对两套坐标引入误差向量:

联合各公共点求解转换参数,则有:

求解转换参数的本质是拟合求解出两套坐标系公共点之间的确定性函数关系,其最终目的是计算出非公共点的第Ⅱ套坐标,假设转换时有m个非公共点,则它们的第二套坐标可以表示为:


假设相同坐标系的坐标误差相关而不同,坐标系的坐标误差独立,在坐标误差服从零均值正态分布的条件下,上式各项误差的随机模型表示为:

其中,vec(·)为矩阵向量化子。
2 拟合推估法
拟合推估模型[4]的标准形式为:

式(9)中,y是n×1维观测向量,ey是观测向量对应的误差向量;β是k×1阶的参数向量,C是列满秩设计矩阵,y0表示n0×1未知随机信号向量,ey0是它的误差向量,C0是设计矩阵。值得注意的是,通常我们要求n>k,但并不需要n0>k。上述的模型包含“平差”和“预报”两个过程,平差指用观测向量y来估计参数β;而预报则是根据信号y0和β参数的函数关系以及其与观测向量y的随机关系来对y0作出合理的推估。

基于最小二乘原理:

3 基准转换模型的联合求解
二维基准转换联合模型是一种非线性模型,本文在高斯-牛顿法的基础上将其转化为线性模型[5],然后采用拟合推估法求解。
3.1 基于高斯-牛顿法的线性模型
采用高斯-牛顿法将非线性模型转换为线性模型,然后迭代求解。假设第j次迭代后的估值表示为ξ(j),那么参数ξ就可以表示为:

其中δξ(j)为第j+1次迭代的参数的修正数,将式(13)带入坐标转换模型可得:

方程(15)中如果只对δξ进行迭代,则会造成因省略二次项EA,δξ以上的小项造成的迭代发散或收敛错误,所以应该同时对EA,δξ一起迭代。设EA的第j次迭代值为EA(j)。
将参数求解的矩阵方程式转换为拟合推估的标准形式为:
其中,I2n和I2m分别代表2n维和2m维的单位阵指的是kronecker积算子,上述的推导利用了矩阵积向量转换关系式∶


ξ(j)是方程线性化后ξ第j次的迭代值由协方差传播定律导出方程的随机模型为:

由公式(16)、(17)和(18)可以推导出:

由于上式中前两个公式用于参数估计,后两个公式用于计算非公共点的第Ⅱ套坐标,并且因为“预报”和“估计”是相对独立的过程,因此在实际计算中只需按照前两公式迭代计算转换参数的最优值,迭代终止后,按(17)、(18)计算最终的坐标推估值。
3.2 系数误差协方差阵的计算
上述模型的求解需要已知系数阵误差的协方差阵QAA和QBA,即:

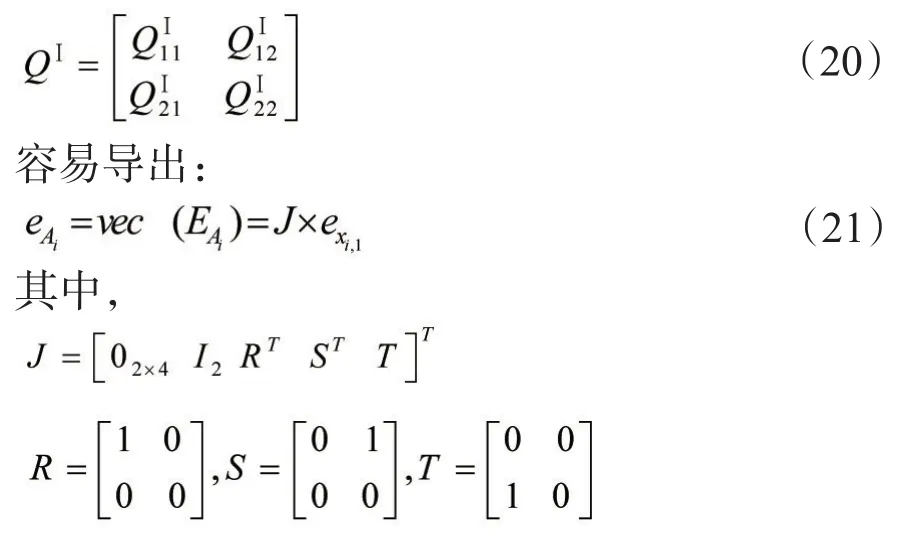
根据误差传播定律得:

4 传统基准转换模型
传统基准转换模型只考虑了公共点的第二套坐标误差且忽略了非公共点坐标误差,其标准形式为:

5 基于整体最小二乘原理的坐标转换模型
鲁铁定在其博士学位论文[6]中详细推导了基于整体最小二乘原理的坐标转换方法带权整体最小二乘即考虑公共点的两套坐标权阵基于的条件进行参数的求解,其中v1和v2分别表示公共点在两套坐标系中的坐标误差。不带权整体最小二乘即不考虑公共点的任何一套坐标系权阵进行在的条件下迭代求解转换参数。笔者认为,在实际工程应用的转换参数求解中,至少观测值对应的权阵是可以得到的,所以在参数求解时应该考虑其权阵,而不是忽略公共点在任何一套坐标系中的权阵而采用不带权整体最小二乘。当认为公共点在第Ⅱ套坐标系中的权阵即观测值的权阵不为单位阵,公共点第Ⅰ套坐标系中的权阵假定为单位阵时,参数求解基于的条件。参数的求解方法为(略去公式推导过程):

其中

当认为公共点在第Ⅱ套坐标系中的权阵即观测值的权阵不为单位阵,并且公共点在第一套坐标系中的权阵也不为单位阵时,即可利用最小二乘配置的方法迭代求解转换参数,这也就是无缝二维基准转换中的迭代计算转换参数的过程,只不过省去了后面对非公共点构成的系数阵的改正。
6 算例与分析
算例说明:因工程实例中的数据,均有误差,无法准确验证模型精度,只能通过与已有软件转换成果对比验证模型是否正确,本文主要研究无缝二维转换模型的精度,故使用模拟数据,得到真值后,人为加上正态误差模拟工程实际情况,然后转换得到成果与真值对比,比较三种模型的精度。
6.1 模拟数据
本次模拟数据共用了8个坐标:p1、p2、p3、p4、p5、p6、p7、p8。其中p1、p2作为基本点,只用来计算公共点和转换点的平差值及其对应的协因数阵,p3、p4、p5作为公共点,p6、p7、p8作为转换点。
①首先人为定义坐标系A中p1~p8各个点的合理坐标,然后用转换参将其转换到B坐标系当中,得到p1~p8点的坐标真值。
②在坐标系A中,计算出p1~p2外的任意两点距离真值共27条(p1,p2两点的坐标在计算中一直使用真值,因此其距离不参与平差),分别计算p1和p2到其余点的坐标方位角共12个,由此共得到39个观测值。
③给距离真值加上均值为0,中误差为σ1的随机数,给方位角真值加上均值为0,中误差为ε1的随机数。因而观测值的协因数阵为:

④根据参数平差计算过程计算p3~p8的坐标平差值,根据误差传播定律计算其对应的协因数阵QXX。
⑤同理,在B坐标系中,计算p1~p5各个点的距离真值共9条,分别计算p1,p2到其它3个点的方位角共6个,得到15个观测值。给距离真值加上均值为0,中误差为σ2的随机数,给方位角真值加上均值为0,中误差为ε2的随机数。因而观测值的协因数阵为:

⑥根据参数平差计算过程计算B坐标系中公共点p3~p5的坐标平差值,根据误差传播定律计算其对应的协因数阵QLL。
6.2 计算与分析
方案一:基于高斯-牛顿法的基准转换联合模型,迭代计算,对应图1~3。
方案二:基于整体最小二乘原理的坐标转换,迭代计算,对应图4~6。
将上述过程产生的公共点与非公共点坐标平差值以及它们所对应的协因数阵带入数平差计算,求出转换点在第Ⅱ套坐标系中的坐标之后与其真值求坐标的均方根σ。

将500次数据模拟结果绘制成函数图像,将无缝二维基准坐标转换与传统坐标转换,基于整体最小二乘原理的坐标转换与传统坐标转换精度结果绘制在一起,比较其转换精度。
图1~3显示:无缝二维基准转换模型相比传统坐标转换方式,能够得到更好的坐标转换精度,在合理的定权的时,无缝二维基准转换可以通过迭代求解进而极大地提高求解的转换参数精度,并对非公共点坐标构成的系数阵进行修正,获得满意的转换结果。图4~6表明:基于整体最小二乘的坐标转换虽然较传统的坐标转换方式有一些改进,但其效果并不明显。出现这种情况的原因是第Ⅰ套坐标系中的坐标权阵是单位阵,这是根据经验定权或没有明确得知第Ⅰ套坐标系中各个坐标的精度水平而假定各个坐标精度水平一致得出的结论。因此,在转换参数求解时得到转换点所在坐标系内坐标的协方差阵的准确值对于转换参数的准确求解是十分重要的,这也是在无缝二维基准坐标转换时得到满意成果的前提。当对第Ⅰ套坐标系内定权不合理时,利用无缝二维基准转换求解参数的精度水平将受到很大的影响。

图1 无缝二维基准坐标转换与传统坐标转换的精度比较σ1=0.1 cm,ε1=0.1″.σ2=0.3 cm,ε1=0.2″

图2 无缝二维基准坐标转换与传统坐标转换的精度比较σ1=0.5 cm,ε1=0.5″.σ2=1 cm,ε1=0.8″

图3 无缝二维基准坐标转换与传统坐标转换的精度比较σ1=1 cm,ε1=2″,σ2=2 cm,ε1=2″

图4 无缝二维基准坐标转换与传统坐标转换的精度比较σ1=0.1 cm,ε1=0.1″.σ2=0.3 cm,ε1=0.2″
7 结论
为在工程应用中得到更高精度的坐标转换成果,本文在无缝三维基准转换模型的基础上研究了无缝二维基准转换模型,通过数据模拟计算,检验了其和传统坐标转换模型以及与基于整体最小二乘原理的坐标转换模型的精度差异。得出如下结论:
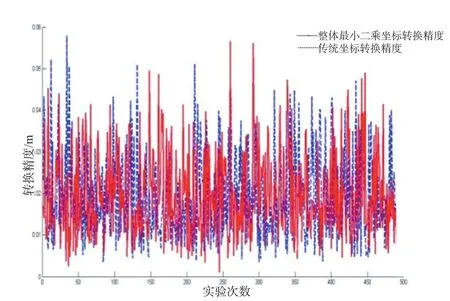
图5 无缝二维基准坐标转换与传统坐标转换的精度比较σ1=0.5 cm,ε1=0.5″.σ2=1 cm,ε1=0.8″

图6 无缝二维基准坐标转换与传统坐标转换的精度比较σ1=1 cm,ε1=2″.σ2=2 cm,ε1=2″
(1)为了顾及公共点在两套坐标系内的误差以及非公共点的坐标误差,本文基于无缝二维基准转换模型,将转换参数的求解与非公共点的转换联合处理,理论上是严密的二维坐标转换模型。
(2)与传统的二维坐标转换模型以及整体最小二乘基准转换模型的结果进行比较,实验表明无缝二维基准转换模型能取得更高的精度。
参考文献:
[1]简浩.顾及起算数据误差的整体最小二乘法及软件研制[D].成都:西南交通大学,2013.
[2] 李博峰,沈云中,李微晓.无缝三维基准转换模型[J].中国科学:地球科学,2012(7):1047-1054.
[3] 王文利,程传录,陈俊英.常用坐标转换模型及其实用性研究[J].测绘地理信息,2010,35(5):37-39.
[4] 李博峰.无缝仿射基准转换模型的方差分量估计[J].测绘学报,2016,45(1):30-35.
[5] 罗长林,张正禄,邓勇,等.基于改进的高斯-牛顿法的非线性三维直角坐标转换方法研究[J].大地测量与地球动力学,2007, 27(1):50-54.
[6]鲁铁定.总体最小二乘平差理论及其在测绘数据处理中的应用[D].武汉:武汉大学,2010.
[7] 王利朋,刘成龙,刘胜,等.坐标参数化的平面基准转换方法[J].武汉大学学报(信息科学版),2016,41(10):1409-1413.
[8] 林鹏,刘超,高井祥,等.附加约束的三维基准转换的高斯-赫尔默特模型[J].中国矿业大学学报,2017,46(5):1152-1158.
