面向海量数据的改进最近邻优先吸收聚类算法
2018-04-19,,
,,
(1.杭州电子科技大学 自动化学院,杭州 310018; 2.浙江省电子信息产品检验所,杭州 310007)
0 概述
聚类[1]是将对象集分成由类似对象组成的多个聚簇的过程,常用于统计分析方法,目前已经在图像识别、模式识别、数据挖掘等诸多方面大规模应用。
随着互联网的兴起和数据库技术的发展,数据集的规模不断扩大,传统的聚类方法因限于运行速度和准确率无法适用于大规模的数据集。以MapReduce[2-3]为代表的并行化编程框架的出现,为聚类算法应用于大规模数据集提供了一种新的途径。其中,文献[4]提出利用MapReduce对生物医学概念之间的关联进行提取的方法,文献[5]将MapReduce应用于数据分类方向,并对MapReduce进行稳定性测试。
目前已经有很多算法实现在MapReduce框架上,如使用范围最广的K-means算法[6-7],其中具有代表性的改进有基于MapReduce模型的单通和线性时间K-均值聚类算法[8]和基于海量数据分析的改进K-Medoids算法[9]。
MapReduce框架上较为常见的算法还有Canopy聚类算法,其中最具代表性的是文献[10]提出的改进Canopy高效算法。该文将改进的Canopy算法实现在Hadoop平台上,极大地节省了聚类运行的时间。
上述2种算法各有优劣:K-Means算法原理简单、便于操作,但类别数需要人为设置,而且初始聚类中心也很难选择,容易出现局部最优的情况;Canopy算法无需指定类别数,运行速度极快,适合处理大规模的数据集,但聚类效果一般,尤其是在不同类别的边界,极容易出现聚类重叠的现象。
文献[11]提出最近邻优先吸收(Nearest Neighbor Absorption First,NNAF)聚类算法,该算法适用于任意形状的聚类,可快速处理高维数据,但在数据密度和聚类间距离不均匀时聚类质量较差,文献[12]针对此问题提出基于数据分区的NNAF算法。本文在上述研究的基础上,基于MapReduce对NNAF算法进行改进。首先将其与Canopy算法结合,减少算法计算量,然后采用MapReduce编程框架对算法做并行化编程[13],使其能够支持海量数据处理。
1 最近邻优先吸收聚类算法
NNAF算法是一种最短距离聚类的算法,它是基于“同类相近”的思想提出的,其基本设计思路是:空间中的每一个点和与之距离最近的那个点,属于同一类的可能性是最大的。如果2个距离最近的点之间的距离小于d(距离阈值,由用户自己指定),那么就把它们分在同一类,当聚类里面包涵的元素个数大于q(数量阈值,由用户自己指定),则此数据集合就成为一个聚类。
NNAF算法的难点是2个阈值的选择。距离阈值过大会出现内圈稀疏、外圈密集的可能,不利于发挥出最好的聚类效果;距离阈值过小可能会使得聚类数量过多,起不到聚类应有的作用。而数量阈值的设定不合理,则会出现聚类过大或者过小的问题。
NNAF算法首先选择一个点,令其单独成为一类,将该点的所有最近邻点和以该点为最近邻点的点归入此类;然后以新加入的点为基准,将这些点的最近邻点和以这些点为中心的最近邻点的点归到这一类。不断重复上述步骤,直到点的数量满足设定的数量阈值。具体步骤如下:
1)设定距离阈值d和数量阈值q,输入数据集V。
2)调用SNN算法[14]计算出每一点的最近邻点。
3)随机选择数据集中的某一点,将其赋给新的点集P(P原为空集),并将该点从原数据集V中删除。
4)将该点的所有最近邻点和以该点为最近邻点的点都赋值给P,并将这些点从原数据集V中删除。
5)将新加入点的最近邻点和以这些点为最近邻点的点都赋值给P,并将这些点从原数据集V中删除。
6)当P中的个数满足数量阈值q时,结束对这个类的访问。
7)从V中选择一个点,重复步骤3)~步骤6)。
8)直到所有的点都被聚类,即V变成空集,结束所有操作,输出这些类。
2 最近邻优先吸收算法的改进
2.1 基于Canopy算法的改进
Canopy[15]算法是一种新的聚类方法,它可以通过使用一种简单的距离计算方法把整个数据集合分成几个相互重叠的子集,从而有效地减少数据的计算量。Canopy算法对处理海量数据有着极大帮助,其伪代码如下:
Begin
canopy=[]
load list
[m,n]=size(list)/*获取list中向量的数量*/
load T1,T2;T1>T2
for i=1:m;i++
A=randperm(list)/*随机从list中取一点A*/
delete A from list
for j=1:m-1;j++
d=pdist2(A,list(j))/*计算A与list中其他某一向量的距离*/
if d<=T1
put A into canopy
S(i)=canopy
end
if d<=T2/*判断距离是否小于T2*/
delete list(j) from list/*将其从list中删除*/
end
end
if list=[]
break
end
本文提出的改进NNAF算法,通过Canopy算法得到子集之后,对子集中相互重叠的部分采用最近邻优先聚类算法进行计算,从而达到减少计算量和提升准确率的目的。具体步骤如下:
1)将数据集向量化,并按照任意的固定规则排序,得到一个list,然后再选择2个距离阈值:T1和T2,其中T1>T2,T1和T2的值能够用交叉校验来确定。
2)从list中任取一点P,用低计算成本方法快速计算点P与list中所有向量之间的距离,如果点P与某个向量之间的距离在T1以内,则将点P和这个点加入到一个Canopy。
3)如果点P曾经与某个Canopy的距离在T2以内,则需要把点P从list中删除,此步认为点P已经确认基本属于该Canopy,因此,不可以再利用这个点去做其他Canopy的中心。
4)重复步骤2)和步骤3),直到list为空,结束。
5)采用SNN算法确定2个Canopy交叉部分的数据集V(如图1所示)中每一点的最近邻点,以及以数据集V中的点为最近邻点的点。
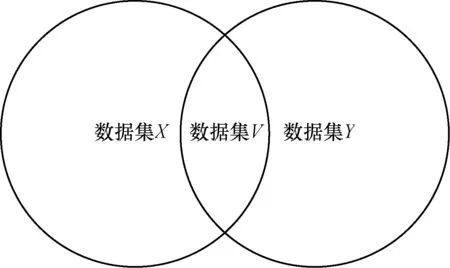
图1 聚簇交叉情况
6)随机从数据集V中取一个点,找到其最近邻点,依据这个最近邻点所属类别来判断该点的类别。如果最近邻点也没有确定类别,则开始寻找以此点为最近邻点的点,根据其所属类别来判断该点的类别。如果以此点为最近邻点的点不止一个,且分属不同的类,则依据它们到此点相对距离的远近来判断该点属于哪一类。如果还是无法判断,则换另外的一个点;如果数据集V中所有的点都无法判断,则将数据集V单独列为一类。
7)判断完毕之后,将该点从数据集V中删除,并归入到所属的数据集中。
8)从V中再随机找到一个点,重复上述步骤,直到V为空,停止。
9)对数据子集进行归并整理,得到的结果就是聚类结果。
在NNAF算法中,若起始点选取不当可能就会出现局部最优解的问题,而使用Canopy算法则可以避免这个问题。在采用Canopy算法得到粗聚类结果之后,可以直接对聚簇交叉的地方进行起始点选取,避免起始点选择不当的问题。
此外,NNAF算法的计算量较大,这主要是体现在计算每个点最近邻点的时候,这种计算方式在处理少量的数据时,并无任何不当之处,但是当数据规模增大之后,其计算难度就会激增,计算时间也会变得极长,这也是它无法直接应用在海量数据处理上的原因。而在采用Canopy算法进行改进之后,可以通过数据处理将数据集分成数据子集,并使用Canopy算法产生一定数量的Canopy中心,将各个数据子集的Canopy中心进行集合,然后再次利用Canopy算法处理这些中心点(此时使用的是新的T1、T2),得到的就是全局的Canopy中心集合,最后利用这些点对原始的数据集进行处理,生成多个相互之间有重叠的Canopy(聚簇),从而可以直接处理子集的重叠部分,减少计算量。
2.2 算法MapReduce化
MapReduce是Google提出的一种并行编程框架,它可以通过Map(映射)和Reduce(约减)2个过程来将具体的计算过程并行化,并分布在不同的机器上进行计算。
本文算法的MapReduce化主要应用于2个方面:1)对整体数据集的分割,在整体数据集过大的情况下,可以通过MapReduce对数据集进行分割,然后对分割后的数据集进行并行处理,进而达到处理海量数据的效果;2)对Canopy交叉集合的处理,通过对交叉集合的同步并行处理,减少运行时间,达到实时性的要求。
“肖玉那样一根筋的人,她说是不用我负责,要是犯了傻,完事再自杀呢?俺可担不起这个责任,想得开的小妞有的是。”
本文改进算法的具体结构框架如图2所示,该算法主要分为2个阶段:
阶段1采用Canopy算法得到相互之间有交叉的聚簇,此部分的MapReduce化主要体现在对数据集本身的处理上:首先对数据集向量化,进行分割并确定阈值;然后将分割后的数据集分布在不同的平台上,采用Canopy粗聚类得到所有聚簇的中心点;最后再将每个平台产生的聚簇中心点汇总,确定新的阈值,并利用新的阈值对中心点的集合进行聚类,将最终得到的聚类结果应用在总的数据集上。此时得到的结果是相互重叠的少量聚簇。
阶段2此阶段的主要任务是对所有聚簇的交叉部分进行处理,将交叉点归类。这一阶段的MapReduce化主要体现在对交叉集的处理上:在获取所有交叉集合的信息后,将这些交叉集分布到不同的平台上采用最近邻优先吸收聚类算法进行处理;然后将这些信息汇总,得到总的聚类结果。
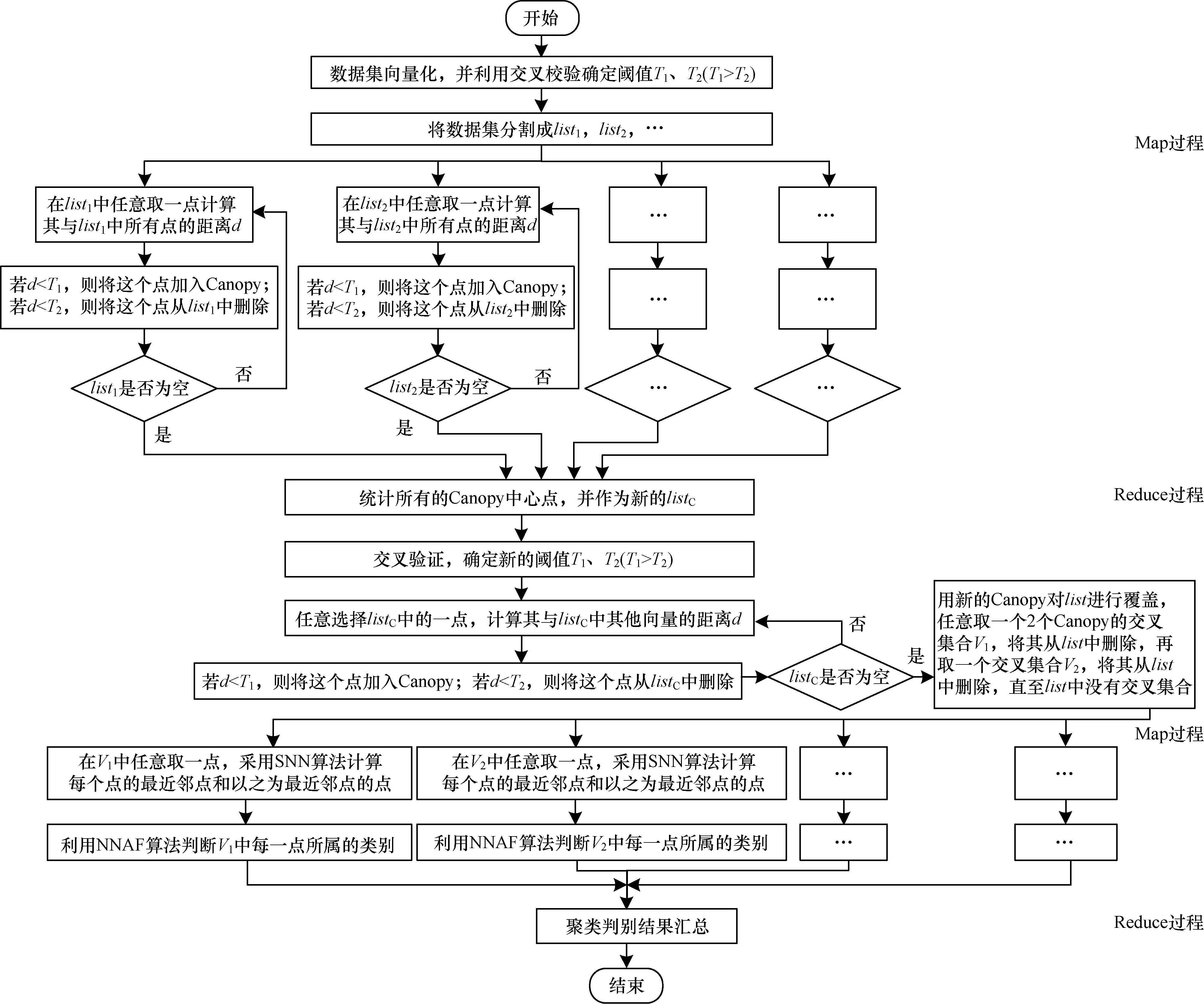
图2 改进的最近邻优先吸收聚类算法结构
3 实验
3.1 实验数据来源和平台
实验的数据集来源于UC Irvine Machine Learning Repository数据库。该数据库是一个2008年出现的包括多个数据集在内的词汇数据集集合,本文采用其中3个大小区分明显的数据集:
1)Enron Emails数据集,大小约为50 MB,包括39 861封邮件、28 102个单词,总单词数约为6 400 000个。
2)纽约时报新闻文章数据集,大小约为900 MB,包括300 000篇文章、102 660个单词,总词数约为100 000 000个。
3)PubMed摘要数据集,在Linux系统下压缩包大小为7 GB,包括8.2×106条摘要、141 043个单词,总词数约为7.3×108个。
所有实验均在Hadoop平台完成,实验平台的配置为:双核2.6 GHz CPU;4 GB内存;30 GB硬盘;操作系统为Centos6.3;JDK为1.7.0_45;Hadoop版本为Hadoop-0.2-0.2。
3.2 实验步骤
Job1:多次使用Canopy算法产生k个Canopy中心。
Job2:利用k个中心生成k个相互重叠的聚簇。
Job3:对于重叠部分采用改进的最近邻优先聚类算法判断重叠部分的数据归属。
Job4:整理归并,输出最终结果。
3.3 实验难点及解决方法
在实验过程中,存在一些的难点,其内容以及解决方法如下:
1)实验数据集的属性过多,必须进行降维处理,否则将会出现维度灾难并严重影响聚类效率。因此,采用高相关滤波和随机森林相结合的降维方法对属性进行处理。
2)对数据集进行分析,获取用于比较算法效果的最近邻优先吸收聚类算法的距离阈值和数量阈值。由于数据集的规模过大,属性过多,在设置2个阈值时需要进行大量的调整。但是在改进方法中,只需计算2个相交的Canopy的距离阈值和数量阈值。
3)聚类的数量的控制。在大规模数据集中采用Canopy算法得到的粗聚类的Canopy数较多,需要进行多重Canopy聚类。
4)均方误差的计算。由于数据集的规模过大,在计算均方误差时,很容易出现卡死的现象,因此分别针对每一个聚类结果采用分布式来对其进行计算,并将结果进行汇总,求取均值,得到整体聚类的均方误差来衡量聚类效果。
3.4 实验结果分析
为考察本文算法的聚类结果的质量,采用改进后的最近邻优先吸收聚类算法分别针对上述3种规模不同的数据集进行处理,并将其与Mahout算法库中的代表性聚类算法K-means算法和MapReduce框架下的最近邻优先吸收聚类算法进行比较,结果分别如表1~表3所示。由于算法的数据集规模过大,无法进行预聚类,因此无法对准确率进行精确衡量,只能用均方误差代替。
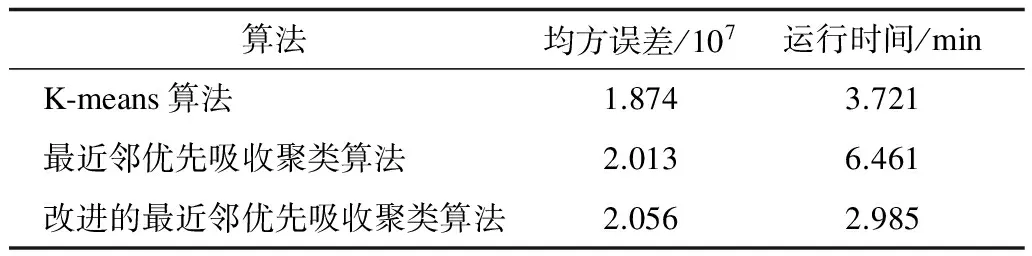
表1 Enron Emails数据集实验结果比较
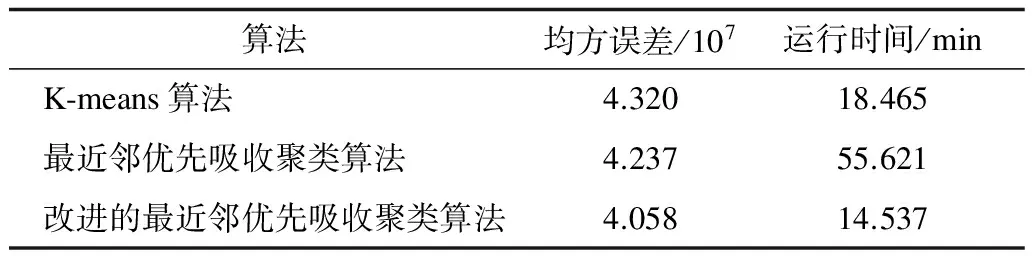
表2 纽约时报新闻文章数据集实验结果比较
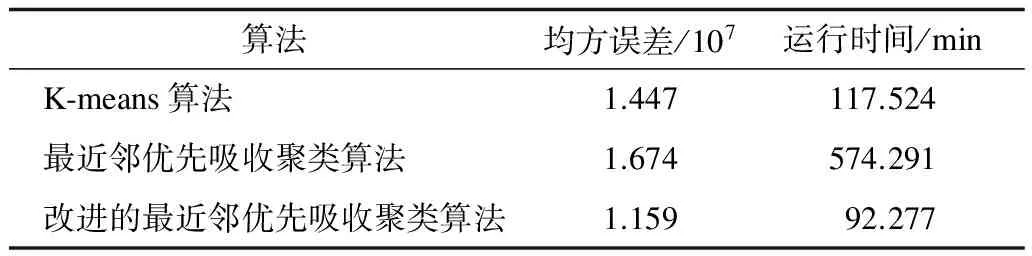
表3 PubMed摘要数据集实验结果比较
由表1~表3中的数据可以看出,在采用Canopy算法对最近邻优先算法改进后,运行时间相对未改进的最近邻优先算法有了很大的提升,尤其是在数据规模更大的情况下,提升更为明显。在较小的Enron Emails数据集中,改进的最近邻优先吸收聚类算法的运行时间比最近邻优先吸收聚类算法提高了116.45%;但是在较大的PubMed摘要数据集中,提高了522.36%。而衡量聚类准确率的均方误差在数据规模不大的情况下,区别并不是很大,在规模较小的Enron Emails数据集中,改进的最近邻优先吸收聚类算法的均方误差比起最近邻优先吸收聚类算法高了2.14%,差别较低。但是当数据集规模逐渐变大时,改进的最近邻优先聚类算法的准确率还是会保持在一定的水平。而最近邻优先聚类算法由于阈值设置的问题,在数据集规模扩大的情况下,会更容易出现准确率下降的问题。如表2、表3所示,在规模处于中等的纽约时报新闻文章数据集中,改进的最近邻优先吸收聚类算法的均方误差比起最近邻优先吸收聚类算法要低4.41%;在规模较大的PubMed摘要数据集中,改进的最近邻优先吸收聚类算法的均方误差比起最近邻优先吸收聚类算法要低44.43%,聚类效果更优。
与Mahout算法库中的K-means算法相比,改进的最近邻优先吸收算法在运行速度上更占优势,提升幅度约为27%。在均方误差的比较上,数据集较小的情况下,K-means算法的均方误差较小,聚类效果更好,约为10%。但是随着数据集规模的增加,K-means算法受局部最优的影响,其均方误差比起改进的最近邻优先吸收聚类算法更大,准确率更低。在数据规模中等的纽约时报新闻文章数据集中,改进的最近邻优先吸收聚类算法的均方误差要比K-means算法低6.46%,在数据集规模极大的PubMed摘要数据集中,改进的最近邻优先吸收聚类算法的均方误差要比K-means算法低24.85%。
为更直观地显示不同算法在不同规模数据集上的效果,本文进行了趋势图比较。不同算法在不同规模数据集上的运行时间如图3所示。
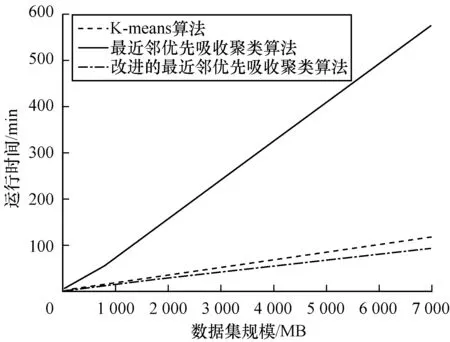
图3 3种算法的运行时间比较
不同算法针对不同规模数据集的均方误差如图4所示。可以看出,在数据集规模不断变大的情况下,3种算法的运行时间和聚类效果的变化情况。最近邻优先吸收聚类算法的运行时间受数据集规模的影响最大,随着数据集规模的增长,最近邻优先吸收聚类算法的运行时间比起另外2种算法,变化幅度最为明显。这主要是因为数据集变大后采用SNN算法来计算所有向量之间的距离所需的时间大量增加。而K-means算法和改进的最近邻优先吸收聚类算法的运行时间虽然也有增加,但仍在正常的范围内。

图4 3种算法的均方误差比较
随着数据集规模的增长,均方误差上升,最近邻优先吸收算法的聚类效果下降最为严重,这是因为数据集规模的增加会使阈值的影响不断变大,造成聚类效果的下降。其次是K-means算法,局部最优现象也会造成聚类效果的下降。综上所述,在处理大规模数据集时,改进的最近邻优先吸收聚类算法性能更优。
4 结束语
本文借助Canopy算法提出基于MapReduce的改进最近邻优先吸收聚类算法,并将其应用于海量数据处理平台。实验结果表明,本文算法可在快速处理大规模数据集的同时保持较好的聚类效果。下一步将从提高运行速率和准确率的角度出发对算法进行优化,以期在改善聚类效果的同时提高聚类效率。
[1] 牛新征,佘 堃.面向大规模数据的快速并行聚类划分算法研究[J].计算机科学,2012,39(1):134-137.
[2] 陈东明,刘 健,王冬琦,等.基于MapReduce的分布式网络数据聚类算法[J].计算机工程,2013,39(7):76-82.
[3] JI Yanqing,TIAN Yun,SHEN Fangyang,et al.Leveraging MapReduce to efficiently extract associations between biomedical concepts from large text data[J].Micro-processors and Microsystems,2016,46(B):202-210.
[4] PULGAR-RUBIO F,RIVERA-RIVAS A J,PÉREZ-GODOY M D,et al.MEFASD-BD:multi-objective evolutionary fuzzy algorithm for subgroup discovery in big data environments-a MapReduce solution[J].Knowledge-Based Systems,2017,117(1):70-78.
[5] TSAI C F,LIN W C,KE S W.Big data mining with parallel computing:a comparison of distributed and MapReduce methodologies[J].The Journal of Systems and Software,2016,122(1):83-92.
[6] 冯丽娜.并行K-means聚类方法在简历数据中的应用研究[J].计算机科学,2009,36(8):276-279.
[7] 谢娟英,王艳娥.最小方差优化初始聚类中心的K-means算法[J].计算机工程,2014,40(8):205-211,223.
[8] SHAHRIVARI S,JALILI S.Single-pass and linear-time K-means clustering based on MapReduce[J].Information Systems,2016,60(C):1-12.
[9] 冀素琴,石洪波.基于MapReduce的K-means聚类集成[J].计算机工程,2013,39(9):84-87.
[10] 赵 庆.基于Hadoop平台下的Canopy-Kmeans高效算法[J].电子科技,2014,2(7):29-31.
[11] 胡建军,唐常杰,李 川,等.基于最近邻优先的高效聚类算法[J].四川大学学报(工程科学版),2004,6(4):93-99.
[12] 王 鑫,王洪国,张建喜,等.基于数据分区的最近邻优先聚类算法[J].计算机科学,2005,12(9):188-190.
[13] 程 苗,陈华平.基于Hadoop的Web日志挖掘[J].计算机工程,2011,41(11):37-39.
[14] SANDEEP P,MORGAN F,CAWLEY S,et al.Modular neural tile architecture for compact embedded hardware spiking neural network[J].Neural Processing Letters,2013,38(2):131-153.
[15] 冀素琴,石洪波.面向海量数据的K-means聚类优化算法[J].计算机工程与应用,2014,14(1):143-147.
