基于DWT的多模型组合社交网站访问量预测

王少帅 宋礼鹏

(中北大学大数据学院 太原 030051)

(1019844335@qq.com)

随着互联网的蓬勃发展,社交网站逐渐发展成为人们主要交流工具之一.蠕虫病毒作为一种通过网络传播的计算机病毒,可借助社交网站使得其在短时间内快速蔓延,给互联网带来严重威胁.通过对目标局域网内社交网站访问量分析建模,预测未来各个时段的社交网站访问量,并结合其他信息在不同时段加以不同的干预手段,从而有效地预防或者抑制蠕虫病毒的传播.

网络流量预测作为一个经典的时间序列预测问题,一直为国内外研究者所研究.按照建模方法可将其划分为以ARMA(auto-regressive and moving average model)[1]、ARIMA(autoregressive integrated moving average model)[2-3]、指数平滑法[4]等为代表的线性时间序列模型和以GBDT(gradient boosting decision tree)、神经网络、SVM(support vector machine)[5-8]等为代表的非线性建模方法两大类.网络流量变化的混沌特性,决定了网络流量时间序列的非线性,这导致了线性时间序列模型预测往往难以达到预期的预测效果.而传统的非线性网络流量预测模型又存在预测结果不稳定,易发生“过拟合”的现象.针对这个问题,李振刚[9]首次将高斯过程回归模型引入网络流量预测,提高了网络流量预测精度.

本文针对局域网中网络流量的社交网站访问量进行分析与预测.局域网中社交网站访问量相对于总体网络流量而言,其序列变化的不确定性更大,因而比传统网络流量更加难以预测.Sudheer等人[10]将离散小波变换(DWT)应用于电网的短期负荷预测中,将短期负荷时间序列分解成稳定部分(周期分量)与不确定性部分(残余分量),并分别使用针对性模型进行预测.本文将该方法引入局域网社交网站访问量的预测中,并针对周期分量使用高斯过程回归模型(GPR)[11-13]进行预测,同时对残余分量使用加权近邻模型(WNN)[14]进行预测,提出一种基于DWT的高斯过程回归与WNN组合预测模型.

为验证模型预测效果,本文采用均方根误差RMSE(root mean square error)作为评价指标,并与其他模型进行对比.

1 高斯过程原理

高斯过程回归是基于贝叶斯网络的一种机器学习算法,它既具有贝叶斯网络的推理能力,同时还具备SVM处理小样本、非线性、高维度的问题的自适应能力.它直接从函数空间角度出发,定义一个高斯过程来描述函数分布,并在函数空间进行贝叶斯推理.

由于观测通常是带噪声的,因而可假设模型为

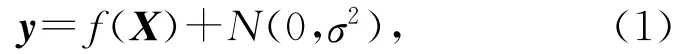
其中函数f(X)被假设给予一个高斯过程先验,即

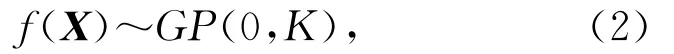
其中K为协方差函数.

对于新测试输入x*,根据高斯过程的性质及测试数据与训练数据来源于同一分布的特点,可以得到观测值y(训练样本输入)和预测值y*(测试样本输出)的联合先验分布

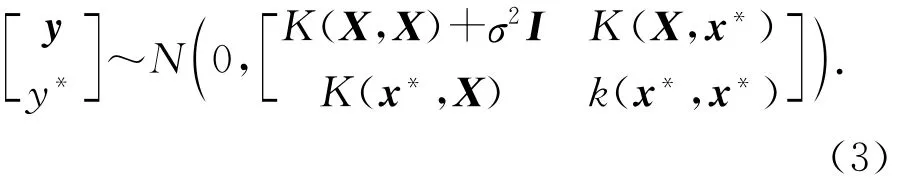
由式(3),结合贝叶斯估计原理和联合正态分布的条件概率性质,可得预测值y*(测试样本输出)的后验分布:

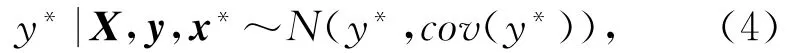
即可求得预测值y*的分布函数.与cov(y*)的表达式如下:

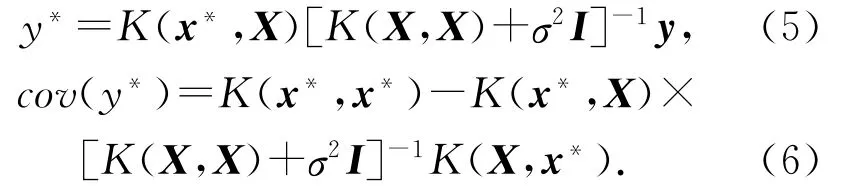
2 加权近邻模型

加权近邻模型(WNN)是基于K-最近邻算法的改进[14].其主要思想是将时间序列按其周期分段后,可得到矩阵

其中,L n为最近周期.进一步利用计算得到L n与其他周期的距离,并按降序排序得到距离的集合q={q1,q2,…,qk},其中q1表示最远距离,qk表示最近距离.

最终预测未来L n+1的预测公式为

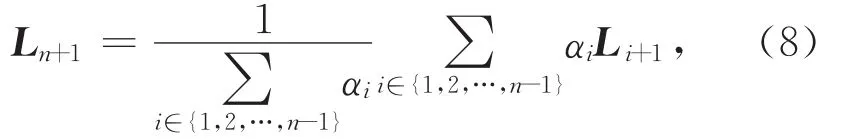
3 模型的提出

局域网内社交网站访问量变化的不确定性,给其预测带来了极大的困难.针对这个问题,本文尝试使用离散小波变换(DWT)将时间序列分解成周期分量(低频部分)与残余分量(高频部分),并分别使用多时间粒度特征的高斯过程回归模型(GPR)和加权近邻模型(WNN)进行针对性预测.即使用离散小波变换(DWT)将时间序列的稳定部分和不确定性部分分解出来,并进行针对性预测,进而减小由于时间序列不确定性对预测带来的影响,提高了预测精度.具体过程如图1所示:

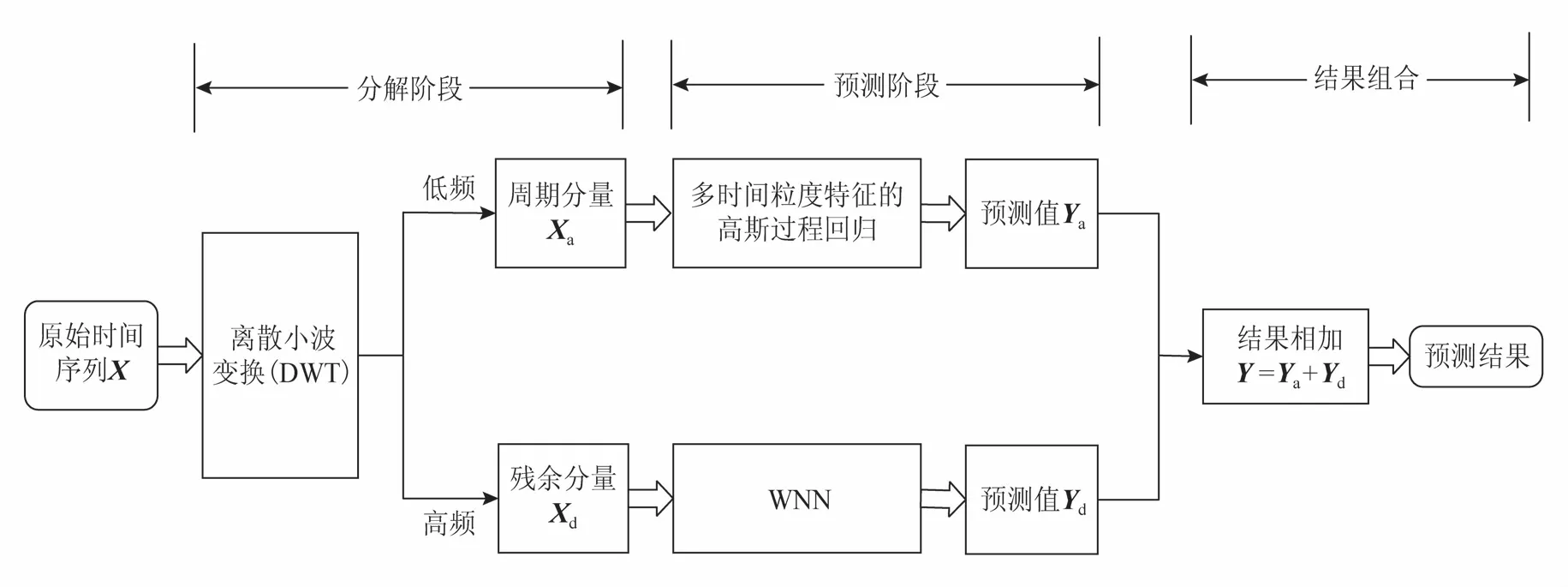
图1 组合预测模型流程图

由图1可知,模型预测步骤可分为3步,下面将分别描述.

3.1 分解阶段

时间序列从结构上看,可拆分成2部分:一部分是周期分量,该分量包含原始序列的总体变化规律;另一部分是残余分量,该分量体现了原始序列的细节性变化规律.

本文尝试使用DWT对时间序列进行拆分,采用的小波为daubechies的8个系数的最小不对称小波.DWT可设置分解的层数level来决定对时间序列数据分解程度.若层数level设置过低,会导致DWT不能完全将时间序列中的不确定性部分分解出来;若层数level设置过高,则会导致DWT将时间序列中的一部分周期分量误认为是不确定性的,进而归为残余分量.本文通过设置level=3,得到网络流量时间序列的低频部分,根据低频部分进行重构,得到周期分量Xa,该分量序列反映原序列的大致趋势和走向.进一步,通过原始序列X减去周期分量Xa得到残余分量Xd,即Xd=X-Xa,残余分量序列包含原始序列细节性变化.

3.2 预测阶段

3.2.1 周期分量X a预测

针对反映原始序列总体变化规律的周期分量Xa,考虑到传统网络流量预测模型,往往只考虑单个时间粒度的信息对未来预测结果的影响,并未充分利用多个时间粒度的信息进行预测.本文从多时间粒度的角度出发,通过选取不同的时间步长统计出不同的网络流量时间序列,并取前N天的网络流量时间序列充当特征,构成多时间粒度特征,同时结合高斯过程回归模型,对其进行预测.

3.2.2 残余分量X d预测

针对反映原始序列细节性变化规律的残余分量,可认为原始时间序列的不确定性部分均被分解到该分量内,从而采用更加简单的WNN进行预测.

3.3 结果组合

使用多时间粒度特征的高斯过程回归模型对周期分量Xa进行预测,得到预测结果Ya,代表未来时间序列的总体变化规律.使用WNN对残余分量Xd进行预测,得到预测结果Yd,代表未来时间序列的细节波动.将2个结果相加,得最终预测结果,即Y=Ya+Yb.

4 实验仿真

为验证本模型的预测效果,我们收集并统计得出中北大学局域网内包括QQ空间、QQ邮箱、豆瓣网、人人网、腾讯微博、新浪微博6个社交网站的访问量充当仿真数据.由于各大社交网站1天24 h内除8:00—22:00(包括8:00和22:00)有较高的访问量之外,其他时间访问量均接近0.因此我们以未来1天的8:00—22:00(包括8:00和22:00)的访问量为预测目标,使用本模型进行预测,并与指数平滑法、支持向量机(SVM)的预测结果进行对比,如图2所示:

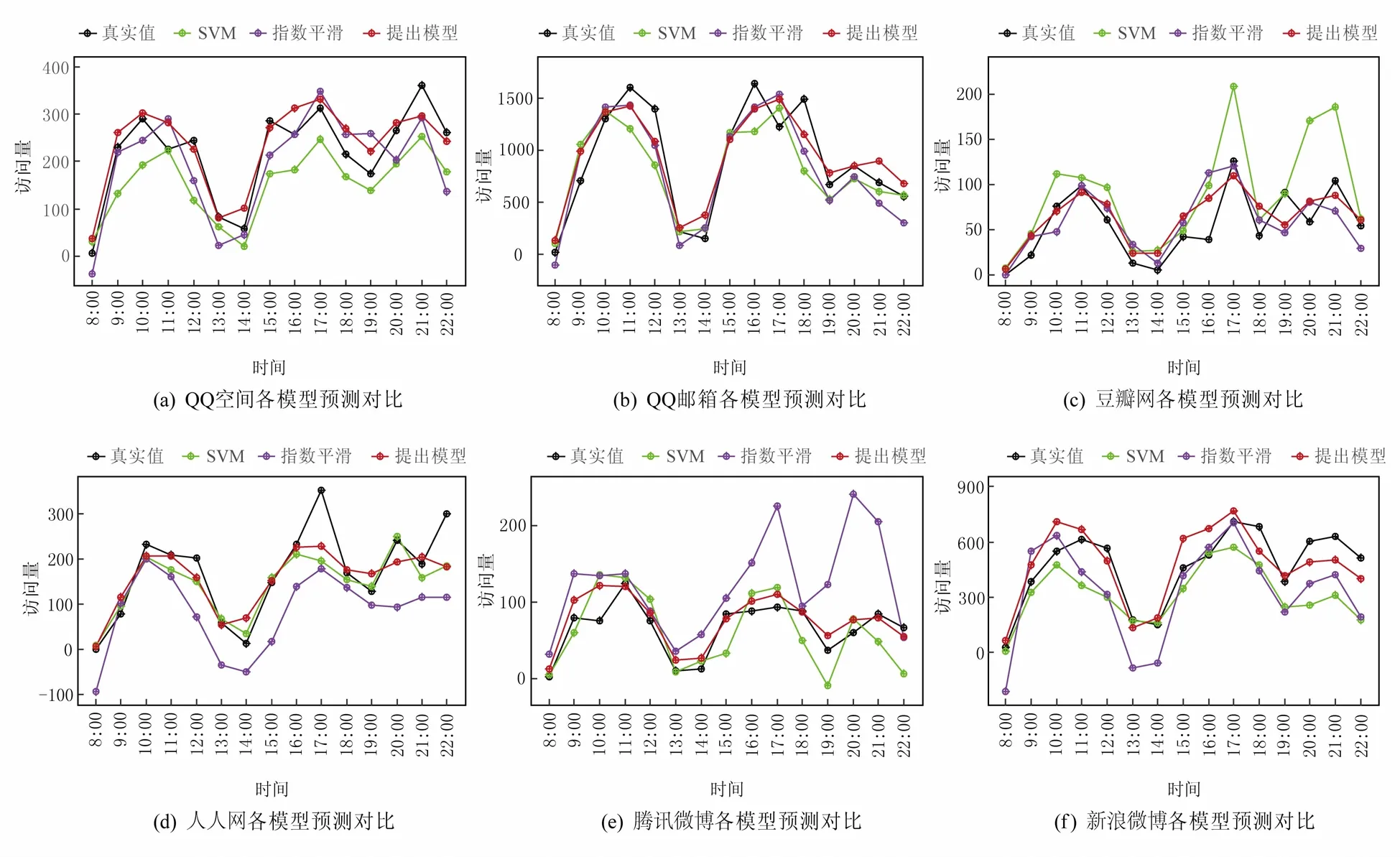
图2 社交网站访问量预测对比图

由图2可直观观察到,本模型的预测结果更接近真实值.为进一步验证模型预测效果,本文采用均方根误差RMSE作为评价指标,计算公式如式(9)所示:

其中,n为数据集的数目,Xt为真实值,X^t为预测值.通过式(9)计算,得到各大社交网站预测的均方根误差RMSE如表1所示.其中,总均方根误差是首先将QQ空间、QQ邮箱、豆瓣网、人人网、腾讯微博以及新浪微博的预测结果合并,再通过式(9)计算而得.

表1 均方根误差RMSE对比表

由表1可知,本模型在QQ空间、QQ邮箱、豆瓣网、人人网、腾讯微博和新浪微博的数据集上,其均方根误差RMSE均低于其他2个模型,其总均方根误差更是远低于其他2个模型.

5 结 论

社交网站访问量时间序列的混沌性,决定了社交网站访问量变化的不确定性,导致其访问量预测成为一个难题.本文从时间序列可分解的角度出发,利用离散小波变换(DWT),将该时间序列分解成反映序列总体变化规律的周期分量与体现了序列细节性变化规律的残余分量2部分.针对周期分量,本文构造出多时间粒度特征并结合高斯过程回归模型(GPR)进行预测;针对残余分量,本文使用更为简单的近邻加权模型(WNN)进行预测,然后将结果合并得到最终预测结果.为验证模型优劣,我们将收集得到的中北大学局域网内QQ空间、QQ邮箱、豆瓣网、人人网、腾讯微博和新浪微博这6个数据集分别进行仿真实验,并使用均方根误差RMSE作为评价指标,将本模型、支持向量机(SVM)和指数平滑这3个模型进行对比,结果表明,本模型预测结果最优.

本文对网络流量中的局域网内社交网站访问量进行分析与预测,并基于离散小波变换(DWT)将时间序列进行分解,同时结合高斯过程回归模型(GPR)和近邻加权模型(WNN)进行组合预测,预测精度相对其他模型有了进一步提升,对局域网内网络安全的分析与预防具有重要参考价值.

[1]何书元.应用时间序列分析[M].北京:北京大学出版社,2003:87-89

[2]Box G E P,Jenkins G M,Reinsel G C.Time Series Analysis Forecasting and Control[M].3rd ed.New York:Prentice-Hall,2007:25-271

[3]Schoukens J,Pintelon R.Identigication of Linear Systems:A Practical Guideline to Accurate Modeling[M].Oxford:Pergamon,1991:68-70

[4]Szmit M,Szmit A.Use of holt-winters method in the analysis of network traffic:Case study[J].Communications in Computer&Information Science,2011,160:224-231

[5]Liao Q,Yao J,Yuan S.SVM approach for predicting LogP[J].Plant Foods for Human Nutrition,2006,10(3):301-309

[6]Kachoosangi F T.How reliable are ANN,ANFIS,and SVM techniques for predicting longitudinal dispersion coefficient in natural rivers[J].Journal of Hydraulic Engineering,2016,142(1):1-8

[7]Hossain M M,Miah M S.Evaluation of different SVM kernels for predicting customer churn[C]//Proc of Int Conf on Computer&Information Technology.Piscataway,NJ:IEEE,2016:1-4

[8]Che N,Murphree D H,Upadhyaya S,et al.Multitask LS-SVM for predicting bleeding and re-operation due to bleeding[C]//Proc of IEEE Int Conf on Healthcare Informatics.Piscataway,NJ:IEEE,2017:56-65

[9]李振刚.基于高斯过程回归的网络流量预测模型[J].计算机应用,2014,34(5):1251-1254

[10]Sudheer G,Suseelatha A.Short term load forecasting using wavelet transform combined with Holt-Winters and weighted nearest neighbor models[J].International Journal of Electrical Power&Energy Systems,2015,64(64):340-346

[11]Seeger M.Gaussian processes for machine learning[J].International Journal of Neural Systems,2004,14(2):69-106

[12]何志昆,刘光斌,赵曦晶,等.高斯过程回归方法综述[J].控制与决策,2013,28(8):1121-1129

[13]He Zhikun,Liu Guangbin,Zhao Xijing,et al.Temperature model for FOG zero-bias using Gaussian process regression[G]//AISC 180:Intelligence Computation and Evolutionary Computation.Berlin:Springer,2013:37-45

[14]Lora A T,Santos J M R,Exposito A G,et al.Electricity market price forecasting based on weighted nearest neighbors techniques[J].IEEE Trans on Power Systems,2007,22(3):1294-1301