基于多策略差分布谷鸟算法的粒子滤波方法

黄　辰　费继友,　王丽颖　刘晓东

(1.大连交通大学机械工程学院， 大连 116028； 2.大连交通大学动车运用与维护工程学院， 大连 116028)

0　引言

近年来，粒子滤波技术被广泛应用于处理实际工程问题[1-2]。例如：目标跟踪[3-5]、故障检测[6-7]、状态估计[8]、定位导航[9-12]以及图像处理[13]等领域。粒子滤波的思想[14]源于蒙特卡洛利用一组加权随机粒子来表示概率分布，借助实际测量值来调整各个粒子权值和位置来近似获得实际概率分布。因此，粒子滤波能有效克服扩展卡尔曼滤波在处理高度非线性问题时估计精度急剧下降的缺点。

虽然粒子滤波能解决对模型的非线性和非高斯的约束问题，但算法本身仍存在一些缺陷[15-17]。随着算法运行，粒子的权值方差会出现递增，将出现严重的粒子退化现象。为缓解退化问题，GORDON等[18]引入了舍弃小权值粒子的重采样方法。但由于在重采样过程中对大权值粒子的多次复制，减弱了粒子多样性，造成粒子贫化现象。近期，采用群体智能来优化粒子滤波算法[19-20]，将生物机制引导的优化理论嵌入粒子滤波算法框架是现代粒子滤波领域中一个崭新的发展方向。HAN等[21]提出将布谷鸟算法与粒子滤波算法相结合，并成功应用于故障检测中，具有较好的鲁棒性。

本文提出一种基于改进布谷鸟算法的粒子滤波方法(Particle filter based on improved cuckoo search, ICS-PF)。一方面，在Levy飞行过程中引入多策略差分变异来增加算法的多样性；另一方面，在新解的选择机制上采用排队优选与贪心算法相结合来提高选择效率，并将改进的布谷鸟算法用来优化粒子滤波。

1　粒子滤波算法基本原理

假设非线性系统的状态空间模型[22]，即状态方程和观测方程为

(1)

式中xk——系统k时刻的状态变量

yk——系统k时刻的测量值

f——系统的状态转移函数

h——系统的观测函数

uk-1——系统的过程噪声

vk——测量噪声

(2)

其中

Yk={y1,y2,…,yk}

式中Yk——1～k时刻的观测信息

δ——狄拉克(Dirac-delta)函数

粒子滤波采用样本均值来代替积分运算，能够获得状态变量最小方差估计。当样本(粒子)数量达到足够大时，可以逼近真实的概率密度分布。

(3)

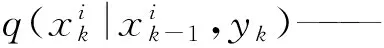
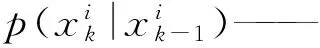
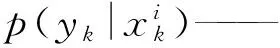
在标准粒子滤波算法中，重要密度函数取状态转移概率密度，即

(4)

将式(4)代入式(3)得

(5)

粒子滤波的状态输出估计可表示为

(6)

2　多策略差分布谷鸟算法的粒子滤波

2.1　标准布谷鸟算法

布谷鸟算法是新型有效的群体智能算法，根据模拟寄生育雏繁殖后代过程演化而来。布谷鸟种群将挑选合适的其他种群鸟类为其孵化产卵，所选择的鸟巢中通常有宿主刚产下的蛋，以此来降低被发现的概率。一旦宿主发现鸟巢中存在寄生卵将会丢弃外来的蛋或再重新构建新的鸟巢。标准的布谷鸟算法需要遵循3条理想规则[23-25]：

(1)布谷鸟 1 次只产1个卵，并随机选择鸟巢进行孵化。

(2)当前所有鸟巢中位置最好的鸟巢将会被保留到下一代。

(3)可用的寄生鸟巢数是固定的，且宿主发现鸟巢中布谷鸟蛋的概率是pa，pa∈[0,1]。

在优化实际问题时，用一个含有D维向量的鸟巢位置来表示搜索空间中的一个候选解。 在当前解的基础上，通过Lévy Flight随机游动搜索下一代鸟巢位置。将每个鸟巢位置代入目标函数中将会得到相对应的一个适应度f(x)，根据f(x)来判断当前鸟巢位置的优劣。然后，按发现概率舍弃部分解并由偏好随机游动搜索策略重新生成与丢弃解相同数量的新解。根据贪婪准则来保留较好的解以完成一次迭代。

布谷鸟算法首先采用Lévy Flight的随机游动搜索策略来搜索新鸟巢位置，其更新公式

(7)

其中

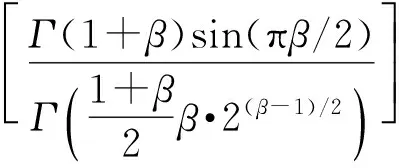
(8)

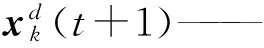
u、v——服从标准正态分布的2个随机数

c1——步长调节因子，通常c1取0.01

β——常数

Γ——标准的Gamma函数

gd——当前最优鸟巢的第d维向量

在通过Lévy Flight的随机游动搜索获得的新鸟巢位置中，需要根据发现概率pa，按照偏好随机游动搜索策略来产生新解。偏好随机游动更新为

(9)

式中r——0～1范围内的随机数

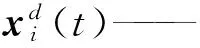
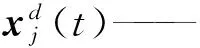
2.2　多策略差分进化布谷鸟算法

在标准布谷鸟算法中，首先采用Lévy Flight的随机游动搜索，然后按发现概率通过偏好随机游动搜索来舍弃部分鸟巢。为提高搜索效率，采取预先设定的比例同时进行Lévy Flight随机游动搜索和偏好随机游动搜索的策略。

布谷鸟算法的偏好随机游动搜索策略是采用式(9)中2个随机解的差异来更新一部分Lévy Flight的随机游动搜索新鸟巢位置的解。考虑到搜索策略的多样性，将多策略差分变异操作引入布谷鸟算法的偏好随机游动搜索过程中。由3种差分策略和原来的偏好随机游动共4个搜索策略共同构成新的偏好随机游动搜索策略。

在每次迭代中，差分算法的每个染色体都会通过变异操作来产生新的染色体，常用的变异策略[26-28]为

Rand/1

vi,g=xr1,g+F(xr2，g-xr3，g)

(10)

Best/1

vi,g=xbest,g+F(xr1，g-xr2，g)

(11)

Rand/2

vi,g=xr1,g+F(xr2，g-xr3，g)+F(xr4，g-xr5，g)

(12)

Current-to-best/1

vi,g=xi,g+F(xbest,g-xi,g)+F(xr1，g-xr2，g)

(13)

Current-to-rand/1

vi,g=xi,g+r(xr1,g-xi,g)+F(xr2，g-xr3，g)

(14)

式中F——缩放比例因子

r1～r5——[1,NP]中的随机整数且与i不等

vi,g——经过变异后第g代第i个染色体

xr1,g～xr5,g——第g代5个不相同的染色体

xbest,g——当前群体中的最好染色体

xi,g——变异前第g代第i个染色体

由于Lévy Flight随机游动搜索过程中已经将当前的全局最优解代入，因此，可以采用式(10)、(12)和式(14)的策略。多策略的偏好随机游动搜索过程包括4个选择，即式(9)、(10)、(12)、(14)。在偏好随机游动搜索过程中，针对不同的优化问题，不同策略发挥的作用也有所不同。因此，为加快搜索效率引入选择因子并结合轮盘赌机制来调整4个候选的偏好随机游动搜索各个策略被选择的可能性。

当布谷鸟算法中有新解产生时，采用贪婪算法来决定新解是否可以代替旧解。贪婪算法是以每个鸟巢的位置为基准，用新产生具有更优的适应度个体来替换上一代，与其它鸟巢之间没有相互交流。如此舍弃的鸟巢位置的适应度可能与某些鸟巢位置的适应度相比是优秀的，从而降低搜索的效率。因此，本文在选择新解的过程中，将贪婪与排队优选两种机制结合按照预先设定的比例来更新解。排队优选是将产生的与旧解不同的新解与全部旧解组成一个集合作为全集，根据各个解的适应度按照从优到劣进行排列，选出N个(定义的布谷鸟巢数)优选解作为新解集。

自适应差分变异布谷鸟算法的具体步骤如下：

(1)设定算法需要的参数和终止条件，并对种群进行初始化，计算每个个体的适应度值。

(2)针对每个鸟巢，根据已设定的Lévy Flight和偏好随机两种策略的选择比例c，通过与[0,1]间的随机数r进行比较，当r>c选择Lévy Flight随机游动搜索，否则选择偏好随机多策略游动搜索策略。

(3)当进入多策略偏好随机游动搜索策略，利用步骤(2)中的随机数r与每个策略的选择因子，选择4个策略所对应的右边界，分别为0.25(1-c)、0.5(1-c)、0.75(1-c)和1-c。

(15)

(4)按照优选和贪婪原则，由适应度来选择优秀个体进行迭代运算，用c1(c1∈(0,1))来调节2种选择机制的比例。随机产生1个随机数r1，当r1>c1时，采用贪婪原则；否则，采取排队优选原则。

(5)判断是否满足终止条件。满足则输出结果；否则，重复步骤(2)～(4)。

2.3　基于改进布谷鸟的粒子滤波

为克服原粒子滤波算法中存在的粒子贫化与退化问题，本文将基于多策略差分的布谷鸟算法引入到粒子滤波算法的重采样过程中。ICS-PF算法具体实现步骤如下：

(1)初始化。在初始时刻k=0时按照初始样本分布P(x0)进行采样，产生的N个粒子作为初始样本{xi(0)}(i=1,2，…,N)，xi(k)服从重要性密度函数。

xi(k)～q(xi(k)|xi(k-1),y(k))

(16)

(2)设置每个粒子的权重为wi=1/N。

(3)采用多策略差分布谷鸟算法来进化粒子，模拟布谷鸟优化算法的全局搜索行为:

①g=1，进入进化的初始粒子

{xg,i(k)}={xi(k)}(i=1,2,…,N)

(17)

② 将该粒子样本带入多策略差分布谷鸟算法中，按照多策略差分布谷鸟算法的步骤(2)～(5)进行相应的操作，得到进化后的新粒子集。在改进的布谷鸟算法中，所采用的适应度函数为

(18)

R——噪声方差

③ 将经过ICS-PF重采样后的粒子输出。

(4)利用式(5)计算新粒子的重要性权重并进行归一化处理，即

(19)

(5)重采样。可以舍弃权重低的粒子，并对权重高的粒子进行复制。

(6)粒子状态输出。求ICS-PF重采样后粒子的平均状态。

3　仿真

为验证算法ICS-PF的估计精度、运算时间和鲁棒性，采用单变量非静态增长模型对算法性能进行验证。此模型是研究各种PF算法性能时的常用模型，其状态方程和测量方程为：

状态方程

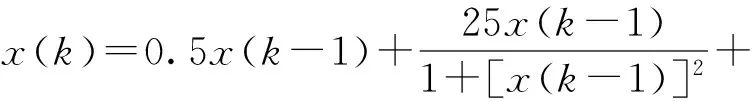
(20)

式中u(k)——状态方程中的零均值高斯噪声,方差为R

x(k)——系统k时刻的状态

测量方程

(21)

式中v(k)——测量方程中的零均值高斯噪声,方差为Q

y(k)——k时刻的观测量

仿真硬件环境为Intel i5处理器、主频2.40 GHz，4 GB内存，软件环境为Matlab 2014a。

3.1　精度测试

仿真采用粒子滤波算法(PF)、布谷鸟粒子滤波算法(CS-PF)、差分进化粒子滤波算法(DE-PF)与ICS-PF算法进行跟踪性能对比。定义一次独立仿真系统的估计误差为

(22)

式中T——进行一次仿真所用时间的总步数

xk——k时刻的状态真实值

实验中，ICS-PF和标准布谷鸟算法中设置发现概率pa=0.75，常数β=1.5。状态方程中的过程噪声和测量方程中的观测噪声的方差均为1，即R=1，Q=1。滤波初值x0=0.3，初始分布的方差p0=2，滤波步数k为50。随着粒子数量的增加，分别对PF、CS-PF、ICS-PF和DE-PF进行仿真。对每一种算法进行200次独立仿真的结果如表1所示。当粒子数N=20时，状态跟踪结果和误差曲线如图1、2所示。当粒子数N=50时，状态跟踪结果和误差曲线如图3、4所示。当粒子数N=100时，状态跟踪结果和误差曲线如图5、6所示。

由图1～7可知，与标准PF、DE-PF、CS-PF算法相比，ICS-PF对模型的真实状态具有更高的估计精度。ICS-PF算法是在多策略差分变异和CS的基础上进行全局搜索，由于搜索策略的增加能够有效提高粒子的多样性。同时，新引入的排队优选机制能够提高新解的质量，加快空间搜索效率。因此，提高了滤波的精度和速度。从表1可以看出，本文提出的ICS-PF算法在运算速度方面略快于DE-PF算法和CS-PF算法。而PF算法的运行时间最少，由于不用采用迭代操作来优化粒子目前的位置，算法相对简单。另外，由于ICS-PF算法省略变异操作，因此与CS-PF和DE-PF相比节省了时间。

表1　4种算法仿真结果对比Tab.1　Comparison of four algorithms simulation results

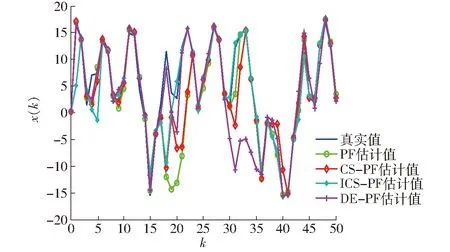
图1　滤波状态估计(N=20)Fig.1　State estimation of filter(N=20)

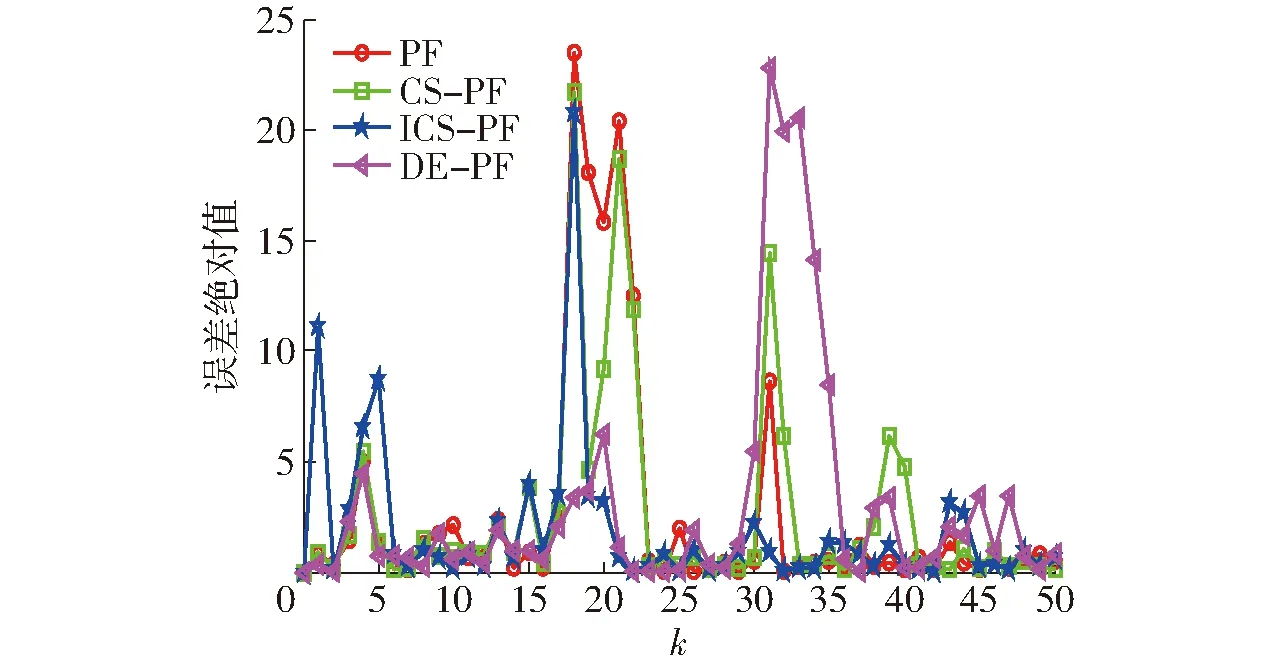
图2　状态误差绝对值(N=20)Fig.2　Absolute value of state error(N=20)

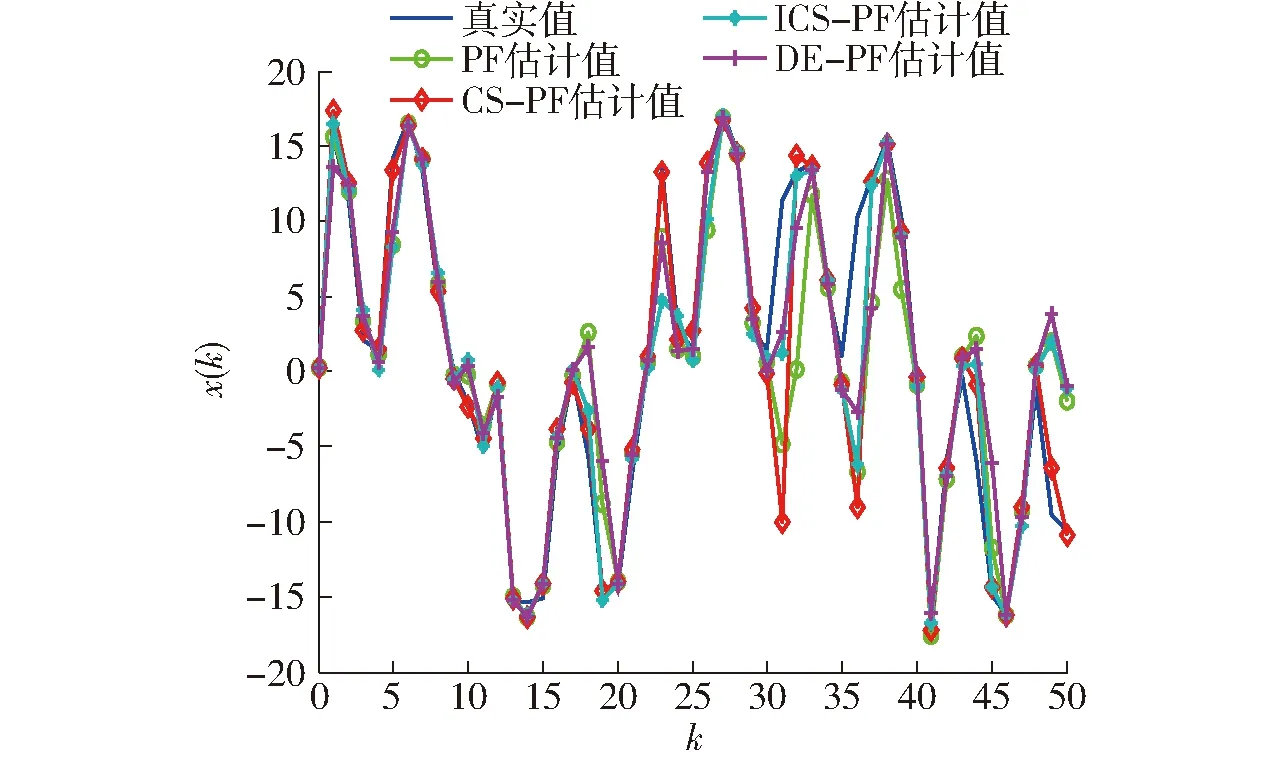
图3　滤波状态估计(N=50)Fig.3　State estimation of filter(N=50)

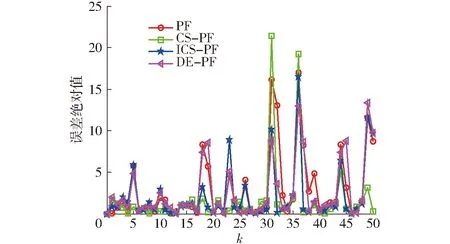
图4　状态误差绝对值(N=50)Fig.4　Absolute value of state error(N=50)

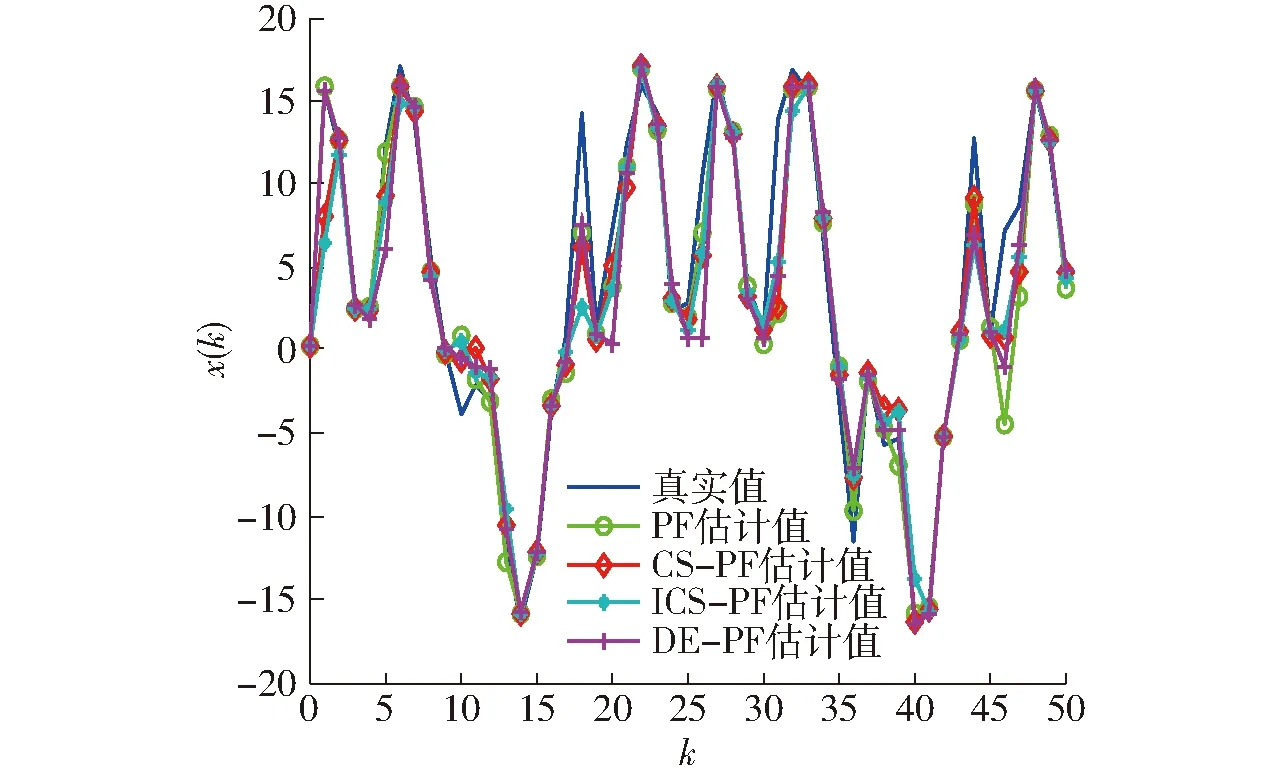
图5　滤波状态估计(N=100)Fig.5　State estimation of filter(N=100)

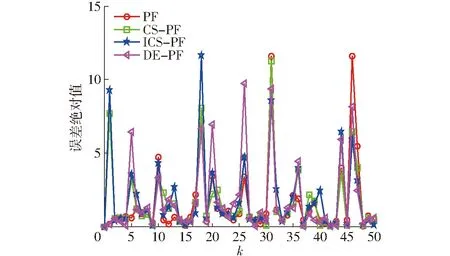
图6　状态误差绝对值(N=100)Fig.6　Absolute value of state error(N=100)

图7　粒子数对RMSE的影响Fig.7　Effect of particle amount on RMSE

由图7可以看出，当N增加时，这4种算法的滤波精度都有提高；在给定的相同噪声条件下，随着粒子个数从20增加到100，标准PF算法的滤波精度有大幅度提高，而ICS-PF的滤波精度变化相比较为平稳，且ICS-PF的滤波精度在粒子数为20时与标准PF算法粒子个数为100时的滤波精度相匹配。同样，其他两种智能优化粒子滤波算法在粒子个数较小时也具有较好的滤波性能。这是因为加入智能群体算法的粒子滤波能够借助群体的智能搜索来优化粒子的位置，使其分布更趋于合理。即使粒子数较少时仍能通过迭代寻优来增加粒子选择的多样性，使粒子能够在整个状态空间找到多个接近真实值的位置，保证重采样的选择结果趋于多样性，从而提高了估计精度，避免PF算法在粒子个数较少时容易出现由于多样性缺失而导致的重采样选择单一问题。因此，ICS-PF算法能够用少量的粒子来提高标准粒子滤波算法的稳定性和精度。

3.2　粒子多样性比较

为比较PF算法和ICS-PF算法的粒子多样性，选取PF算法和ICS-PF算法重采样后在N为20、50、100且k=30时，粒子在空间的状态如图8～10所示。

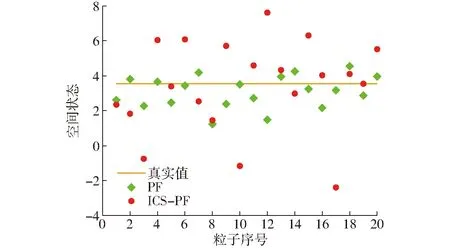
图8　粒子空间状态 (N=20)Fig.8　Particle space state (N=20)

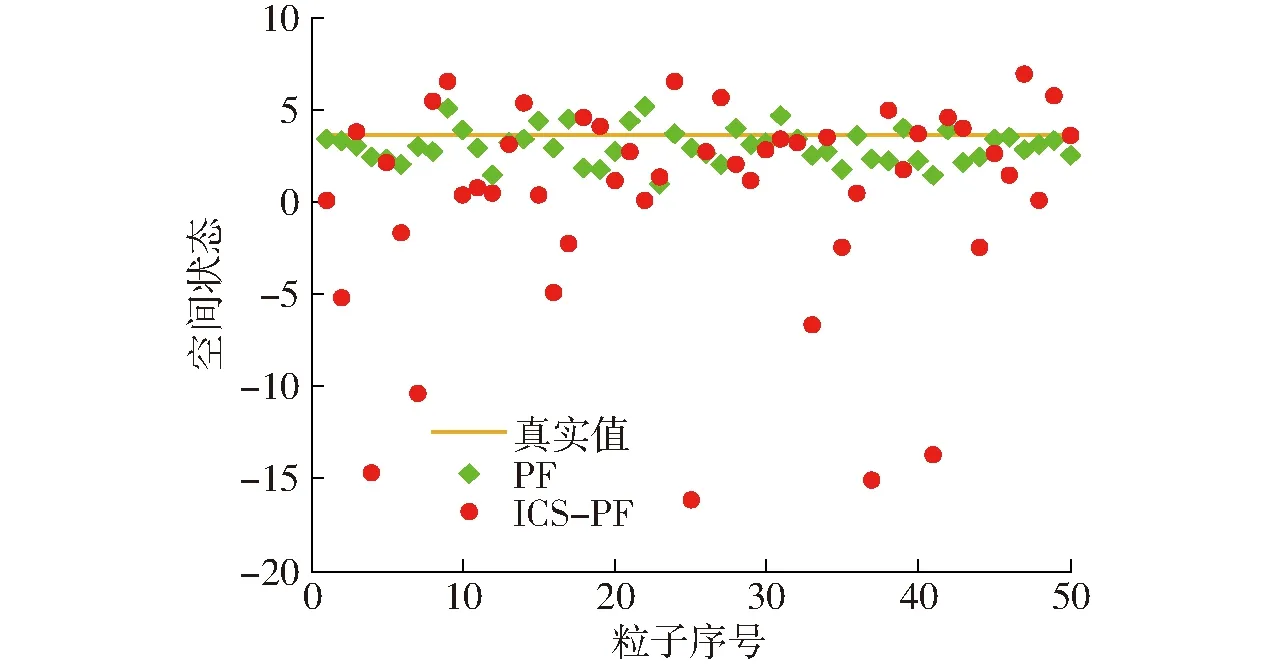
图9　粒子空间状态(N=50)Fig.9　Particle space state (N=50)

图10　粒子空间状态(N=100)Fig.10　Particle space state (N=100)

由图8～10可知，与标准 PF 算法的粒子多样性相比，ICS-PF在状态空间中具有更广泛的分布空间，多数粒子保持在高概率估计值附近，同时，低概率估计值仍有粒子分布，这样能够减少因粒子贫化而导致的高风险错误估计现象。

3.3　4种算法的粒子分布分析

为分析PF、CS-PF、ICS-PF和DE-PF 4种算法的粒子样本集与实际值关系，选取粒子个数N为50，过程噪声uk-1～N(0,1)，测量噪声vk～N(0,1)，仿真结果如图11～14所示。

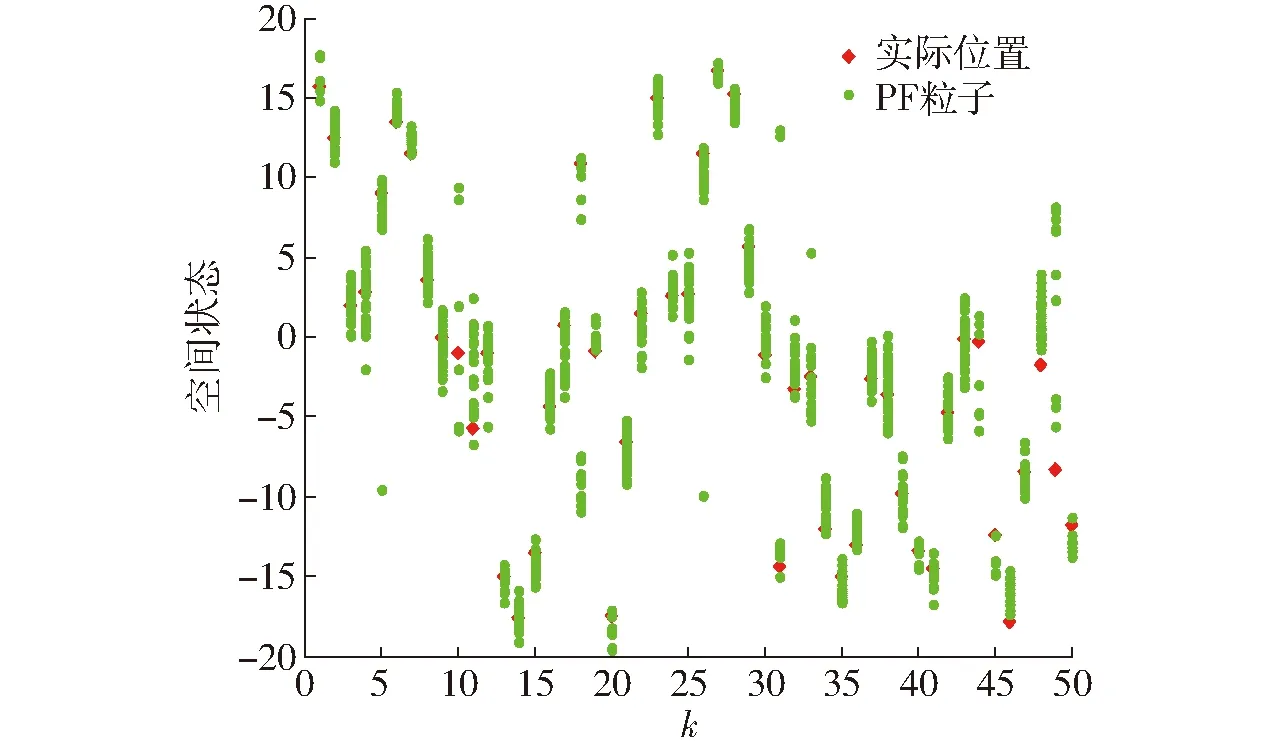
图11　PF重采样后的粒子分布Fig.11　Particle distribution of PF after resampling

图12　CS-PF重采样后的粒子分布Fig.12　Particle distribution of CS-PF after resampling

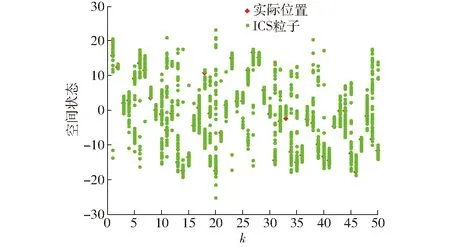
图13　ICS-PF重采样后的粒子分布Fig.13　Particle distribution of ICS-PF after resampling

从图11～14可以看出，4种算法中CS-PF重采样后的粒子空间分布范围最广，占据的空间面积最大，其次为ICS-PF算法。CS-PF在多样性性能方面是最优的，但分布太广会影响对最优粒子的判断，无法找到更接近真实值的粒子群体。标准PF算法在重采样后粒子分布过于集中，说明在重采样前粒子的权重相差较大，造成采样后粒子过于聚集。ICS-PF由于采用优选与贪婪相结合的新解选择机制，促使ICS-PF能更快找到合理的粒子分布。较好地平衡了多样性与寻优效率之间的关系。

4　结论

(1)布谷鸟算法是一种新型生物群启发算法，具有结构简单、控制参数少等优点，但存在易早熟、搜索速率不高等问题。为增加种群的多样性和搜索效率，引入多策略差分算法来改进布谷鸟算法中的偏好随机游动搜索策略，并采用轮盘赌原则对Lévy Flight随机策略和包含多个策略的偏好随机游动搜索之间进行选择。同时，采用排队优选和贪婪原则来选取新解，从而提高了布谷鸟群整体质量。

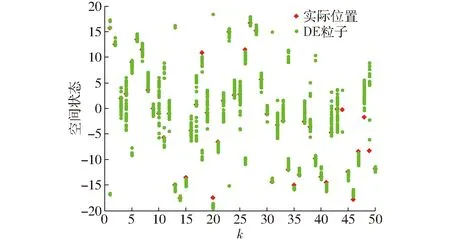
图14　DE-PF重采样后的粒子分布Fig.14　Particle distribution of DE-PF after resampling

(2)将改进的布谷鸟算法引入到粒子滤波中，来解决粒子滤波算法中的粒子贫化问题，使粒子模拟布谷鸟个体，在全局范围内搜索到更优的位置，促使粒子整体快速分布在真实值附近。仿真表明本文算法能够增加粒子的多样性，同时具有较高的鲁棒性和估计精度。

1夏楠, 邱天爽, 李景春,等. 一种卡尔曼滤波与粒子滤波相结合的非线性滤波算法[J]. 电子学报, 2013, 41(1):148-152.

XIA Nan, QIU Tianshuang, LI Jingchun, et al. A nonlinear filtering algorithm combining the Kalman filter and the particle filter[J]. Acta Electronica Sinica, 2013, 41(1):148-152. (in Chinese)

2左军毅, 张怡哲, 梁彦. 自适应不完全重采样粒子滤波器[J]. 自动化学报, 2012, 38(4):647-652.

ZUO Junyi, ZHANG Yizhe, LIANG Yan. Particle filter based on adaptive part resampling[J]. Acta Automatica Sinica, 2012, 38(4):647-652. (in Chinese)

3AHMED N, RUTTEN M, BESSELL T, et al. Detection and tracking using particle-filter-based wireless sensor networks[J]. IEEE Transactions on Mobile Computing, 2010, 9(9):1332-1345.

4刘凯, 梁晓庚, 李友年. 基于粒子滤波的非线性目标跟踪算法研究[J]. 四川兵工学报, 2014(11): 14-17.

LIU Kai, LIANG Xiaogeng, LI Younian. Nonlinear target tracking algorithm based on particle filters[J]. Journal of Sichuan Ordnance, 2014(11):14-17. (in Chinese)

5李天成, 范红旗, 孙树栋. 粒子滤波理论、方法及其在多目标跟踪中的应用[J]. 自动化学报, 2015, 41(12): 1981-2002.

LI Tiancheng, FAN Hongqi, SUN Shudong. Particle filtering: theory, approach, and application for multi-target tracking[J]. Acta Automatica Sinica, 2015, 41(12):1981-2002. (in Chinese)

6YIN S, ZHU X. Intelligent particle filter and its application to fault detection of nonlinear system[J]. IEEE Transactions on Industrial Electronics, 2015, 62(6):3852-3861.

7WEI T, HUANG Y, CHEN C L P. Adaptive sensor fault detection and identification using particle filter algorithms[J]. IEEE Transactions on Systems Man & Cybernetics Part C, 2009, 39(2):201-213.

8包瑞新, EDOARDO Sabbioni,于会龙,等. 基于辅助粒子滤波的汽车轮胎参数和行驶状态估计[J/OL]. 农业机械学报, 2015, 46(4):282-288, 301. http:∥www.j-csam.org/ch/reader/view_abstract.aspx?file_no=20150442&flag=1& journal_id=jcsam. DOI:10.6041/j.issn.1000-1298.2015.04.042.

BAO Ruixin, EDOARDO Sabbioni, YU Huilong, et al. Vehicle tire parameter and state estimation under driving situation based on auxiliary particle filter method[J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2015, 46(4):282-288,301. (in Chinese)

9刘洞波,刘国荣,王迎旭,等.基于区间分析无迹粒子滤波的移动机器人SLAM方法[J/OL].农业机械学报, 2012, 43(10):155-160. http:∥www.j-csam.org/ch/reader/view_abstract.aspx?file_no=20121028&flag=1& journal _id = jcsam. DOI:10.6041/j.issn.1000-1298.2012.10.028.

LIU Dongbo, LIU Guorong, WANG Yingxu, et al. SLAM method for mobile robot based on interval analysis unscented particle filter[J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2012, 43(10):155-160. (in Chinese)

10张博, 徐文, 李建龙. 基于粒子滤波的AUV组合导航方法[J]. 机器人, 2012, 34(1):78-83.

ZHANG Bo, XU Wen, LI Jianlong. Particle filter-based AUV integrated navigation methods[J]. Robot, 2012, 34(1):78-83. (in Chinese)

11张毅, 郑潇峰, 罗元,等. 基于高斯分布重采样的Rao-Blackwellized粒子滤波SLAM算法[J]. 控制与决策, 2016, 31(12):2299-2304.

ZHANG Yi, ZHENG Xiaofeng, LUO Yuan. SLAM algorithm with Gaussian distributed resampling Rao-Blackwellized particle filter[J].Control and Decision,2016, 31(12):2299-2304. (in Chinese)

12李永坚. 融合视觉和激光测距的机器人Monte Carlo自定位方法[J/OL]. 农业机械学报, 2012, 43(1):170-174.http:∥www.j-csam.org/ch/reader/view_abstract.aspx?file_no=20120130&flag=1&journal_id=jcsam.DOI:10.6041/j.issn.1000-1298.2012.01.030.

LI Yongjian. Robot Monte Carlo self-localization method based on combination of vision sensors and laser range finder[J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2012,43(1):170-174. (in Chinese)

13YANG X, ADLURU N, LATECKI L J. Particle filter with state permutations for solving image jigsaw puzzles[C]∥Computer Vision and Pattern Recognition, 2011:2873-2880.

14田梦楚, 薄煜明, 陈志敏,等. 萤火虫算法智能优化粒子滤波[J]. 自动化学报, 2016, 42(1):89-97.

TIAN Mengchu, BO Yuming, CHEN Zhimin, et al. Firefly algorithm intelligence optimized particle filter[J]. Acta Automatica Sinica, 2016,42(1):89-97. (in Chinese)

15KWOK N M, FANG G, ZHOU W. Evolutionary particle filter: re-sampling from the genetic algorithm perspective[C]∥IEEE International Conference on Intelligent Robots and Systems, 2016:2935-2940.

16LI T C, SUN S D, SATTAR T P, et al. Fight sample degeneracy and impoverishment in particle fllters: a review of intelligent approaches[J]. Expert Systems with Applications, 2014, 41(8):3944-3954.

17PAK J M, AHN C K, SHMALIY Y S, et al. Improving reliability of particle filter-based localization in wireless sensor networks via hybrid particle/FIR filtering[J]. IEEE Transactions on Industrial Informatics, 2015,11(5):1089-1098.

18GORDON N J, SALMOND D J, SMITH A F M. Novel approach to nonlinear/non-Gaussian Bayesian state estimation[J]. IEEE Proceedings F-Radar and Signal Processing, 2002, 140(2):107-113.

19陈世明, 肖娟, 李海英,等. 基于引力场的粒子滤波算法[J]. 控制与决策, 2017, 32(4):709-714.

CHEN Shiming, XIAO Juan, LI Haiying, et al. The particle filter algorithm based on gravitation field[J]. Control and Decision, 2017, 32(4):709-714.(in Chinese)

20曹洁, 李玉琴, 吴迪. 基于改进差分进化的高精度粒子滤波算法[J]. 上海交通大学学报, 2014, 48(12):1714-1720.

CAO Jie, LI Yuqin, WU Di. A high precision particle filter based on improved differential evolution[J]. Journal of Shanghai Jiaotong University, 2014, 48(12):1714-1720. (in Chinese)

21HAN W, XU J, ZHOU M, et al. Cuckoo search and particle filter-based inversing approach to estimating defects via magnetic flux leakage signals[J]. IEEE Transactions on Magnetics, 2016, 52(4):1-11.

22王法胜, 鲁明羽, 赵清杰,等. 粒子滤波算法[J]. 计算机学报, 2014, 37(8): 1679-1694.

WANG Fasheng, LU Mingyu, ZHAO Qingjie, et al. Particle filtering algorithm[J]. Chinese Journal of Computers, 2014, 37(8):1679-1694. (in Chinese)

23YANG X S, DEB S. Engineering optimisation by Cuckoo search[J]. International Journal of Mathematical Modelling & Numerical Optimisation, 2010, 1(4):330-343.

24GANDOMI A H, YANG X S, ALAVI A H. Cuckoo search algorithm: a metaheuristic approach to solve structural optimization problems[J]. Engineering with Computers, 2013, 29(1): 17-35.

25JOHNZEN C. Cuckoo search: recent advances and applications[J]. Neural Computing & Applications, 2014, 24(1):169-174.

26WANG Y, CAI Z, ZHANG Q. Differential evolution with composite trial vector generation strategies and control parameters[J]. IEEE Transactions on Evolutionary Computation, 2011, 15(1):55-66.

27汪慎文, 丁立新, 张文生,等. 差分进化算法研究进展[J]. 武汉大学学报：理学版, 2014, 60(4):283-292.

WANG Shenwen, DING Lixin, ZHANG Wensheng, et al. Survey of differential evolution[J]. Journal of Wuhan University：Natural Science Edition, 2014, 60(4):283-292. (in Chinese)

28赵志伟, 杨景明, 呼子宇,等. 基于一次指数平滑法的自适应差分进化算法[J]. 控制与决策, 2016, 31(5):790-796.

ZHAO Zhiwei, YANG Jingming, HU Ziyu, et al. Self-adaptive differential evolution algorithm based on exponential smoothing[J]. Control and Decision, 2016, 31(5):790-796. (in Chinese)