基于迭代函数的伪随机序列生成算法

2018-04-18杨涛瑞

数字通信世界 2018年1期

关键词：密码学随机性二进制

杨涛瑞

（重庆育才中学，重庆 400050）

1 引言

伪随机序列是一种具有类似白噪声性质的序列，在信息安全领域和扩频通信领域中都起着非常重要的作用。从某种意义上讲，伪随机序列的安全性确定了整个密码体系的安全性。因此如何得到高质量的伪随机序列成为信息安全热点研究问题[1，2，4]。

如果一个序列是伪随机的，它至少应具有如下性质[1，2，4]：

（1）看起来是随机的，即能通过已知的所有正确的随机性检验。

（2）是不可预测的，也就是说，即使给出产生序列的算法或者硬件设计和以前产生序列的所有知识，也不可能通过计算来预测下一个随机位是什么值。

在本文，一种新的基于混沌迭代映射的伪随机序列生成算法被提出来了。在该方法中，通过对迭代函数输出值和该输出值所在的区间下标进行异或运算，从而得到一个长度为n比特的伪随机序列。

本文其余部分是按如下方式组织的：第2节描述了伪随机序列的生成算法，第3节利用NIST提供的随机性检验方法对生成的伪随机序列进行了随机性检验；最后在第4节对算法进行了总结。

2 伪随机序列的生成

2.1 混沌迭代函数的选择

分段线性混沌迭代函数具有良好随机统计特性，其定义如下：

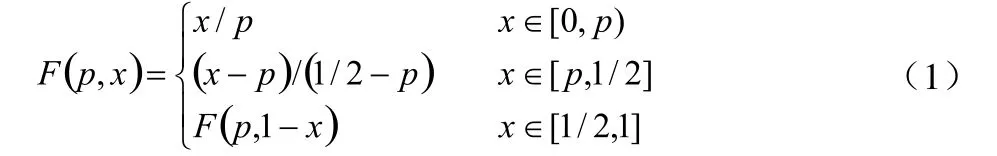
p是控制参数，且p∈（0，1/2）。该混沌映射在区间[0，1]上具有较好的统计特性：输出值满足遍历各态性、混和性和确定性。

2.2 定义新运算“异和”

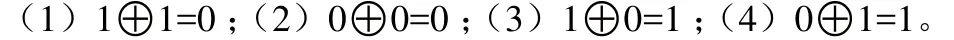
2.3 伪随机序列的生成

本文设计一种伪随机序列生成算法，其原理框图如图1所示。

步骤1：将区间[0，1]划分为等距的256个子区间，记为Δi，i=0，1 255。每个区间的取值范围是 [i·2-8，（i+1）·2-8]。

步骤2：根据给定的初始值x0，控制参数p和初始迭代次数N0，迭代映射F（x0，p），得到输出xi。

步骤3：比较xi与步骤1的各个子区间，记下xi落入子区间 Δi的下标 i。

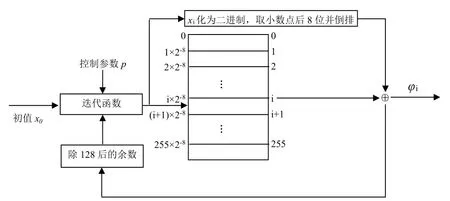
图1 伪随机序列生成框图

步骤4：将十进制数xi转化为二进制形式，取其小数点后8位并将其倒排；将步骤3得到的i也表示为8位的二进制形式。然后将这两个二进制形式的8位进行按位异或运算，得到一个8位的输出比特流，记为φi。

步骤5：将φi除以128得到的余数赋给N0（如果余数为0，则将128赋给N0），作为计算下一个8位输出比特流时函数的迭代次数。

重复步骤2～步骤5若干次，一个期望的伪随机序列（φ1，φ2， φn）就得到了。

3 伪随机序列的随机性测试

建立在假设检验基础上的随机性测试是一种重要的测试方法，假设检验是一类重要的统计推断问题，它依据小概率原理，即如果一个事件在现有假设下发生的概率很小，那么一旦这一事件发生，则认为该假设成立，则我们接受这种假设。

美国国家技术与标准局（NIST）推出的STS（Statistical Test Suite）是当前伪随机性测试中最具权威的工具，其中给出了16种随机序列测试的方法，其显著性水平a∈[0.001，0.01]。当每组随机性检测的概率值（p-value）大于a，即p-value> a则接收该假设，反之则拒绝。根据NIST的建议，当通过率大于等于98.056%时则认为通过了该项随机性检验。

实验过程中，我们生成了1000组长度为1，000，000比特的位序列。用STS工具软件检测，实验结果如下（表1）。表中的实验数据每一测试项的通过率均大于98.056%，表明算法产生的伪随机序列通过了所有的随机性测试，即可以认为算法所产生的伪随机序列有较好的随机性。

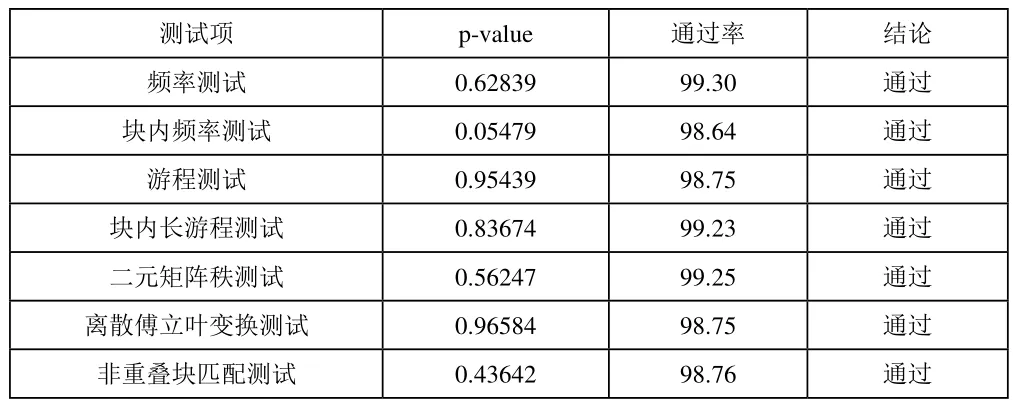
表1 随机性测试

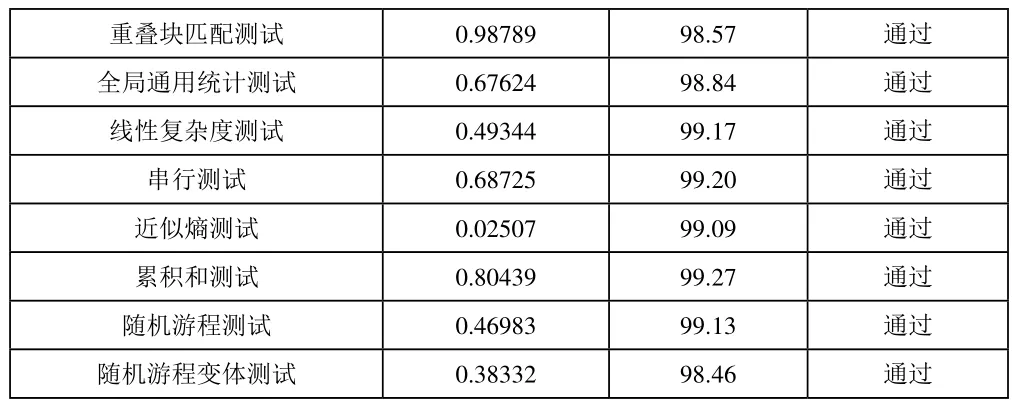
重叠块匹配测试 0.98789 98.57 通过全局通用统计测试 0.67624 98.84 通过线性复杂度测试 0.49344 99.17 通过串行测试 0.68725 99.20 通过近似熵测试 0.02507 99.09 通过累积和测试 0.80439 99.27 通过随机游程测试 0.46983 99.13 通过随机游程变体测试 0.38332 98.46 通过