多元线性回归的整车质心高度预测方法

刘海江，周 雷，邓志刚

（同济大学 机械与能源工程学院，上海 201804）

整车质量开发是整车性能开发中的一个重要环节，整车质心位置作为整车质量开发中的关键参数之一，是整车质量开发工作中的重中之重[1]。当整车质量目标制定后，需要对整车质心位置（质心高度）进行预测，以验证车辆的操纵稳定性、安全性等性能是否满足需求。但在项目开发初期，由于绝大多数零部件的设计还未锁定，也没有实际样车下线，所以难以得到车辆质心高度的实测值。此时就需要对车辆的质心高度进行预测，以供其他部门开发用。当前开发中对质心高度的预测基本以经验公式为主，或以工程师自身的经验为主，该方法的明显缺点是预估的质心高度精度较低，某些情况下无法满足开发的需要。因此，整车质心高度的预测在整车质量开发中不容忽视，其精度的提高有利于缩短整个项目开发的周期，并提升整车性能开发的可靠性。

国内外学者及科研机构对车辆质心位置的估算、测量及其对性能的影响进行了广泛的研究。重庆长安汽车股份有限公司的孙阳坤等[2]针对车辆在开发过程中的不同阶段提出了不同的整车质心预估方法。爱尔兰的SOLMAZ等[3]提出了一种基于多模型、多转换的车辆质心位置实时测量的新方法，并使用计算机模拟验证了该新方法的可行性。美国密西根大学基于复摆原理，开发了一种车辆惯性参数测量装置，利用该装置可测得车辆的质心高度[4]。日本的MIKATA等[5]提出一种利用地秤测量质心位置的方法，该方法能有效测量带集装箱的运输车的质心位置。哈尔滨工业大学的赵新通等[6]利用静态称重法测量车辆质心位置，同时设计了一种2自由度运动平台，并对其误差进行了分析和计算。西南交通大学的丁军君等[7]通过建立重车车辆模型，研究了重心高度对动力学性能的影响，车辆重心高度对横向平稳性以及安全性影响较大。大连理工大学的徐平平[8]利用有限元法对不同质心位置的皮卡车分别以不同速度碰撞刚性墙进行了仿真分析，数据显示整车变形量随着质心位置的改变而发生相应的变化，同时质心位置对汽车的判速方程也会产生影响。目前，关于车辆质心位置的研究主要集中在车辆质心位置测量方法的改进、新测量装置的开发以及质心高度对车辆性能的影响，对项目开发初期车辆质心位置的预测研究相对较少。在项目初期，车辆的很多零部件及总成未完全确定，因此很难预测出较为精确的车辆质心位置。

本文通过对与整车质心高度有关的影响因素进行分析，确定整车质心高度预测的关键因素，找出质心高度影响因素与质心高度间的映射关系，并通过多元线性的回归分析法建立了整车质心高度预测模型，进而为项目开发初期车辆质心高度的预测提供有力的支撑。

1　整车质心位置计算方法及质心高度预估指标选择

1.1　整车质心位置计算

整车质心位置在水平x轴和y轴方向的变化一般较小，z轴方向偏移过大将直接影响车辆的安全性能，因此质心高度是车辆质心位置的关键。车辆质心位置计算公式如下。

水平质心位置计算（质心至后桥中心距离）

式中：m后为空载时后轮轴荷，kg；l为底盘轴距，mm；m为整备质量，kg。

质心高度位置计算

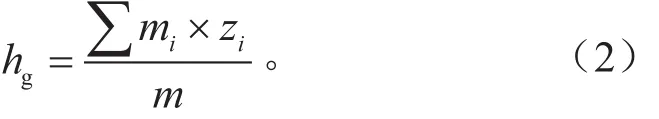
式中：mi为车辆各总成质量，kg；zi为各总成质心高度，mm。

由前述整车质心位置计算公式可知，得到车辆的前后轴荷、轴距和整备质量即可计算出质心的水平位置，由此也就能够比较准确地预测，质心的水平位置一般比较容易得到。由式（2）可知，车辆质心高度的计算涉及到众多零部件及总成的质量及其对应的质心高度，相对于质心水平位置的计算，质心高度的计算要复杂得多，因此质心高度就成为确定整车质心位置的关键。

1.2　整车质心高度预估指标选择

研发初期，由于很多设计细节还未确定，且没有实际样车下线，也就很难得到实测的整车质心高度。在这个阶段需要对整车质心高度进行预测，以便为底盘、安全等模块的选型、仿真及验证提供可靠的输入。

由于普通级轿车在乘用车销售量中占据主导地位，本文拟选取普通级轿车（通常所说的A级车）的质心高度为研究对象，即可以不考虑前述车型不同对整车质心高度的影响。此外，由于普通级轿车普遍采用发动机前置前轮驱动的布置方式，因此整车布置形式的影响也可以不予考虑。

由整车质心高度的计算公式可知，车辆的整备质量会对整车质心高度产生重要影响。发动机是汽车中最主要的总成之一，乘用车的发动机质量占整备质量的比例一般在12%～20%之间，因此其质量的变化对整车质心位置将产生较大的影响。汽车的变速器是汽车传动系统中最重要的总成之一，变速器自身的质量在整备质量中的比例一般是3%～9%之间，同时同级别车手动和自动变速器之间的质量相差很大，其对质心位置的影响不可忽略。车轮和轮胎是汽车行驶系统中的主要零部件，车轮和轮胎质量对整车质心高度的影响主要在其本身，然而不同规格的轮胎尺寸也会使车的整体高度发生改变，进而影响整车质心高度。整车质心高度是指车辆在满油状态时的质心高度，因此燃油箱的容积对质心高度会产生影响。后备厢的容积不同也会对质心高度产生影响。汽车天窗位于汽车顶部，不同配置的天窗其质量存在差异，进而对质心高度产生影响。

综上所述，在对普通级轿车的质心高度进行预测时，关键指标主要是整车尺寸参数、整备质量和关键总成质量，关键总成主要包括发动机、变速器、车轮和轮胎、天窗、燃油箱和后备厢等。

2　基于多元线性回归分析质心高度预测模型建立

通过以上分析，在确定影响整车质心高度预测的关键因素的过程中，发现质心高度受多个因素影响，此时需要用两个以上的影响因素作为自变量来解释因变量的变化。多元线性回归分析可以准确地计量各个因素之间的相关程度与回归拟合程度的高低，相较于其它方法，多元线性回归更加简单方便并易于理解，同时也可提高预测方程式的效果，因此，建立整车质心高度与其影响因素的多元线性回归模型，并采用最小二乘法实现其回归模型。

2.1　多元线性回归模型

整车质心高度预测的多元线性回归模型可表示为：

对整车质心高度进行预测的过程中会得到多组不同的数据，在获得n组观测数据后，可将式（3）表示为：

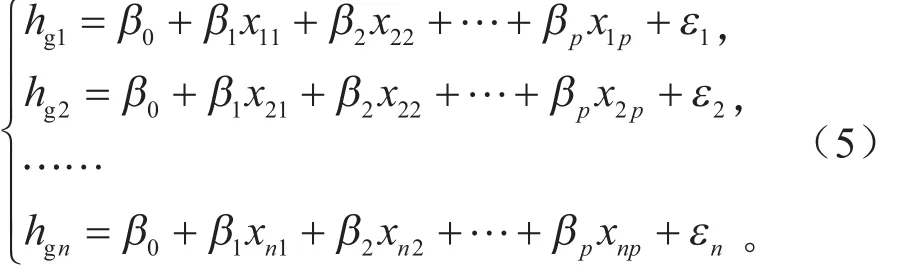
式（5）可用矩阵形式表示为：

其中

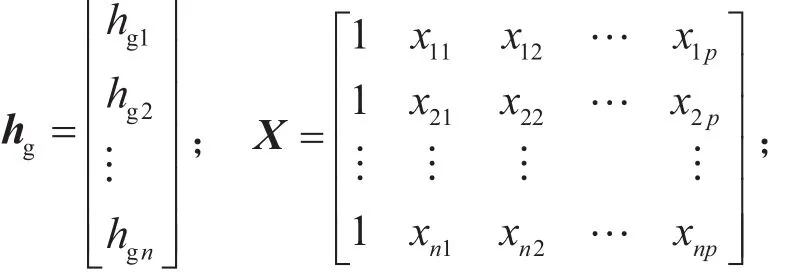
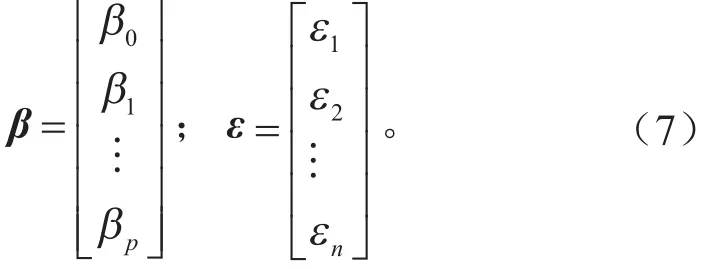
式中：hg为整车质心高度矩阵，hg1,hg2, …,hgn为各所选择的指标的质心高度；X为整车质心高度预估指标矩阵，X11,X12, …,X1p,…,Xnp为各所选指标的特征值；为整车质心高度预估指标对应的特征系数矩阵为对应指标的特征系数；为随机误差矩阵为对应指标的随机误差。

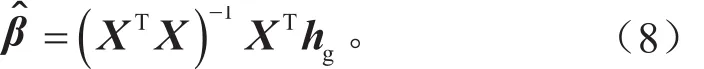
2.2　多元线性回归模型的检验

多元回归方程的检验主要通过样本决定系数R2表示其拟合程度，因此，本文所提出的整车质心高度预测模型的拟合程度可以用决定系数R2（0≤R2≤1）来判定。R2越接近1，表明整车质心高度预测模型回归拟合的效果越好。

式中：RSS为残差平方和；TSS为总离差平方和；为自变量对因变量的预测值；为平均值。

3　试验验证及结果分析

为了验证所建立的质心高度预测模型的拟合效果，随机选择了30台普通级轿车，测量获得了相应的数据，从中选择恰当的30个参数，见表1。

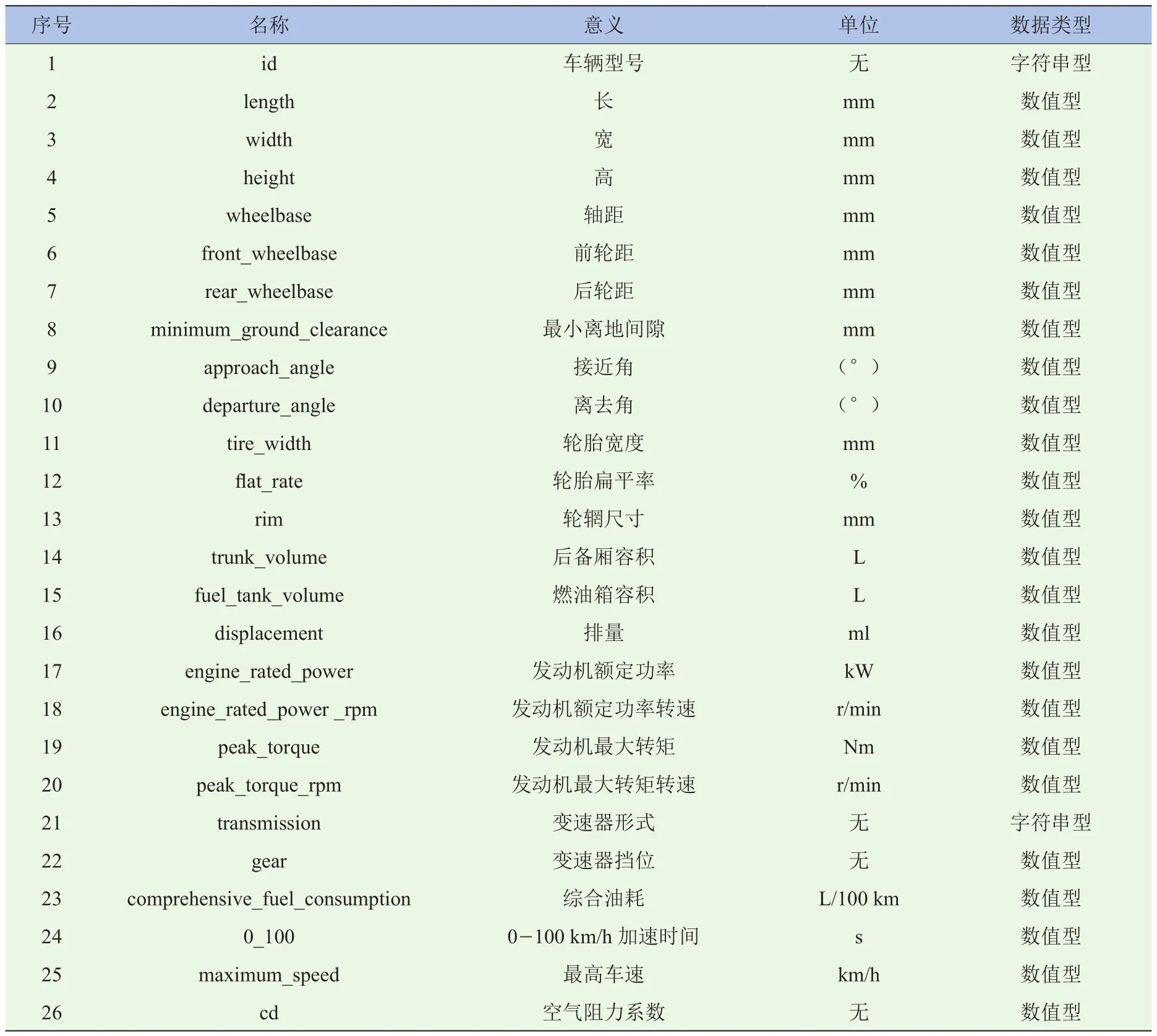
表1　汽车指标参数

续表1

然后使用Weka回归分析系统获得对本预测模型贡献度大的整车质心高度预估指标，然后通过所测得的样车数据应用最小二乘法计算求得对应指标的特征系数 ，最终得到质心高度预测回归方程：

回归方程相关指标见表2。

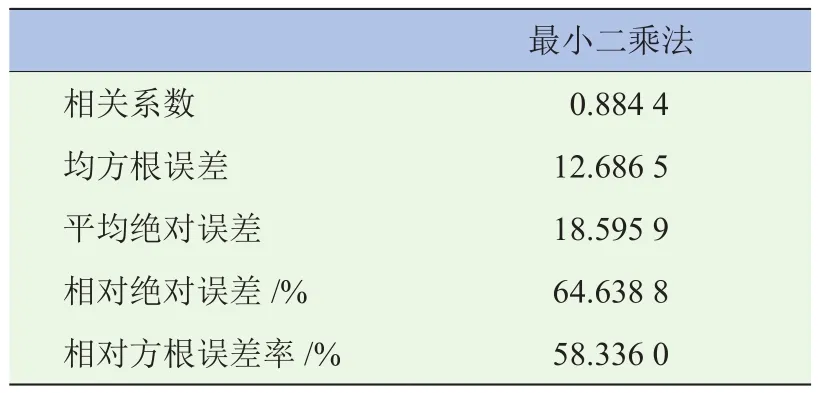
表2　质心高度回归分析结果

其相关系数为0.8844，表明质心高度与其影响因素具有较高的线性相关性，质心高度预测模型的拟合效果好。

为了进一步验证质心高度预测模型的准确性，通过将质心高度预测模型的值、工程师通过大量经验获得的传统方法求得的值与质心测量设备VIMF测量的值进行对比验证。

本研究所采用的质心测量设备为美国SEA公司开发的整车惯性测量设备，如图1所示。

图1　VIMF总体布置

采用VIMF系统的整车质心高度测量方法，从中随机抽取10台普通级轿车，对其质心高度进行测量，各总成的质量信息见表3。针对这10台车，利用回归分析法和传统经验法对整车质心高度进行预测，并对误差进行分析，分别计算预测值与测量值，求得绝对误差与相对误差，其结果见表4。

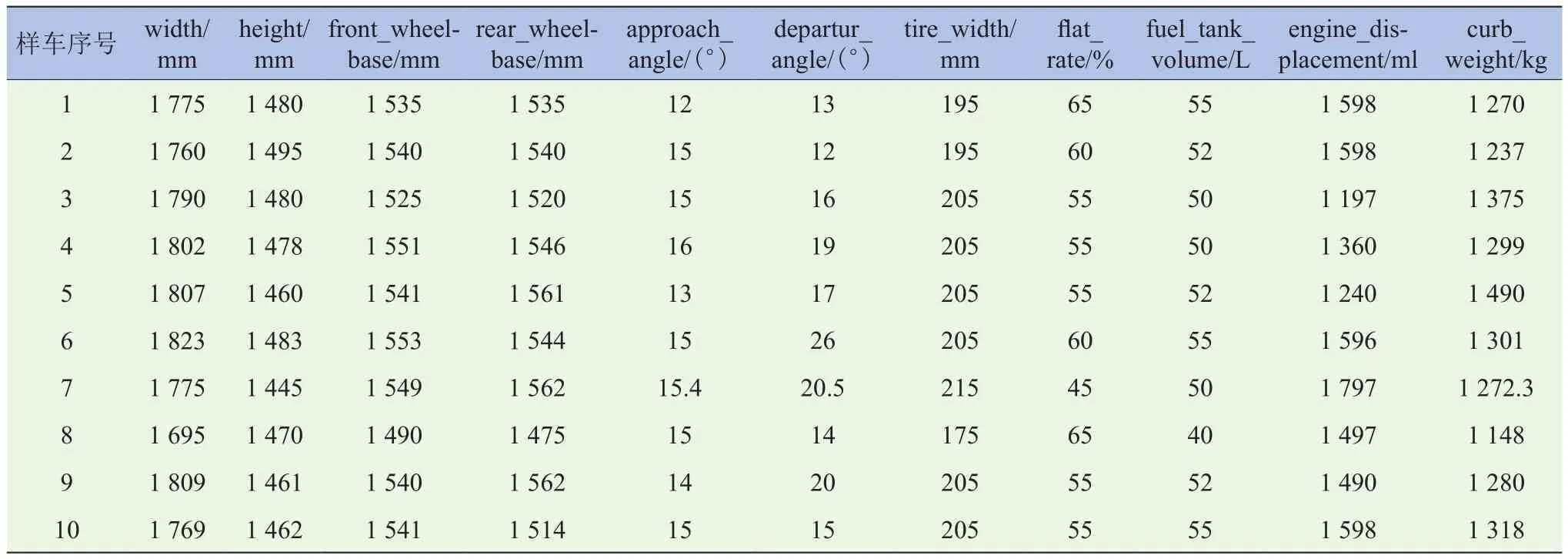
表3　整车质心高度指标各总成的质量信息

表4　整车质心高度实际测量及预测结果

将表4中回归分析法和传统方法所计算得到的绝对误差值用折线图作分析对比表示，如图2所示。

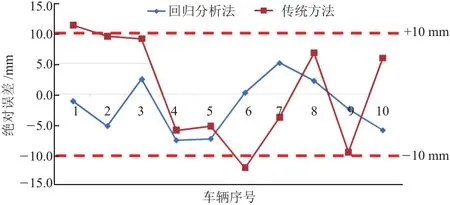
图2　回归分析法与传统方法绝对误差对比

在实际工程开发中，一般对整车质心高度预估的绝对误差要求为±10 mm，在此误差范围内的整车质心高度一般能有效降低底盘选型、仿真及调校、安全性仿真等的风险。由图2可知，运用回归分析法对整车质心高度进行预估时，其绝对误差均在±10 mm的范围内，而运用传统方法对整车质心高度进行预估时，有2台车的预测值已超过±10 mm的裕度范围。

运用回归分析预测模型和传统整车质心高度预测方法，针对所选车型参数，可以得到整车质心高度预测结果。用统计学对结果进行分析，可以得到回归分析法和传统方法的平均误差，见表5。

由表5可知，回归分析预测的平均误差比传统方法预测的平均误差小。结合表4以及图2的分析结果可知，回归分析法在整车质心高度的预测中其精度优于以经验公式计算的传统预测方法。此外，由于传统方法是基于整车高度对整车质心高度进行预测，一般同一款车型下的所有配置都采用相同的尺寸参数，即同一款车型下不同配置的整车高度往往是一样的，此时，若仍采用传统方法对整车质心高度进行预测，将会造成所有配置的整车质心高度预测值完全一样。但实际情况是，由于配置的不同，车辆的动力总成、内饰、外饰等往往会存在一定差异，因此也会导致同一车型下不同配置车辆的整车质心高度不一样。采用回归分析法预测整车质心高度时，考虑了对整车质心高度影响较大的多个因素，因此能有效避免传统方法预测时的弊端。

表5　预测结果平均误差统计

4　结论

本文以普通级轿车为例，参照乘用车质心高度影响因素，确定整车质心高度的影响因素为整车尺寸参数、整备质量和关键总成质量。根据质心高度影响因素与质心高度的关系，通过回归分析法建立了整车质心高度预测的多元线性回归模型。利用Weka数据挖掘软件，基于现有车辆的质心高度数据，对建立的多元线性回归模型进行求解，得到了整车质心高度预测的函数关系，解决了传统方法无法预测同一款车型下不同配置车辆的质心高度问题，同时也解决了一定精度要求下整车质心高度的有效预测问题，为整车质量开发提供了科学依据，从而在项目前期就能够最大程度地降低项目风险，缩短开发周期、降低开发成本，提高整车性能开发的可靠性。

参考文献（References）：

[1]WEBER J. Automotive Development Processes [M].Berlin Heidelberg：Springer，2014.

[2]孙阳坤，王靖，罗国政，等. 汽车质量及质心估算研究[C]//2015中国汽车工程学会年会论文集(Volume 4)，中国汽车工程学会，2015.SUN Yangkun，WANG Jing，LUO Guozheng，et al.Automobile Quality and Centroid Estimation [C]//2015 China Automotive Engineering Society Annual Conference(Volume 4)，China Automotive Engineering Society，2015. (in Chinese)

[3]SOLMAZ S，AKAR M，SHORTEN R. Online Center of Gravity Estimation in Automotive Vehicles Using Multiple Models and Switching[C]//9th International Conference on Control，Automation，Robotics and Vision，December 5-8，Singapore. Piscataway，N.J：IEEE Press，c2006：342-348.

[4]DURISEK N J，GRANAT K J，HEYDINGER G J，et al. Repeatability and Bias Study on the Vehicle Inertia Measurement Facility(VIMF)[C]//SAE World Congress& Exhibition，Detroit，Michigan，2006.

[5]MIKATA Y，YAMANAKA M，KAMEOKA K，et al.Measuring the Center of Gravity with Truck Scale[C]//Proceedings of the SICE Annual Conference，September 13-18，2011，Tokyo，Japan. Piscataway，N.J：IEEE Press，c2011：1254-1257.

[6]赵新通，姜洪洲，韩俊伟. 车辆质心位置测量系统的研制[J]. 哈尔滨商业大学学报(自然科学版)，2004，20(3)：304-306，312.ZHAO Xintong，JIANG Hongzhou，HAN Junwei.Development of Vehicle Center of Mass Position Measuring System [J]. Journal of Harbin University of Commerce(Natural Science Edition)，2004，20(3)：304-306，312. (in Chinese)

[7]丁军君，李芾，黄运华. 车辆重心高度对动力学性能的影响[J]. 铁道机车车辆，2008，28(6)：32-36.DING Junjun，LI Fei，HUANG Yunhua. Effects of Vehicle Height of Gravity on Dynamic Performance [J]. Railway Rolling Stock，2008，28(6)：32-36. (in Chinese)

[8]徐平平. 不同质心位置皮卡车正面碰撞事故分析[D].大连：大连理工大学，2008.XU Pingping. Accident Analysis of Head-on Crash of Pickup Truck with Different Center of Mass [D]. Dalian：Dalian University of Technology，2008. (in Chinese)