基于变量代换的高中数学解题研究

唐瑜

四川省仁寿第一中学校北校区 四川眉山 620010

数学知识具有抽象性导致其难度较大，对于大多数高中生来说，数学解题主要难点在于如何正确选择解题思路，不同的解题思路对应不同的解题步骤，同时计算也存在较大差异。如果解题思路出现了偏差，很可能导致解题失败[1]。变量代换是高中数学解题中较为常见的一种解题方法，适用于一些常见类型的数学题目，掌握这一方法能够有效提高数学解题效率。

1 变量代换在三角函数解题中的应用

三角函数是高中数学知识体系中最为复杂的内容之一，在实际生活中有一定的应用。三角函数问题多出现在计算题和应用题中，所占分值也较高[2]。因此，高中生应重点关注三角函数的解题技巧，并明确应用变量代换的题目类型。

解析：利用常规方法解题，需要进行多次三角函数转化，在这个过程中，极易出现转化失误，同时计算量也较大。而应用变量代换，可以使整个解题过程更加清晰、明了。

之中可得：

对①进行三角函数转化后可得：

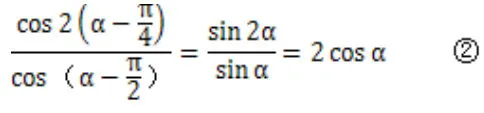
2 函数解题中变量代换的应用解析

在高中数学解题中，函数知识的应用较为普遍。然而，与几何、向量等题目对比，函数题目具有抽象性导致其解题较为困难，在实际解题过程中，除了使用数形转换降低其难度以外，对于无法明确数形关系的题目，则可尝试使用变量代换的方式进行解题[3]。

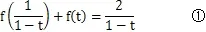
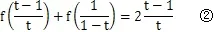
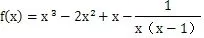
3 变量整体代换在高中数学解题中的应用

在变量代换法的应用过程中，存在一些较为特殊的题型，也就是所谓的整体变量代换。整体变量代换的应用具有一定的限制条件，应慎用这一方法，否则，将破坏原题的数学关系。

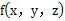
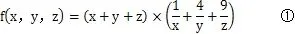
展开后得：

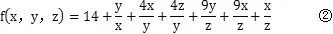
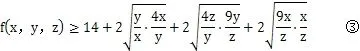
4 结语

变量代换丰富了数学解题方法，扩展了解题思路，这对于提高数学解题效率有着极为重要的作用。变量代换在实际解题中具有一定的适用性，所以，我们应当通过大量的练习掌握这一解题方法，提高自身逻辑思维能力，同时培养个人的数学综合素养。