高中物理与物体受力分析方法研究

宋思程

郑州龙湖一中 河南郑州 450000

力学是高中物理众多知识点中较为复杂的部分，其涉及内容较为广泛，且生活化应用较强，属于高考物理中的必考内容。在高中物理力学题目中，分析物体的受力最为关键，力学受力分析直接影响到解题效率与正确率。因此，在学习力学相关基础知识的同时，我们还需要通过大量的练习熟悉不同类型的力学受力分析技巧。

1 物体受力分析概述

力的矢量特征具有大小、方向两个要素。因此，在对物体进行受力分析时，我们需要综合考虑物体的实际受力情况，结合题目需要分解受力[1]。高中物理中的物体受力分析方法主要包括整体法、正交分解法等多种类型，我们需要根据题目的具体情况选择对应的受力分析方法，以提高解题效率。

2 基于整体法的物体受力分析

整体法是物体受力分析中较为常见的一种方法，其优点在于它能够忽略系统中的内力作用，尤其是对于一些无法明确的内力作用，其可以通过整体进行受力分析[2]。

例1：在水平面上放置一三角形斜面B，斜面上有一小木块A，三角形斜面B的质量为M，小木块A的质量为m，如图1所示。与水平面相平行的力F朝相反方向推动A和B，若A和B都未移动，则以下两种表述是否正确：

2.1 A、B之间的摩擦力无法确定

2.2 水平面受到的B的压力为（M+m）g

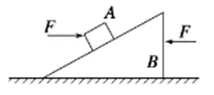
图1

解析：将A和B看作一个整体，其水平受力只有两个大小相等、方向相反的力F。因此，在水平方向上可以看作没有外力作用，由A、B组成的系统对水平面的压力也就是（M+m）g，则可得出（2）的结论。

在（1）中，在不考虑B受力的情况下，如果直接施加A的力F在沿斜面向上的力分解后与mg沿斜面向下的分解力的大小相等，则A与斜面B之间不存在摩擦力。因此，A与B之间的摩擦力无法确定。

3 正交分解法在物体受力分析中的应用

正交分解法多见于直角关系的物体受力分析中，通常情况下，涉及重力的物体受力分析题目适用于正交分解法。但是，正交分解法的使用不具有唯一性，需要结合物体受力的实际情况进行判断。

例2：如图所示，在水平放置的斜面上有一小木块A，已知斜面的倾角为，如果斜面相对于小木块的动摩擦因素为，若在保持斜面固定的情况下，对小木块施加水平方向上的力F，试问当F为多少时，小木块能够在斜面上匀速向上运动？

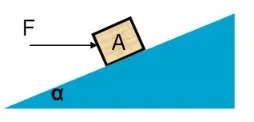
图2

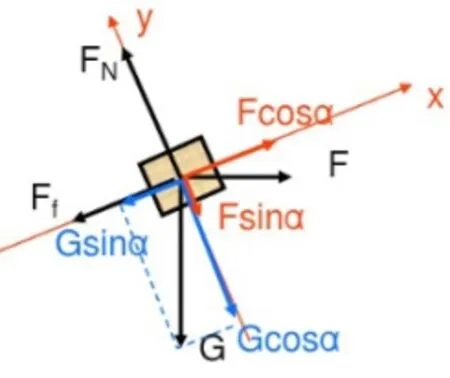
图3

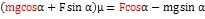
4 结语

除了以上两种类型的物体受力分析方法，在一些题目中，由于其无法使用正交分解法，所以其可以利用力的矢量特性，通过矢量三角形法对物体进行受力分析。物体受力分析的方法多种多样，我们要在巩固力学知识的基础上，通过大量的练习掌握物体受力分析的具体方法，以提高解答力学题目的效率。