高维核矩阵极化码的蒙特卡洛设计方法＊

黄志亮，张施怡，周水红

(浙江师范大学数理与信息工程学院，浙江 金华 321004)

0　引言

由Arikan提出的极化码，被证明了在连续消去（SC）译码算法下，其可以达到二进制输入对称离散无记忆信道（B-DMCs）的对称容量，并且有着多项式级数的编译码复杂度[1]。尽管极化码的构造是明确的，但只有在二进制删除信道（BEC）下的构造是有效的[1]。Mori和Tanaka表明在一般信道下，密度进化（DE）[2]方法是一种有效构造极化码的工具[3]。基于密度进化方法，研究者主要[3-4]提出两类方法用于原2×2维核矩阵极化码的构造：高斯近似DE（GA-DE）方法[3]和Tal-Vardy方法[4]。GA-DE方法有着线性的复杂度，并且其构造的极化码有着优异的性能。Tal-Vardy方法是一种量化的DE方法[4]。Tal-Vardy方法提供两种信道升级和降级的近似量化方法，原始的位信道夹在这两种方法构造的位信道之间。由于这两种方法是构造出的极化码是极其接近的[4]，因此Tal-Vardy方法被认为是最优的极化码构造方法。

构造高维核矩阵极化码最直接的方法就是将GA-DE和Tal-Vardy方法从G2推广到高维核矩阵。然而，在推广这两种方法时存在一些问题。①GA-DE方法：Huang等人[7]提出了一种-表达式方法用来获得任意高维核矩阵在似然比域中SC译码算法的简化递归公式。基于-表达式，可以利用GA-DE方法构造相应高维核矩阵极化码[7]。然而，对于高维核矩阵极化码，由于-表达式中引入了相关，其违背了高斯假设（多个独立同分布的随机变量相加的分布近似位高斯分布），因此GA-DE方法产生一定的失真。②Tal-Vardy方法：由于单步递归位信道输出集合的元素个数，随着核矩阵的维数m指数地增长，所以直接将Tal-Vardy方法推广至高维核矩阵极化码是不实际的。

另一种用来构造极化码方法是Arikan在其原始文章中提出的基于蒙特卡洛（MC）的极化码构造方法[1]。然而，后续仅仅少数的研究者[8]利用这种方法来构造极化码。文献[8]关于MC构造方法设计极化码是针对G2核矩阵的。本文深入分析了基于MC的极化码构造方法，将其进一步推广至了高维核矩阵极化码的设计中，表明了MC构造方法对于高维核矩阵极化码也是一种快速而有效的方法。

本文主要有三个方面的贡献。首先，分析了MC构造方法，从理论上表明了其有效性；第二，对于高维核矩阵极化码，在连续消去（SC）译码和列表SC（LSC）下，MC构造方法比GA-DE方法有着更优的性能；第三，与原G2核矩阵相比，高维核矩阵极化码获得相当大的性能提升。

本文安排如下。第二节给出文章中所使用的符号和定义，描述了极化码构造的本质。第三节描述了本文的研究动机。第四节首先描述了如何利用MC构造方法来设计高维核矩阵极化码，然后给出MC构造方法的性能和复杂度分析。第五节给出仿真结果。第六节总结了文章。

1　准备工作

1.1　符号

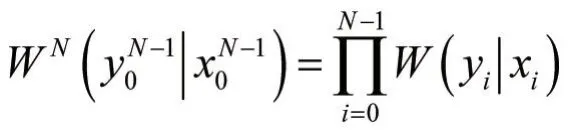
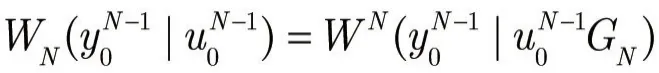
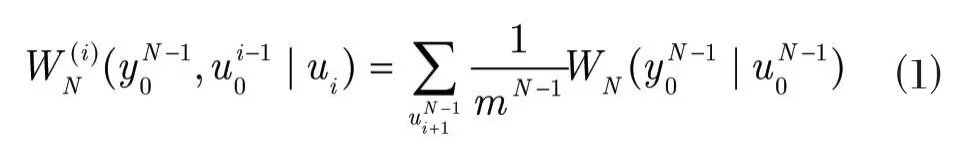
对于一个给定的核矩阵Gm，定义为：

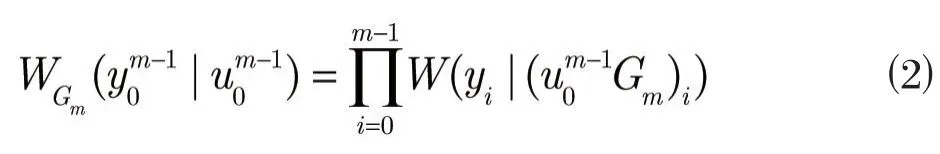
对于SC译码，基本的递归计算公式（单步位信道计算公式）为：

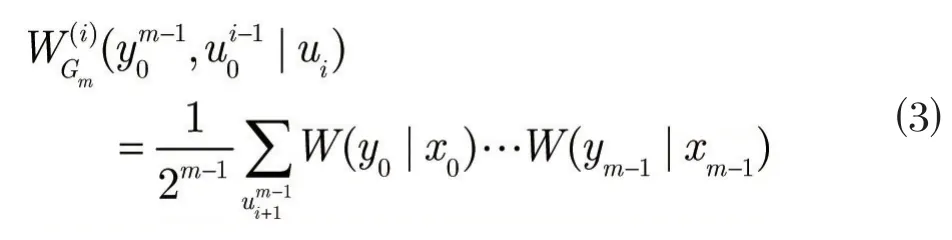
1.2　极化码构造

实质上，构造一个k维的极化码就是找到k个最可靠的位信道。Arikan[1]使用巴氏参数来评价位信道，从所有N个位信道中挑选k个有着最小的位信道作为信息位集合。Tal和Vardy[4]使用更易操作的对位信道进行排序，表示在最大似然判决下第i个位信道的差错概率。本文采用来评价位信道。

1.3　基于W-表达式的SC译码

Korada等人[5]指出一个高维的Gm核矩阵极化码的直接SC译码复杂度为。Huang等人[7]提出一个W-表达式方法简化递归公式fk0和的计算。当m≤16时，基于W-表达式，SC译码复杂度降低为。因此，本文采用基于W-表达式的SC译码。

2　研究动机

由于GA-DE和Tal-Vardy方法推广至高维核矩阵的困难，本研究采用MC构造方法来设计高维核矩阵极化码。下面将详细介绍推广GA-DE和Tal-Vardy方法构造高维核矩阵极化码的难点。

2.1　GA-DE方法

下面用一个简单的例子阐述GA-DE方法构造的高维核矩阵极化码会有一定程度失真。

例1（一个G6核矩阵的-表达式）[7]：

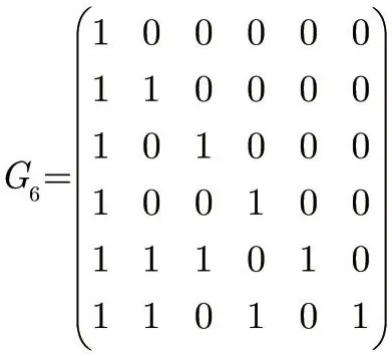
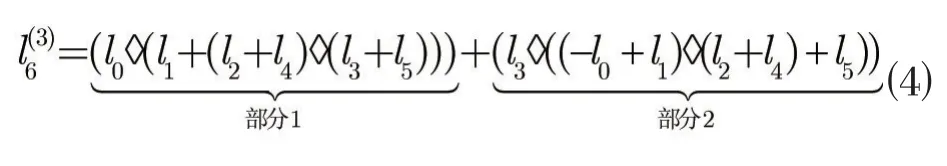
2.2　Tal-Vardy方法

不失一般性，考虑G2核矩阵的递归信道转化如下：

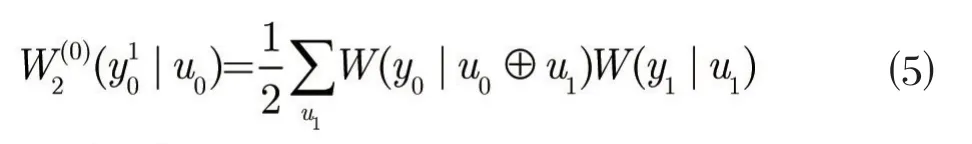
然而对于高维核矩阵，Tal-Vardy方法是不实际的。Tal-Vardy方法可以分解为两步：①构造信道；②输出字母集大小从μ2减少到μ。给定一个Gm核矩阵，递归公式⑸变为：

3　蒙特卡洛构造方法

MC构造方法模拟SC译码过程：首先，对每一位重复执行SC译码；其次，通过大量的仿真，并基于每一位的差错概率来评估每个位信道；最后，对所有位信道的差错概率排序，选择具有最低差错概率的K个位信道作为信息位集合。

3.1　蒙特卡洛构造方法

重复执行SC译码，MC构造方法用每一位的差错概率评估每个位信道，并选择具有最低差错概率的最佳K个位信道作为信息位。令M表示SC译码的重复执行次数。算法2描述了MC构造方法。在算法2中，第8步采用基于W-表达式的SC译码算法进行译码，对于给定的信息位ui，如果其译码结果为1，则；否则不变。在MC构造方法中（和是成正比的）用来评价位信道。

3.2　蒙特卡洛构造方法的分析

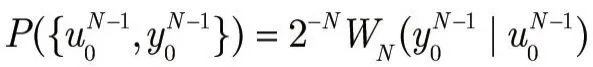
令：

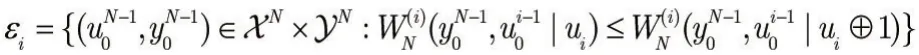
有：

令：

实际上，[1，Corollary 1]证明了等式⑻。

因此，根据⑺，⑻，⑼，有：

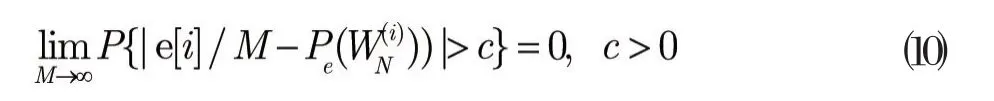
3.3　M的值

根据⑽式，通过使用更大的样本的M，MC构造方法可以任意准确地估计。然而，一个更大的M意味着更高的复杂度。由于的值趋向于0或1，所以MC构造方法受益于极化现象，并不需要太大。实验结果表明最优的M不需要太大。

4　仿真

考虑二进制相移键控（BPSK）调制和一个加性高斯白噪声（AWGN）信道。特别的，二进制码字x=(x0,…,xN-1)基于sn=1-2xn映射到一个传输序列s=(s0,…，sN-1)。在接收端，获得接收向量y=(y0,…,yN-1)，其中yn=sn+zn，z=(z0,…，zN-1)是独立同分布随机变量，它们都满足均值为0和方差为N0/2的高斯分布。

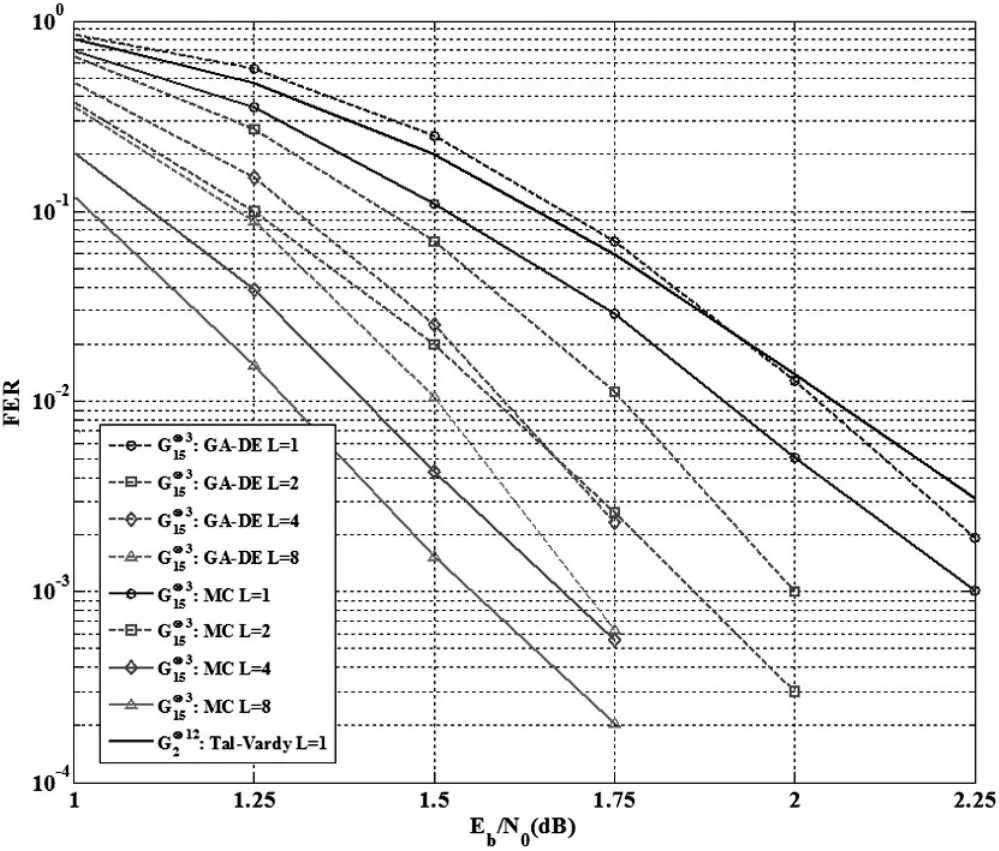
图2　MC构造方法和Tal-Vardy方法构造的极化码在LSC译码下的FER

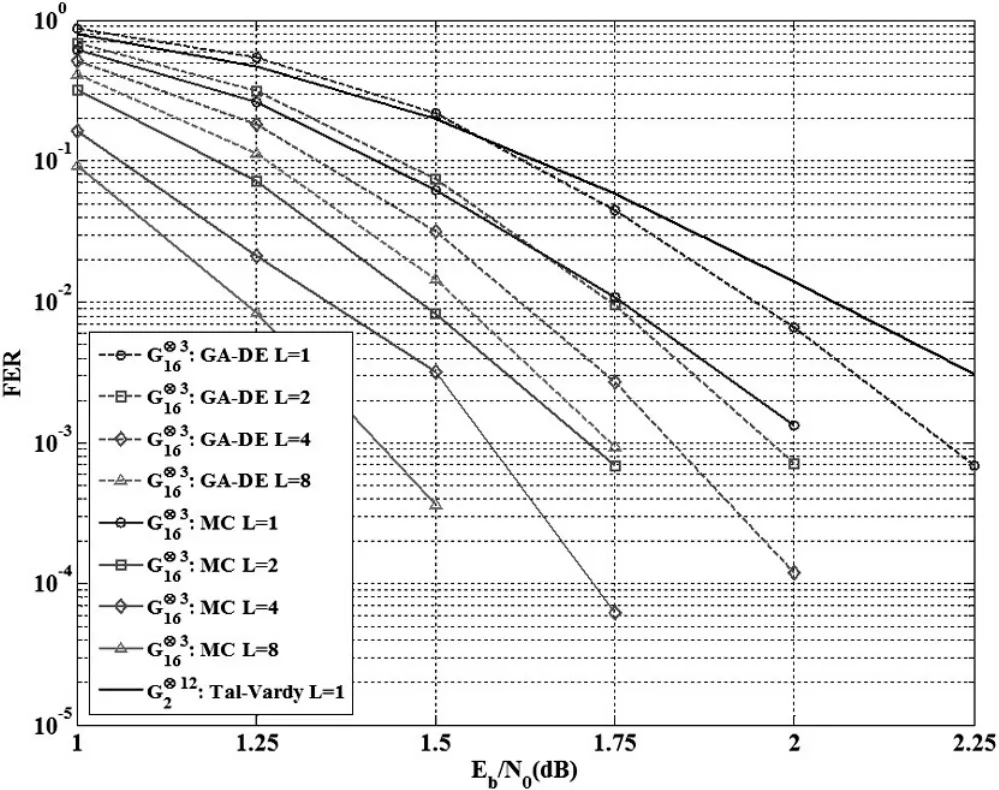
图3　MC构造方法和Tal-Vardy方法构造的极化码在LSC译码下的FER

图2表明在SC和LSC译码下，用MC方法构造的极化码明显优于GA-DE方法构造的极化码，也表明在SC译码（L=1）下，相比于极化码，用MC构造方法构造的极化码获得相当大的性能提升。所有的码在SNR=2.0dB构造。图3表明在SC和LSC译码下，相比于Tal-Vardy方法构造的极化码，MC方法构造的极化码有着明显的性能提升。

仿真结果证明了以下两点：①对于高维核矩阵，用MC构造的极化码明显优于GA-DE方法构造的极化码;②相比于G2核矩阵极化码，高维核矩阵极化码获得明显的性能提升。

5　结论

为了有效地构造高维核矩阵的极化码，提出一个基于蒙特卡洛方法的极化码构造方。本文从理论上分析了蒙特卡洛方法计算的位信道差错概率是实际差错概率的准确估计。仿真结果表明：①对高维核矩阵极化码，MC构造方法明显优于GA-DE方法；②相比于G2核矩阵极化码，MC构造方法构造的高维核矩阵极化码获得明显的性能提升。因此，本文研究表明MC构造方法是一个有效的高维核矩阵极化码构造方法。

参考文献(References):

[1]Arikan E.Channel Polarization:A Method for Constructing Capacity-Achieving Codes for Symmetric Binary-Input MemorylessChannels[J].IEEETransactions on Information Theory,2009.55(7):3051-3073

[2]Mori R and Tanaka T.Performance of polar codes with the construction using density evolution[J].IEEE Communications Letters,2009.13(7):519-521

[3]Trifonov P.Efficient Design and Decoding of Polar Codes[J].IEEETransactions onCommunications,2012.60(11):3221-3227

[4]Tal I and Vardy A.How to Construct Polar Codes[J].IEEE Transactions onInformation Theory,2013.59(10):6562-6582

[5]Korada S B, Şaşoglu E,and Urbanke R.Polar Codes:Characterization ofExponent,Bounds,and Constructions[J].IEEETransactions onInformation Theory,2010.56(12):6253-6264

[6]Lin H P,Lin S,Abdel-Ghaffar K A S.Linear and NonlinearBinaryKernelsofPolarCodesofSmall DimensionsWithMaximumExponents[J].IEEE Transactions on Information Theory,2015.61(10):5253-5270

[7]Huang Z,Zhang S,Zhang F,Duan C,and Chen M.On the Successive Cancellation Decoding of Polar Codes with ArbitraryLinearBinaryKernels[J].CornellUniversity Library,http://arxiv.org/abs/1701.03264,accessed Dec.3.2017.

[8]Wu D,Li Y,and Sun Y.Construction and Block Error Rate Analysis of Polar Codes Over AWGN Channel Based onGaussianApproximation[J].IEEECommunications Letters,2014.18(7):1099-1102