Five-equation and robust three-equation methods for solution verification of large eddy simulation *

Rabijit Dutta, Tao Xing



Five-equation and robust three-equation methods for solution verification of large eddy simulation*

Rabijit Dutta, Tao Xing

Large eddy simulation (LES), OpenFOAM, periodic channel flow, solution verification

Introduction

With the advent of the high-performance com- puting facilities, high-fidelity computational fluid dynamics (CFD) simulations using large eddy simulation (LES) are being regularly used in academic research and industrial applications. However, due to the lack of proper guidelines for verification and validation (V&V), often these simulations are either under-resolved or over-resolved. Since LES employs simpler algebraic models compared with Reynolds- averaged Navier-Stokes (RANS) based turbulence models, an under-resolved LES could be more erroneous than a RANS solution. An over-resolved LES with negligible sub-grid stress, also called quasi direct numerical simulation (DNS), provides a solu- tion identical to a DNS solution if the same numerical algorithms are used. However, the computational cost of an LES is much greater than a DNS at the same grid due to the involvement of extra modeling terms/ equations. Therefore, quantification of numerical and modeling errors on different grid resolutions for LES is essential for significantly improving the reliability, risk assessment, and decision making of LES in scientific and engineering applications.

Various V&V methods have been established for CFD. These include grid convergence index (GCI) method and its variants[1-3], least square method[4], correction factor method[5, 6]and the factor of safety method[7, 8]. However, these V&V methods were developed for RANS based turbulence models, where the sources of errors and uncertainties can be categorized into modeling and numerical errors, and each of them can be separately evaluated. For impli- citly filtered LES, local grid spacing acts as a cut-off filter, and sub-grid scale model uses the local grid spacing as the turbulent length scale parameter to model the effects of unfiltered scales on the resolved scales of motion. Therefore, the numerical and modeling errors change simultaneously when the grid size varies. As a result, they are difficult to estimate.

In the current study, the various V&V methods proposed by Xing[16]were evaluated using many datasets from LES of periodic channel flows on eight systematically refined grids and time-step sizes. Dutta and Xing[17]presented preliminary data on periodic channel flow using seven grids and showed that the numerical and modeling errors have opposite signs in six and seven-equation methods. In the next section, the methodology of LES is discussed. Then, the V&V methodology and their implementation in the current framework are briefly described followed by results, discussions, and conclusions.

1. Methodology of LES

1.1 Governing equations

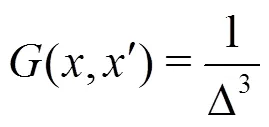
1.2 Filtered Navier-Stokes equations

Applying a filter to the incompressible Navier- Stokes equations results in the following sets of equa- tions[18]

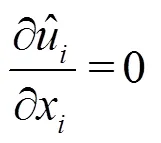
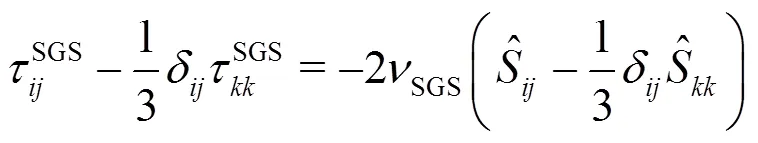
1.3 Geometry, numerical scheme and parameters

Fig. 1 (Color online) Computational geometry and vortical structures

2. Solution verification procedure

2.1 LES error methods

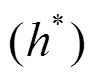
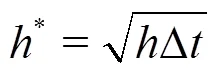
Table1 Details of the grid sizes and time step sizes used in the computations; the grid spacing in, and direc- tions are presented in wall units (, and), denotes the bulk velocity in the channel

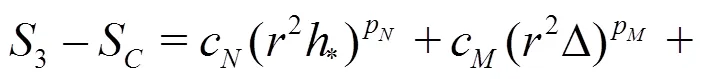
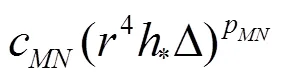
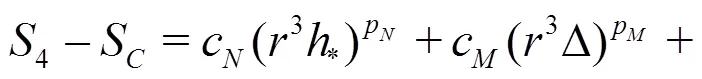
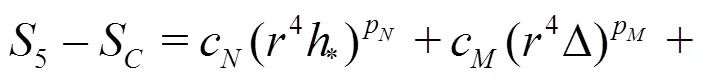
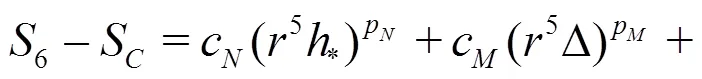
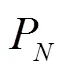
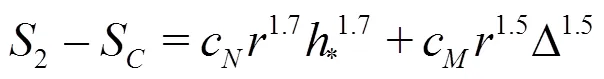
Equations(20)-(22)can be solved analytically by the method of substitution:

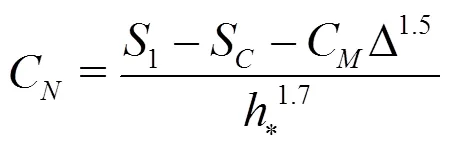
2.2 Solution of nonlinear equations

(1)Residual of any equation is higher than the magnitude of either numerical error or modeling error in that equation.

(2)Zero magnitudes of either numerical or mode- ling error.

Finally, the solution with the minimum condition number was selected.

2.3 RANS error methods

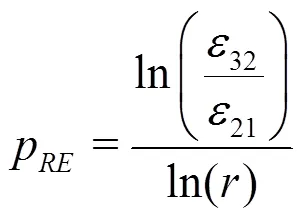
2.4 LES index of quality index based on turbulent kinetic energy

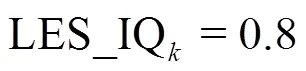
3. Results and discussion

3.1 Mean flow and turbulence quantities

Fig. 2Effect of grid refinement on mean velocities and turbu- lent fluctuations (normalized using the friction velocity)

Fig. 3 Effect of grid refinement on resolved turbulent kinetic energy and Reynolds shear stresses (normalized using square of the friction velocity)

3.2 Relation between error and LES index of quality

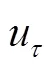
3.3 Performance of various LES V&V methods

(1)The stiffness of solving equations for me- thods

(2)Convergence characteristics of numerical, modeling, and coupling errors

Table2Evaluation of LES error estimates

3.4 Comparison of LES and RANS methods

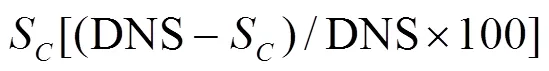
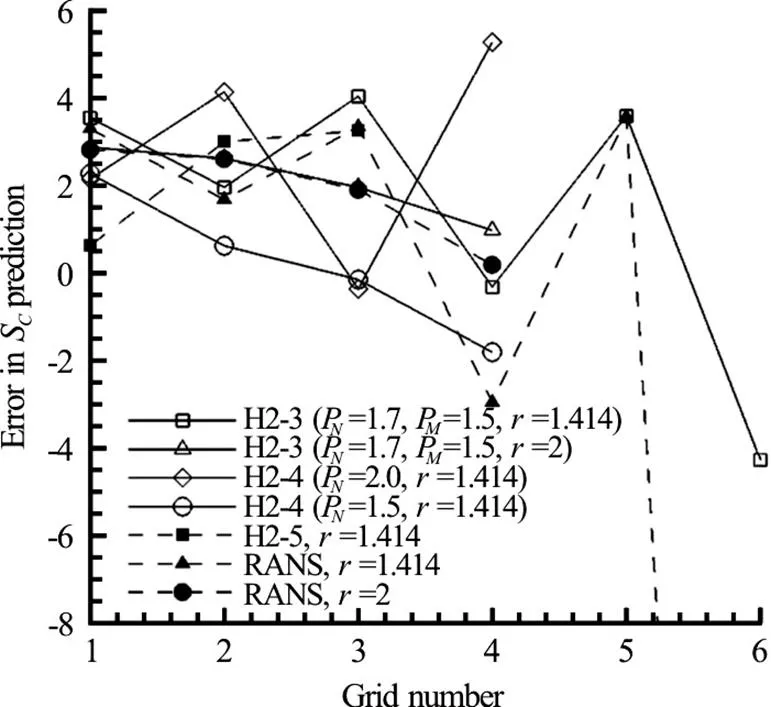
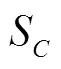
3.5 Convergence of numerical, modeling and total errors for LES V&V methods

3.6Further evaluation of the proposed three-equation method H2-3

Fig. 6Numerical, modeling, and total errors for different LES V&V methods

(1) The three-equation method is robust as it can be applied to any convergence type of LES whereas the RANS method based on Richardson Extrapolation can only be applied for monotonic convergence.

(2)For each convergence type, the three-equation method reasonably predicts the increase of the error magnitudes when the coarse grid solution is moving fartherawayfromtheother twogridsolutionsforMC and when the fine grid solution is moving farther away from the medium grid solution for OC, OD, and MD.

Table 3Evaluation of three-equation method using contrived grid convergence studies

(3)Numerical and modeling errors predicted by the three-equation method have similar magnitudes and show opposite signs for all convergence types. All of them shows negative numerical errors and positive mo- deling errors except for MDs that show the opposite.

4. Conclusions and future directions

(1)From the most sophisticated method H1-7 based on Hypothesis I, i.e., the one without assuming any values for the seven unknowns, the coupling error is at least one order of magnitude smaller than the nume- rical/modeling errors, which suggests that Hypothesis II is more feasible to apply as it requires much lower com- putational costs. The seven-equation method and the simplified six and five equations based on Hypothesis I include non-linear equations that are difficult to solve. Therefore, all the methods based on Hypothesis I are not recommended.

(4)Contrived grid convergence study suggests that H2-3 method is robust and can be used for monotonic convergence, monotonic divergence, oscillatory conver- gence and oscillatory divergence on a grid triplet.

(5) Almost all the LES V&V methods show that the numerical and modeling errors have opposite signs, which suggests error cancellation play a key role in LES.

(6) To apply existing RANS method to evaluate SCin LES could lead to large errors on coarse meshes. However, if the grid is fine enough to resolve more than 80% of the total turbulent kinetic energy, RANS method likely predicts reasonable numerical benchmark as well.

Acknowledgement

The authors would like offer gratitude to Idaho National Laboratory (INL) for providing HPC resou- rces for running all the simulations.

[1] Roache P. J. Verification and validation in computational science and engineering [M]. Albuquerque, New Mexico, USA: Hermosa Publishers, 1998.

[2] Roache P. J. Fundamentals of verification and validation[M]. Albuquerque, New Mexico, USA: Hermosa Publishers, 2009.

[3] Oberkampf W. L., Roy C. J. Verification and validation in scientific computing [M]. Cambridge, UK: Cambridge University Press, 2010.

[4] Eça L., Hoekstra M. A procedure for the estimation of the numerical uncertainty of CFD calculations based on grid refinement studies [J]., 2014, 262:104-130.

[5] Stern F., Wilson R. V., Coleman H. W. et al. Comprehen- sive approach to verification and validation of CFD simulations-Part 1: Methodology and procedures [J]., 2001, 123(4): 793-802.

[6] Stern F., Wilson R., Shao J. Quantitative V&V of CFD simulations and certification of CFD codes [J]., 2006, 50(11): 1335-1355.

[7] Xing T., Stern F. Factors of safety for Richardson extrapo- lation [J]., 2010, 132(6): 061403.

[8] Xing T., Stern F. Closure to "Discussion of 'Factors of Safety for Richardson Extrapolation'" (2011, ASME J. FluidsEng.,133,p.115501)., 2011, 133(11): 115502.

[9] Meyers J., Sagaut P. Is plane-channel flow a friendly case for the testing of large-eddy simulation subgrid-scale models? [J]., 2007, 19(4): 048105.

[10] Geurts B. J., Frӧhlich J. A framework for predicting accu- racy limitations in large-eddy simulation [J]., 2002, 14(6): L41-L42.

[11]Celik I. B., Cehreli Z. N., Yavuz I. Index of resolution quality for large eddy simulations [J]., 2005, 127(5): 949-958.

[12]Celik I., Klein M., Janicka J. Assessment measures for engineering LES applications [J]., 2009, 131(3): 031102.

[13] Gousseau P., Blocken B., Van Heijst G. J. F. Quality as- sessment of Large-Eddy Simulation of wind flow around a high-rise building: Validation and solution verification [J]., 2013, 79(Suppl. C): 120-133.

[14]Klein M. An attempt to assess the quality of large eddy simulations in the context of implicit filtering [J]., 2005, 75(1): 131-147.

[15]Freitag M., Klein M. An improved method to assess the quality of large eddy simulations in the context of implicit filtering [J]., 2006, 7: N40.

[16]Xing T. A general framework for verification and valida- tion of large eddy simulations [J]., 2015, 27(2): 163-175.

[17]Dutta R., Xing T. Quantitative solution verification of large eddy simulation of channel flow [C]., Las Vegas, USA, 2017.

[18] Pope S. B.Turbulent flows [M].Cambridge, UK: Cambridge University Press, 2000.

[19] Yoshizawa A., Horiuti K. A statistically-derived subgrid- scale kinetic energy model for the large-eddy simulation of turbulent flows [J]., 1985, 54(8): 2834-2839.

[20] Dejoan A., Schiestel R. LES of unsteady turbulence via a one-equation subgrid-scale transport model [J]., 2002, 23(4): 398-412.

[21]Smagorinsky J. General circulation experiments with the primitive equations: I. The basic experiment [J]., 1963, 91(3): 99-164.

[22]Germano M., Piomelli U., Moin P. et al. A dynamic subgrid-scale eddy viscosity model [J]., 1991, 3(7):1760-1765.

[23]Nicoud F., Ducros F. Subgrid-scale stress modelling based on the square of the velocity gradient tensor, flow [J]., 1999, 62(3): 183-200.

[24]Kim J., Moin P., Moser R. Turbulence statistics in fully developed channel flow at low Reynolds number [J]., 1987, 177: 133-166.

[25] De Villiers E. The potential of large eddy simulation for the modelling of wall bounded flows [D]. Doctoral Thesis, London, UK: University of London, 2007.

[26]Gullbrand J. Grid-independent large-eddy simulation in turbulent channel flow using three-dimensional explicit filtering [C]., San Francisco, USA, 2003.

(November 14, 2017, Accepted December 23, 2017)

©China Ship Scientific Research Center 2018

Rabijit Dutta (1984-), Male, Ph. D.

Tao Xing,

E-mail: xing@uidaho.edu