基于聚类分析方法的CCD测量原井下煤仓 煤位改进测量模型研究

黎　宾

(广西电力职业技术学院，广西 南宁 530007)

0　引　言

井下煤仓煤位测量是井下自动作业控制的重要检测参数，能实时提供煤仓的储料情况，是煤矿井下作业自动化以及安全生产设计的重要环节。由于工作环境恶劣，井下煤仓煤位测量一直是国内外煤炭工业测量装置研究的难点，常用的测量方法有电容式煤位探测、重锤式煤位探测、核辐射式煤位探测和超声波式煤位探测系统等。运用图像处理技术实现井下煤仓煤位测量技术源自于光学三维轮廓技术[1]。目前,CCD物料料位测量的主要工作原理有通过辅助点光源成像后的位移变化计算物料高度[2]和通过辅助光源成像后的光斑面积变化计算物料高度[3]两种，但这两种原理最核心的计算处理均为辅助光源成像后的光斑轮廓处理以及图像数据的标定，尤其前者所采用的基本算法是一致的。辅助光源在井下煤仓内产生光斑恶劣的情形大多为光斑灰度值较小情形，也就是煤尘的干扰较大情形，文献[4]和文献[5]图像处理结果表明恶劣情形下获取比较准确的光斑直径比较困难，其光斑面积明显要比实际光斑面积小。从文献[4]和文献[5]的图像预处理数据来看，在光斑灰度值较大的情况下，检测光斑的中心坐标相对容易，并且相对准确。本文采用的CCD测量方法也是一种基于辅助光源成像光斑中心点辨识的测量方法，能正确处理光斑灰度值较小的恶劣干扰情形，并且具冗余及校正能力，适用于井下煤仓煤位测量。

1　测量原理

根据摄像机的成像原理，两个共面交叉安装的点光源在被测物面上形成特征光点，当物料高度变化时，特征光点的两种变化值均与物料高度变化值相关：特征光点的像素位移值；特征光点间的成像点间距。式(1)表明了物料高度与特征光点的间距的线性映射关系，即物料高度与特征光点的间距成正比，比例系数仅与点光源的投射角度α、θ相关。

h=h1-(d-h0tgθ)/(tgθ-tgα)

(1)

考虑到摄像机焦距的影响，根据成像基本原理，物料高度与焦距成反比，根据图1得出式(2)。

(2)

将式(2)代入式(1)即可得到物料高度测量模型，见式(3)。

(3)

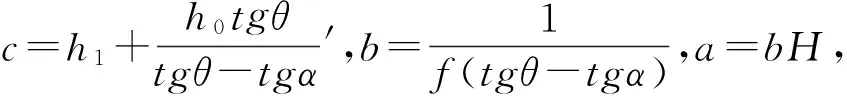
(4)

图1　测量校正原理图

由于煤仓粉尘干扰比较大，并且煤块的堆积状况是随机的，恶劣情形下可能导致点光源不能形成成像光斑或者成像光斑失真，因此，用双测量原理校正方式不失为一个好的选择，特征光点像素的位移值计算具有独立测量原理但又与上述测量方式共享测量器件，必然成为本文的首选校正测量方式。两点效验原理是一致的，取其中一点做分析。

假定点光源和CCD中心线共面且交于一点，且CCD垂直于物面安装。假定物面1为设定的参考零点，物面2为待测高度物面，则物面高度h与其他参数的关系为式(5)和式(6)。

(5)

(6)

令c=L-h0tgθ，b=f(c/H+tgθ)，a=H，则简写为式(7)。

(7)

式(7)与文献[1]中模型的区别在于h所关联的参数是相对于参考面成像点的相对位移，而非相对于CCD中心线相对位移。CCD中心线相对位移与摄像头安装的三维位置均密切相关，如果在测量过程中摄像头中心线发生变化，则会出现较大测量误差，需要重新校正CCD摄像头中心线。而与式(7)相对应的参考面成像点相对位移只与CCD摄像头安装高度相关，不受CCD中心线位置影响。相对于中心线而言，CCD摄像头安装高度易于校正，CCD摄像头安装更为简易。

2　光斑成像特点分析及提取算法

影响测量精度的主要因素在于光斑质心坐标确定，图2是典型的粉尘干扰下的成像光斑图，也是光斑质心坐标确定误差最大的干扰情形。目前，已知的图像处理算法很难适用于所有的图像处理场合，针对特定的图像特征设计针对性的图像处理算法，不失为一种可行的工程设计选择。图2所示的粉尘干扰以及煤炭表明漫反射干扰的光斑图显示，煤炭表面由于漫反射形成若干随机噪声，这些随机噪声具有距离光斑中心距离相对较远以及面积较小等特征。光斑中心由于粉尘干扰光斑的灰度梯度从边缘到光斑中心均具有较大值，并且其梯度变化与粉尘的局部浓度相关，具有一定的随机性。

图像平滑的高斯函数表达式见式(8)。

G(x，y)=e-(x2+y2)/(2σ2)/(2πσ2)

(8)

高斯函数的二阶方向导数见式(9)。

(9)

原始图像f(x，y)变换后的输出图像F(x，y)的卷积分表达式见式(10)。

(10)

图3为Gauss-Laplachian算子图像分割效果，可以看出Gauss-Laplachian算子能基本分割出粉尘干扰下的光斑成像图，但受煤碳表面的漫反射以及灰尘干扰的影响较大。

图2　粉尘干扰下的光斑成像图

图3　Gauss-Laplachian算子图像分割效果

图2可知光斑的边缘是灰度值梯度较大的地方，但灰度值梯度较大的地方不一定是边缘。光斑图呈现出两个特点：边缘的灰度梯度较大，并且各向同性，因此采用Gauss-Laplachian算子图像分割具有一定的效果；边沿的灰度值相近，即便在粉尘干扰较大的情形下，光斑中心的灰度值明显要大于光斑边缘的灰度值，也就是在粉尘干扰下光斑成像后的灰度值从边缘到中心有递增的趋势，这是因为光斑能量呈高斯分布。因此，本文应用图像固有特征利用聚类分析方法设计Gauss-Laplachian算子的阈值，对图像轮廓提取算法进行分割。

将pi记为灰度为i的像素点概率，ni为灰度为i的像素点个数，则在整个灰度级为N的图像中，pi的计算式见式(11)。

(11)

根据光斑的亮度将图像中的像素按阈值分为光斑像素集合C0和背景集合C1，假定以灰度值j为阈值界限，则其方差分别为式(12)和式(13)。

(12)

(13)

其中

(14)

其内间方差和内内方差分别记为σB、σW,见式(15)和式(16)。

(15)

(16)

图3应用Gauss-Laplachian算子图像分割算法所提取的光斑质心和图4应用改进算法所提取的光斑质心相比较，图4所提取的质心与真实光斑中心更为接近。图3的光斑质心由于粉尘干扰以及散射的缘故，轮廓线向光散射方向偏移，从而使得光斑质心朝着成像模糊的区域偏移。光斑质心偏移后直接影响到测量误差，其误差比见表1和表2。

图4　采用聚类分析改进后的Gauss-Laplachian 算子图像分割效果

3　测量模型标定以及模型参数的在线辨识

测量的准确性一方面与光斑的检测与提取相关，另一方面与模型的标定相关。式(4)和式(7)需要点光源与CCD镜头共面的假设条件，而实际安装过程中很难满足这一假设条件。因此式(4)中的参数a、参数b、参数H以及式(7)中的参数a、参数b需要修正以及标定。分别将式(4)和式(7)改写成最小二乘参数辨识模型，见式(17)和式(18)。

h=[-d′d′h1][abc]T

(17)

(18)

模型均归化为标准的最小二乘格式，见(19)，采用标准的最小二乘原理即可进行参数辨识。

y(h)=x(h)θT+e(h)

(19)

光斑的中心坐标可采用重心法求取。设Iij为像素(i，j)的灰度值，Lx和Ly分别为单位像素的X轴、Y轴上的长度分量，R为提取的光斑区域，则光斑的质心坐标表达式为式(20)。

(20)

重心法计算质心能有效利用光斑的高斯能量分布特点，能比较有效处理粉尘干扰后的灰度值噪声，

示值比较稳定。

4　测量数据及结论

系统采用的CCD像素为576 dpi×768 dpi，镜头焦距为5 m，测量高度0～6 000 mm，图像灰度化采用逆滤波算法进行预处理，分别采用Gauss-Laplachian算子阈值分割和用聚类分析算法改进后进行Gauss-Laplachian算子阈值分割，光斑中心采用质心坐标计算，模拟现场环境采取随机粉尘干扰，其测量结果见表1和表2。

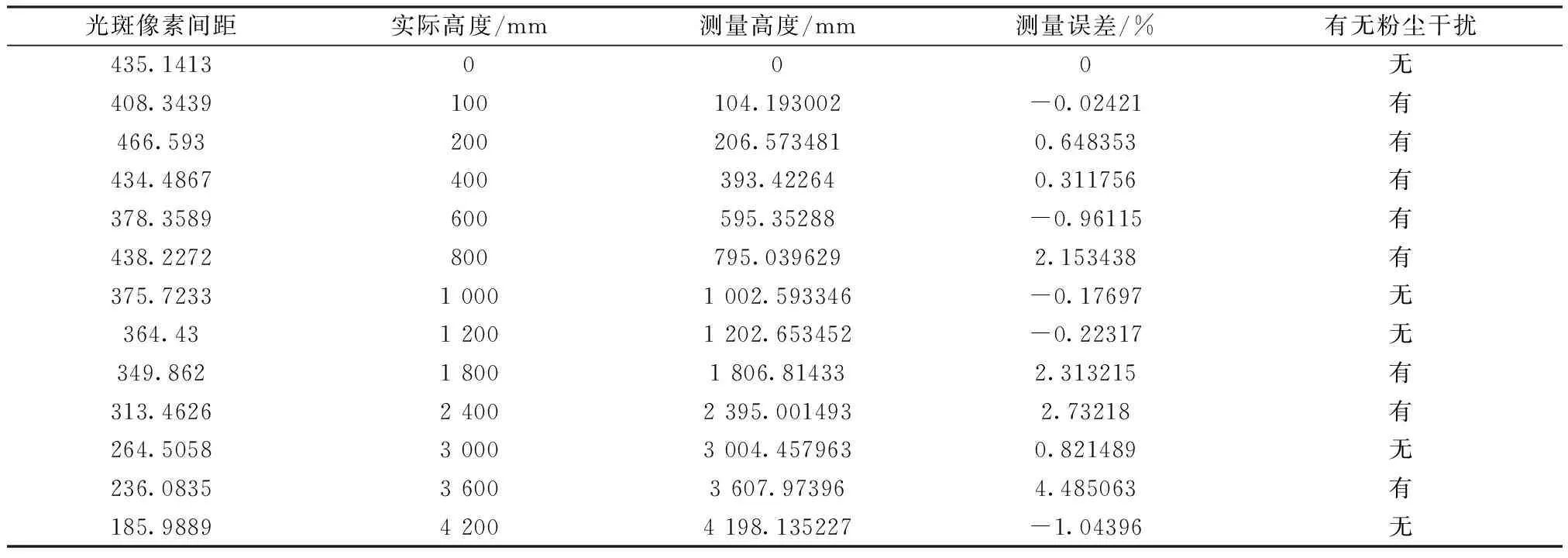
表1　Gauss-Laplachian算子阈值分割算法测量数据(随机粉尘干扰)

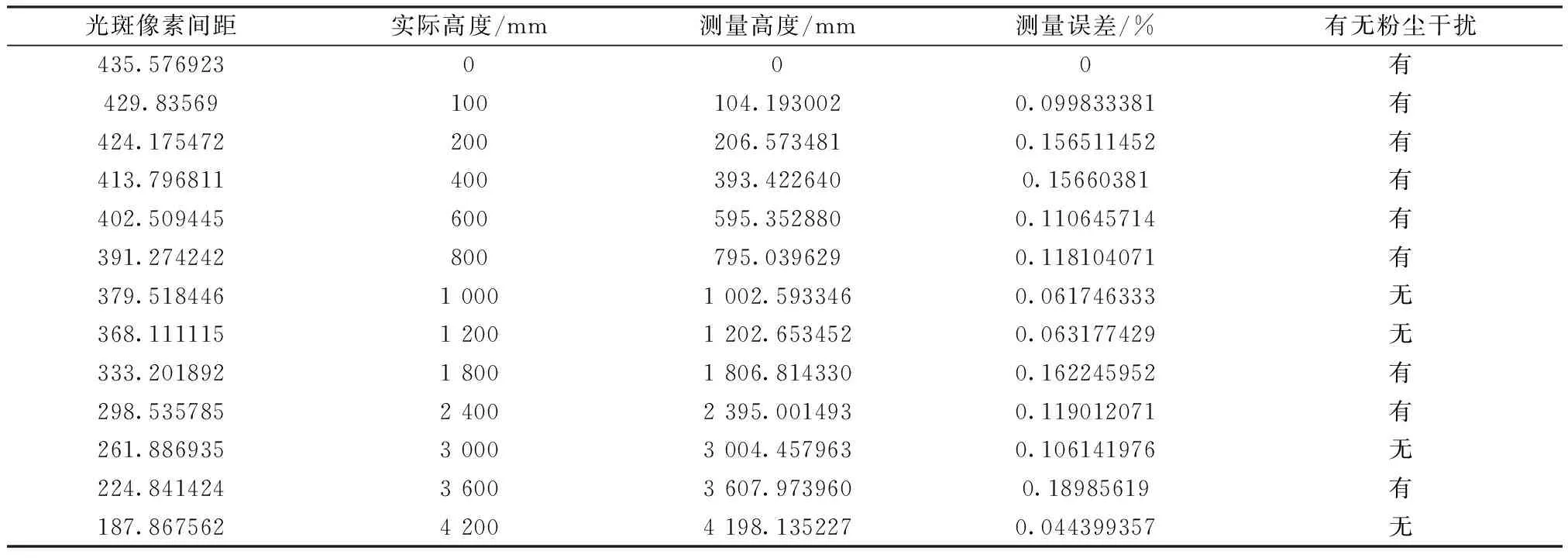
表2　改进算法测量数据(随机粉尘干扰)

从表1和表2的两组数据来看，采用Gauss-Laplachian算子阈值分割算法在粉尘干扰情况下质心的计算偏差较大，但测量精度高于0.05，可用于工程应用，采用聚类分析算法改进后的Gauss-Laplachian算子阈值分割算法，粉尘干扰同样对测量数据有较大影响，但测量精度高于0.002。测量数据的准确度一方面需要模型的精确性，这一点通过测量模型的参数辨识已基本解决，另一方面需要光斑质心的确定，这需要非常准确地提取光斑的质心坐标。双辅助光源的设计、冗余测量原理的校正有助于提高测量数据的可靠性和稳定性。

[1]LUCA Biancardi，GIOVANNA Sansoni，FRANCO Docchio.Adaptive Whole-Field Optical Profilometry：A Study of the Systematic Errors[J].IEEE Transaction On Instrumentation and Measurement，1995，44(1)：36-41.

[2]宋华，孟晓风.一种基于CCD的物位测量方法[J].仪器仪表学报，2002，23(2)：115-118.

[3]潘国林，高幼年.基于机器视觉煤仓料位测量方法的研究[J].上海电力学院学报，2007，32(2)：176-178.

[4]孙继平，吴冰，刘晓阳，等，基于膨胀/腐蚀运算的神经网络图像预处理方法及其应用研究[J].计算机学报，2005，28(6)：985-990.

[5]董玉杰，贾西科，吴冰.井下煤仓煤位不规则光斑图像的检侧方法研究[J].中国煤炭，2013，39(4)：68-70.