无人微耕机的自动转向控制器设计

王佳琪， 张　宁， 何国田

(1.长春理工大学光电工程学院，吉林长春 130022； 2.中国科学院重庆绿色智能技术研究院机器人中心，重庆 400700)

梯田的无人机械化种植是我国现代化农业发展的难题，自动转向控制技术是在梯田中实现自主导航、精细耕作的关键环节，无人微耕机的自动转向控制器对实现梯田的精细化、现代化种植有重要意义。

目前，国内外对于无人农用机械的研究方向主要针对于大型农用机械。使用的控制算法主要包括PID控制、模糊控制、神经网络控制等。美国Qiu等使用加入了前馈的FPID算法设计了拖拉机电液转向系统[1]。张美娜等针对农用机械的PID控制算法进行了理论分析[2]，黎永键等针对东方红拖拉机的自动转向控制进行了设计和试验[3]，谢斌等针对电动拖拉机的驱动器进行设计并进行了室内试验[4]，宋春月使用GPS和惯导实现了对无人拖拉机的航向控制[5]。但是无人微耕机的研究尚处于遥控式微耕机阶段，丁向美使用ARM芯片设计了微耕机的机上部分和遥操作手持端[6]，通过遥操作控制微耕机的转向。

以上研究使用的控制算法主要针对无人拖拉机进行设计，并不适应于机械结构简单的微耕机，因此，本研究针对无人微耕机单独进行自动转向控制器的设计，采用逆模型-神经网络算法在外环控制转向角度、模糊控制算法在内环控制角速度，使微耕机平稳达到目标角度。

1　自动转向控制器模型

1.1　角度控制模型

微耕机受结构限制，车轮与输入轴间不发生偏转，因此利用差速原理，采用左右输出轮轴各安装电磁离合器的形式实现转向功能，如图1-a所示。通过两轮的速度差实现转向的目的。现假定左轮速度为VL，右轮速度为VR，沿着车辆纵轴线中心的速度为VA，两轮的速度差为ΔA，左右两轮轮距为L，旋转角度为θ。

当假定左转时，车辆的旋转角速度为

(1)

中心线速度为

(2)

车辆的瞬时速度V为

(3)

旋转角度θ为

(4)

根据三角形相似定理可知：

(5)

式中：R为转弯半径。

由式(5)可知，在轮距L为定值时，转弯半径大小与转向时的速度(如VR)及两轮的速度差ΔV有关。此时，左轴电磁离合器结合，左轮可取VL=0，最小转弯半径R为L。同理，当右转时，右轴电磁离合器结合，右轮可取VR=0，最小转弯半径R为L。又由差速器原理知，左转时，VR=2VA，右转时，VL=2VA，由公式(4)得转向角度θ为

(6)

由公式(6)可知，在速度一定的条件下，转向角度与电磁离合器的关闭时间有关，通过控制电磁离合器的关闭时间来控制转角。

1.2　速度控制模型

无人微耕机的油门控制原理如图2所示，根据转矩生成过程，结合喷油量，运用热力学理论，可以计算发动机的指示功率：

Pi=Hμηimf。

(7)

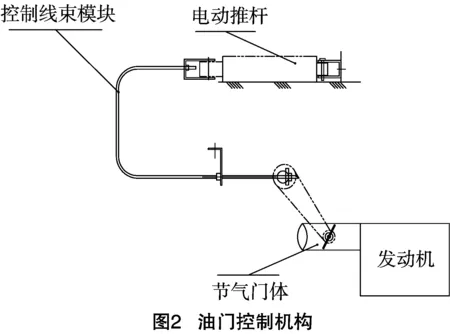
式中：Hμ是燃烧低热值，ηi是指示热效率，mf进入气缸的燃油流量。

从而发动机平均指示转矩为

(8)

式中：w是发动机的转速，考虑工作过程的泵气产生的转矩损失TP，曲轴转动产生的摩擦转矩损失Tf，可得到平均有效转矩Te：

Te=Ti-TP-Tf。

(9)

由公式(8)和公式(9)可推导出：

Pi=(Te+TP+Tf)w⟹Hμηimf=(Te+TP+Tf)w。

(10)

由投影定理可得：

mf=m0s0(1-cosθ)。

(11)

式中：θ取0～90°，m0为单位面积的燃油流量，s0为节气门板面积。

引入电动推杆后：

mf=m0s0(1-cosθkθL)。

(12)

式中：kθ为电推杆与油门转角间对应的比例常数，L为电动推杆的运动行程。

从而，综上所述有：

(13)

由公式(13)可知，在油门开度范围内，且有效转矩Te、泵气损失转矩Tp、摩擦转矩损失Tf不变时，若电动推杆行程L增加，则发动机的转速w增加，因此可通过控制推杆的行程来控制发动机的输出转速，从而控制转动角速度。

2　自动转向控制器设计

2.1　逆模型-神经网络控制算法设计

考虑到转向控制器的非线性，本研究设计的转向控制器通过双闭环实现角度控制，提高了控制精度，控制原理如图3所示。同时，为提高控制器对复杂环境的适应性，使用逆模型-神经网络算法作为外环实现角度的控制，内环通过模糊控制算法实现角速度的控制。

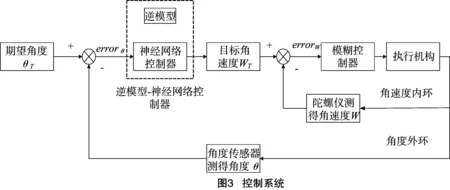
无人微耕机实际工作时，期望角度先输入到逆模型中计算得到补偿量，同时单神经元自适应神经网络控制器根据期望转角计算出目标角速度，用逆模型的补偿量进行修正，输出给内环，内环的模糊控制算法通过目标加速度解算出推杆的行程和挡位的大小，从而实现动作。角度传感器采集微耕机的实际转角，与期望转角求差，作为导师信号对单神经元网络进行训练，从而提高了算法的自适应能力。

在逆模型-神经网络模型中，神经网络模型使用的是单神经元自适应PID算法，把图3中的内环和执行机构简化得到单神经元自适应PID控制结构[7]，如图4所示，根据反馈的角度θ与期望角度θT得到PID算法的比例项xp、积分项xi、微分项xd：

errork=θT-θ；

(14)

xp=errork-errork-1；

(15)

xi=errork；

(16)

xd=errork-2errork-1+errork-1。

(17)

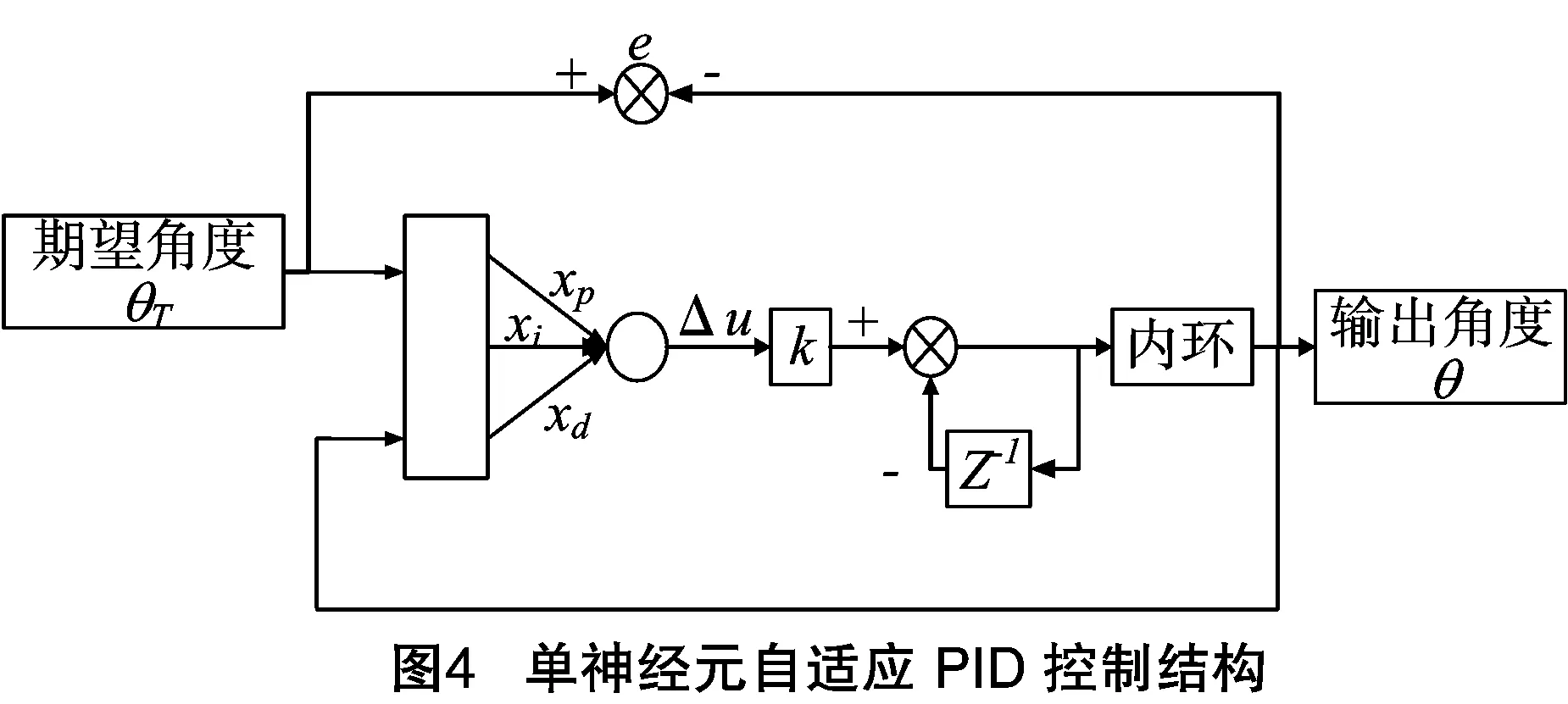
根据增量式PID算法公式有：

Δuk=kpxp+kixi+kdxd。

(18)

式中：kp、ki、kd分别表示比例系数、积分系数、微分系数，Δuk表示k时刻的控制量。

使用改进型学习规则的单神经元学习方式：

(19)

Δerrork=errork-2errork-1+errork-2；

(20)

wp,i,d=ηerrorkΔerrorkΔuk-1。

(21)

式中：wp、wi、wd分别表示kp、ki、kd的权重，η表示学习率。

单神经元通过更改加权系数wp、wi、wd来间接调节kp、ki、kd，针对加权系数的学习单神经元有Hebb学习规则、delta学习规则、改进的学习规则3种学习规则，传统方法仅仅使用Δerrork进行学习，没有最大化利用误差信息，本研究使用改进的学习规则，使用Δerrork和errork进行神经元的训练，最大化提取误差信息，提高神经网络的训练速度和准确度，提高了算法的动态响应能力。

Hebb学习规则：

wp,i,d=ηerrorkΔuk-1xp,i,d。

(22)

delta学习规则：

wp,i,d=ηerrorkΔuk-1。

(23)

本研究使用的改进学习规则：

wp,i,d=ηerrorkΔerrorkΔuk-1。

(24)

逆模型使用BP神经网络算法对神经网络模型进行修正，BP神经网络使用工作信号正向传播、误差反向传播的工作方式。本研究使用的控制芯片是STM32，因此出于减小运算量的考虑使用3个隐层的BP神经网络建立逆模型，预先采集单神经元自适应PID控制器实际输出结果和微耕机的实际转角作为逆模型的训练数据，使用微耕机的实际角度作为逆模型的输入数据，逆模型计算得到预测的输出结果，使用预测的输出结果与微耕机的实际转角之差作为导师信号对逆模型进行训练与学习(图5)。

2.2　模糊控制算法设计

无人微耕机耕作时最大行走速度为0.3 m/s，转弯半径L=1 m，由公式(6)得转向角速度w=0.6 rad/s=34°/s，因此

模糊控制算法中的目标角速度errorw的论域为[-34，34]，涵盖errorw变化范围的F子集为PB(正快)、PM(正中)、PS(正慢)、Z(零)、NB(负快)、NM(负中)、NS(负慢)，其中Z(零)表示微耕机不进行转向动作，其隶属度函数如图6-a所示。为提高控制精度引入Δerrorw=errorwk-errorwk-1，其论域为[-34，34]，涵盖Δerrorw变化范围的F子集为PB(正快)、PM(正中)、PS(正慢)、Z(零)、NB(负快)、NM(负中)、NS(负慢)，其隶属度函数如图6-b所示。推杆最大行程为30 cm，微耕机运行过程中的油门需要保持最低开度，由试验得到此时推杆行程为10 cm，因此推杆行程的论域为[10，30]，使用5等分的F子集涵盖推杆行程变化范围：B(长)、MB(较长)、M(中)、MS(较短)、Z(零)，其中Z(零)表示推杆位于10 cm处，其隶属度函数如图6-c所示。根据无人微耕机的控制经验，确定模糊控制规则，如图7-a所示。最终输出结果如图7-b所示。

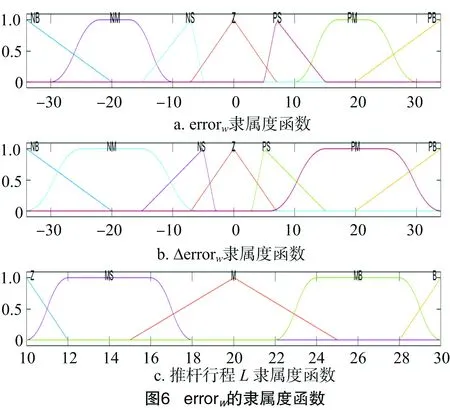
3　试验结果与分析

3.1　算法仿真试验

试验目的：对于已建立的转向系统模型，使用Matlab软件通过仿真试验的方法验证控制器原理上的可行性。

试验方法：输入信号为25°方波信号、正弦信号和三角波信号，使用Matlab辨识被控对象模型，使用M语言描述逆模型-神经网络控制算法和模糊控制算法，得到整体仿真模型，运行M文件得到仿真结果。

试验结果：如图8所示，该控制器对阶跃信号、正弦信号、三角波信号在原理上的跟踪性能良好，其中三角波信号在 0～1 s 处震荡，通过神经网络控制器学习之后，震荡减小，该控制器具有理论可行性。

3.2　实际转向信号跟踪实验

试验目的：验证本研究设计的控制器在实际环境中能有效地控制转向机构跟踪控制系统的指令达到目标角度。

试验方法：上位机发送指令方波信号，该信号为10°阶跃信号，运行本研究设计的控制方法得到数据，使用Origin得到响应曲线。

试验结果：图9所示为方波信号的跟踪结果，实际曲线与输入方波信号有很好的一致性，最大误差为5°，平均误差为0.1°，延时时间为0.28 s。由图10可知，正弦信号最大误差为7°，平均误差为1.8°，该控制器对于正弦信号的跟踪在前 1 s 有较大的震荡，2 s以后误差趋于稳定。由图11可知，三角信号最大误差为7°，平均误差为0.8°，在三角信号的波峰和波谷处，误差有抖动。

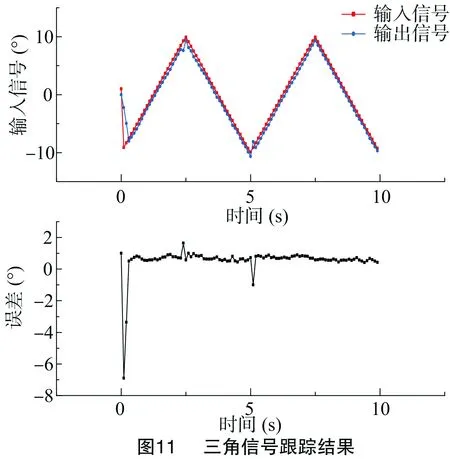
结合以上分析可知，该控制器对于方波信号跟踪良好，对于三角信号和正弦信号，第1次输入有较大的误差，之后的波形可以很好地跟随输入信号，误差平缓趋于稳定。

4　结论

与前人针对于拖拉机设计的PID控制器相比，本研究针对无人微耕机设计了专用的双闭环转向控制器，转向角度作为外环使用神经网络控制，转向速度作为内环使用模糊控制，使微耕机平稳转向目标角度，提出了神经网络和模糊控制的双闭环控制模型适应复杂多变的农业环境，逆模型神经网络修正单神经元自适应PID算法的误差，针对STM32进行了算法优化，降低了算法复杂度和成本。样机试验结果表明，方波信号跟踪平均误差为0.1°，延时时间为0.28 s，正弦信号跟踪平均误差为2.2°，三角信号跟踪平均误差为0.8°，但在神经网络控制器学习时间内。输出误差较大需进一步优化算法。因此本研究设计的控制器满足农业环境应用要求，并为进一步试验提供平台。

参考文献：

[1]Qiu H，Zhang Q. Feedforward-plus-proportional-integral-derivative controller for an off-road vehicle electrohydraulic steering system[J]. Proceedings of the Institution of Mechanical Engineers Part D-Journal of Automobile Engineering，2003，217(5)：375-382.

[2]张美娜，林相泽，丁永前，等. 基于性能指标的农用车辆路径跟踪控制器设计[J]. 农业工程学报，2012，28(9)：40-46.

[3]黎永键，赵祚喜，黄培奎，等. 东方红拖拉机自动转向控制器设计及试验[J]. 农业工程学报，2015，31(增刊2)：93-99.

[4]谢斌，张超，毛恩荣，等. 基于myRIO的电动拖拉机驱动控制器设计与室内试验[J]. 农业工程学报，2015，31(18)：55-62.

[5]宋春月. 无人驾驶拖拉机控制系统设计研究[D]. 上海：上海工程技术大学，2015.

[6]丁向美. 基于ARM的微耕机远程控制系统的研究[D]. 重庆：西南大学，2011.

[7]刘金琨. 先进PID控制MATLAB仿真[M]. 北京：电子工业出版社，2011.