铅-磁流变阻尼器在减震结构中的位置优化

张香成， 陈　娜， 罗　芳， 赵　军， 徐赵东

(1.郑州大学 力学与工程科学学院，河南 郑州 450001； 2.郑州财经学院，河南 郑州 450000； 3.东南大学 土木工程学院，江苏 南京 210096)

0　引言

铅-磁流变阻尼器(lead magnetroheological damper，LMRD)是本课题组研发的一种半主动控制装置，阻尼力可调，耗能能力强，所需电源较少，控制系统相对简单，可靠性高[1-2].研究表明：结构的半主动减震控制效果既与装置的力学性能和控制算法有关又与装置的位置有关.近年来，国外关于磁流变半主动控制装置优化布置的研究已取得一些成果[3-5].国内徐龙河等对磁流变阻尼器在结构中的位置进行了优化[6]，贝伟明等基于改进遗传算法对磁流变阻尼器在高层建筑结构中的位置进行了优化[7]，阎石等对磁流变阻尼器位置优化方法进行了对比研究[8]，展猛等在空间桁架模型中对不同数量的阻尼器进行了位置优化[9]，闫维明等对不规则结构中阻尼器的参数和位置进行了优化[10].

为更好地实现加入LMRD的减震效果，以撤掉LMRD产生的受控结构最优二次型性能指标损失量作为优化目标，在El-Centro波、Taft波和人工波作用下，采用MATLAB软件，对钢筋混凝土框架结构在LMRD最优布置、任意布置和未布置多种工况下进行编程和仿真分析，最后将计算结果进行对比分析.

1　LMRD结构及半主动控制算法

1.1　LMRD减震结构的运动微分方程

在地震作用下，LMRD受控结构的动力学方程为：

(1)

1.2　半主动控制算法

结构中拟设置的LMRD如图1所示.

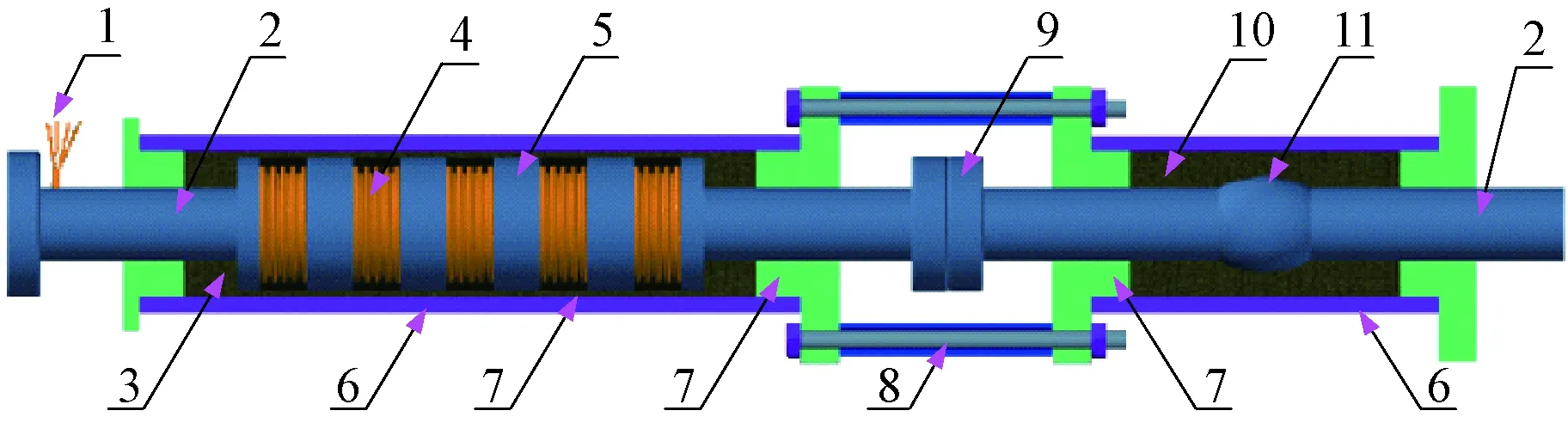
1.导线；2.活塞杆；3.磁流变液；4.线圈；5.活塞；6.缸桶；7.盖板；8.钢管；9.连接法兰；10.金属铅；11.轴凸图1　LMRD结构装配图Fig.1　Structure assembly diagram of LMRD

在频率为0.1 Hz,振幅10 mm的正弦波激励下，LMRD在0、0.6、1.2、1.8、2.4 A 5级电流下的最大阻尼力测试值分别为124.22、194.90、249.38、278.19和284.49 kN.

采用线性二次型调节器算法[11-12]计算结构中LMRD的最优控制力U(t)，

(2)

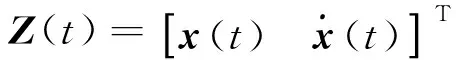
定义系统的二次型性能指标最小为控制目标，

(3)

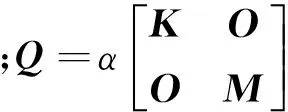
U(t)=-R-1BTPZ(t)=GZ(t)，

(4)

式中：G为增益矩阵；P由Riccati方程求出：

PA-PBR-1BTP+ATP+Q=0.

(5)

最优控制的结果与Q、R中α、β的取值有关.

由于LMRD阻尼力具有一定范围.因此，需对式(4)的最优控制力U(t)进行调整，以第i个LMRD为例，

(6)

式中：Fi为LMRD的控制力；Fi,min为LMRD的最小阻尼力；Fi,max为最大阻尼力；Ui为最优阻尼力；ui为LMRD两端的位移.

2　优化目标

将式(4)代入式(2)和式(3)得：

(7)

(8)

式(7)可以分解为：

(9)

ψ=exp[(A-BG)t]，

(10)

当撤掉第i个阻尼器时，位置指示矩阵B将产生一损失量ΔBi，同时导致二次型性能指标产生损失量ΔJi，根据泰勒展开式，略去高阶微量，可以求得撤掉第i个阻尼器时受控结构的二次型性能指标损失量为：

ΔJi=-tr[(R0+P)SmΔBiG]，

(11)

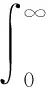
式(11)反映了第i个LMRD对结构最优控制的灵敏度.ΔJi越小，说明撤掉的第i个LMRD对受控结构最优控制不敏感或不重要，反之则越敏感或越重要.因此可根据撤掉阻尼器时得到的ΔJi，对每个LMRD在受控结构中的重要性进行排序.此外，从式(11)可以看出，ΔJi是在假定受控结构处于弹性状态，并且撤掉LMRD后受控结构最优反馈增益矩阵G不变的条件下得到的.

3　算例及优化过程

采用一栋十二层钢筋混凝土一榀框架对LMRD进行位置优化.结构1～2层柱截面尺寸为0.7 m×0.7 m；3～8层柱截面尺寸为0.6 m×0.6 m；9～12层柱截面尺寸为0.5 m×0.5 m；边跨长7.2 m，梁截面尺寸为0.3 m×0.6 m；中间跨长5.4 m，梁截面尺寸0.25 m×0.5 m，结构层高见图2，柱底与基础刚性连接.

地震波选用El-Centro波(1940年南北向)、Taft波(1952年东西向)两条强震记录和人工波，均持时20 s，地震加速度峰值为400 gal.人工波采用三角级数法合成，功率谱密度函数采用金井清模型[13]，模型参数ωg=15、ζg=0.6、S0=74.4，合成的波形见图3.

4　优化结果分析

用MATLAB编制了未控及受控结构的弹性时程分析程序，选用Wilson-θ法求解结构的动力学方程，并取θ=1.4.通过程序试算，在3条地震波下，控制算法Q、R矩阵中α=100、β=3×10-6.

在上述3条地震波下依次撤掉各层LMRD，然后根据式(11)计算ΔJi，并根据计算结果绘制

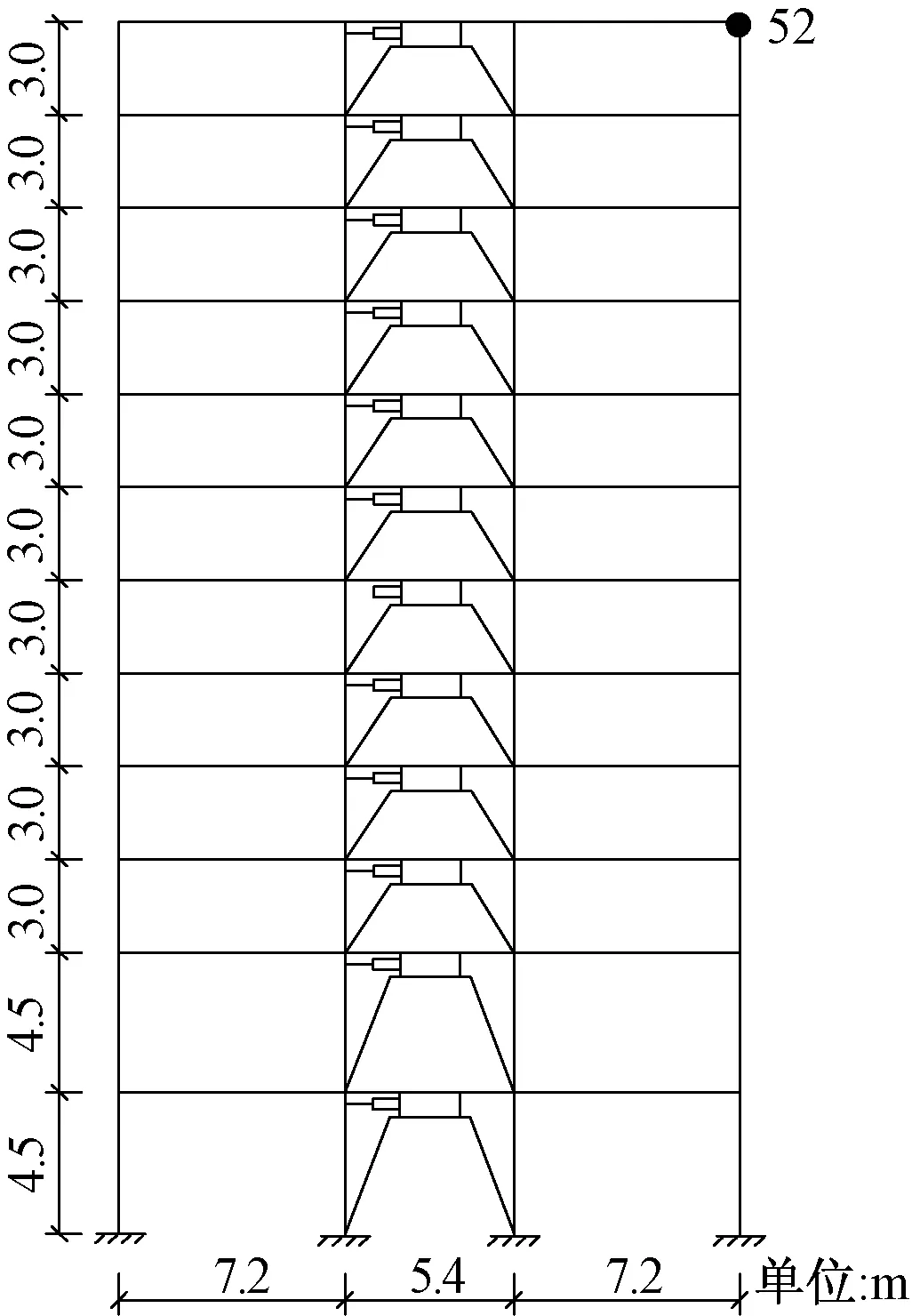
图2　LMRD在钢筋混凝土框架结构中的位置Fig.2　Location of LMRD in reinforced concrete frame structure

不同地震波下各层阻尼器对结构最优控制的灵敏

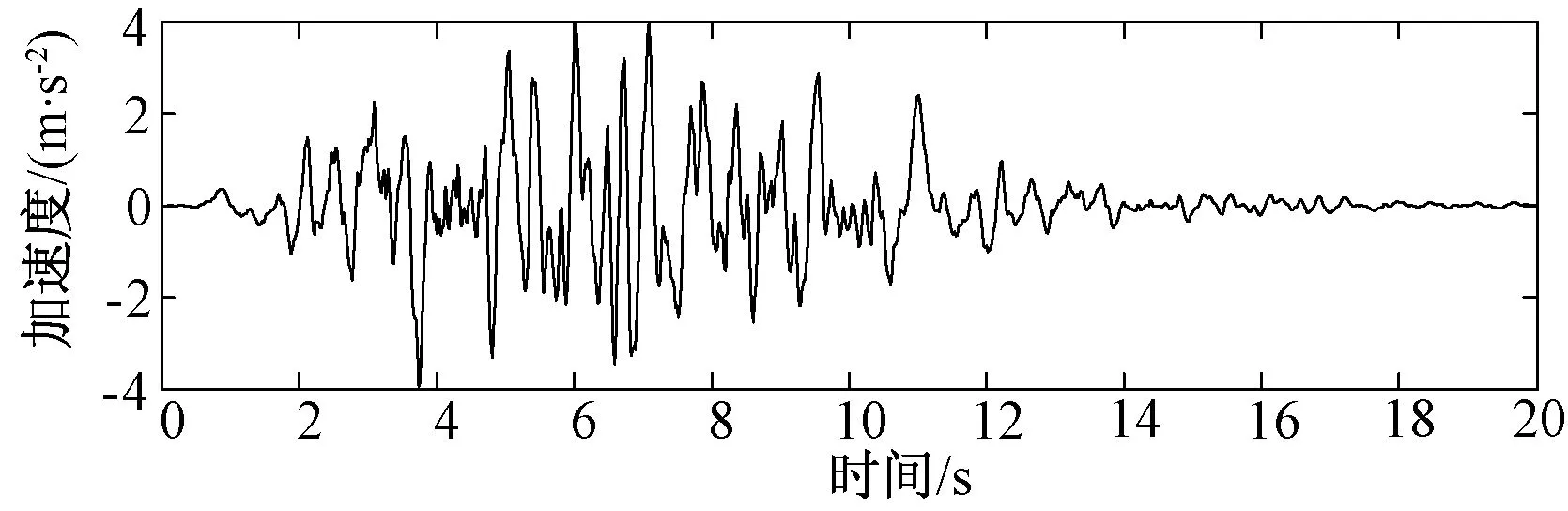
图3　合成的人工地震波Fig.3　The synthesis of artificial seismic wave

度柱状图，如图4.

从图4中可以看出，当撤掉同一阻尼器时，虽然受控结构在不同地震波激励下得到的二次型性能指标损失量的大小相差很大，但在同一地震波下LMRD对结构最优控制的敏感性顺序基本相同.这是因为不同地震波在整个频率段内的能量密度有所差异，它输入到特定受控结构的能量有多有少，并且结构振动能量的总体分布跟结构自身参数有关，并不因地震波的不同而发生较大改变.

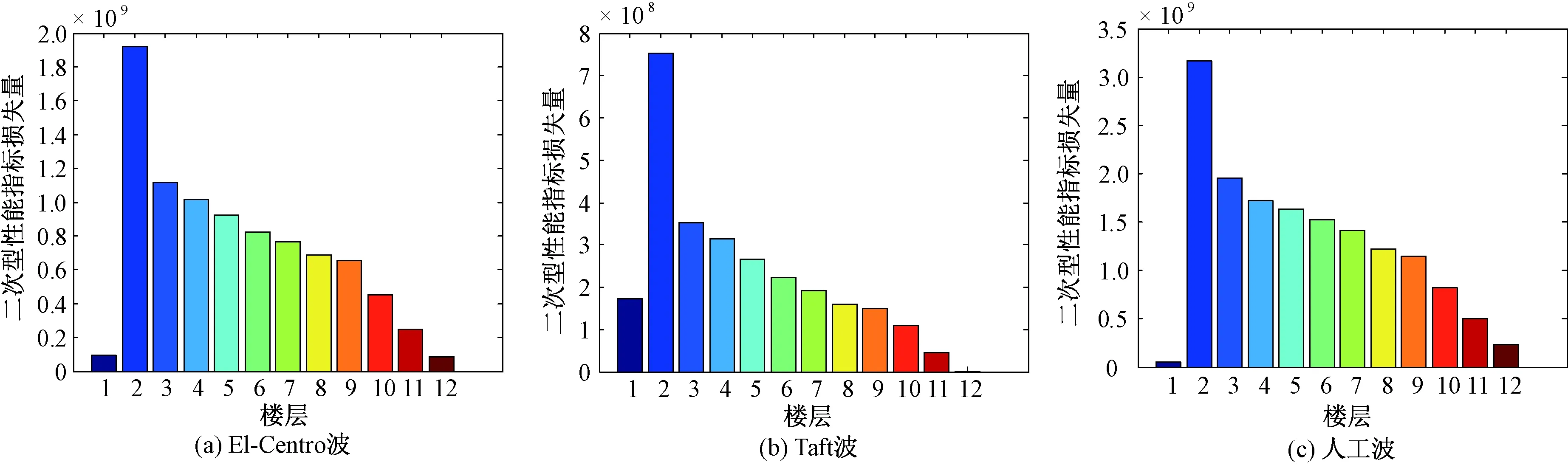
图4　不同地震波下阻尼器对结构最优控制的灵敏度Fig.4　The sensitivity of damper on structural optimal control under different seismic waves

此外，在El-Centro波作用下，撤掉各层LMRD时受控结构二次型性能指标损失量从大到小顺序是：2层、3层、4层、5层、6层、7层、8层、9层、10层、11层、1层、12层.在Taft波和人工波作用下，除1层外，撤掉其他层LMRD时受控结构二次型性能指标损失量大小顺序与El-Centro波作用下的顺序相同.阻尼器对受控结构最优控制的敏感性大致规律为：除1层外，结构下部的阻尼器对受控结构最优控制的灵敏度较大，结构上部的阻尼器对受控结构最优控制的灵敏度较小.这是因为在地震作用下，框架结构以剪切变形为主，下部结构的剪切变形一般大于上部结构的剪切变形，因此位于结构下部的阻尼器能更好地起到耗能减震作用，其对受控结构最优控制的灵敏度也就越大.由于算例假定1层柱底与基础刚性连接，因此1层结构的剪切变形计算结果偏小，进而导致该层阻尼器对受控结构最优控制的灵敏度变小.

5　优化结果验证

根据优化结果，按表1列出的工况在结构中布置LMRD，每种工况阻尼器的个数均为6个.在上述3条地震波激励下对结构在阻尼器最优布置、任意布置1、任意布置2和未布置(工况4)工况下进行时程分析，并将计算结果进行了对比分析.

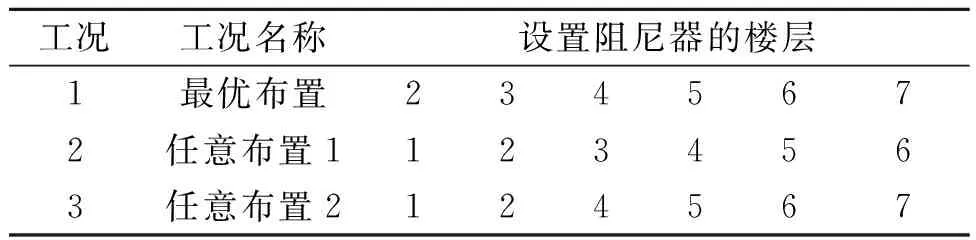
表1　不同工况下LMRD的布置位置

图5～图7分别为El-Centro波、Taft波和人工波激励时，结构在不同工况下顶层52号节点的水平位移和加速度时程响应曲线.

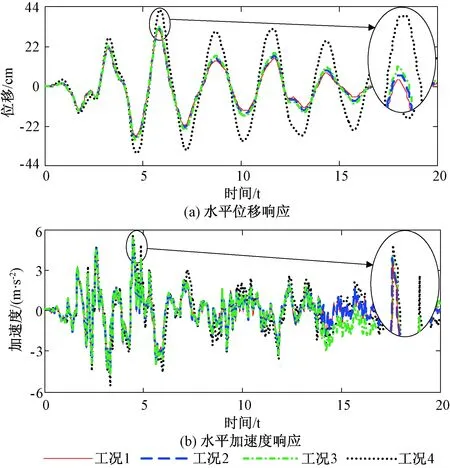
图5　El-Centro波下结构顶层52号节点的动力响应Fig.5　Dynamic responses of the No. 52 node on top-floor under El-Centro wave

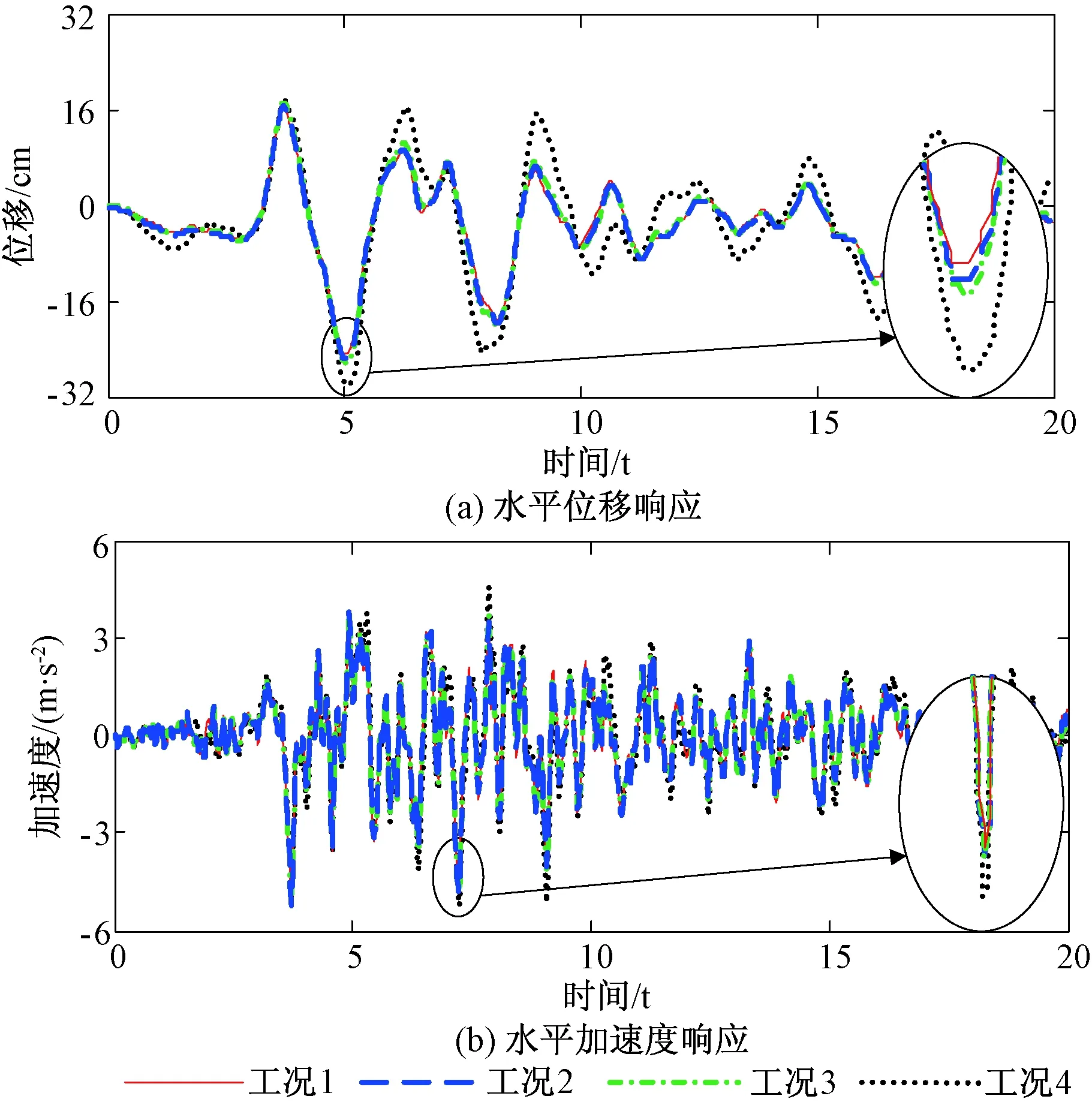
图6　Taft波下结构顶层52号节点的动力响应Fig.6　Dynamic responses of the No. 52 node on top-floor under Taft wave

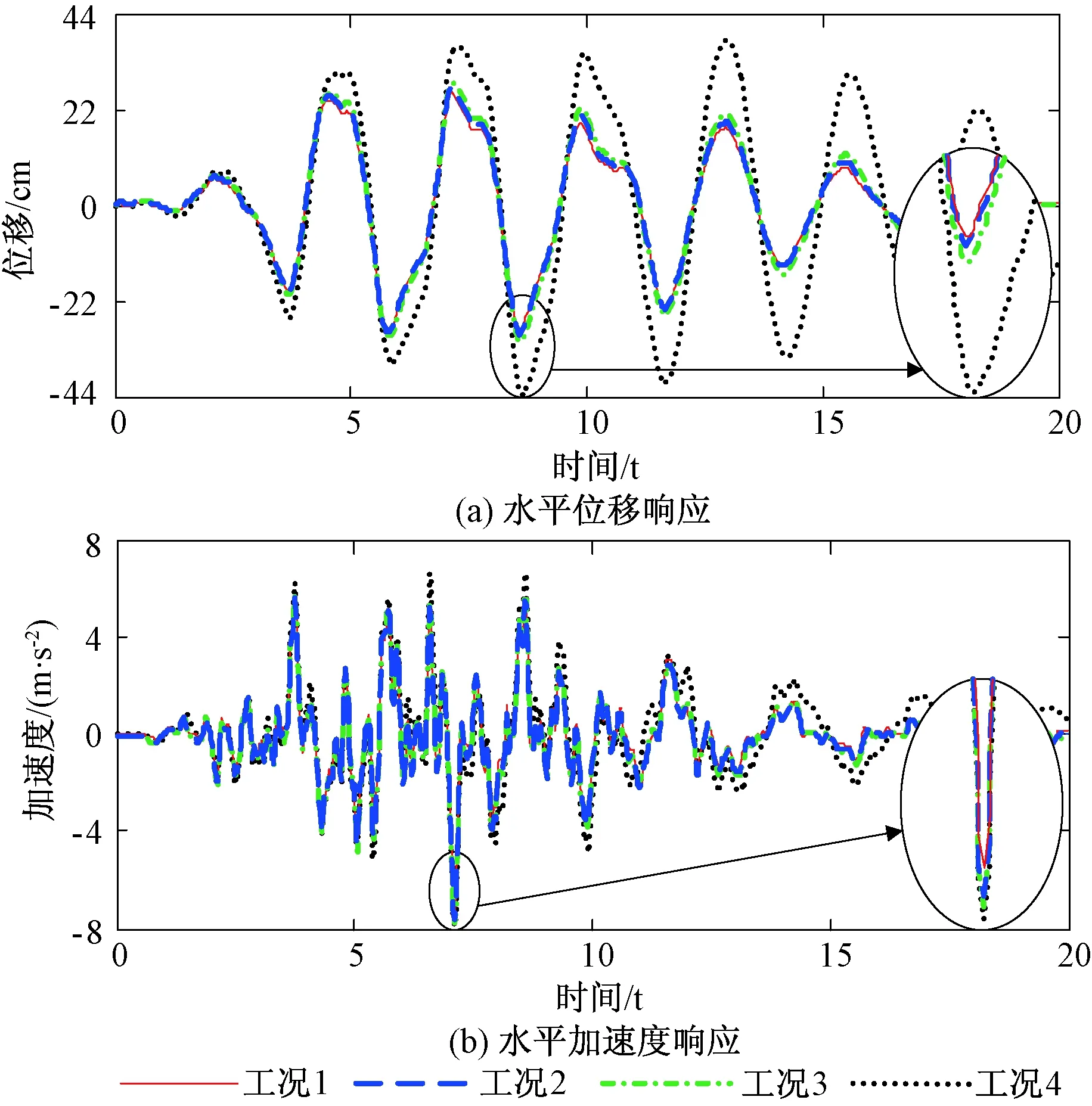
图7　人工波下结构顶层52号节点的动力响应Fig.7　Dynamic responses of the No. 52 node on top-floor under Artificial wave

从图5(a)～图7(a)可以看出，在整个地震持续时间内，设置LMRD结构顶层52号节点的水平位移较无控结构明显减小.在设置LMRD的结构中，按工况1布置LMRD时结构顶层52号节点的水平位移响应在整个地震持续时间内最小，然后分别是工况2和工况3.在El-Centro波作用下，工况1、工况2、工况3和工况4对应的52号节点最大位移响应分别为31.00、31.94、33.15和41.80 cm.在Taft波作用下，工况1、工况2、工况3和工况4对应的52号节点最大位移响应分别为25.06、25.54、26.27和30.34 cm.在人工波作用下，工况1、工况2、工况3和工况4对应的52号节点最大位移响应分别为29.07、30.24、32.05和43.55 cm.这说明按优化结果在结构中布置LMRD可以使顶层52号节点的位移时程响应获得最优的减震控制效果.

从图5(b)～图7(b)可以看出，在整个地震持续时间内，所有工况对应的结构顶层52号节点的水平加速度基本相同.在El-Centro波作用下，工况1、工况2、工况3和工况4对应的52号节点最大加速度响应分别为5.16、5.23、5.22和5.56 m/s2.在Taft波作用下，工况1、工况2、工况3和工况4对应的52号节点最大加速度响应分别为5.27、5.23、5.23和5.24 m/s2.在人工波作用下，工况1、工况2、工况3和工况4对应的52号节点最大加速度响应分别为7.33、7.55、7.65和7.95 m/s2.

表2～表4分别为El-Centro波、Taft波和人工波激励时，不同工况对应的楼层最大位移和加速度.可以看出,在El-Centro波、Taft波和人工波作用下，与未控结构(工况4)相比，加入LMRD后结构各层的最大位移均得到不同程度的降低，其中，工况1对应的结构每层最大位移响应降幅最大，其次结构每层最大位移响应降幅较大的分别是工况2和工况3.这说明按优化结果在结构中布置LMRD可以使结构的位移响应获得最优的减震控制效果.此外，从表2～表4中还可以看出：在3条地震波作用下，与未控结构(工况4)相比，加入LMRD后结构各层的最大加速度响应变化并不明显，且无规律可循.

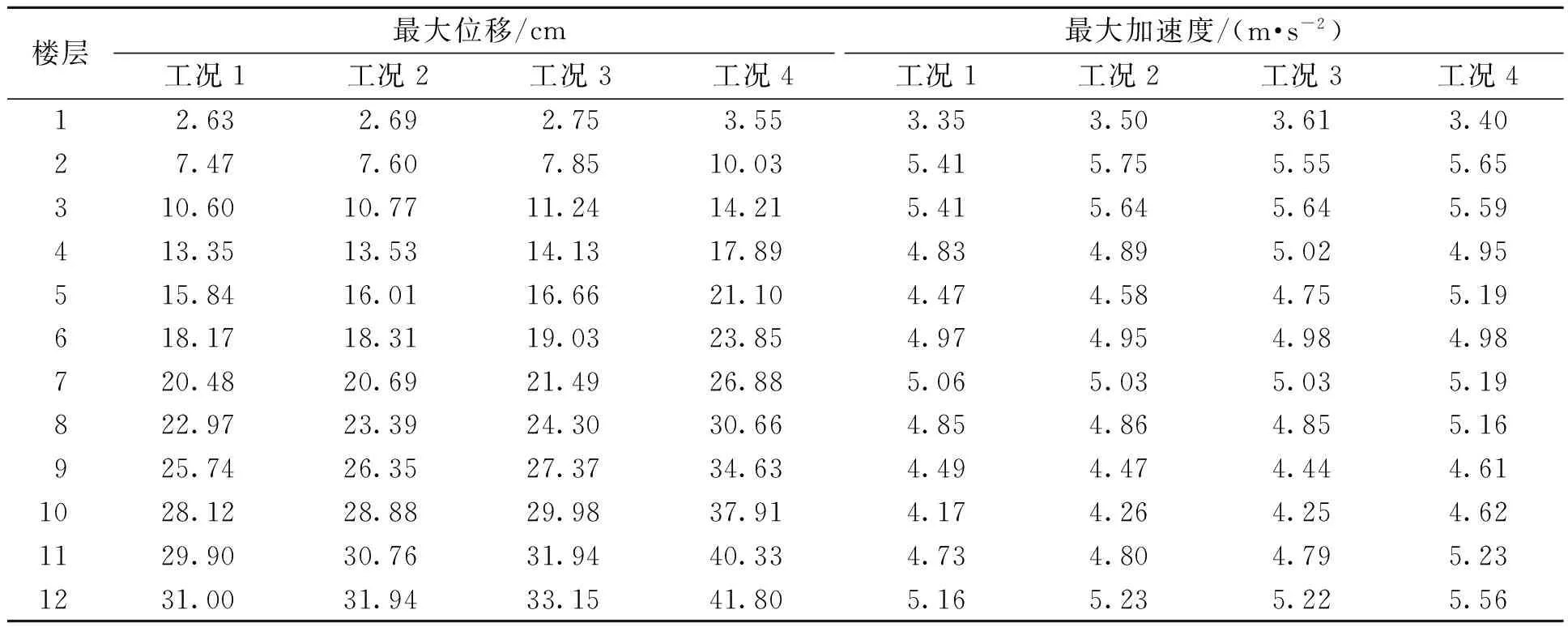
表2　El-Centro波下不同工况对应的楼层最大动力响应

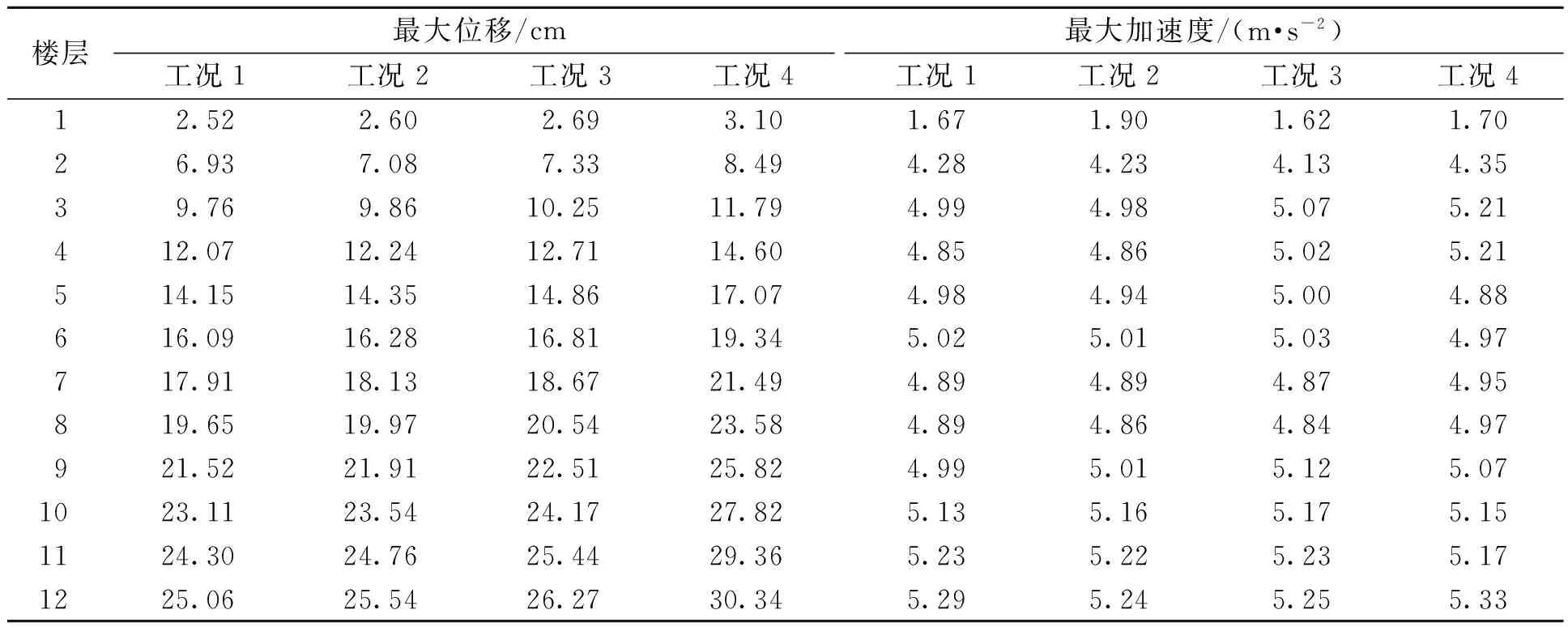
表3　Taft波下不同工况对应的楼层最大动力响应

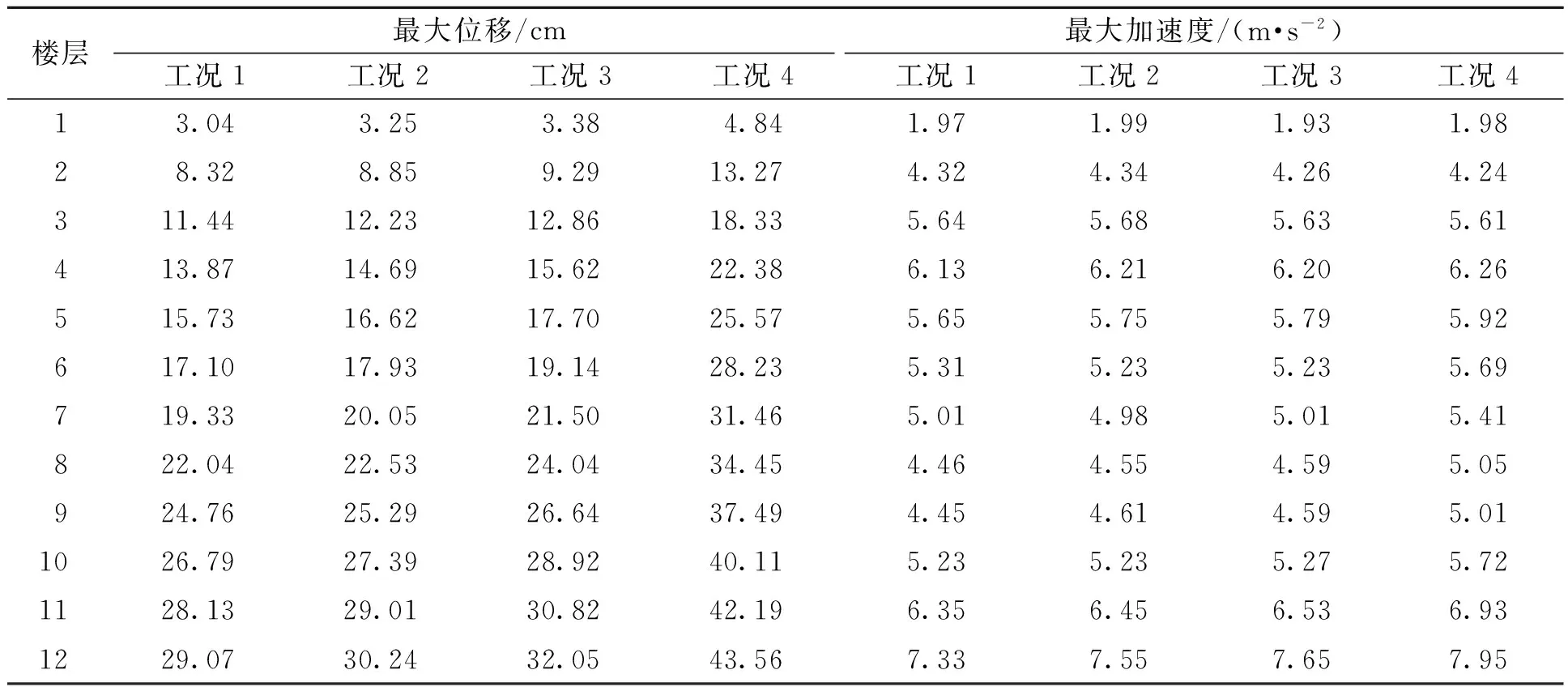
表4　人工波下不同工况对应的楼层最大动力响应

6　结论

(1)LMRD对地震作用下结构的水平位移响应控制效果较为明显，但对加速度响应控制效果不明显.

(2)以撤掉LMRD产生的结构最优二次型性能指标损失量作为优化目标时，LMRD在结构中的最优位置取决于结构自身参数，与地震波类型关系不大.

(3)与任意布置相比，LMRD采用最优布置(工况1)时，可以最大限度降低结构的水平位移响应，说明优化结果准确、有效.

参考文献：

[1]ZHANG X C, XU Z D. Testing and modeling of a CLEMR damper and its application in structural vibration reduction[J]. Nonlinear dynamics, 2012, 70(2): 1575-1588.

[2]张香成, 张旭, 徐赵东, 等. 配有铅-磁流变阻尼器的高层RC框架结构非线性动力分析[J]. 建筑结构学报, 2016, 37(4): 119-125.

[3]TAKEWAKI I. Optimal damper placement for minimum transfer function[J]. Earthquake engineering and structural dynamics, 1997, 26(11): 1113-1124.

[4]POHORYLES D A, DUFFOUR P. Adaptive control of structures under dynamic excitation using magnetorheological dampers: an improved clipped-optimal control algorithm[J]. Journal of vibration and control, 2015,

21(13): 2569-2582.

[5]ASKARI M, LI J C, SAMALI B. Cost-effective multi-objective optimal positioning of magnetorheological dampers and active actuators in large nonlinear structures[J]. Journal of intelligent material systems and structures, 2017, 28(2): 230-253.

[6]贝伟明, 李宏男. 磁流变阻尼器在结构减震控制中的位置优化研究[J]. 工程抗震与加固改造, 2006, 28(3): 73-78.

[7]滕军. 相邻结构间控制器位置及控制律的降阶优化方法研究[J]. 建筑结构学报, 2003, 24(4): 17-24.

[8]阎石, 宁欣, 王宁伟. 磁流变阻尼器在受控结构中的优化布置[J]. 地震工程与工程振动, 2004, 24(3):175-178.

[9]展猛, 王社良, 朱熹育, 等. 空间桁架模型压电摩擦阻尼器半主动优化控制[J]. 建筑结构学报, 2014, 35(8): 50-56.

[10] 闫维明, 杲晓龙, 谢志强. 基于复杂三维有限元模型和鱼群算法的平面不规则结构中位移型阻尼器参数和位置的优化方法[J]. 工程力学, 2016, 33(9): 155-163.

[11] 欧进萍. 结构振动控制-主动、半主动和智能控制[M]. 北京: 科学出版社, 2003.

[12] 刘本学, 蔺超云, 郭沛东, 等. 基于MATLAB的汽车线性最优控制主动悬架仿真研究[J]. 郑州大学学报(工学版), 2016, 37(5): 72-76.

[13] 彭凌云, 周锡元, 李小军. 对已有强震地面运动功率谱模型的改进[J]. 北京工业大学学报, 2011, 37(3): 388-394.