目标体位置对井地电阻率反演成像的影响研究

丁尚见 雷宛 蒋林城 贾毅 王志文

摘 要：井地电法勘探是通过直流电对地下空间进行研究的方法。本文通过有限单元法完成点源二维直流电法正演数值计算，再应用平滑约束下的最小二乘算法实现“L”型井地直流电阻率反演成像达到探明地下空间电性的目的。通过比对位于不同位置目标体模型的反演成像结果，发现随着目标体距离地面和井孔长度变长，目标体的形态、大小规模、物性都发生较大变化，为实际物探工作中的图件解释具有重要的指导意义。

关键词：井地电法；地下空间；反演成像；目标体位置

中图分类号：P631 文献标识码：A 文章编号：1671-2064（2018）06-0218-02

1 引言

常规直流电法勘探中，点源及测量电极往往布置于地表之上，进而导致成像结果随着埋藏深度变化而变化（安然等，2007）。井地电阻率勘探分别于地表和井中布置电极进行测量的一种直流电法，它能够较清晰勘察井口和地表所包围的一定范围内的地下电性情况。本研究需要数值模拟和电阻率成像两大模块，其中直流电阻率数值模拟现阶段主要使用有限差分算法和有限单元法（黄俊革，2003；吕玉增，2008），由于有限单元法相对前者有着较好精度条件，所以其为本研究所采用。反演成像主要包括线性反演与非线性反演两大类，线性反演为最常使用的一类，本研究采用隶属于线性反演成像中的平滑约束下的最小二乘反演。本文主要研究“L”型井地直流电法勘探中研究范围内各个区域的分辨率问题。

2 反演成像原理

电阻率反演问题是非线性问题，为使成像结果尽量简单光滑，同时为保证反演算法的稳步迭代，将电阻率反演的目标函数分为两部分，表示如下：

ψ=||Wd（Δd-JΔm）||2+λ||CΔm||2 （1）

其中，Wd表示数据权系数矩阵，C表示光滑系数矩阵及模型权系数矩阵，J表示雅克比矩阵，Δd为观测数据的增量，Δm为模型参数增量，λ是光滑因子，用来约束反演结果的光滑程度。

将目标函数（1）式关于Δm求导数并令其等于0，则可得到反演算法的线性方程组如下：

（JTJ+λCTC）Δm=JTΔd （2）

求解上式得Δm，新的模型为：mi+1=mi+Δm （3）

如此循环直至目标函数值小于阀值或者迭代次数达到要求。

3 “L”型井地电法勘探原理

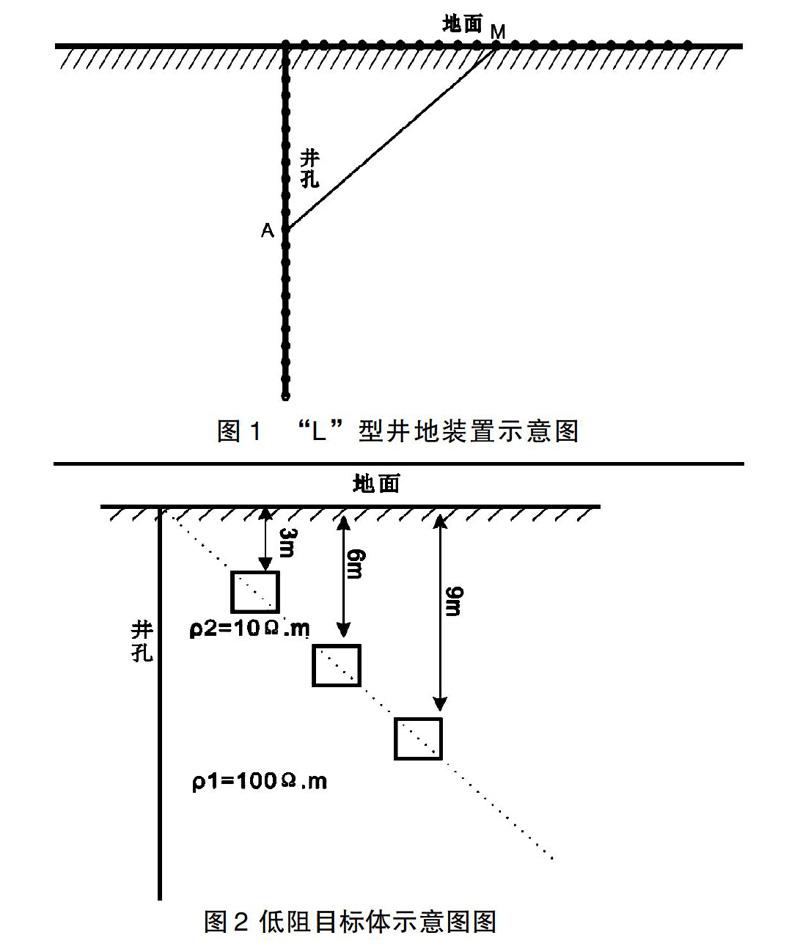
“L”型井地电法主要应用为探测井某一侧的电性分布情况，其分别于地面和井中放置电极进行地面和井中的透射测量，该方法电极分布图如图1。

由于井孔和地面相较，所以井地直流电阻率勘探常使用图1所示的二极装置测量，其测量时在井孔各个电极处供电，然后将地表的电极作为测量电极。再利用所得电位计算视电阻率，其视电阻率计算公式为：

ρs= （4）

上式中ρs为视电阻率，UMA表示在点A供电情况下M点的电位大小，M'为M点关于地面的对称虚源。

4 目标体位置对反演结果影响

常规地面直流电法中提出目标体埋藏深度的增大，反演结果对目标体的分辨率变差。考虑井地直流电法同常规地面直流电法的相似性，本文研究目标体与地面和井孔之间距离的逐渐加大，其反演成像结果的变化结果。因此，设计一套“L”型井地电法观测系统，其中井孔和地表分别布置30根电极，电极距为1m，然后将目标放置于地面和井孔的角平分线进行数值模拟，再将所得视电阻率代入反演系统中成像。具体模型图如图2。

如图2所示，低阻目标体电阻率10Ω.m，围岩电阻率100Ω.m，同时低阻目标体为一边长2m的正方形，其位于角平分线上，边长距离地面距离s分别是3m、6m、9m。对以上模型进行数值模拟得到视电阻率数据，再将视电阻率数据进行反演成像。所得反演成像结果如图3。

反演初始参考模型为测量数据的平均值，图3为目标体在不同位置反演成像结果。图3（a）为目标体距离地表长度s等于3m是的反演，图3（b）和图3（c）则为s分别为6m和9m是的反演成像结果。对比不同位置目标体的反演结果发现，随着距离s的增大，反演结果越难分辨目标体，反演图上的目标体所占区域变大，等值线变稀疏，同时目标体会沿着与地面和井孔相交方向被拉伸。

5 结语

本文采用有限单元法进行数值模拟，再利用基于平滑约束的最小二乘反演对井地直流电阻率数据反演成像，重点论述反演原理和井地直流电法勘探的工作模式，并研究目标体距离井孔和地面的长度大小对反演结果的影响。通过对不同位置目标体的反演结果比对，目标体与地面和井孔距离直接影响反演结果对目标体的反映，随着距离的增大，目标体所处位置等值线将变稀疏，同时沿着一定方向被拉伸，表明在对实际数据反演成像过程中，根据目标的位置设置钻孔，同时在对反演图件的解释时要注意根据位置判断目标体大小规模。

参考文献

[1]安然，李桐林，徐凯军.井地三维电阻率反演研究[J].地球物理學进展，2007，22（1）：247-249.

[2]黄俊革.三维电阻率/极化率有限元正演模拟与反演成像[D].中南大学，2003.

[3]吕玉增.地—井、井—地IP三维快速正反演研究[D].中南大学，2008.

[4]潘克家，王文娟，谭永基，等.基于混合差分进化算法的地球物理线性反演[J].地球物理学报，2009，52（12）：3083-3090.

[5]宋滔，王绪本.点源二维电场正演的一组新的波数[J].地球物理学进展，2014，29（1）：166-171.

[6]万乐.我国南方岩溶石山地区地下水勘查的新方法新技术[D].中国地质大学（武汉），2000.