承力索恒张力架设一次到位的影响因素分析

黄 河



承力索恒张力架设一次到位的影响因素分析

黄 河

以接触网链形悬挂计算理论为基础，详细讨论了承力索恒张力架设施工中的影响因素，得出了承力索在不同情况下的2种安装曲线，以便能够在架线施工中一次到位。

接触网；承力索；架设；一次到位；应用

0 引言

在承力索架设施工中，通常采用小张力或无张力架设，在下锚位置以设计的额定张力下锚。小张力或无张力架设的优点在于架线过程易操控，缺点是下锚张力大，架线过程中易伤线，且在架设接触线和布置吊弦后，由于承力索整体负载变化，引起承力索张力变化，致使承力索补偿装置需重新调整。若以恒张力方式进行承力索架设，则可减小下锚张力，增加施工安全性。若对恒张力进行有效控制，使之达到接触网施工完毕的状态，则可减少后期调整工作量。以恒张力方式架设承力索的关键影响因素包括张力、线索长度、温度、负载变化4个方面。

1 影响因素分析

1.1 当量跨距

在一个锚段内包含了许多不相同的实际跨距l，一般在悬挂点处悬挂的线索可以沿线路方向移动，因此各实际跨距内基本保持相同的张力。其跨距值由下式决定[1]：

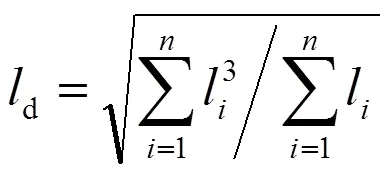
1.2 张力变化的影响

1.2.1 有载承力索张力计算

按照链形接触悬挂的计算理论，当外部环境发生变化，对d内的接触悬挂弛度会产生影响，从而引起线索总长度的变化，其变化量为

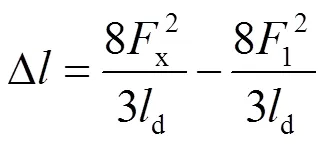
考虑线索的长度变化、温差及新线延伸率，即

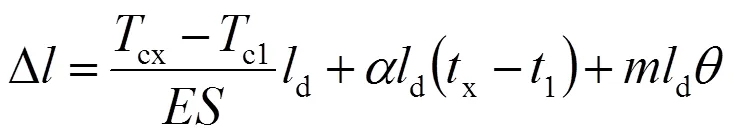
那么，

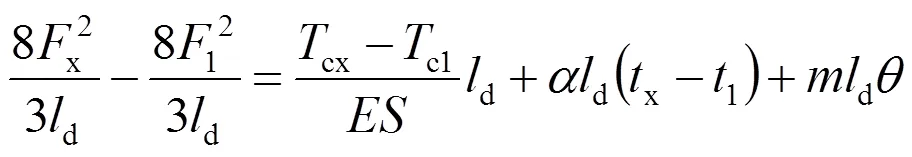
即得到有载承力索的张力普遍方程：

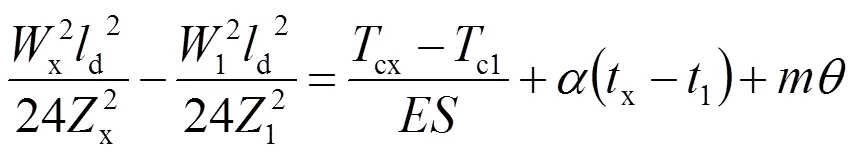
式中，x、1分别为变化后、变化前承力索的跨中弛度，m；cx、1分别为变化后、变化前的承力索张力，kN；x、1分别为变化后、变化前链形悬挂的归算负载，kN/m；x、1分别为变化后、变化前链形悬挂的归算张力，kN；x、1分别为变化后、变化前的温度，℃；为承力索弹性系数，kN/mm2；为计算截面积，mm2；为线索的膨胀系数，1/℃；为新线延伸系数，0≤≤1；为新线延伸率。

式（5）中的x、1及x、1可由下式确定：

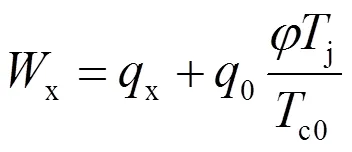
x=cx+Tj；1=cmax+Tj（7）

式中，x、1分别为变化后、变化前的承力索总负载，kN/m；0为无冰、无风时承力索总负载，kN/m；c0为在0温度下承力索的张力，kN；j为接触线张力，kN。

式（6）、式（7）中的值表征接触悬挂的结构特征，称为结构系数，由下式确定：

1.2.2 无载承力索张力计算

对于全补偿链形悬挂的承力索架线，假设：x=c（c为承力索自重，kN/m）；x=cx-（为架线张力，kN）；x=（为架线温度，℃）。设起始条件：1=cdj（cdj为接触悬挂负载，kN/m）；1=c1=c（c为承力索的额定张力，kN）；1=p（p为平均温度，℃），那么，式（5）可写成

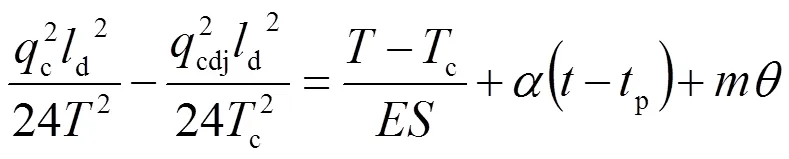
式（9）为无载承力索的张力普遍方程，表征接触悬挂在当量跨距间承力索悬挂负载、温度变化和张力变化的关系。

在式（9）中代入不同的值，即可求得相应温度。根据若干组、数据即可绘出无载承力索的安装曲线=()。

以遂渝铁路为例，遂渝铁路某锚段采用THJ-95+CTHA-120全补偿简单链形接触悬挂，已知：c= 14.7 kN，d= 56.547 m，c= 5.85 N/m，cdj= 16.93 N/m，= 124 kN/mm2，= 95 mm2，= 17.6×10-6-1，p= 20℃，= 2×10-4，= 0.5。将数据代入式（9）可得表1数据，然后由表1绘制出无载承力索安装曲线图，如图1所示。

1.3 张力引起弹性变形对线索长度的影响

当线性力作用于线索时，由于弹性变形，线索长度将发生变化，假如施工时的线性力未超过弹性变形极限，一旦作用力取消，线索会恢复到其原始长度。如果弹性模量（杨氏模量）是已知的，可以计算出弹性变形引起的线索长度变化。当作用于线索的力从0增加到x时，线索长度变化为

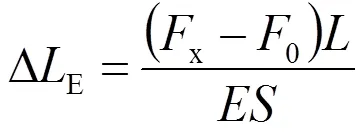
以遂渝铁路半个锚段（750 m）为例，THJ-95承力索张力为10 kN时，其预张长度增加0.58 m。

1.4 温度变化影响

线索的热膨胀也会使线索的长度发生变化，其变化量为

Dw=(x-0) （11）

式中，为线索长度，m；x、0分别为当前温度和起始温度，℃。

仍以遂渝铁路为例，以半个锚段（750 m）进行计算，温度从-30℃升高到70℃时，THJ-95承力索的长度变化量为1.32 m。

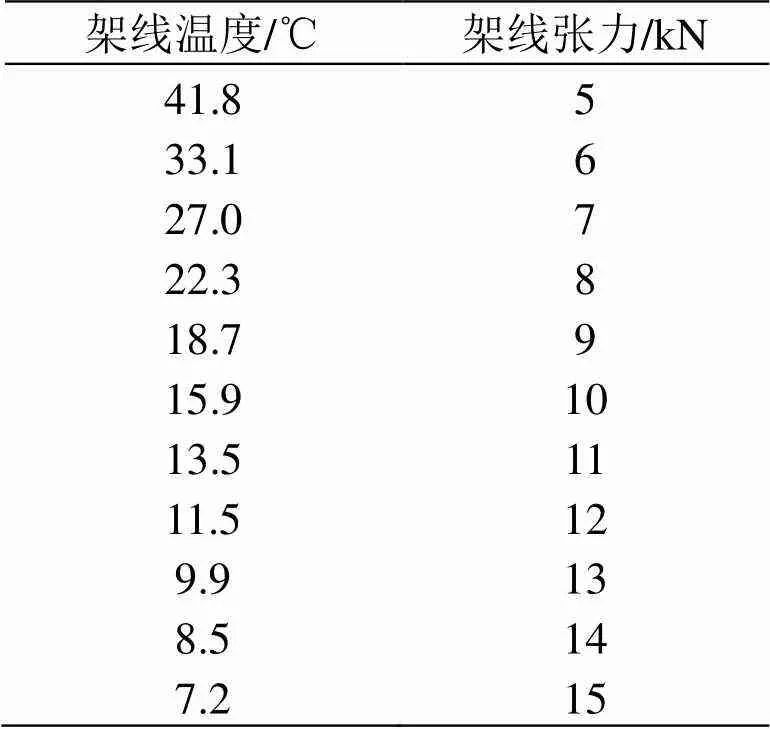
表1 无载承力索安装表

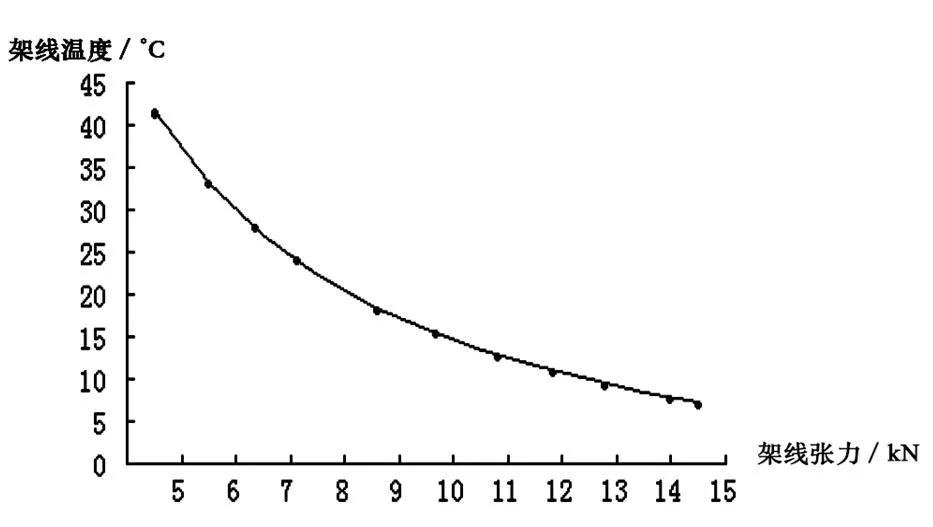
图1 无载承力索安装曲线

1.5 负载变化影响

负载包括线索自重负载和接触线、吊弦等设备安装完毕后的负载。负载的变化直接影响承力索弛度，弛度的变化最终通过张力变化表现出来，前文1.2节已经得出张力的状态方程，在此不再叙述。

1.6 坠砣高度b值的计算

由于上述所有计算过程均考虑到线索的延伸，因此坠砣高度可由下式确定[2～4]：

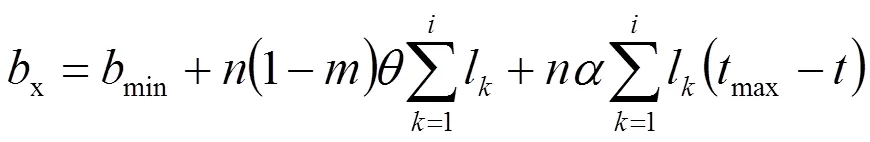
式中，x为坠砣底部至基础面高度，m；min为坠砣底部至基础面最小允许高度，m；为补偿滑轮传动比；k为半个锚段长度，m；max为最高计算温度，℃；为安装时温度，℃。

2 几点讨论

（1）若不考虑新线延伸量，即= 0，则由式（9）可得

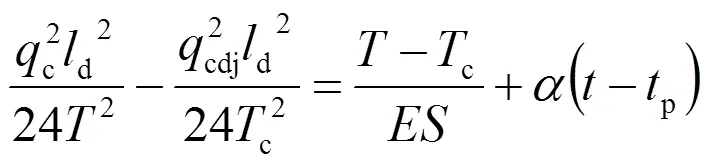
（2）若不考虑新线延伸的影响，架线在平均温度下进行，即(-p) += 0，则由式（9）得

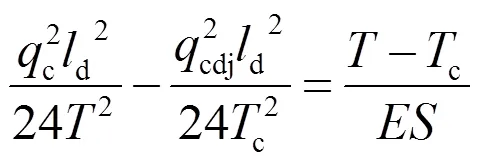
（3）若不考虑新线延伸的影响，架线在平均温度下进行，且忽略线索的弹性伸长，即(-p) ++ (-c) /= 0，则由式（9）得

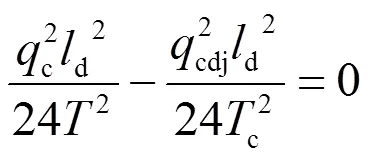
对于上述（1）、（2）2种情况，若架线后即倒线，则应考虑新线延伸对腕臂偏移量的影响。此时腕臂的偏移量应以中心锚结为始算点，向2个下锚方向计算，即

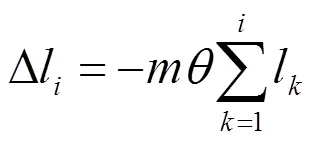
对第（3）种情况，若架线后即倒线，则应综合弹性伸长和新线延伸对腕臂偏移的影响。此时腕臂的偏移量应以中心锚结为始算点，向2个下锚方向逐跨计算，即

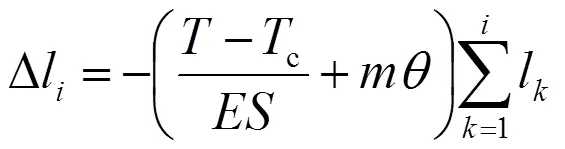
若接触线和承力索同时架设，计算张力变化所产生的影响时，除了得出在承力索架设时对应温度所采用的张力外，还应考虑无自动补偿状态下的弛度和拉伸应力。其状态方程为[5]

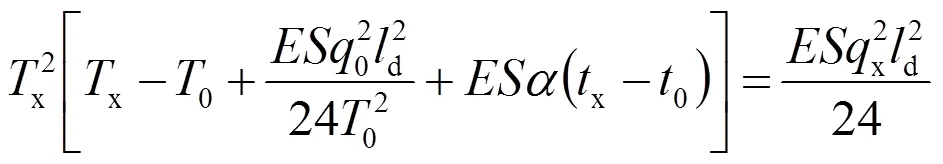
当确定在-10℃的区段，当量跨距为56.547 m，安装温度为20℃，初始张力为8 kN。由上式可计算架线后张力x= 10.946 5 kN，即在-10℃时，张力为10.946 5 kN，温度上升到50℃时，架线后张力降为2.421 kN。-10℃时对应的弛度为0.16 m，而50℃时弛度为0.5 m，两者相差0.34 m。虽然该现象对总锚段长度并无影响，但施工时需提前计算好弛度的变化量，以便控制架线张力（表2），然后得出架线张力与弛度的关系曲线，如图2所示。

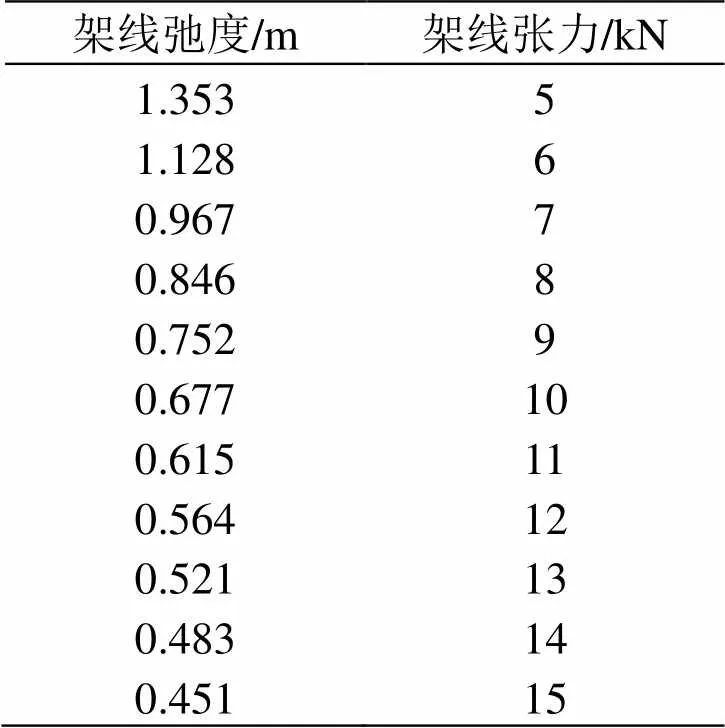
表2 承力索安装表

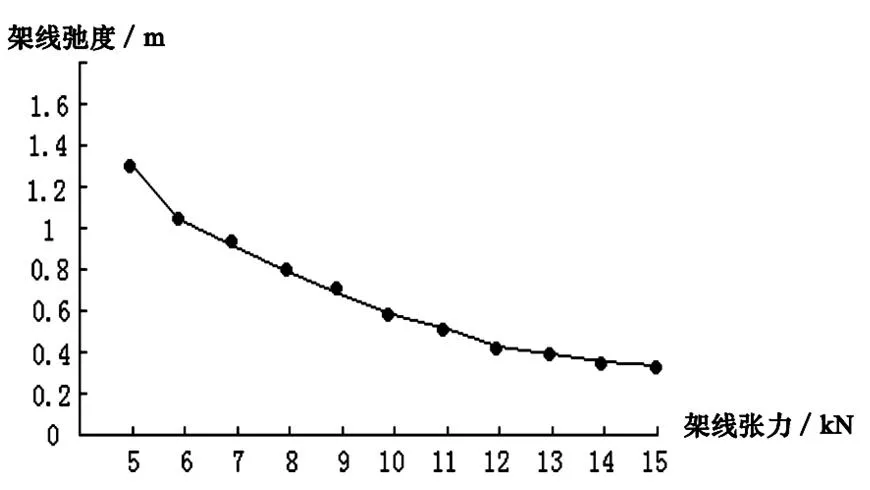
图2 承力索弛度曲线

3 结论

在承力索架设施工中，应先通过=()曲线关系确定放线张力和值，然后按照既有承力索状态安装中锚，最后将承力索倒入承力索座中。倒线前需先确认腕臂是否处于支柱中心位置。如遇到曲线区段，可对腕臂采取防偏移措施。若接触线与承力索同时架设，则需考虑负载与弛度、张力的关系，并确定安装曲线。

根据以上分析，可以得出张力和温度是影响恒张力架设承力索的2个最关键因素，通过确定张力、温度二者的状态关系曲线，找到其规律性。该方法在遂渝铁路接触网施工中得到应用。

4 结语

本文讨论了承力索架设施工时所采用的张力以及坠砣值的确定；在接触网链形悬挂计算的基础上，考虑了新线的初伸长，对接触网链形悬挂计算有一定拓展；计算得出的安装曲线具有更高的准确性和更好的操作性，可直接指导现场施工作业。

[1] 于万聚. 高速电气化铁路接触网[M]. 成都：西南交通大学出版社，2003.

[3] 袁玉森. 接触网承力索架线一次到位施工技术[J].电气化铁道，2005（3）：5-7.

[5] Kießling, Puschmann, Schmieder．电气化铁道接触网[M]．中铁电气化局集团译．北京：中国电力出版社，2004．

With calculation theories for overhead contact line with catenary suspension as the basis, the paper discusses the influencing factors for messenger wires erected with constant force, two types of installation curves are obtained under different conditions, which are better for realizing the wire erection of wires once-at-a-time.

Overhead contact line system; messenger wire; erection; once-at-a-time; application

U225.5

B

10.19587/j.cnki.1007-936x.2018.01.011

1007-936X(2018)01-0047-03

2017-03-01

黄 河.中铁八局集团电务工程公司，高级工程师。