轮辐式马鞍形单层索网结构索长和外联节点坐标组合随机误差影响分析

阮杨捷　 罗　斌　 魏程峰　 郭正兴　 夏　晨　 李金飞

(1东南大学混凝土及预应力混凝土结构教育部重点实验室, 南京 210096)(2中国中铁二院工程集团有限责任公司, 成都 610031)(3上海市政工程设计研究总院(集团)有限公司, 上海 200092)

索杆张力结构由拉索和压杆构成,也可由拉索单独构成,如索桁架、索穹顶、索网等,其施工成型状态受索长和张拉力影响较大．张力结构拉索根数较多,为节省设备投入和提高张拉效率,一般将拉索分为采用张拉设备进行直接张拉施工的主动索和受主动索张拉的影响而被动受拉的被动索2个部分,相应的施工技术称为被动张拉技术,施工控制的关键是主动索的张拉力、被动索的索长以及外联节点的安装坐标．因此,需要在施工前进行被动索长和主动张拉力的误差影响分析,以确定合理的控制指标,同时,在满足施工质量的前提下尽量减小甚至不设索头调节量,以节省材料费用．浙江大学紫金港校区体育馆钢屋盖的桅杆斜拉索网采用了主动同步张拉8根背索后复拉校验4根落地稳定索的张拉方案[1]．文献[2]以该工程为案列,假定索长误差变量服从正态分布,选择不同的主动张拉索系进行误差对比分析,分析结果支持了实际张拉方案的合理性．

一些大型张力结构的施工方法,是将低空组装的索杆系牵引提升至高空与周边结构连接和张拉．无锡科技交流中心索穹顶采用无支架整体提升牵引的安装方法,主动同步张拉最外环的径向索[3]．文献[4]分析了正态分布钢索随机误差对索穹顶体系初始预应力的影响,并根据结果提出了相应的制作要求．深圳宝安体育场轮辐式空间索桁架结构的施工方案[5]也类似,但各索定长,因此最终液压千斤顶施加拉力的直接目的是将不设调节的索头与周边结构连接就位．文献[6]对该结构进行了施工随机误差敏感性研究,其随机误差采用正态分布．

苏州工业园区体育中心体育场挑蓬为轮辐式单层索网结构,其索网由内环索和辐射状布置的径向索组成,整体呈马鞍形曲面,是一种新型张力结构．本文以该工程为案例,通过随机误差影响分析掌握索长误差和周边钢结构安装误差对索力的影响特性,确定合理的误差控制指标,并展开多种对比分析研究．

1　工程概况

苏州工业园区体育中心体育场的轮辐式马鞍形单层索网挑蓬结构,由径向索、环索、外压环和V形柱构成,结构呈1/4对称(见图1)．外压环呈三维空间曲线,长轴为260 m,短轴为230 m,高差为25 m,标高为+27～+52 m．索网由40根辐射状的径向索和1圈内环索构成,因此共有16根等长的环索．为节省拉索材料费用,拉索均采用定长(不设调节量)的全封闭GALFAN镀层钢绞线索[7],热铸锚索头．

图1　轮辐式马鞍形单层索网结构三维图

屋面次结构由二铰钢拱与平衡钢拱水平推力的构造索组成,其上覆盖PTFE膜材．钢柱和受压外环梁主要采用圆钢管截面,部分柱采用圆钢管和方钢管组合截面．

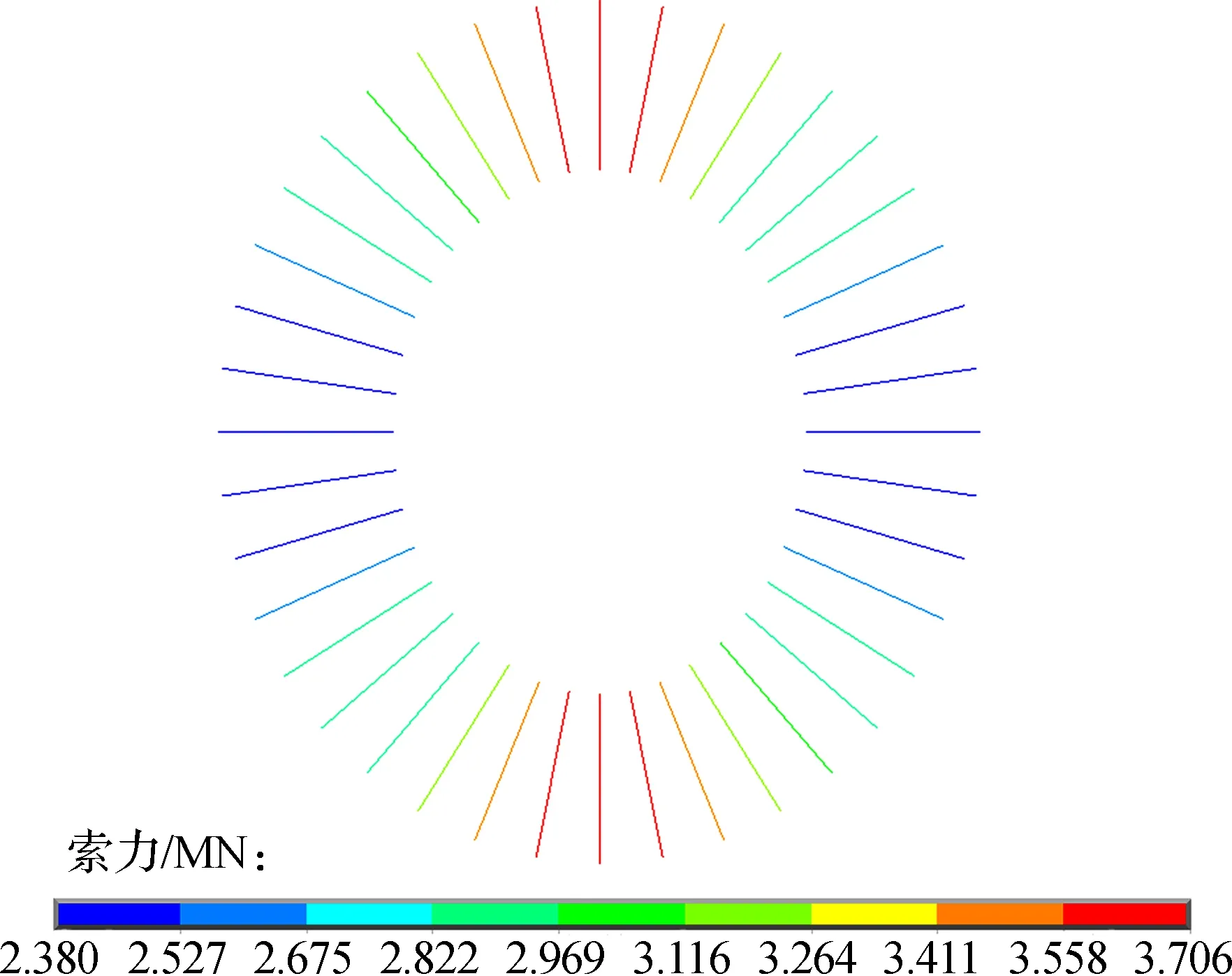
该索网施工采用无支架整体牵引提升、高空分批锚固的方法,包括低空无应力组装、整体牵引提升和高空分批锚固3个阶段[8]．施工步骤如下:① 在设计位置安装外环钢构;② 在近地面和看台上组装索网(包括径向索和环索);③ 提升千斤顶通过挂架与外压环上的临时耳板连接固定,利用工装索斜向牵引径向索的边索头,将索网提升至高空,且提升过程中分批将径向索与外压环连接就位．本文采用ANSYS有限元软件[9]进行计算分析,结构成型时的索力见图2．

2　误差影响分析方法

由于本工程拉索均定长,因此所有拉索均为被动张拉索．根据拉索是否直接与外围结构连接,分为外联索和内联索,则径向索为外联索,内环索为内联索．误差类型主要包括索长误差和外联节点坐标(周边钢结构安装坐标)误差,可表示成如下的矩阵形式:

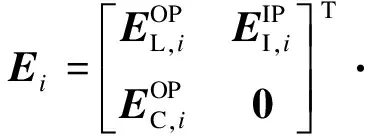
(1)

(a) 径向索

(b) 环索

图2结构成型的索力分布

在进行外联节点坐标误差分析时,可将其等效转换为外联索的长度误差,即附加的外联索索长误差．因此,外联索索长总误差可记为

(2)

式(1)可改写为k+m行向量,即

(3)

表1　拉索长度允许偏差

注：L为拉索长度;|eL|为索长误差绝对值．

2.1　误差分布模型

影响索长制作误差的因素众多,如设备误差、测量误差、温度变化、材料性质变化等．分别假定索长误差服从正态分布、均匀分布和定值分布,进行索长和外联节点坐标随机误差组合分析．其中,正态分布是期望为μ、方差为σ2的连续概率分布．均匀分布是低限为a、上限为b的连续概率分布．定值分布是指索力误差|eFR|≤10%、索长误差绝对值|eL|≤0.01%L的概率分布[11]．

2.2　误差组合

基于正态分布、均布分布和定值分布3种误差分布模型,分别进行索长误差独立分析和索长、外联节点坐标误差组合分析,共设置6种误差组合(见表2)．

表2　误差组合

误差组合分析过程如下:

① 选择合理的误差分布模型,根据误差限值和保证率确定误差分布模型中各参数值．例如,索长误差限值范围为[-20 mm,20 mm],按不小于99.7%的保证率,假定索长误差服从正态分布时,得到误差的期望值和方差分布为

(4)

(5)

式中，Xmin,Xmax,σ99.7分别为正态分布模型中误差的最小限值、最大限值和具有99.7%保证率的标准差．通过计算可得μ=0,方差σ2=44.45．假定索长误差服从均匀分布,则a=-20或b=20．假定索长误差服从定值分布,则a=-20或a=20．

② 每种误差组合随机生成n个误差工况,然后逐一进行非线性有限元工况分析．以误差组合1为例,对40根径向索按正态分布模型各随机生成500个误差工况，统计经向索长误差，结果见图3和图4．其中,1轴径向索索长误差最小值为-18.19 mm,最大值为18.28 mm,均值为0.03 mm,方差为46.91 mm．误差组合1下某工况中的40根径向索长误差最小值为-18.32 mm,最大值为18.85 mm,均值为0.28 mm,方差为48.35 mm．这些均符合正态分布．

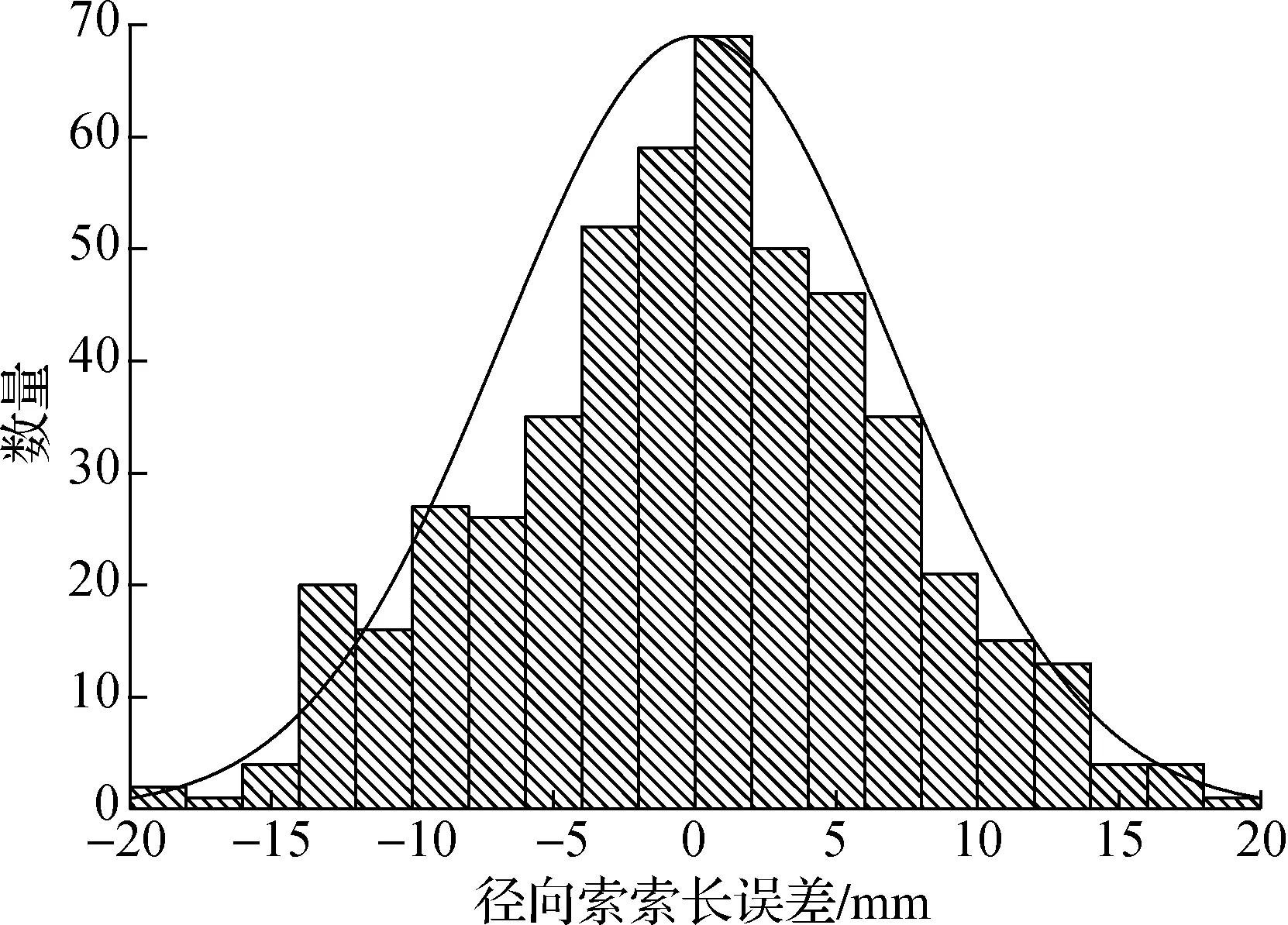
图3　误差组合1下1轴径向索索长误差分布

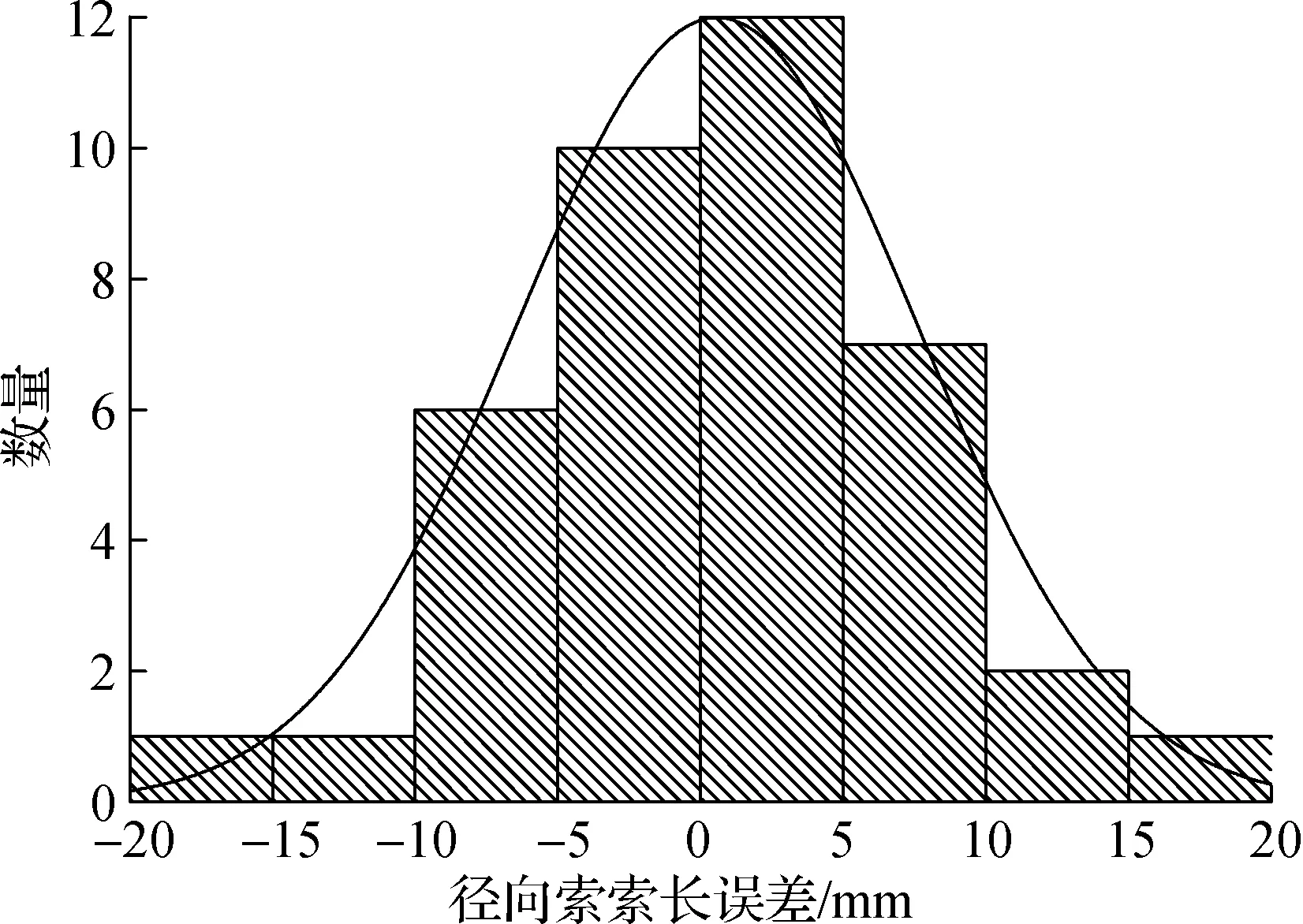
图4　误差组合1下某工况下40根径向索长误差分布

③ 选择合理误差分布模型和保证率,统计n个误差工况与无误差工况的索力误差为

(6)

式中,fi,j,eF,i,j,eFR,i,j分别为第i个误差工况下第j根拉索的索力、索力误差和索力误差;f0,j为第j根拉索的无误差索力．

以误差组合1和误差组合2为例,对各500个误差工况逐一进行非线性有限元分析,统计索单元索力误差,结果见图5和图6．误差组合1中某索单元索力误差的最小值为-4.29%,最大值为4.07%,均值为-0.09%,方差为0.018%．误差组合2中某索单元索力误差的最小值为-5.95%,最大值为5.93%,均值为-0.17%,方差为0.055%．可见,索长误差服从正态分布和均匀分布时,索力误差均服从正态分布．

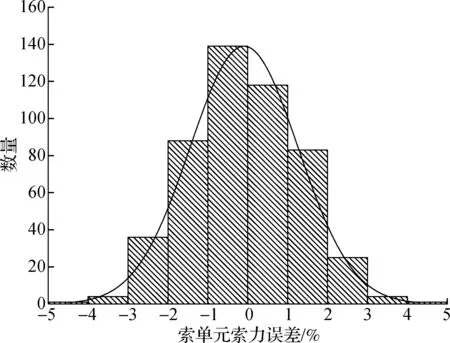
图5　误差组合1中某索单元索力误差分布

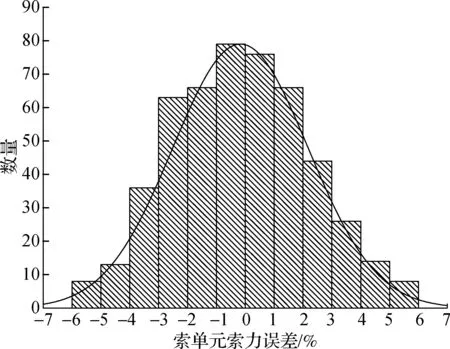
图6　误差组合2中某索单元索力误差分布

本工程采用定长索,结构张拉成型后难以再调整索力．根据正态分布假定,按不小于99.7%的保证率得到索力误差极值,即

eFR,max=μFR+3σFR

(7)

eFR,max=μFR-3σFR

(8)

eFR,abs=max(|eFR,min|,|eFR,max|)

(9)

式中,eFR,max，eFR,min，eFR,abs分别为最大索力误差、最小索力误差和绝对索力误差;μFR,σFR分别为索力误差的均值和标准差．

3　结果与分析

3.1　索长误差影响分析

为了比较不同分布模型下索长误差对结构索力的影响,选定正态分布、均匀分布和定值分布3种分布模型进行对比,即对比误差组合1,2,3的分析结果．由表3和图7可知,不同索长误差分布模型对索力误差的影响差别较大,影响程度从大到小依次为定值分布、均匀分布、正态分布．后续分析中均采用正态分布．

表3　不同分布模型下索长误差对比　%

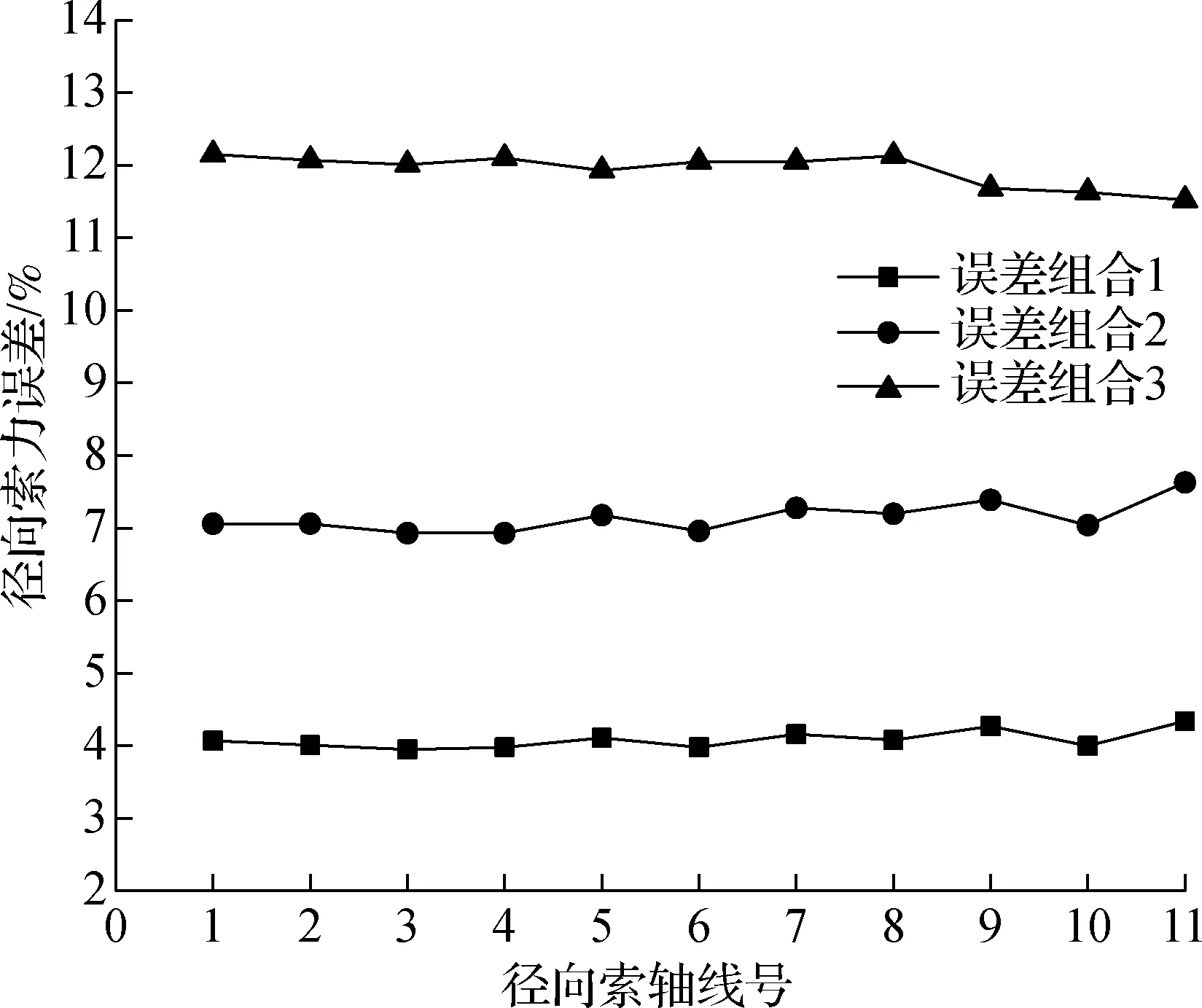
图7误差组合1，2，3的径向索力绝对误差

3.2　径向索和环索索长误差影响分析

为比较径向索和环索索长误差对结构索力的影响程度,将误差组合4和5的结果进行分析对比．由表4和图8可知,环索力受径向索长误差影响较小,径向索和环索的索力受环索索长误差影响基本一致．

表4　径向索和环索索长误差对结构索力影响对比　%

图8误差组合4，5的径向索力绝对误差

3.3　组合随机误差下索长和外联节点坐标的影响分析

为指导周边钢结构安装施工,确定周边钢结构安装坐标误差控制标准,应进行索长和外联节点坐标随机误差组合分析,即对误差组合6进行分析．

为对比不同索长误差控制标准对外联节点坐标允许误差的影响,索长误差限值参考表1中的索长允许偏差值和±0.01%L(径向索L约为±5.2 mm,环索L约为±10.3 mm)进行对比分析,结果见表5．由表可知,从低点的1轴到高点的11轴,外联节点坐标允许误差逐渐缩小．相比表1中索长允许误差,当|eL|≤0.01%L时,外联节点坐标允许误差增大了15 mm,约等于两者索长误差限值的差值,即更严格的索长控制标准可相应放宽外联节点坐标允许误差．考虑到计算模型中的刚度和荷载条件等误差,外联节点坐标误差控制值在理论值基础上考虑1.2倍的安全系数．

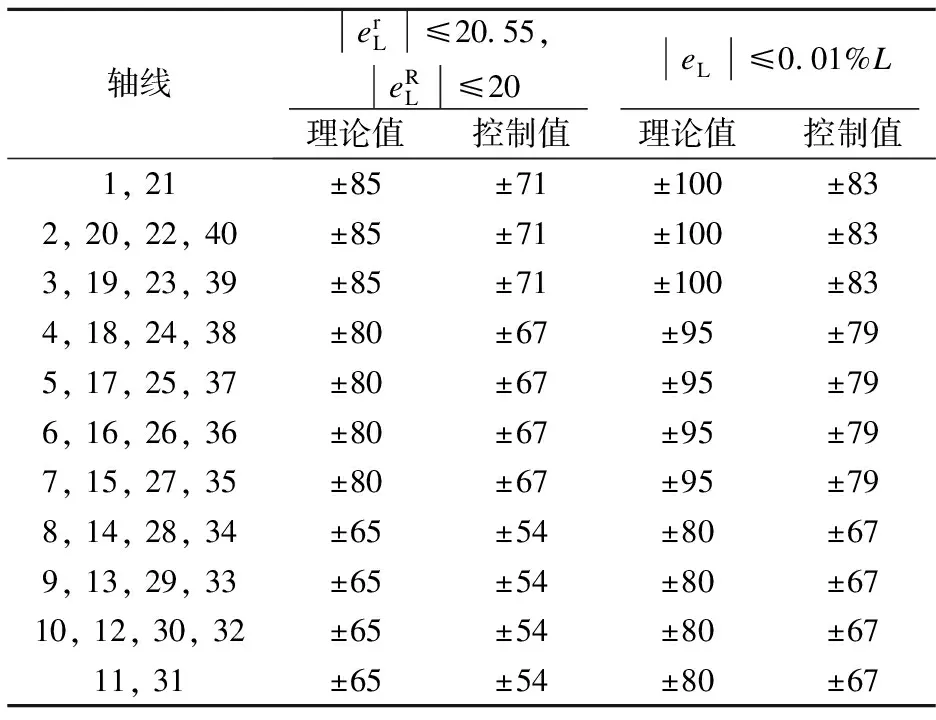
表5　不同条件下外联节点坐标误差限值　mm

假定索长和外联节点坐标误差都符合正态分布,在误差组合1的基础上,逐级(每级5 mm)增大各榀外联节点坐标误差限值eC,直至各榀径向索力误差都临近限值eFR．根据《预应力钢结构技术规程》[12]规定,将eFR取为±10%．误差限值下的径向索力误差见图9．

图9　误差限值下的径向索力误差

根据上述分析结果,综合考虑拉索制作和钢结构安装的工程经验,采用定长索,拉索制作长度误差|eL|≤0.01%L,低处和高处外联节点沿径向索方向的坐标误差应分别不超出±83和±67 mm,即沿径向索方向的外联节点坐标允许误差|eC|≤(67～83)mm,便能满足结构成型时索力误差|eFR|≤10%的要求．

4　结论

1) 不同索长误差分布模型对索力误差的影响差别较大,影响程度从大到小依次为定值分布、均匀分布、正态分布．环索力受径向索长误差影响较小,而径向索和环索的索力受环索索长误差影响基本一致．

2) 将外联节点坐标误差等效为附加的外联索长误差,进行索长和外联节点坐标组合随机误差分析．基于一定的索长误差限值,逐级增加外联节点坐标误差,直至各榀径向索力误差基本达到限值,最终得到外联节点坐标允许误差．

3) 更严格的索长控制标准可相应增大外联节点坐标允许误差,增大值为索长误差限值的差值．

4) 结合理论结果和工程经验,本工程采用定长索是可行的．满足索力偏差值应控制在±10%以内的控制标准为|eL|≤0.01%L,|eC|≤(67～83)mm．

5) 本工程体型大,拉索长度较长,对于具有大量短索的中、小型工程,应进行多种因素的组合误差影响分析,制定更加严格的控制标准．

参考文献(References)

[1] 罗斌,郭正兴,仇荣根. 浙江大学紫金港校区体育馆钢屋盖桅杆斜拉索网施工技术[J]. 施工技术, 2010,39(8):73-77.

Luo Bin,Guo Zhengxing,Qiu Ronggen. Construction technology of stayed cable net of Zijingang district gymnasium steel roof in Zhejiang University[J].ConstructionTechnology, 2010,39(8):73-77.(in Chinese)

[2] 邓华, 宋荣敏. 面向控制随机索长误差效应的索杆张力结构张拉分析[J]. 建筑结构学报, 2012, 33(5): 71-78.

Deng Hua, Song Rongmin. Pretensioning analysis of cable-strut tensile structures for controlling effect of random cable length errors[J].JournalofBuildingStructures, 2012,33(5): 71-78.(in Chinese)

[3] 罗斌, 郭正兴, 高峰. 索穹顶无支架提升牵引施工技术及全过程分析[J]. 建筑结构学报, 2012, 33(5): 16-22.

Luo Bin, Guo Zhengxing, Gao Feng. Research on non-bracket tow-lifting construction technology and complete process analysis of cable dome[J].JournalofBuildingStructures, 2012,33(5): 16-22.(in Chinese)

[4] 张丽梅, 陈务军, 董石麟. 正态分布钢索误差对索穹顶体系初始预应力的影响[J]. 空间结构, 2008, 14(1): 40-42.

Zhang Limei, Chen Wujun, Dong Shilin. Normal distribution manufacture errors and its effects on the intial pre-stress of the cable dome[J].SpatialStructures, 2008,14(1): 40-42.(in Chinese)

[5] 于滨,梁存之,董越,等. 深圳宝安体育场环形空间索桁屋盖张拉成型关键技术[J]. 建筑结构, 2011,41(4):799-803.

Yu Bin,Liang Cunzhi,Dong Yue,et al. The key technology of shape forming processing of ring space cable-truss roof of Shenzhen Baoan Stadium[J].ConstructionTechnology, 2011,41(4):799-803.(in Chinese)

[6] 郭彦林, 王小安, 田广宇, 等. 车辐式张拉结构施工随机误差敏感性研究[J]. 施工技术, 2009, 38(3): 35-39.

Guo Yanlin, Wang Xiaoan, Tian Guangyu, et al. Sensitivity study of random errors for cable tension structure of baoan stadium[J].ConstructionTechnology, 2009,38(3): 35-39.(in Chinese)

[7] Thiem K J, Bechtold M. Properties of and applications with full locked coil rope assemblies[C]//StructuresCongress2017:BuildingsandSpecialStructures. Denver, Colorado, 2017: 495-502.DOI:10.1061/9780784480410.041.

[8] 夏晨. 轮辐式马鞍形单层索网结构性能分析和设计关键技术研究[D]. 南京:东南大学土木学院, 2016.

[9] Madenci E, Guven I.ThefiniteelementmethodandapplicationsinengineeringusingANSYS[M]. Berlin, German: Springer, 2015:47-54.

[10] 中华人民共和国住房和城乡建设部. JGJ 257—2012 索结构技术规程[S]. 北京:中国建筑工业出版社, 2012.

[11] Peacock B, Hastings N, Evans M, et al.Statisticaldistributions[M]. Hoboken, New Jersey, USA: Wiley, 2013: 23-25.

[12] 中国钢结构协会专家委员会. CECS212: 2006 预应力钢结构技术规程[S]. 北京:中国计划出版社, 2006.