基于梯度幅度和梯度方向直方图的全参考图像质量评价算法

王同罕　 贾惠珍　 舒华忠

(1东华理工大学江西省放射性地学大数据技术工程实验室， 南昌 330013)(2东南大学影像科学与技术实验室， 南京 210096)

图像质量评价主要分为主观评价和客观评价.主观评价是由人眼直接观察并进行评价的，符合人的感知特性，结果准确可靠，但容易受客观条件和主观情绪等因素影响，存在评价结果不够稳定、耗时、费用高、难以操作等缺点.根据对原始信息的依赖程度，客观评价可以分为全参考、部分参考和无参考图像质量评价[1].全参考图像质量评价是在参考图像完全可用的情况下评价图像质量，部分参考图像质量是利用参考图像的部分信息对失真图像进行评价，无参考图像质量评价是不需要参考图像的任何信息，直接对图像进行评价.全参考评价算法的结果相对可靠稳定，被称为最可靠的评价算法.

早期的全参考质量评价算法(如MSE和PSNR)没有考虑人类的视觉特性，评价结果与人的主观一致性较差.随后，学者们从人类视觉系统的仿生学角度和基于系统理论的工程学角度来设计评价模型[2-15].其中的典型算法包括SSIM算法[2]、IFC算法[5]、VIF算法[6]、MAD算法[7]、FSIM算法、VSI算法、 GSM算法[10]、GMSD算法[11]等.这些基于工程学的典型算法均采用与人类视觉特性相关的感知特征和有效的池化策略.人类视觉系统理解一幅图像主要是基于其底层特征，如边界和零交叉[11].梯度是边界的构成要素，广泛应用于参考图像质量评价中，如FSIM，GSM和GMSD等.梯度方向直方图可表示边界的结构信息，能准确地描述边界的局部形状信息.基于此，本文提出了一种结合梯度幅度和梯度方向直方图的全参考图像质量评价算法.

1　梯度方向直方图

梯度方向直方图(HOG)的基本思想是，根据一幅图像中的局部强度梯度或边界方向分布，可以准确地描述局部物体表象和形状[16].针对图像I，其梯度方向直方图的提取步骤如下：

Gh(x,y)=I(x+1,y)-I(x-1,y)

(1)

Gv(x,y)=I(x,y+1)-I(x-1,y)

(2)

梯度幅度M(x,y)和梯度方向θ(x,y)分别为

(3)

(4)

② 空间/方向的划分.先将图像按照空间位置划成一定大小的小块，由若干个小块组成一个大的局域分块.根据每个小块内的像素，通过加权投票的方式对方向直方图进行投票.将局域分块中所有小块的方向直方图串联起来，形成局域分块的特征描述子.其中，每个小块的形状可为矩形或圆形；方向直方图的方向取值为0°～180°或0°～360°，一般将方向分为9个通道；加权投票方式一般采用高斯加权，或者根据像素梯度幅度及其相关函数进行加权.

2　基于梯度幅度和梯度方向直方图的评价算法

在本文算法中，首先计算参考图像和失真图像的梯度幅度图以及梯度方向直方图；其次，计算参考图像和失真图像的梯度幅度相似度图和梯度方向直方图的相似度向量；然后，统计梯度幅度相似度的标准方差和所有分块的梯度方向直方图相似度的标准方差；最后，将采用加权方式综合形成整幅图像的相似度标准方差作为失真图像的预测分数值.本文算法的工作框架见图1.

图1　本文算法的工作框架图

2.1　梯度幅度相似度图

人类视觉系统理解一幅图像主要根据其底层特征，如边界、零交叉等.梯度是边界的构成要素，梯度幅度能反应细节变化和纹理变化，广泛应用于参考图像质量评价算法设计中，如FSIM，GSM，GMSD，VSI等.其中GSM，GMSD这2种算法均仅通过梯度幅度相似度来设计评价模型，但二者采用的图像预处理、梯度算子和池化算法不同，这2种模型的预测效果均较好，且GSM的预测效果更优.据此，本文采用梯度幅度相似度作为衡量失真图像失真程度的重要依据之一，采用GMSD进行梯度幅度相似度计算.

梯度通常采用线性滤波卷积进行计算，典型滤波器包括Roberts，Sobel，Prewitt，Scharr等.本文算法采用水平方向Prewitt算子hx和垂直方向Prewitt算子hy来计算图像任意像素点i在水平方向上的梯度Gx(i)和垂直方向上的梯度Gy(i)，进而得到该像素点的梯度幅值G(i).其中，hx和hy分别为

(5)

Gx(i)=I(i)⊗hx

(6)

Gy(i)=I(i)⊗hy

(7)

(8)

令参考图像和失真图像的梯度幅度图分别为Gr和Gd，则梯度幅度相似度图的计算公式为

(9)

式中，C为一个正数常量.Q图是基于像素方式进行计算的，而梯度幅度是基于小局域分块的方式进行计算.Gr(i)和Gd(i)相同时，Q(i)达到最大值1.

2.2　梯度方向直方图相似度

人们识别物体和场景的关键依据是物体和区域的形状.形状作为物体的固有属性之一，主要由封闭的轮廓曲线包围而成，不受颜色、纹理、光照等变化影响，并易于被人眼捕捉，因此形状的失真易于被人眼所观察.梯度方向直方图能很好地描述物体的表象和形状，因此将梯度直方图的相似度作为衡量图像失真的另一个重要依据.其计算过程如下：

① 先按照公式分别计算参考图像和失真图像的水平梯度、垂直梯度、梯度幅度和梯度方向.

② 将参考图像和失真图划块，其中每个细胞大小为8×8.由2×2个细胞组成一个大的局域分块，计算每个细胞的梯度方向直方图.然后，将局域分块中所有细胞的梯度方向直方图串起来，得到梯度方向直方图特征向量.最后，将所有具有一定重叠程度的分块的特征向量组合在一起，形成整幅图像的梯度方向直方图特征.令参考图像和失真图像的梯度方向直方图分别为Xr和Xd. 其中，每个细胞梯度方向直方图的计算方法是假定梯度方向取值范围0°～180°，将其分成9份，然后采用加权梯度幅值的投票方式对梯度方向直方图进行投票.

③ 梯度方向直方图的相似度主要通过方向直方图的均值和方差来衡量，即

T(i)=c(i)k(i)

(10)

(11)

(12)

式中，mr(i)和md(i)分别为参考图像和失真图像中第i个局域分块梯度方向直方图的均值；sr(i)和sd(i)分别为参考图像和失真图像中第i个局域分块梯度方向直方图的方差；T(i)为失真图像的梯度方向直方图的相似度.当参考图像和失真图像中第i个分块相同时，T(i)达到最大值1.

2.3　标准方差加权合并策略

合并策略的选取对于全参考图像质量评价来说至关重要.平均合并策略和加权平均合并策略广泛应用于模型设计中.就预测精度而言，加权平均策略较平均合并策略具有更好的效果，但其复杂度较高. GMSD中，基于单一特征计算相似图时，采用标准方差策略效果较好；基于多个特征计算相似图时，采用标准方差策略的效果较差，究其原因在于不同特征之间的某种关联会导致评价图像质量时更加复杂.基于此，本文采用标准方差加权合并策略，先分别计算梯度幅度相似度图和梯度方向直方图相似度的标准方差，然后通过加权求和的方式得到最后的分数s，即

s=w1D(Q)+w2D(T)

(13)

式中，w1和w2为权重，且w1+w2=1；D为标准方差函数.

3　实验结果与分析

3.1　图像库和评价标准

采取3个公开的自然图像数据库(LIVE[17],TID2008[18]和IVC[19])来验证本文算法的有效性.其中，LIVE库是由美国德州大学奥斯汀分校提供，包含29幅高分辨率的彩色图像以及对应的5种失真类型，每种失真类型又包含几种不同失真程度的图像.该图像库包含982幅图像，其中失真图像779幅.每幅图像都有对应的差分主观分数(DMOS)，其值越大，则图像质量越差.TID2008库是由芬兰坦佩雷理工大学提供.该库由25幅参考图像生成1 700幅失真图像，共包含17种失真类型，每种失真类型包含100幅图像. 25幅参考图像中前24幅为自然图像，最后1幅为失真图像.IVC库包含10幅原始图像和185幅失真彩色图像，共包含4种失真类型.

分析客观评价方法与主观评价相关程度的常用统计指标包括斯皮尔曼秩相关系数(SROCC)、肯德尔秩相关系数(KROCC)、皮尔森相关系数(PLCC)和均方根误差(RMSE).其中，前2种评价指标表征算法预测的单调性，PLCC表征算法预测的精度，RMSE表征算法预测的误差.SROCC，KROCC，PLCC指标越大，说明算法评价准确率性能越高，RMSE指标越低，即评价准确率越高.采用PLCC和RMSE两种指标进行评价前，通常需要进行非线性回归，将预测值和主观分数映射到同一级别，采用的非线性回归方程为[20]

(14)

式中，p(x)为非线性回归后的预测分数；αi(i=1,2,3,4,5)为待拟合的参数；x为原预测分数.

3.2　加权权重设置实验

在标准方差加权合并策略中，需要对算法中的权重进行设置.为了选择合适权重，对3个数据库中不同权重下的SROCC进行了对比，结果见图2.由图可知，在LIVE库上，当梯度幅度相似度图标准差的权重设置为0.3，而梯度直方图相似度标准差的权重设置为0.7时，SROCC值最高；在TID2008库上，当梯度幅度相似度图标准差的权重设置为0.3和0.4时，SROCC值最高；在IVC库上，当梯度幅度相似度图标准差权重设置为0.2时，SROCC值最高.本文算法设置梯度幅度相似度图标准差的权重w1=0.3，梯度方向直方图相似度标准方差权重w2=0.7.

3.3　性能比较实验

在实验中，设置C=170，C1=C2=1.计算梯度幅度相似度之前，需对图像进行2×2高斯加权平均滤波，然后进行下采样.为验证所提算法的有效性，将其与目前具有代表性的8种参考图像质量评价算法(SSIM，IW-SSIM，VIF，MAD，FSIM，GSM，GMSD，VSI)进行比较.这些算法中除了FSIM和VSI能够同时评价彩色图像和灰度图像外，其他算法都是针对灰度图像进行设计的.所提算法与8种代表性算法在LIVE，TID2008和IVC库上的结果见表1.根据3个库中测试图像的个数对各指标进行加权平均，以反映评价算法的总体评价性能.

(a) LIVE库

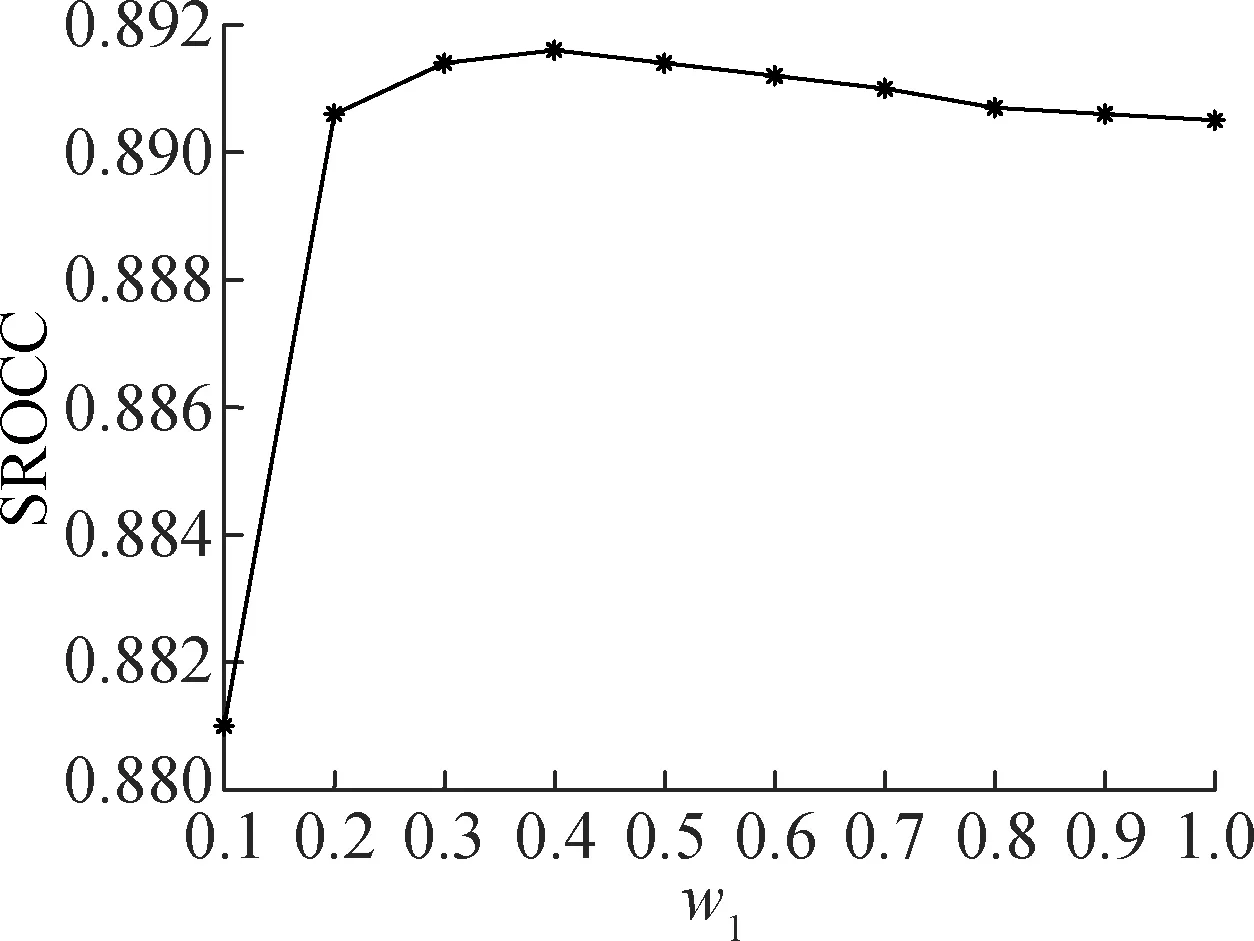
(b) TID2008库

(c) IVC库

由表1可以看出，所提算法的性能均优于主流算法.为了更好地显示各算法预测结果与主观评价的一致性，给出了各算法在TID2008图像库上的散点图，结果见图3.由图可知，本文算法的散点相对比较集中，说明具有较好的主客观一致性.

4　结论

1) 根据人类视觉系统视觉特性，人眼不仅易于捕捉图像细节纹理的变化，并且对局域物体的形状失真比较敏感.梯度幅度可反映纹理细节变化，梯度方向直方图能描述局部物体的表象和形状.基于此，本文提出一种基于梯度幅度和梯度方向直方图的全参考图像质量评价算法.

表1　各算法性能比较

(a) SSIM

(b) IWSSIM

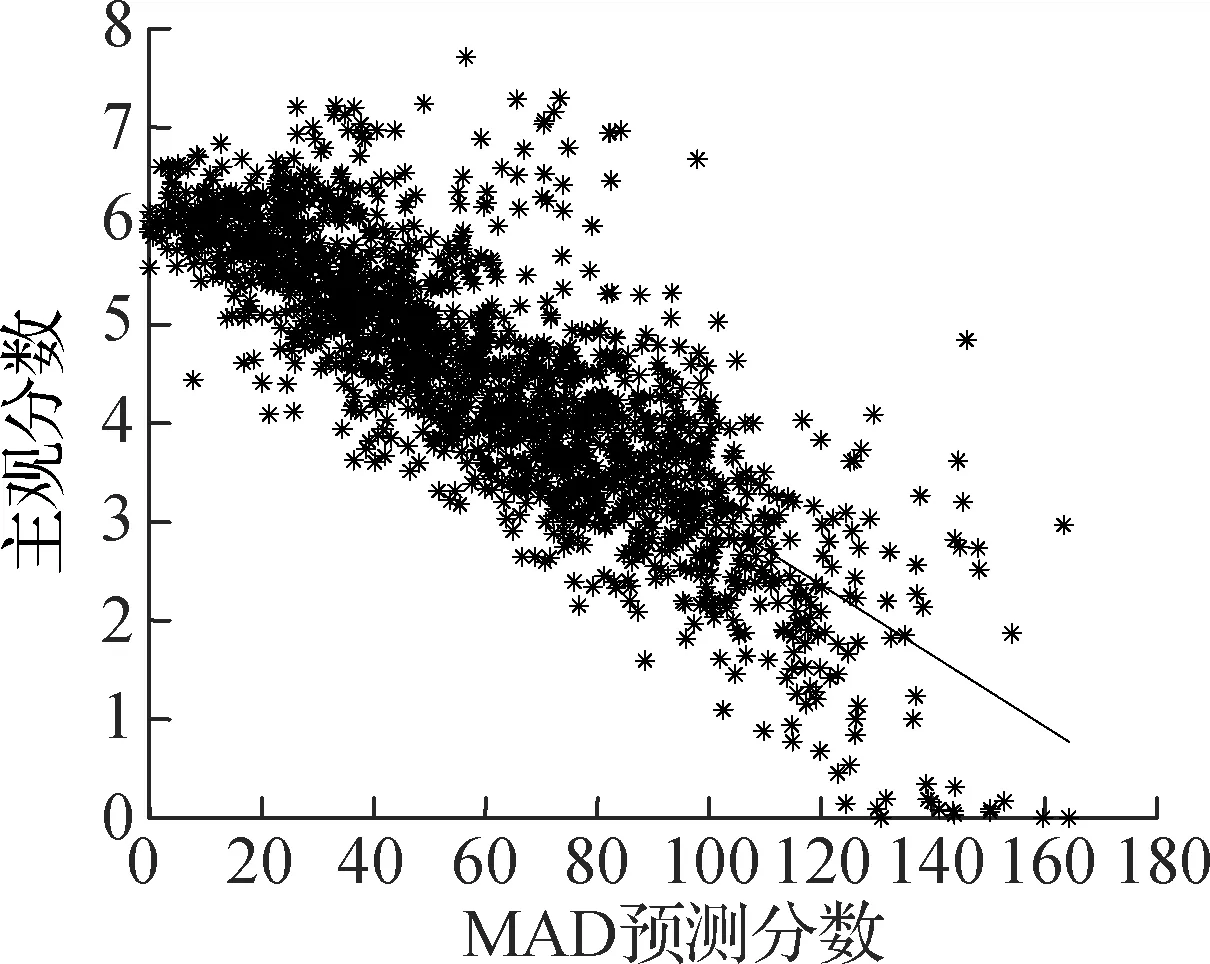
(c) MAD

(d) FSIM

(e) GMSD

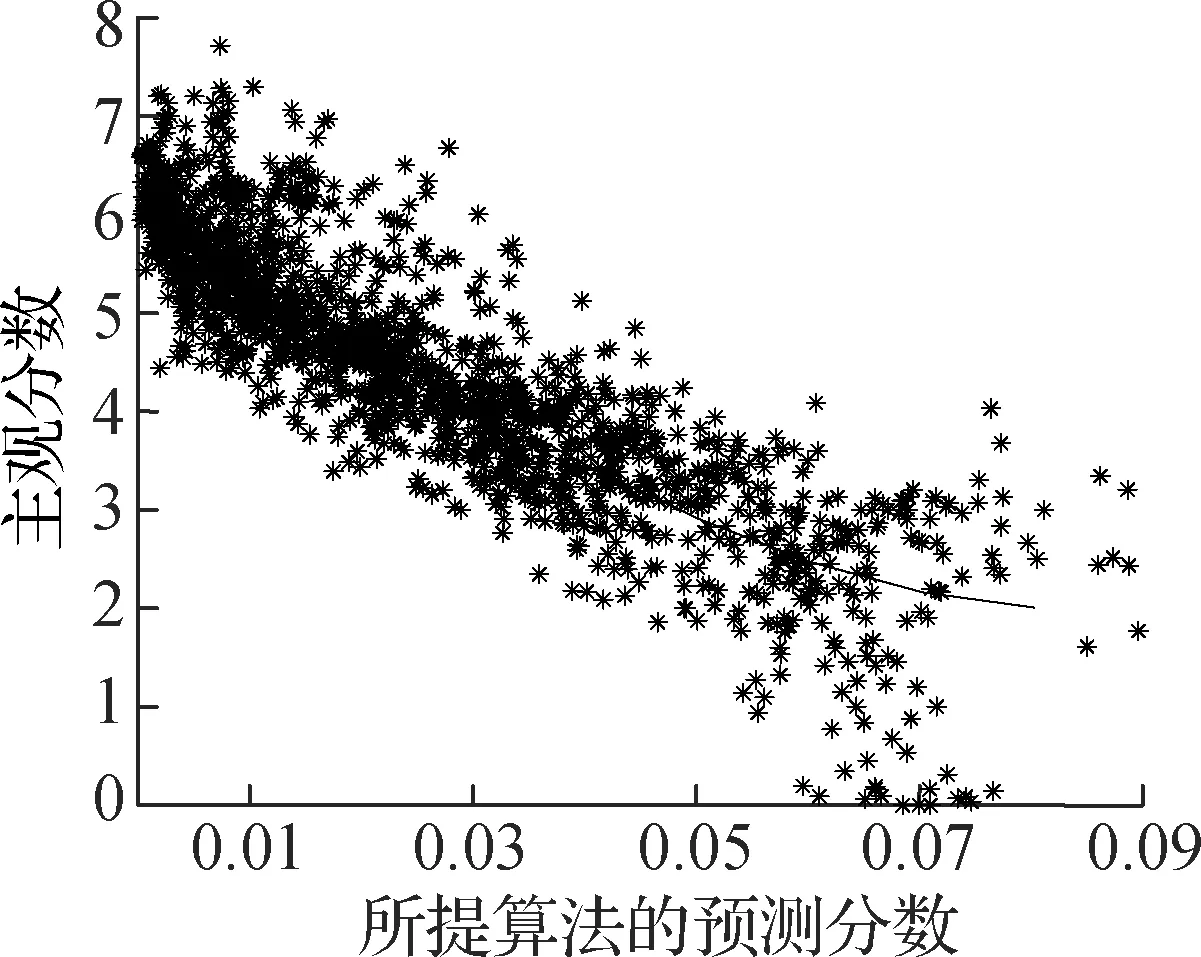
(f) 本文算法

图3各算法在TID2008库上的散点图

2) 在本文算法中，首先提取参考图像和失真图像的梯度幅度特征和梯度方向直方图特征；然后，计算参考图像和失真图像的梯度幅度相似度图和梯度方向直方图相似度向量；最后，采用标准方差加权策略得到失真图像的最终预测值.

3) 3个图像数据库LIVE，TID2008，IVC上的实验结果表明，本文所提算法具有较高的主客观一致性.

4) 下一步工作主要研究梯度直方图分块及细胞大小对图像质量评价的影响，以进一步提高算法的预测性能.

参考文献(References)

[1] Wang Z, Bovik A. Modern image quality assessment[J].SynthesisLecturesonImageVideo&MultimediaProcessing, 2006,2(1):1-156.

[2] Wang Z, Bovik A C, Sheikh H R, et al. Image quality assessment: From error visibility to structural similarity[J].IEEETransImageProcess, 2004,13(4): 600-612. DOI:10.1109/tip.2003.819861.

[3] Wang Z, Simoncelli E P, Bovik A C. Multiscale structural similarity for image quality assessment[C]//TheThirty-SeventhAsilomarConferenceonSignals,SystemsandComputers. Pacific Grove, CA, USA, 2003: 1398-1402. DOI:10.1109/acssc.2003.1292216.

[4] Wang Z, Li Q. Information content weighting for perceptual image quality assessment[J].IEEETransImageProcess, 2011,20(5): 1185-1198. DOI:10.1109/TIP.2010.2092435.

[5] Sheikh H R, Bovik A C, de Veciana G. An information fidelity criterion for image quality assessment using natural scene statistics[J].IEEETransImageProcess, 2005,14(12): 2117-2128. DOI:10.1109/tip.2005.859389.

[6] Sheikh H R, Bovik A C. Image information and visual quality[J].IEEETransImageProcess, 2006,15(2): 430-444. DOI:10.1109/tip.2005.859378.

[7] Chandler D M. Most apparent distortion:Full-reference image quality assessment and the role of strategy[J].JournalofElectronicImaging, 2010,19(1): 011006-1-011006-21. DOI:10.1117/1.3267105.

[8] Zhang L, Zhang L, Mou X, et al. FSIM: A feature similarity index for image quality assessment[J].IEEETransImageProcess, 2011,20(8): 2378-2386. DOI:10.1109/TIP.2011.2109730.

[9] Zhang L, Shen Y, Li H. VSI:A visual saliency-induced index for perceptual image quality assessment[J].IEEETransImageProcess, 2014,23(10): 4270-4281. DOI:10.1109/TIP.2014.2346028.

[10] Liu A, Lin W, Narwaria M. Image quality assessment based on gradient similarity[J].IEEETransImageProcess, 2012,21(4): 1500-1512. DOI:10.1109/TIP.2011.2175935.

[11] Xue W, Zhang L, Mou X, et al. Gradient magnitude similarity deviation: A highly efficient perceptual image quality index[J].IEEETransImageProcess, 2014,23(2): 684-695. DOI:10.1109/TIP.2013.2293423.

[12] Wang T, Zhang L, Jia H, et al. Multiscale contrast similarity deviation: An effective and efficient index for perceptual image quality assessment[J].SignalProcessing:ImageCommunication, 2016,45: 1-9. DOI:10.1016/j.image.2016.04.005.

[13] Shi Z, Chen K, Pang K, et al. A perceptual image quality index based on global and double-random window similarity[J].DigitalSignalProcessing, 2017,60: 277-286. DOI:10.1016/j.dsp.2016.09.013.

[14] Shi Z, Zhang J, Cao Q, et al. Full-reference image quality assessment based on image segmentation with edge feature[J].SignalProcessing, 2018,145: 99-105. DOI:10.1016/j.sigpro.2017.11.015.

[15] Xing L, Cai L, Zeng H, et al. A multi-scale contrast-based image quality assessment model for multi-exposure image fusion[J].SignalProcessing, 2018,145: 233-240. DOI:10.1016/j.sigpro.2017.12.013.

[16] Dalal N, Triggs B. Histograms of oriented gradients for human detection[C]// 2005IEEEComputerSocietyConferenceonComputerVisionandPatternRecognition(CVPR'05). San Diego, CA, USA, 2005:886-893.DOI:10.1109/cvpr.2005.177.

[17] Sheikh H, Wang Z, Cormack L, et al. LIVE image quality assessment database release 2 [EB/OL]. (2005)[2017-06-02].http: //live. ece. utexas.edu/research/ quality.

[18] Ponomarenko N, Lukin V, Zelensky A, et al. TID2008—A database for evaluation of full-reference visual quality assessment metrics[J].AdvModernRadioelectron, 2004,10(4):30-45.

[19] Ninassi A, le Callet P, Autrusseau F. Pseudo no reference image quality metric using perceptual data hiding[C]//ProceedingsofSPIEHumanVisionandElectronicImaging. San Jose, CA, USA, 2006: 146-157. DOI:10.1117/12.650780.

[20] Sheikh H R, Sabir M F, Bovik A C. A statistical evaluation of recent full reference image quality assessment algorithms[J].IEEETransImageProcess, 2006,15(11): 3440-3451. DOI:10.1109/tip.2006.881959.