抓本质悟思想 提升数学素养

谢秀兰

（长乐区教师进修学校，福建 长乐 350200）

《义务教育数学课程标准（2011年版）》教学建议部分明确提出：“数学思想蕴涵在数学知识形成、发展和应用的过程中，是数学知识和方法在更高层次上的抽象与概括。”由此，数学思想应成为小学数学课堂教学的具体目标而加以落实，这就要求一线教师要研读教材，努力挖掘提炼隐含于教材知识技能中的数学思想，让数学思想显现出来，抓住数学知识和数学思想两条主线，并驾齐驱，促进学生数学素养的提升。如果说数学知识是数学的躯干，那么数学思想就是数学的灵魂，怎样才能引领学生深入到数学的“灵魂深处”呢？笔者结合平时的听课与思考，与大家作个交流。

一、在释疑解惑处，领悟数学思想

著名物理学家李政道博士说：“什么是学问？就是要学怎样问，就是学会思考问题。”［1］问题是数学的心脏，一切思维都是从问题开始的，正如爱因斯坦所言：“提出一个问题往往比解决一个问题更为重要。”因而，教师要注重培养学生的问题意识，鼓励学生大胆质疑问难，让学生在质疑问难中主动思考，积极求知，在思维碰撞中释疑解惑，领悟数学思想方法，学会思考，学会学习。

例如，2017年10月29日，笔者在福州仓山小学有幸聆听了浙江省特级教师顾志能老师执教的四年级数学拓展课《九宫格的秘密》。上课伊始，顾老师播放《射雕英雄传》视频片段，从情境中引入探究问题：用1—9九个数字，放入九个格子中，要求无论横的竖的斜的加起来的和都是15。学生明确题目要求后，自主摆卡片，顾老师展示了三位学生的摆法（如图1、图2、图3），以及《射雕英雄传》中黄蓉的口诀“二四为肩，六八为足，左三右七，载九履一，五居中间”以及郭靖摆的九宫格（如图4），顾老师进一步引导学生观察对比，并通过上下、左右交换和课件旋转沟通不同方法之间的联系。为了让学生明白原理，顾老师说：“你们有什么想问的？”鼓励学生质疑问难，教师选择有价值的问题板书在黑板上：①中间数为什么是5？②横的竖的斜的，加起来的和为什么是15？③共有多少种摆法？④四个角都是双数，单数可以吗？对于第①个问题“中间数为什么是5？”换一种说法就是“中间数用其他数可以吗？”，顾老师让学生用“6”做实验，先尝试摆一摆，并请一个学生上黑板摆，可学生怎么摆都不成，这时顾老师及时引导，不能这么光做实验，要动脑思考，能不能只拿一张卡片就能打败这个问题？一语惊醒梦中人，学生从无序摆进入了有序思考，拿出卡片“9”，边摆边说明理由，不管9放哪格，与6的和是15，再加一个数就超过15了，所以中间摆“6”不行。顾老师紧追着问，中间摆“7”行吗？学生稍作思考：那更不行了，9与7的和都超过15了，由此看来，比5大的数都不行了！顾老师继续引导，那比5小的数行吗？能不能也凭一张卡片就能打败这个问题？学生通过尝试、推理，得出比5小的数都不行。最后，顾老师小结，比5大的不行，比5小的也不行，就只能填“5”了，这过程就叫作推理。

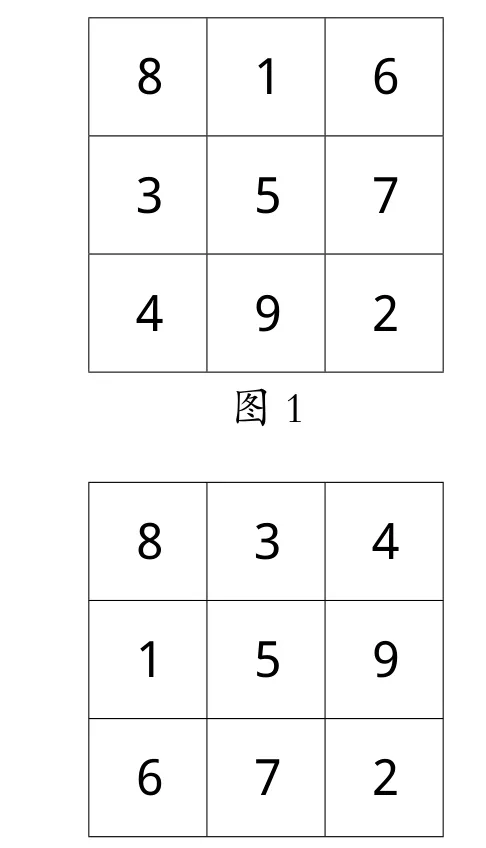
图3

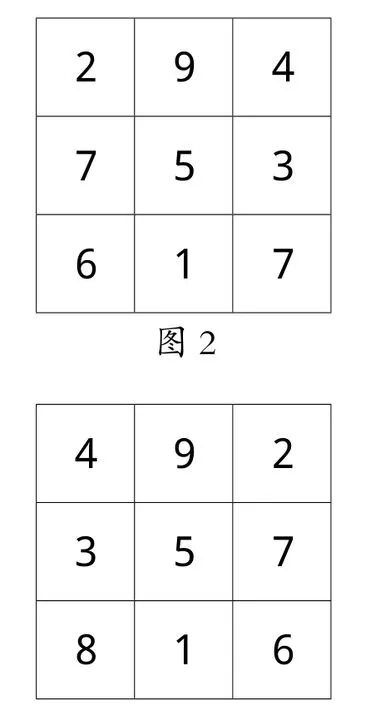
图4

在“五居中间”的探秘过程中，顾老师把1—9九个数字分为“5”与“非5”两类，通过摆“比5大的数”与“比5小的数”都不行，来证明只能摆“5”，让学生体会反证法思想；顾老师先让学生用“6”做实验，从学生无序摆中引导学生思考，能否只拿一张卡片就能打败这个问题，运用了举例验证的方法，让学生体会有序思考的思想；以“6”作为例子，让学生推想“7、8、9”行不行？以“比5大的数”不行，推想“比5小的数”行不行？让学生领悟推理思想的魅力，学生在释疑解惑中学会思考、学会学习，思维能力和数学素养都得到了提升。

二、在亲历过程中，体验数学思想

数学思想方法总是伴随着数学知识发生、发展的过程而显现出来的，因而，教师应想方设法让学生亲历知识的形成过程，在过程中充分感知、体验，加深对知识本质的理解，同时对知识背后蕴含的数学思想方法有更深刻的体验，从而提升学生的数学素养。

例如，人教版二年级上册第六单元“7的乘法口诀”一课，许多教师以为教学乘法口诀只是为了快捷计算，于是，“熟记口诀”和“用口诀计算”便成了课堂教学的核心目标。其实，在看似简单的乘法口诀教学中，却蕴含着十分丰富的数学思想方法，需要教师们努力挖掘。曾听过一位教师是这么设计的：以白雪公主和7个小矮人拼摆七巧板的童话引入，学生在欣赏和数数中明确了每个美丽图案都是由7块板拼成的，接着，教师借助数轴这个直观模型，动态地呈现小矮人在数轴上站队的画面，并且每站上一个小矮人，就在落脚处点上一个点，标上相应的数字或方框（如图5），学生通过观察小矮人站队的全过程，清楚地看出数轴上的点与板块数之间的一一对应关系，“几个7”的表象便清晰地呈现在学生头脑中，为写出乘法算式，理解乘法口诀的来源和含义奠定了基础，学生从中感受到数形结合思想和一一对应思想。当教师编出口诀“一七得七”后，让学生说说这句口诀的含义，然后放手让学生继续编制口诀，并同桌互相说说每一句乘法口诀的含义，即说清每一句乘法口诀是“哪两个数相乘的积是多少”，学生在迁移学习中，真实地经历着口诀的编制过程，加深了对口诀的理解，而口诀的理解又可帮助学生记忆口诀，提高有意记忆能力，同时，充分感受着类比推理思想的魅力。

图5

三、在回顾梳理中，深化数学思想

数学知识具有很强的逻辑性和完整性，而小学数学教材的编排，充分考虑并尊重知识的难易度、小学生的心智特点与思维路径渐进的特点，采取循序渐进、螺旋上升的形式编排。［2］因此，教师在实际教学时，不能只关注一册教材的内容、一个例题的教学目标，而应该对同一个主题的教学内容进行系统梳理，沟通新旧知识间的纵横联系，让学生在感悟数学思想的同时，对某类知识有个系统全面的认识。

例如，2017年10月28日，笔者在福州仓山小学有幸聆听了江苏省特级教师周卫东老师执教的《确定位置》，周老师创设了以“救援故障船”的现实情境引入，扣人心弦，学生如临其境，课堂氛围紧张而热烈，点燃了学生救援的责任和学习的热情，效果非常好。当学生通过大胆猜想、自主探索，明白“方向、角度、距离”是确定位置的三要素后，周老师提出质疑：“三个条件必须缺一不可吗？”接着，他出示信息：1.南偏西，让学生上台在屏幕上圈出可能的区域；再出示信息。2.南偏西25度，让学生上台比划一下可能在哪？最后出示信息。3.12千米，让学生在屏幕上指出来。在这个质疑验证环节中，周老师采用层层递进、步步追问的方式，让学生在比划中加深认识，如果只告诉方向，就只能确定物体可能在哪个“面”上，加上角度后就能确定它在一条“线”上，再告诉距离就能找到这个“点”。很好地沟通了“面、线、点”与“方向、角度、距离”之间一一对应关系，感悟数形结合思想和模型思想，让学生深刻认识到“确定位置”的过程本质即是“由面到线，再到点”，学生的空间观念、思维能力也得到锻炼与提高。在课末，周老师还引领学生回忆确定位置的知识在小学阶段一共接触过几次？然后大屏幕呈现一年级时学习的“上下前后左右、排第几”；四年级学习的“第几排第几个，用数对表示”；今天学习的“用方向、角度、距离确定位置”。从一维到二维，用数对表示到学会用三要素确定位置，学生在回顾梳理中体会新旧知识的联系，在感悟类比思想与模型思想的同时，实现对知识结构的整体把握，学生的数学素养也得以提升。

四、在习题创编中，内化数学思想

习题是例题的延伸和拓展，往往蕴含着丰富的知识、思想和方法，需要教师巧用、活用，把习题中所蕴含的数学思想方法挖掘出来，最大限度地发挥每道习题的功效，让学生在操练中拓宽思路，感悟思想，掌握方法，提升素养。

例如，人教版三年级下册“长方形、正方形面积的计算”一课，福清实小的林老师到长乐实小进行校际交流时，课尾设计的一道练习题给笔者留下深刻印象：“在方格纸中画出面积是12平方厘米的长方形，要求先在头脑中想象是怎样的长方形？然后再画出来。”学生呈现了三种情况：①长12，宽1；②长6，宽2；③长4，宽3。这时，教师利用课件，把长方形从①变成②再变成③，并鼓励学生再想象，长方形的长和宽还可以是怎样的？学生通过课件直观演示与大脑想象，看到了长方形长、宽的变化，而面积不变，函数思想和极限思想深深地烙印在头脑中，学生的思维能力、空间想象能力、数学素养都得到了培养与提升。

又如，人教版二年级上册“乘法的初步认识”，在经历多个加数相同的加法算式可以改写成乘法算式之后，有位教师把练习九第10题进行改造，设计了一组练习：

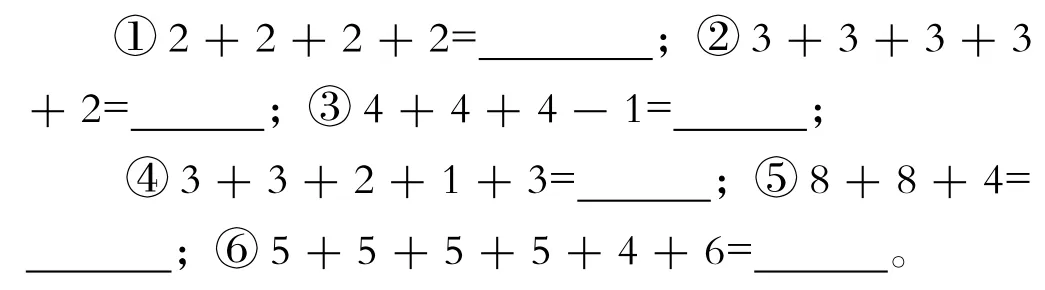
这6道题表面上看，好像只有第①题能改写成乘法算式。于是，教师激发学生思考：哪些算式可以改写成含有乘法的算式？哪些算式通过一些变动也能改写成乘法算式？在教师的启发下，学生把②③写成了乘加、乘减的算式；学生通过观察交流，发现可以把④⑤⑥中的一些数通过合并、拆分、调整等方法来改写。学生从不能改写到能改写，打破思维定势，抓住乘法意义的本质，自觉寻找“加数相同”这个关键，既加深学生对乘法意义的理解，又从中领悟到变中不变的数学思想方法。

史宁中教授说：“数学思想是统领整个数学及数学学习的思想，是数学学科的基石。”［3］教师只有认真研读教材，在触及数学知识本质的同时挖掘数学思想，双线并联共进，才能使课堂教学因显现数学思想而有更高的立意，才能使学生发展成为具有时代气息的有数学眼光和数学思想的人。

［1］席青城．如何培养学生提问意识［EB/OL］．［2017-10-10］． http ：//www．xzbu．com/9/view-5242578．html．

［2］刘延革．宏观视角下分析和把握教材［J］．小学数学教师，2017（5）：76．

［3］史宁中．数学思想概论（第1辑）：数量与数量关系的抽象［M］．长春：东北师范大学出版社，2008．