基于多尺度建模的炼油化工过程报警根源分析

胡瑾秋， 蔡　爽， 张来斌

(中国石油大学 机械与储运工程学院， 北京 102249)

炼油化工生产过程从原料到产品的生产需要经过许多工序和复杂的加工单元，通过多次反应或分离完成。其流程复杂，工艺条件苛刻，常伴有高温、高压、低温、真空、大流量、高转速等极端条件，在炼油厂区，若某单一设备或工艺过程出现故障，极易借助系统单元之间的相互依存、相互制约关系，触发连锁效应，由一种扰动或故障经过一段时间传播，从一个地域空间传播至另一个更广阔的地域空间，引起衍生事故，带来难以估量的社会与环境风险，引发一系列故障链直至引起事故或灾难。为了及时找出故障原因以有效抑制故障传播，保证生产过程安全及产品质量，国内外学者对炼油化工过程报警根源分析方法进行了一系列的研究。

报警泛滥是工业过程报警系统中存在的主要问题之一。对过程变量报警根源进行分析，可及时抑制异常扰动的进一步传播以减少报警泛滥现象的发生。为了辨识炼油化工过程的扰动传播根源，基于过程知识建立过程拓扑模型有助于进一步分析报警根源，如多层流模型(Multilevel flow model，MFM)[1]，因果模型(Cause-effect model，CE)[2]，符号有向图(Signed directed graph，SDG)[3]等。Dahlstrand[1]采用多层流方法表达过程变量间的因果关系。Wan等[2]将CE模型引入到一个逻辑和系统化的报警系统设计方法中。符号有向图是因果图的一种，对过程变量间的因果关系和故障传播路径提供了简单和图形化描述，并且可以在缺乏详细过程知识的条件下根据经验或基本定律来建立符号有向图模型[4-7]。知识建模方法简单实用，易于理解，但严重依赖于过程知识不包括定量信息；此外，模型容易受人的主观判断影响[8]。数据驱动方法如时滞关联分析[9]，信息理论方法(传递熵，直接传递熵)[10-11]，贝叶斯网络模型(Bayesian network，BN)[12]等，也可用于实现报警根源的辨识，以便从根本上抑制滋扰报警和报警泛滥现象的出现。关联性并不一定代表因果性，但如果引入时间延迟，可找出两时间序列间关联系数的最大值，其对应的时间关系可以近似地反映因果关系。互相关函数(Cross-correlation function，CCF)[9]可用于估计两报警序列间的时间延迟，通过两序列间的时滞和关联系数，生成对应的因果矩阵和关联系数矩阵，结合一致性检验和拓扑假设，可以构建因果网络[13]。但互相关函数会产生大量冗余时滞干扰分析结果，有时由该数据驱动方法建立的扰动传播路径可能与实际过程不符。因此有必要结合过程知识检验传播路径的合理性。Bauer等[11]和Gao等[14]采用信息理论计算两变量间的传递熵，从本质上反映了信息传递所带来的因果性。Duan等[10]提出直接传递熵概念来检测两变量间是否有一个直接的物质流或信息流，以提高因果图的准确性。Gao等[15]提出基于解析结构模型的信息融合方法，通过构建连接矩阵和可达矩阵构建因果网络，实现报警根源的辨识。概率符号有向图[16]是一种基于实现最大系统可信度的报警信号挑选方法，该符号有向图的建立使过程变量间的因果关系可视化。数据驱动方法可定量分析过程变量间存在的因果关系，但对于分析变量的挑选依然常常根据主观经验，对于一些复杂的大型系统，常涉及大量监控变量，主观挑选模型变量可能遗漏某些重要原因变量，以致无法推绎出引发报警的扰动根源。

因此笔者采用多尺度建模的方法，通过对炼油化工生产系统的空间尺度进行划分，针对不同的风险过程，分析不同尺度下的过程风险表征指标，建立多尺度下的炼油化工过程报警根源分析模型，并对不同尺度下的模型进行应用对比分析，从而选择合适的尺度进行建模，保证炼油化工过程报警根源分析的准确性。

1　时滞分析方法基本原理

时滞分析方法可分析不同过程变量间的时滞和关联关系，从而推断他们固有的因果关系。

时滞分析方法采用互相关函数[9]计算过程变量间考虑时延性的关联函数值。对于两过程变量xi和xj的离散时间序列数据，定义互相关函数φxi,xj(k)为

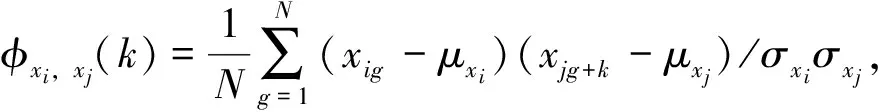
(1)

n为过程变量个数，过程变量xi和xj的时间序列长度为N，其均值为μxi和μxj，标准差为σxi和σxj，xig表示标准化后的变量xi在第g个时刻的变量值，φxi,xj(k)为具有时间意义的k的单值函数。

定义φxi,xj(k)的最大值φmax和最小值φmin为

(2)

记φmax对应的k为kmax，φmin对应的k为kmin，xi、xj间的时滞λi,j表示为

(3)

时滞λi,j用于确定传播方向。若λi,j>0，实际传播方向为xi→xj；反之，传播方向为xj→xi。

两时间序列关联系数ρi,j记为

(4)

因关联系数由统计方法计算得到，每2个时间序列可得一确定值，但若关联系数过小，考虑两变量间的关联性将没有意义。因此有必要设置合适的阈值对关联系数的显著性水平进行检验。笔者采用如下的假设检验方法，通过式(5)计算阈值(ρth(N))[9]，若|ρi,j|<ρth(N)，表明关联系数未通过显著性检验，此时考虑两变量间的关联性将没有意义。ρi,j的正负反映了变量间的关联关系。若ρi,j>0，两变量具有正相关关系，即xi的增加可能引起xj的增加。反之，若ρi,j<0, 两变量具有负相关关系。

ρth(N)=1.85N-0.41+2.37N-0.53

(5)

然而，若φmax和φmin的大小接近，两变量的因果关系将变得模糊，方向性难以确定。为了辨识φmax和φmin的差异性，定义方向性指数(ψ)如式(6)：

(6)

通过式(7)计算方向性指数阈值(σψ(N))[9]，若ψ≥σψ(N)，表明两变量具有显著的因果关系。

σψ(N)=0.46N-0.16

(7)

2　炼油化工过程报警根源分析方法

报警系统作为复杂炼油化工过程的重要组成部分，可有效监控过程的运行状态。报警系统设置是否合理直接影响生产过程的运行。当过程设备异常运行时，将以声光形式触发报警。收到报警后，操作者将结合过程知识调查故障原因并采取必要措施阻止异常的进一步恶化，使设备恢复到正常运行范围。如今，工业过程报警系统的实际问题是报警数过多。实际上，操作者每1 h可能面临数以百计的报警，大量的报警干扰操作者的判断，使他们浪费大量时间处理次要报警而忽视关键报警。因此，需要一个合理的策略进行报警根源分析，及时辨识扰动根源，避免异常风险的进一步发展。

提出一种炼油化工过程报警根源分析方法，通过对炼油化工生产系统的空间尺度进行划分，针对不同的风险过程，分析不同尺度下的过程风险表征指标，从而通过时滞分析并结合过程知识构建扰动传播因果图，最后提出一种报警根源搜索方法辨识最可能的扰动传播路径以找出报警的根本原因。

2.1　炼油化工生产系统的空间尺度划分

炼油厂区包含多套生产装置，如炼油厂主要由炼油过程和辅助设备两大部分组成，经过多个物理及化学的炼油过程将原油炼制成各种石油产品。

炼油生产装置按生产目的可分为原油分离装置、重油轻质化装置、油品改质及油品精制装置、油品调合装置、气体加工装置、制氢装置等。由于生产方案不同，炼油厂中所包含的炼油过程的种类和规模大小各不相同，或者说复杂程度都有所不同。一般来说，规模大的炼油厂其复杂程度更高。此外，辅助设施是维持炼油厂正常运转和生产所必需的，主要的辅助设施有：供电系统、供水系统、供水蒸气系统、原油和产品储运系统、三废处理系统等。这里的研究不考虑辅助设施。

炼油化工生产系统的空间尺度可定义为炼油化工生产系统空间范围的大小。这里的空间范围是指在一定尺度的系统中进行风险分析的范围。根据炼油化工生产系统的规模大小，将空间尺度分为大尺度、中尺度和小尺度3种类型。

其中，大尺度主要包括生产装置级及比其空间范围更大的炼油化工生产系统。其研究区域的范围小至单个生产装置(如常减压装置、催化裂化装置等)，大至整个炼油厂区。

中尺度则主要指单元级。其研究区域的范围为生产装置中的某一单元。

传统分析中，单元的定义为整体中自为一组或自成系统的独立单位。在安全生产风险管理中，为了保证风险辨识的科学性、系统性、合理性和可操作性而将研究对象整体按照某种规则划分为相对独立的部分。因此，这里的单元是指将某个生产装置按照其生产功能划分的各个相对独立的部分。如催化裂化装置可划分为反应再生单元、分馏单元、吸收稳定单元等。

小尺度主要是指设备级，其研究区域的范围为某一过程设备，这里的设备包括各种塔器、反应器、换热器、各类储罐等，如提升管反应器、分馏塔、回炼油罐等。

具体的尺度划分如表1所示。

表1　炼油化工生产系统空间尺度划分Table 1　Spatial scale division of refinery production system

2.2　多尺度风险表征指标辨识

随着炼油化工过程工艺、技术的提高和装置大型化发展，保证过程的安全、平稳、长周期运行成为炼油化工企业日常管理的重点，也是实现炼油企业效益最大化的有效途径。因此，为避免发生各类非计划停车、泄漏、火灾、爆炸等事故，需对炼油化工过程风险及其风险表征指标进行辨识研究，以便准确、及时的对炼油化工过程风险进行状态监测及报警根源诊断，有效抑制异常扰动的进一步传播。

通过统计现场炼油化工过程采集的监控变量数据，可根据某一风险发展过程中一段时间内各变量的报警数量及其扰动变化趋势，辨识不同尺度下与风险发展密切相关的监控变量作为过程风险表征指标。这里的多尺度风险表征指标辨识方法主要包括如下两个步骤：

(1)统计某炼油化工企业近两年事故记录中每次某一风险发展过程前后的一段时间内不同尺度下各监控变量的报警数量，因报警数的多少反映了风险发生时对该变量的影响大小，因此，这里根据专家经验选取多次统计数据的平均报警数多于5个的变量作为待选的风险表征指标。

(2)因受风险影响较大的变量必然会产生明显的扰动，可根据其扰动变化趋势的大小进一步确定过程风险表征指标。这里采用最小二乘线性拟合方法对上述不同尺度下的待选风险表征指标在每次风险发展过程中一段时间内的数据进行拟合，并以所求斜率的平均值作为该变量的扰动变化率，其绝对值的大小可近似反映变量的扰动变化趋势，若扰动变化率的绝对值过小，说明该变量并未产生大的波动，即无法较好的表征风险发展过程。因此若扰动变化率的绝对值小于某一阈值(根据专家经验设置)时，不使用相应的变量作为冲塔风险表征指标。

其中，扰动变化率定义如下：

定义1：对于某一过程变量xi，考虑以时刻κ为中心，选择时间间隔为[κ-m,κ+m] (时间序列长度为2m+1)的变量xi的时间序列进行最小二乘线性拟合如式(8)，所求斜率ai的大小作为变量xi的扰动变化率。

令xig=aitg+bi,g=κ-m,…,κ,…,κ+m,i= 1,…,n，n为过程变量个数，xig为标准化后的变量xi在第g个时刻的变量值，最小二乘线性拟合公式如式(8)：

(8)

对变量xi的标准化公式如式(9)：

(9)

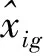
通过上述步骤，即可确定不同尺度下的过程风险表征指标。

2.3　因果图的建立

采用时滞分析方法分析不同过程变量间的时滞和关联关系，可推断他们固有的因果关系，该方法适用于运行相对平稳的化工过程[9]。时滞分析的基本假设是最先引起扰动产生的变量是将风险引入整个过程的根原因。扰动变量不同于异常报警变量。最早出现的报警变量是在故障影响下最先超出预设操作范围的变量，但它不一定是最早的扰动，也不一定是引发报警的根本原因。因此，当报警出现时，有必要通过分析扰动传播路径辨识报警根源从而消除报警。

变量间的时滞信息和因果关系可以通过时滞分析方法来获得，从而构造出两个上三角矩阵。时滞矩阵反映了受扰动影响的两变量间在时间发展上的先后关系。其中元素的正负反映变量间的因果关系。最初受到扰动的变量是后续变量发生扰动的原因。关联系数矩阵中元素的正负反映了变量间的正负相关关系。时滞矩阵L和关联系数矩阵P有下面的形式：

(10)

(11)

两过程变量间时滞λi,j和关联系数记ρi,j分别由式(3)及式(4)求得，并根据式(6)计算两变量的方向性指数ψi,j，根据式(5)计算关联显著性阈值ρth(N)，通过式(7)计算方向性指数阈值σψ(N)，若|ρi,j|<ρth(N)或ψi,j<σψ(N)，ρi,j和λi,j在式(10)和式(11)中将设为0。

基于这些特征，通过时滞分析建立过程扰动传播因果图，如图1所示。因果图由有向弧和代表过程变量xi(i=1,2,…6) 的节点组成。若λi,j>0，有向弧由xi指向xj，即由上级原因变量指向下级结果变量，反之，则传播方向相反。虚线弧表示两变量负相关，即ρi,j<0，实线弧表示两变量正相关，即ρi,j>0。

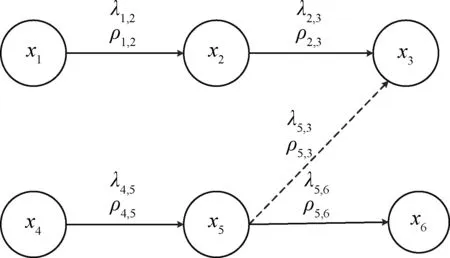
图1　扰动传播因果图Fig.1　Disturbance propagation causality diagramxi(i=1,2,…6) represents the ith process variable node;The dotted line indicates a negative correlation between two variables;The solid line indicates a positive correlation between two variables

但互相关函数会产生大量冗余时滞干扰分析结果。有时由该数据驱动方法建立的扰动传播路径可能与实际过程不符。因此有必要结合过程知识检验传播路径的合理性，对因果图进行修正。

2.4　报警根源搜索方法

当一个报警出现时，报警可能不仅受到相邻变量的影响，也受到传播路径中其他变量的影响。若变量值超出预设控制限，将触发相应报警。但是该报警不一定是最早产生的扰动，也不一定是系统异常的根本原因。在过程中的其它变量受到扰动前发生扰动的变量，受到故障的影响最为直接，故障通过该变量在过程中不断传播进而影响其他变量导致报警的产生。因此找出最初扰动、确定报警的根本原因，操作人员可迅速采取有效措施处理报警。这里提出一种报警根源搜索方法，包括如下4个步骤：

步骤1：相同的报警可能由不同传播路径中产生的扰动引起。为了辨识报警的根本原因，当一个变量xj发生报警时，将其作为下级变量，根据2.3节所提方法建立因果图，据此搜索与该变量直接相连的所有上级变量xi(i=1，2，…，I，I为上级变量个数)，例如，图1中的x3报警，可搜索到其2个上级变量x2和x5。

步骤2：若变量xj在κ时刻发生报警，通过式(8)和式(9)计算xj各相关上级变量xi的扰动变化率ai，其值大小可近似反映下级变量受各相关上级变量扰动的影响大小。

步骤3：比较各相关上级变量的扰动变化率ai的绝对值大小，将ai绝对值最大值对应的上级变量作为其上级原因变量。上级变量的扰动变化率ai的绝对值越大，其对下级变量的影响越大，因此，通过ai绝对值的大小可以比较下级变量受各相关上级变量扰动的影响大小，将ai绝对值的最大值对应的上级变量作为其上级原因变量。若所求扰动变化率的绝对值过小，说明该变量的时间序列数据趋于平稳，并未产生大的扰动传播至下级变量，因此，根据专家经验及历史数据统计，若ai的绝对值小于阈值C，将不考虑该上级变量。

步骤4：重复步骤2和步骤3，将搜索到的最后一个上级变量作为报警的根本原因。这里有必要确定ai所对应的上级变量变化趋势是否与变量间的正负相关关系一致。也就是说，若两变量负相关，一个变量的变化率为正，另一个应该为负；若两变量正相关，一个变量的变化率为正，另一个也应该为正。因此，若对应于ai的上级变量变化趋势与他们之间的正负相关关系一致，扰动可能由该上级变量向下级变量传播；若不一致，根据ai值的大小依次考虑其他上级变量是否满足要求，并重复步骤2和步骤3，将搜索到的最后一个上级变量作为报警的根本原因。

3　炼油化工过程报警根源分析方法步骤

炼油化工过程报警根源分析方法流程图如图2所示，具体方法步骤如下：

步骤1：对炼油化工生产系统的空间尺度进行划分，划分标准见2.1节；

步骤2：采用2.2节所提方法辨识不同尺度下与风险发展密切相关的监控变量作为过程风险表征指标；

步骤3：采用时滞分析方法建立过程风险扰动传播因果图，并结合过程知识检验传播路径的合理性，对因果图进行修正，具体方法见2.3节；

步骤4：当某一过程变量发生报警时，采用所提报警根源搜索方法辨识报警的根本原因，具体方法见2.4节。

图2　炼油化工过程报警根源分析方法流程图Fig.2　Diagram of alarm root cause analysis in refinery process

4　案例分析

催化裂化装置是将重质油转化为轻质油的关键装置，其运行状态不仅关系到整个厂区的安全，同时也决定了产品的收率。由于催化裂化装置是炼油厂最主要和最关键的装置，保持其安全平稳长周期运行是提高催化裂化装置的经济效益、避免各类非计划停车、泄漏、火灾、爆炸等事故的关键所在。从催化裂化装置运行情况来看，随着掺渣比的提高，原料重质化，劣质化，反应再生系统、分馏系统结焦、分馏塔冲塔、催化剂跑损、膨胀节开裂、油浆泵磨损、仪表故障以及人为操作事故等都是导致催化裂化装置无法安全平稳运行的主要因素。分馏单元是催化裂化生产装置的一部分，分馏过程运行相对平稳，是一个非常复杂的物理变化过程。自反应器顶部来的高温油气进入分馏塔人字挡板底部，与人字挡板顶部返回的的循环油浆逆流接触，油气自下而上被冷却洗涤，经分馏后得到的富气、粗汽油、轻循环油、重循环油及油浆。冲塔故障是分馏过程中经常发生的现象之一。当汽液相负荷过大时，气体通过塔板的压降增大，会使降液管中液面高度增加，液相负荷增加时，出口堰上液面高度增加，当液体充满整个降液管时，上下塔板液体连成一片，分馏完全破坏，导致冲塔的发生，严重影响产品质量。造成分馏塔冲塔的原因有很多，如塔盘掀翻或损坏；塔盘有脏物堵塞浮阀或升气孔；有脏物沉淀在塔板上，使溢流堰过低，液层过薄；塔盘结盐；换热器故障，取热不能满足，导致回流温度高引起冲塔；各种机泵故障，如一中回流泵、回炼油泵、顶循泵等故障，机泵故障由带水会不上量(即泵抽空)及各种设备自身问题引起，包括腐蚀、磨损、机封泄漏、入口有杂物损坏叶轮、电机故障等。为了保证产品质量，避免冲塔故障的发生，这里对分馏塔冲塔风险过程报警根源分析进行多尺度建模研究，并对不同尺度下的模型进行应用对比分析，从而选择合适的尺度进行建模以保证过程风险报警根源分析的准确性。

4.1　尺度划分及多尺度冲塔风险表征指标辨识

就分馏塔冲塔风险而言，可主要从分馏塔本身及整个分馏单元两个尺度进行考虑，即设备级小尺度和单元级中尺度两个尺度。

分馏单元本身属中尺度研究范围，其研究区域为催化裂化生产装置中的分馏单元如图3所示，主要包括分馏塔、分馏塔顶油气分离器、回炼油罐、原料油缓冲罐、轻柴油汽提塔及油浆外甩器。对分馏单元的冲塔风险表征指标进行辨识，某石油化工企业催化裂化分馏单元的主要监控变量如表2所示。

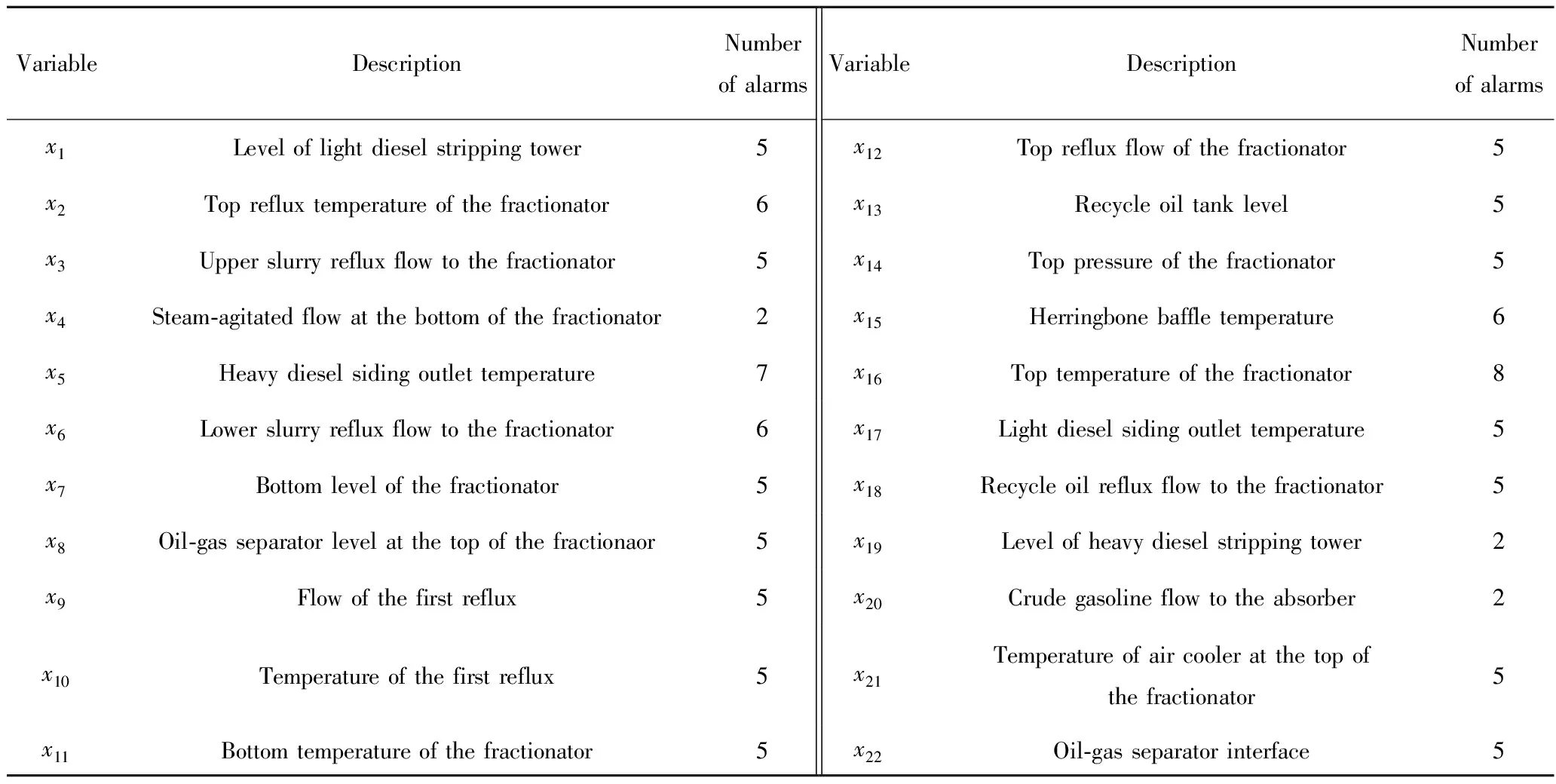
表2　分馏单元主要监控变量Table 2　Main monitoring variables of fractional distillation unit

通过统计某石油化工企业现场催化裂化过程采集的监控变量数据(采样间隔为5 s)，可根据分馏塔冲塔风险发展过程中一段时间内各变量的报警数量及其扰动变化趋势，辨识不同尺度下与风险发展密切相关的监控变量，作为过程风险表征指标。

统计该企业近2年事故记录中每次分馏塔风险发展过程前、后的10 min内不同尺度下各监控变量的报警数量，如表3所示，因报警数的多少反映了风险发生时对该变量的影响大小，因此，这里根据专家经验选取多次统计数据的平均报警数多于5个的变量作为待选的风险表征指标，如表3所示。

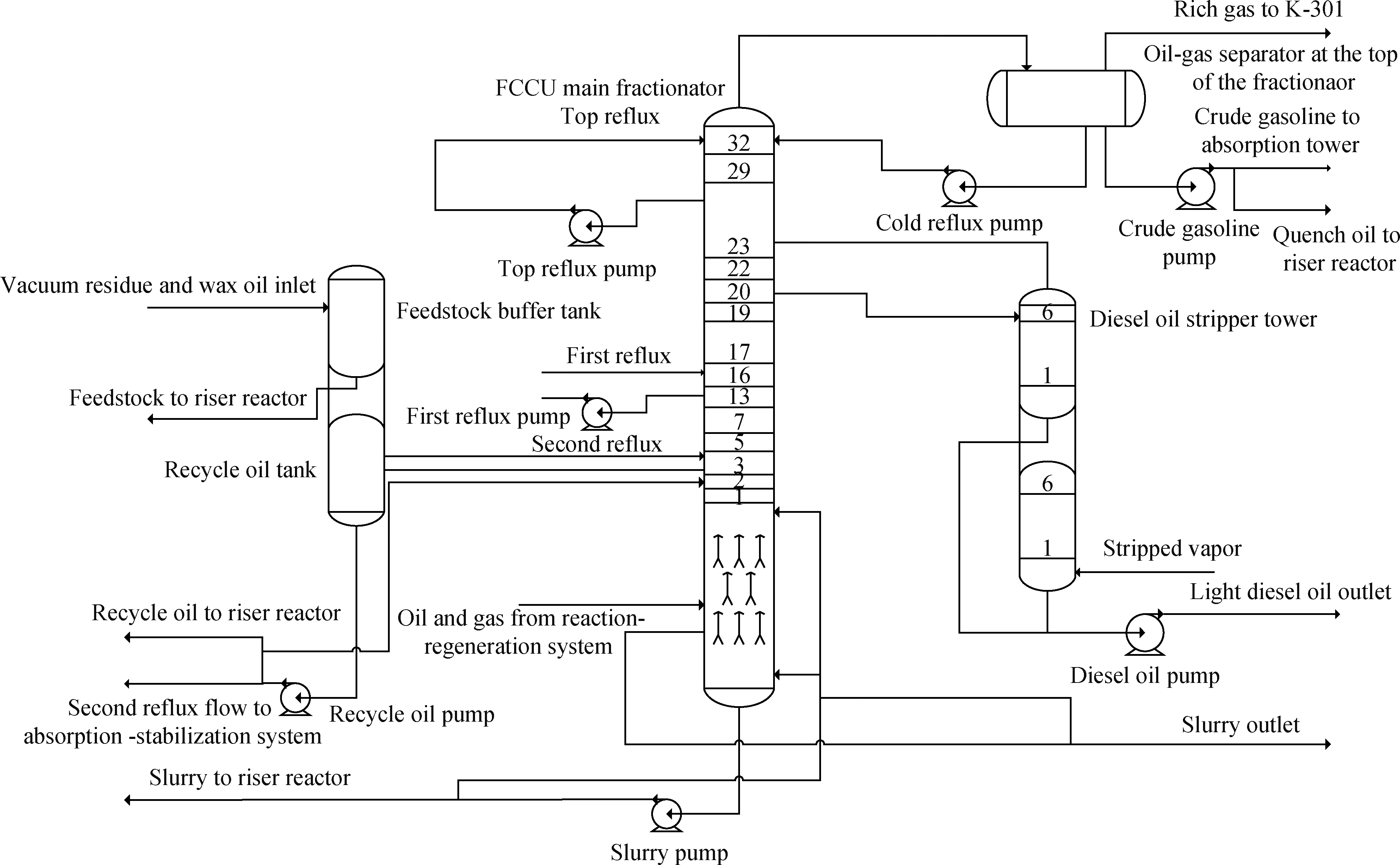
图3　催化裂化分馏单元Fig.3　Fractional distillation unit

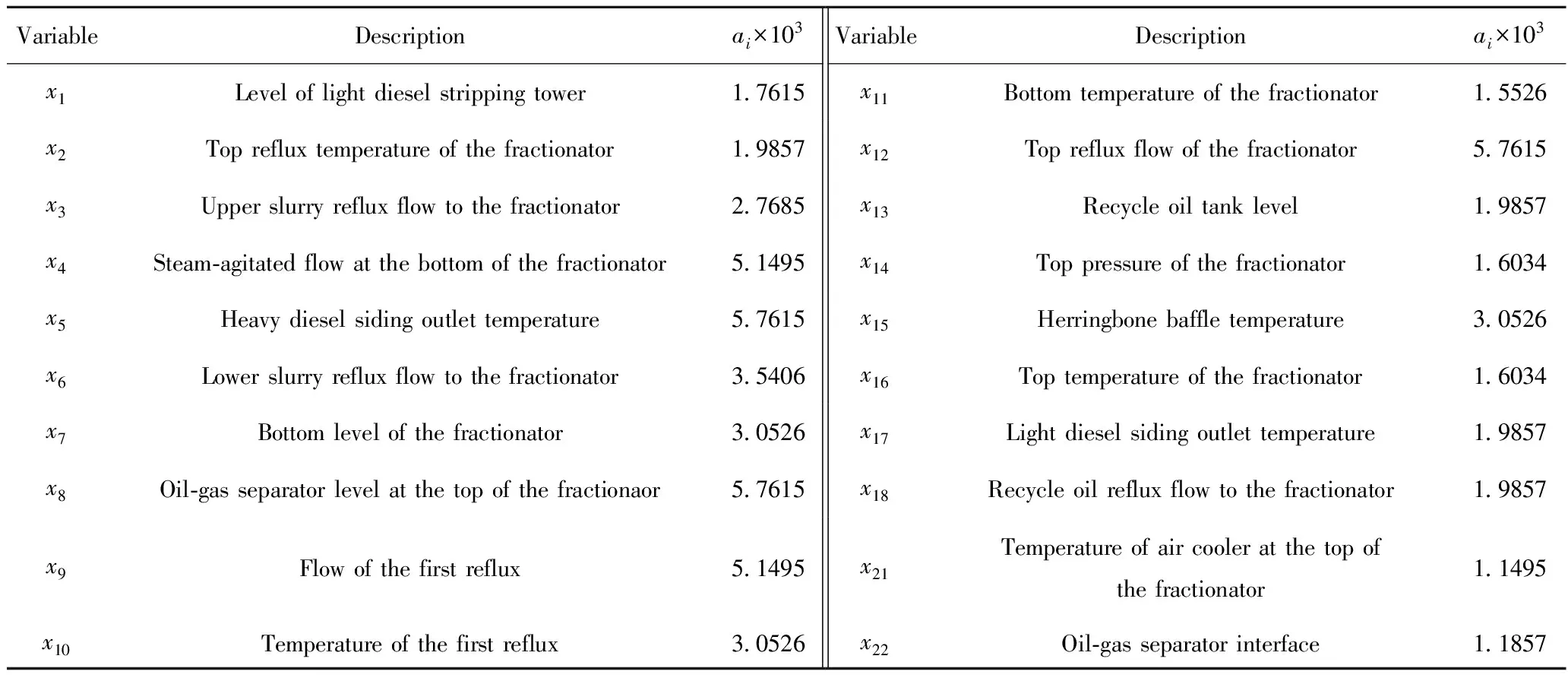
表3　待选风险表征指标Table 3　Possible risk indicators

因受风险影响较大的变量必然会产生明显的扰动，可根据其扰动变化趋势的大小进一步确定过程风险表征指标。这里采用最小二乘线性拟合方法对上述不同尺度下的待选风险表征指标在每次风险发展过程中前、后10 min内(采样间隔为5 s)的数据进行拟合，并以所求斜率绝对值的平均值作为该变量的扰动变化率(计算如式(8))，如表3所示，其大小可近似反映变量的扰动变化趋势，若扰动变化率过小，说明该变量并未产生大的波动，即无法较好的表征风险发展过程。因此若扰动变化率小于某一阈值(这里根据专家经验设为1.5×10-3)时，不使用相应的变量作为冲塔风险表征指标。

通过上述步骤，即可确定单元级中尺度下的冲塔风险表征指标，如表4所示。

表4　小尺度及中尺度冲塔风险表征指标Table 4　Risk indicators of small scale and mesoscale

分馏塔本身属小尺度研究范围，若仅从小尺度考虑时，冲塔风险表征指标包括表4中的分馏塔顶压力、分馏塔塔底液位、分馏塔塔顶温度、分馏塔塔底搅拌蒸汽流量、分馏塔底温度、人字挡板上温度、重柴油侧线馏出口温度及轻柴油侧线馏出口温度。

4.2　分馏塔冲塔风险因果图的建立

表4列出了小尺度及中尺度的冲塔风险表征指标，基于互相关函数计算并结合过程知识建立冲塔风险因果图。

4.2.1中尺度冲塔风险因果图的建立

首先，通过式(1)计算过程风险表征变量间考虑时延性的关联函数值，并通过式(2)和式(3)得到过程变量间时滞以确定风险传播方向。通过式(4)可确定两变量间的时延关联系数，如果关联系数没有通过显著性检验式(5)，两变量间的关联性将没有意义。此外，通过式(6)式(7)进一步确定两变量因果关系的显著性，从而构造出时滞矩阵L和关联系数矩阵P：

过程变量个数n为18，时间序列长度N为300。基于时滞矩阵L和关联系数矩阵P，建立冲塔风险过程扰动传播因果图，并结合过程知识检验传播路径的合理性，对因果图进行修正，结果如图4 所示。

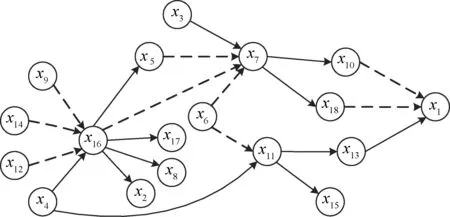
图4　中尺度冲塔风险过程扰动传播因果图Fig.4　Cause and effect diagram of risk disturbancepropagation in mesoscalexi(i=1,2,…18) represents the ith process variable node corresponding to the risk indicators of mesoscale in Table 4 respectively The dotted lines indicate a negative correlation between two variables;The solid lines indicate a positive correlation between two variables

4.2.2小尺度冲塔风险因果图的建立

根据设备级小尺度的冲塔风险表征指标，如表4 所示，同理，基于互相关函数计算并结合过程知识建立小尺度冲塔风险过程扰动传播因果图，如图5所示。

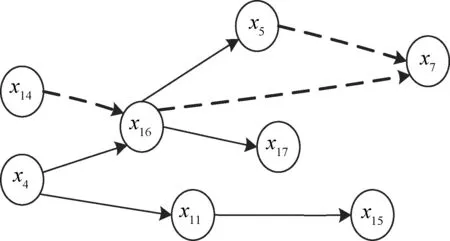
图5　小尺度冲塔风险过程扰动传播因果图Fig.5　Cause and effect diagram of riskdisturbance propagation in small scalexi represents the ith process variable node corresponding to the risk indicators of small scale in Table 4 respectively The dotted lines indicate a negative correlation between two variables;The solid lines indicate a positive correlation between two variables

4.3　分馏塔冲塔风险报警根源搜索

以发生在某石油化工企业的分馏塔冲塔事件为例，采用所提报警根源搜索方法进行分析。2016年7月24日，某石油化工企业催化裂化分馏塔发生冲塔，经现场人员调查分析，冲塔发生原因为一中回流泵故障，引起一中回流量过低，使得分馏塔塔顶温度升高，重柴油侧线馏出口温度升高，从而引起塔底液位发生低报警。

4.3.1中尺度冲塔风险报警根源搜索

下面首先基于单元级中尺度的冲塔风险过程扰动传播因果图，进行报警根源搜索分析，如图6所示。

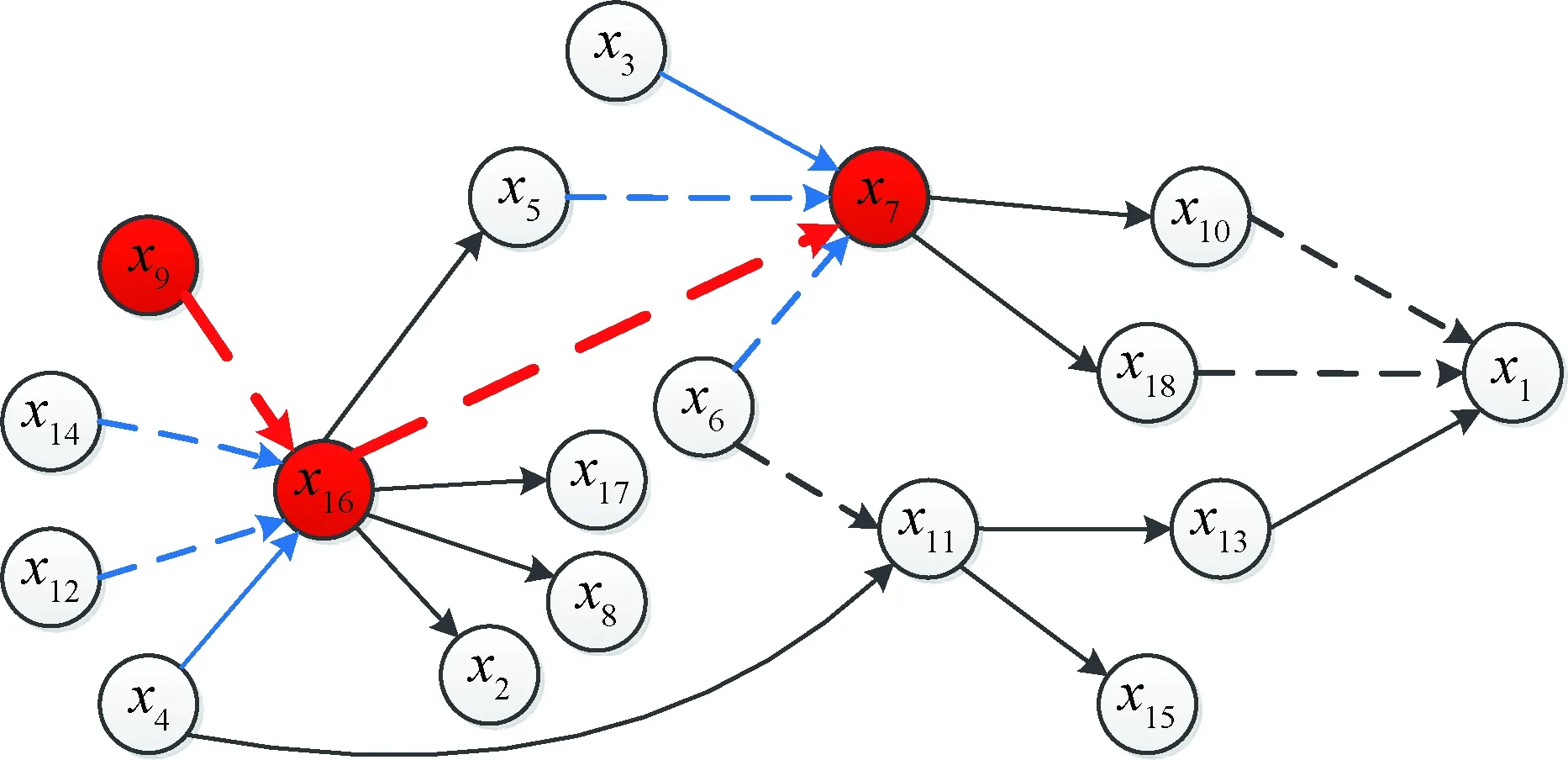
图6　中尺度冲塔风险过程报警根源搜索图Fig.6　The searching map for alarm root cause ofthe risk process in mesoscalexi(i=1,2,…18) represents the ith process variable node corresponding to the risk indicators of mesoscale in Table 4 respectively The dotted lines indicate a negative correlation between two variables;The solid lines indicate a positive correlation between two variables

步骤1：因分馏塔塔底液位(x7)发生报警，所以将其作为下级变量，根据因果图搜索与其直接相连的所有上级变量包括油浆下返塔流量(x6)、油浆上返塔流量(x3)、重柴油侧线馏出口温度(x5)和分馏塔塔顶温度(x16)。

步骤2：根据式(8)可得这些上级变量的扰动变化率如表5所示。

步骤3：通过比较各相关上级变量的扰动变化率

的绝对值，其最大值为3.5×10-3，对应x16，大于阈值C(这里根据专家经验设为1.5×10-3)，将上级变量x16作为其可能的上级原因变量。

步骤4：进一步确定该上级变量x16的变化趋势是否与两变量x7和x16间的正负相关关系一致。从图中可辨识出x7与x16负相关，因分馏塔塔底液位(x7)降低发生低报警，且所求x16的变化率为正，即分馏塔塔顶温度升高，与两变量间的正负相关关系一致，因此将上级变量分馏塔塔顶温度(x16)作为上级原因变量。继续搜索x16的上级变量包括一中回流量(x9)、分馏塔顶压力(x14)、分馏塔顶循环油流量(x12)和分馏塔塔底搅拌蒸汽流量(x4)，根据式(8)可得这些上级变量的扰动变化率如表5所示，通过比较各相关上级变量的扰动变化率的绝对值，其最大值为3.3×10-3，对应x9，大于阈值C=1.5×10-3，因x16与x9负相关，所求x9的变化率为负，x16的变化率为正，与变量间的正负相关关系一致，因此将上级变量一中回流量(x9)作为上级原因变量，因x9无上级变量，所以一中回流量过低即为报警的根本原因，而一中回流量过低是由一中回流泵故障引起，该结论与现场人员调查分析所得的冲塔发生原因一中回流泵故障一致。

表5　各上级变量的扰动变化率Table 5　The disturbance rate of each parent variable

4.3.2小尺度冲塔风险报警根源搜索

下面基于设备级小尺度的冲塔风险过程扰动传播因果图，进行报警根源搜索分析，如图7所示。

步骤1：因分馏塔塔底液位(x7)发生报警，所以将其作为下级变量，根据因果图搜索与其直接相连的所有上级变量包括重柴油侧线馏出口温度(x5)和分馏塔塔顶温度(x16)。

步骤2：根据式(8)可得这些上级变量的扰动变化率如表6所示：

步骤3：通过比较各相关上级变量的扰动变化率的绝对值，其最大值为3.5×10-3，对应x16，大于阈值C=1.5×10-3，将上级变量x16作为其可能的上级原因变量。

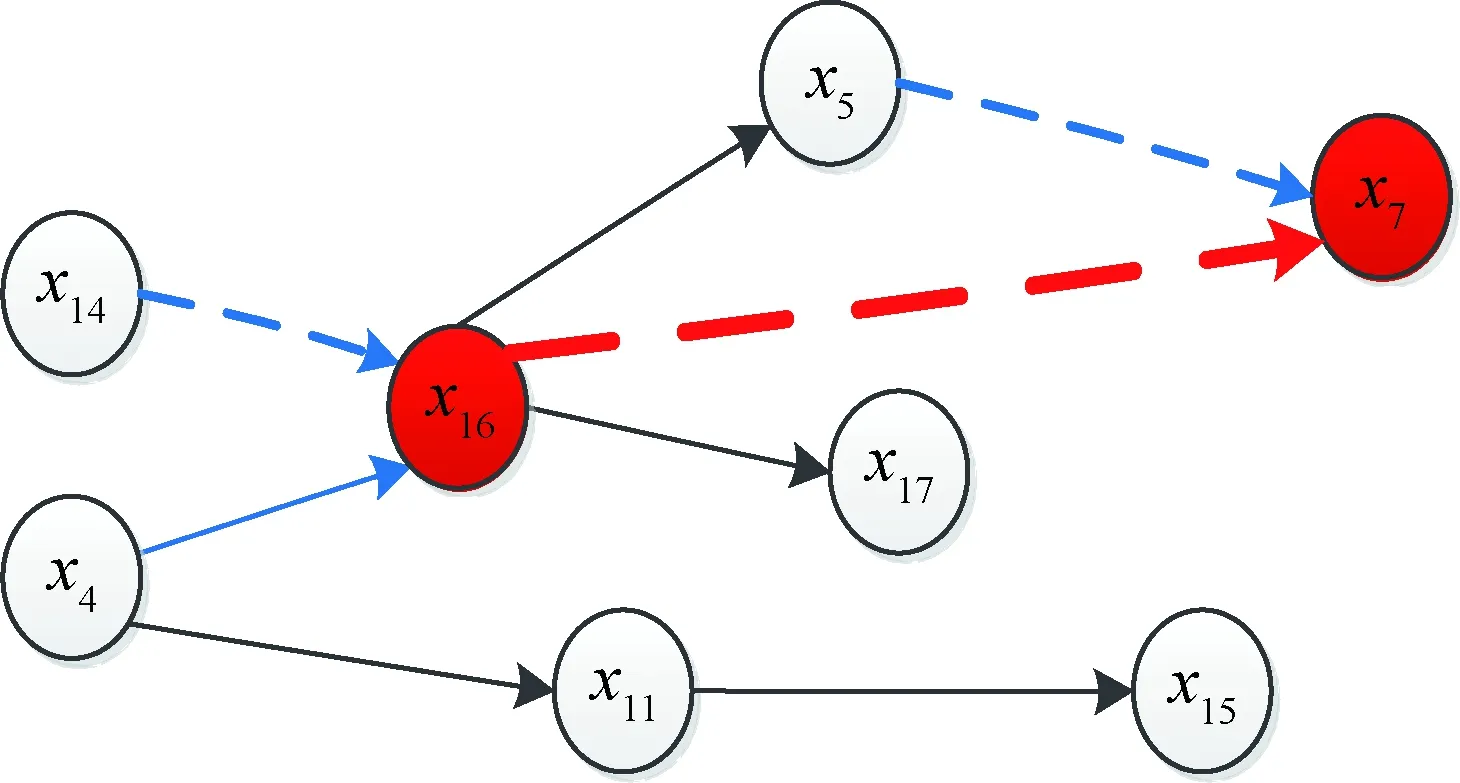
图7　小尺度冲塔风险过程扰动传播因果图Fig.7　The searching map for alarm root cause ofthe risk process in small scalexi represents the ith process variable node corresponding to the risk indicators of small scale in Table 4 respectively The dotted lines indicate a negative correlation between two variables;The solid lines indicate a positive correlation between two variables

表6　各上级变量的扰动变化率Table 6　The disturbance rate of each parent variable

步骤4：从图中可辨识出x7与x16负相关，因分馏塔塔底液位(x7)降低发生低报警，且所求x16的变化率为正，即分馏塔塔顶温度升高，与变量间的正负相关关系一致，因此将上级变量分馏塔塔顶温度(x16)作为上级原因变量，继续搜索x16的上级变量包括分馏塔顶压力(x14)和分馏塔塔底搅拌蒸汽流量(x4)，根据式(8)可得这些上级变量的扰动变化率如表6所示，通过比较各相关上级变量的扰动变化率的绝对值，其最大值为1.4，小于阈值C=1.5×10-3，因此该最大值对应的上级变量分馏塔塔底搅拌蒸汽流量(x4)不再被考虑，搜索终止，所以分馏塔塔顶温度(x16)过高即为报警的根本原因，该结论与现场人员调查分析所得的冲塔发生原因一中回流泵故障并不一致，即从设备级小尺度上进行分析并未辨识出引发报警的根本原因。

5　结　论

通过对炼油化工生产系统的空间尺度进行划分，采用多尺度建模的方法，针对分馏塔冲塔风险过程，分析其不同尺度下的过程风险表征指标，建立多尺度下的冲塔风险报警根源分析模型，并对不同尺度下的模型进行应用对比分析，从而选择合适的尺度进行建模，保证炼油化工过程报警根源分析的准确性。

对于过程风险报警根源分析而言，需对整个风险单元进行分析，仅考虑与风险直接相关的设备可能遗漏某些重要原因变量，以致无法推绎出引发报警的扰动根源。

对于炼油化工过程风险状态监测及故障诊断而言，选择合适的尺度进行建模分析，同样有助于保证过程风险状态监测及故障诊断的准确性。

对于存在反馈控制的复杂过程，可能会出现闭环问题，未来将进一步研究存在闭环问题的炼油化工过程报警根源分析。

[1] DAHLSTRAND F. Consequence analysis theory for alarm analysis[J]. Knowledge-Based Systems, 2002, 15(1): 27-36.

[2] WAN Y, YANG F, LÜ N, et al. Statistical root cause analysis of novel faults based on digraph models[J]. Chemical Engineering Research and Design, 2013, 91(1): 87-99.

[3] YANG F, SIRISH L S, XIAO D. 2010 Conference on Control and Fault-Tolerant Systems (SysTol)[C]//France：IEEE, 2010： 387-392.

[4] MAURYA M R, RENGASWAMY R, VENKATASUBRAMANIAN V. A systematic framework for the development and analysis of signed digraphs for chemical processes 1 Algorithms and analysis[J]. Industrial & Engineering Chemistry Research, 2003, 42(20): 4789-4810.

[5] MAURYA M R, RENGASWAMY R, VENKATASUBRAMANIAN V. A systematic framework for the development and analysis of signed digraphs for chemical processes 2 Control loops and flow sheet analysis[J]. Industrial & Engineering Chemistry Research, 2003, 42(20): 4811-4827.

[6] 李安峰， 夏涛， 张贝克， 等. 化工过程SDG建模方法[J].系统仿真学报， 2003, 15(10): 1364-1368. (LI Anfeng, XIA Tao, ZHANG Beike, et al. SDG modeling approach for chemical engineering process[J]. Journal of System Simulation, 2003, 15(10): 1364-1368.)

[7] 王伟， 于达仁， 赵辉， 等. 基于符号有向图模型的故障诊断方法[J].动力工程学报， 2007, 27(5): 736-741. (WANG Wei, YU Daren, ZHAO Hui, et al. Fault diagnosis method based on sign directed graph models[J]. Journal of Power Engineering, 2007, 27(5): 736-741.)

[8] 朱群雄， 高慧慧， 刘菲菲， 等. 过程工业报警系统研究进展[J].计算机与应用化学， 2014, 31(2): 129-134. (ZHU Qunxiong, GAO Huihui, LIU Feifei, et al. Research progress of alarm systems in the process industries[J]. Computers and Applied Chemistry, 2014, 31(2): 129-134.)

[9] BAUER M, THORNHILL N F. A practical method for identifying the propagation path of plant-wide disturbances[J].Journal of Process Control, 2008, 18(7): 707-719.

[10] DUAN P, YANG F, CHEN T, et al. American Control Conference (ACC)[C]//Canada： IEEE, 2012： 3522-3527.

[11] BAUER M, COX J W, CAVENESS M H, et al. Finding the direction of disturbance propagation in a chemical process using transfer entropy[J].IEEE Transactions on Control Systems Technology, 2007, 15(1): 12-21.

[12] ABELE L, ANIC M, GUTMANN T, et al. Combining knowledge modeling and machine learning for alarm root cause analysis[J].IFAC Proceedings Volumes, 2013, 46(9): 1843-1848.

[13] HAN L, GAO H, XU Y, et al. Combining FAP, MAP and correlation analysis for multivariate alarm thresholds optimization in industrial process[J].Journal of Loss Prevention in the Process Industries, 2016, 40: 471-478.

[14] GAO J, TULSYAN A, YANG F, et al. A transfer entropy method to quantify causality in stochastic nonlinear systems[J].IFAC Proceedings Volumes, 2016, 49(7): 454-459.

[15] GAO H, XU Y, GU X, et al. Systematic rationalization approach for multivariate correlated alarms based on interpretive structural modeling and Likert scale[J].Chinese Journal of Chemical Engineering, 2015, 23(12): 1987-1996.

[16] PENG D, GU X, XU Y, et al. Integrating probabilistic signed digraph and reliability analysis for alarm signal optimization in chemical plant[J].Journal of Loss Prevention in the Process Industries, 2015, 33: 279-288.