“嫦娥4号”中继星任务轨道确定问题初探

段建锋，刘勇，李勰，陈明，王兆魁

（1.清华大学 航天航空学院，北京 100084；2.北京航天飞行控制中心，北京 100094；3.航天飞行动力学实验室，北京 100094）

引 言

月球探测是人类了解地球、太阳系和宇宙的第一步。人类通过月球探测可以研究太阳系及宇宙的起源、演变和现状，进一步认识地球环境的形成和演变，认识空间现象和地球自然系统之间的关系，从现实和长远来看，对月球的探测和开发具有十分重要的科学和经济意义[1]。

20世纪90年代，我国已经开始进行月球探测工程的先期研究。我国的探月工程，在2020年前分“绕”“落”“回”三步实施，所谓“三步走”战略[2]。我国第一个月球探测器“嫦娥1号”卫星于2007年10月成功环月探测，圆满实现了探月工程一期“绕”的目标[3]；2010年10月，“嫦娥2号”卫星作为探月工程二期任务的先导星，成功完成了环月的先导探测，并完美地完成了多阶段拓展任务，通过一次发射任务完成了月球、日地拉格朗日L2点、“图塔蒂斯”小行星的多目标探测[4]；2013年12月14日，“嫦娥3号”探测器成功着陆月球虹湾地区，12月15日，“玉兔号”月球车与着陆器顺利分离，其行走的车辙印在了月球表面。“嫦娥3号”成功地完成了任务，首次实现了我国航天器在地外天体软着陆和巡视勘察，标志着我国探月工程第二步战略目标的全面实现。2014年11月1日，“嫦娥5T1”高速再入试验任务的返回器在内蒙古四子王旗地区顺利着陆，标志着我国月球探测领域技术的又一次重大进步，拉开了我国探月工程第三期的序幕[5]。

“嫦娥4号”任务分为中继星任务和探测器任务2个阶段，中继星被命名为“鹊桥”，于2018年5月21日发射升空，于2018年6月中旬进入绕地月L2点Halo轨道上，2018年12月8日发射的着陆器和巡视器组合将利用中继星实现月球背面的数据通信，为其在月球背面的软着陆和巡视奠定基础，因此，中继星任务成败决定着“嫦娥4号”任务的成败。在世界深空探测任务中，从未在地月L2点部署一颗中继星，其具有任务轨道新、在轨时间长、轨道精度要求高等特点，面对新任务，作为测控系统重要环节的探测器轨道计算工作需在原有深空探测精密轨道确定工作的基础上开展进一步的研究。

本文着眼于2018年“嫦娥4号”任务的全面执行，重点针对任务中先行发射的中继星任务轨道确定问题开展工作，基于中继星使命轨道特性和定轨摄动影响因素的初步分析，确定太阳光压为其主要的定轨预报误差影响源。在太阳光压球模型的基础上，结合中继星构型特点，开展太阳光压等效面积的建模求解，经仿真分析，使用改进后的太阳光压球模型进行定轨，速度精度可提升约一个量级。

1 中继星任务使命轨道动力学模型

1765年，欧拉（Euler）发现了在一个旋转二体重力场中存在3个共线的天平动点。1772年，拉格朗日（Lagrange）指出在一个旋转二体重力场中存在另外2个天平动点，后人将这5个点统称为拉格朗日点，也称平动点[6-7]。平动点是第三体在受两个大天体的万有引力作用时，在空间中的引力平衡点。运行于平动点的飞行器可以保持该双星系统的公转角速度而几乎不用消耗推进剂。由于平动点特殊的动力学特性和在三体问题中相对固定的位置，使其在停泊中转、中继通信、星际转移等未来深空探测任务中具备较好的工程应用价值[8-11]。

三体问题地月L2点附近存在Halo轨道、李雅普诺夫轨道、轴向轨道、垂直轨道、蝶形轨道等周期轨道以及李萨如（Lissajous）非周期轨道。根据轨道设计的分析情况，在地月系中，面向“嫦娥4号”任务中支持月球背面中继通信的工程需求，Halo轨道和Lissajous轨道较合适，在文献[12]中，刘磊等提出Lissajous的轨道维持控制优于Halo轨道，但是对于Lissajous轨道而言，其轨道在会合坐标系下呈Lissajous曲线的形式，虽然可以通过选取初始相位和轨道振幅使航天器尽量避开月掩带，但在长时间飞行的情况下仍然难以避免月掩的出现[13]。因此，考虑到其长期地月通讯的需求，中继星标称使命轨道类型采用Halo轨道。

中继星由“长征4号”丙运载火箭（Chang Zheng-4C，CZ-4C）运载火箭发射升空，送入倾角28.5°、近地点高度200 km、远地点高度约40万km的地月转移轨道，在地面测控支持下，经中途修正，在近月点实施近月制动和月球借力后，进入月球至地月L2点的转移轨道，经地月L2点捕获后，进入环绕地月L2点的使命轨道[14]。

中继星在使命轨道运行期间，其加速度可描述为

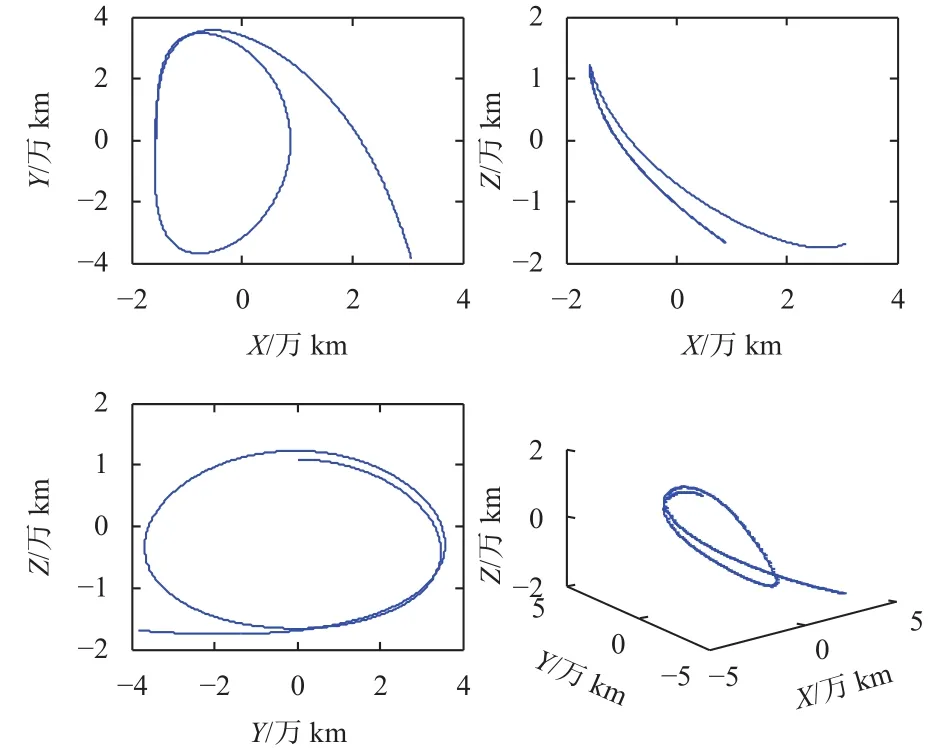
图1 Halo轨道受光压影响不稳定性示意图Fig.1 Instability of Halo orbit affected by Solar pressure

2 定轨误差源影响分析

中继星运行于绕地月L2点的Halo轨道上，根据动力学模型分析，其主要受太阳、地球、月球三体引力作用，太阳光压对其影响亦较为明显。Halo轨道不稳定，在无轨道机动作用下，使用“嫦娥4号”中继星标称的使命段轨道根数作为仿真的起始轨道，在图1中，航天器运行1圈（约14天）后将偏离Halo轨道。

针对Halo轨道的不稳定性特点，地面运控将采用约7天进行一次轨道维持的策略对其进行轨道保持。轨道确定精度的提升将有利于延长轨道维持的周期，可节省地面大量的人力物力及星上能源。为针对性地采取措施提升定轨精度，需通过仿真分析获取各摄动力的量级，确定不同误差源对定轨精度产生的影响，为后续开展工作提供支撑。

2.1 仿真分析策略

2.1.1 仿真动力学模型

本文定轨预报分析工作是在北京航天飞行控制中心研制开发的轨道计算与分析软件平台[16]（Beijing Orbit Determination and Analysis Software，BODAS）基础上开展的，仿真动力学模型如表1所示，太阳光压模型使用的是球模型，月球重力场采用精度较高的GL0420A模型[17]。

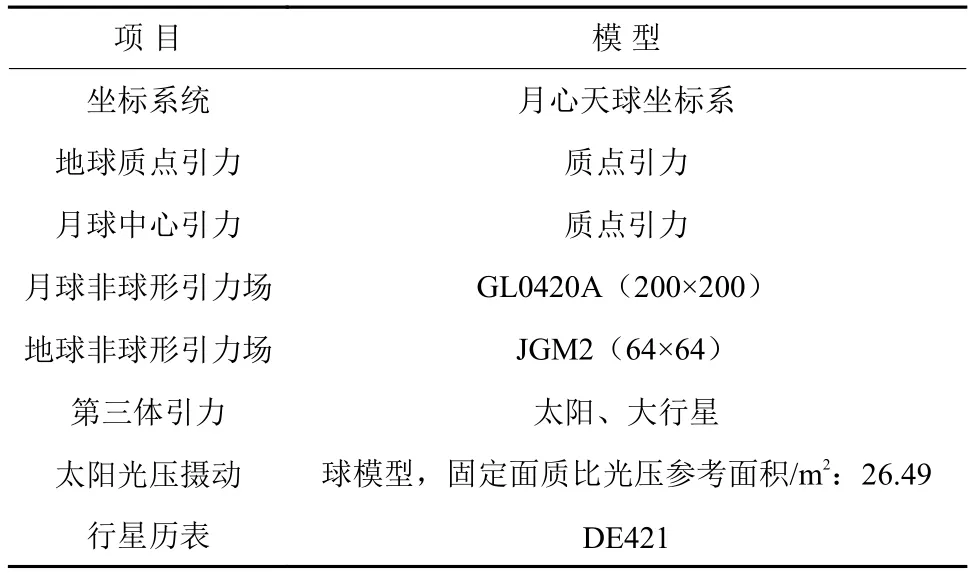
表1 仿真模型参数使用Table 1 Dynamic model parameters used in simulation

2.1.2 仿真分析方案

选择中继星刚进入使命轨道时标称的位置速度作为仿真的初始轨道，参与仿真的测站包括佳木斯、喀什、南美深空站，上海、北京、昆明及乌鲁木齐甚长基线干涉测量技术（Very Long Baseline Interferometry，VLBI）站，测站跟踪条件及测量精度设置如表2所示。基准星历为综合考虑较高精度动力学模型的基础上外推而得。如表3所示的仿真设定方案中，通过不同参数的设定，寻找影响Halo轨道定轨预报精度的最大误差源。不失一般性，仿真时间限定在2018-06-16T11:00:30—2018-06-22T11:00:30区间。

表2 测站跟踪条件及测量精度Table 2 Tracking conditions and measuring accuracy of stations

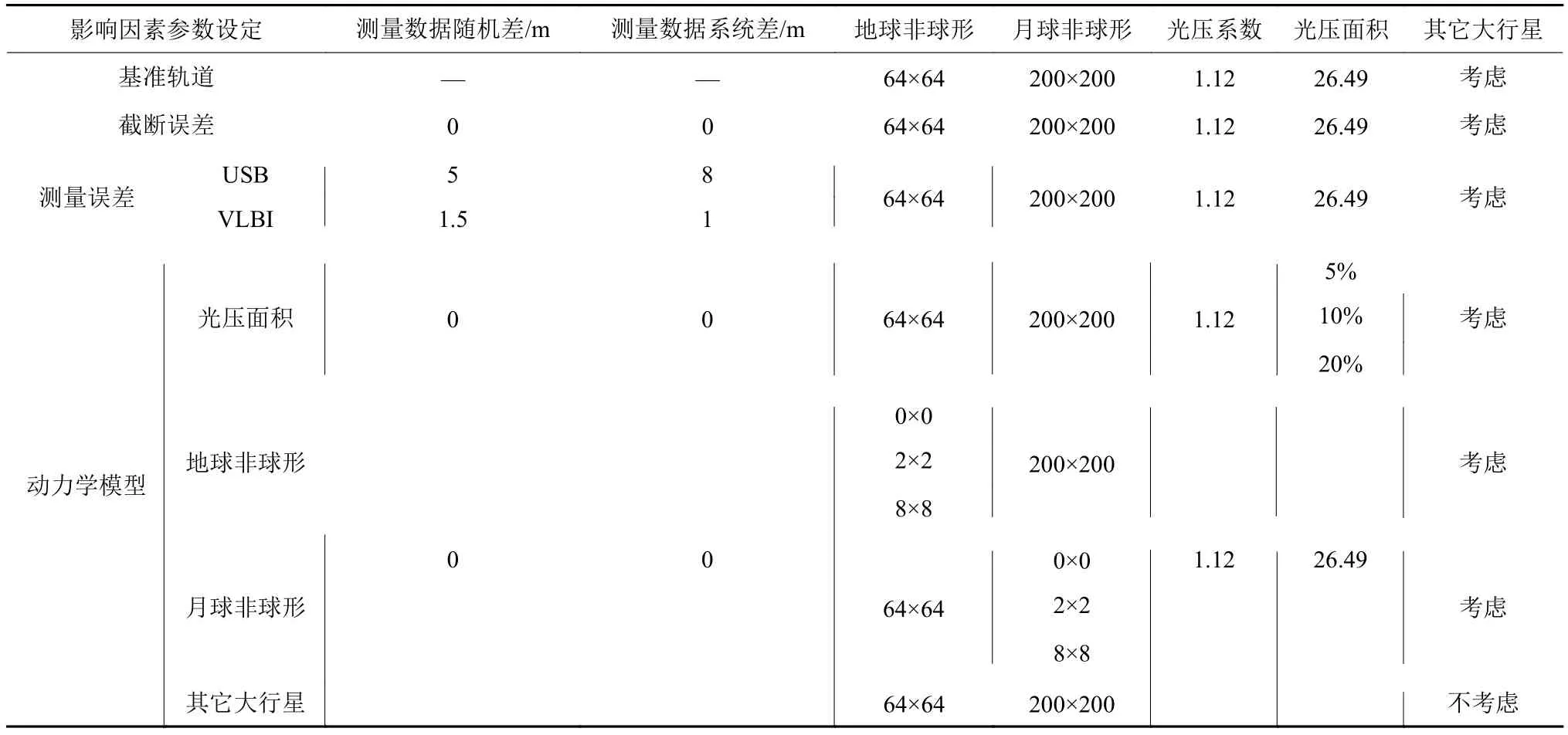
表3 仿真想定方案Table 3 Simulation scheme

2.2 仿真分析结果

根据如表1所示的参数设置，在标称轨道的基础上预报6天后的轨道摄动力分析结果如图2所示，中继星在绕L2点使命轨道上飞行时，太阳、地球、月球的质点引力为主要的影响力，其余为摄动力，其中光压的摄动影响最大，达到10-7m/s2量级，是无法忽视的，地球和月球J2项的影响量级与木星、火星等其他大行星的摄动影响量级均小于10-9m/s2，并不是影响轨道的主要因素。

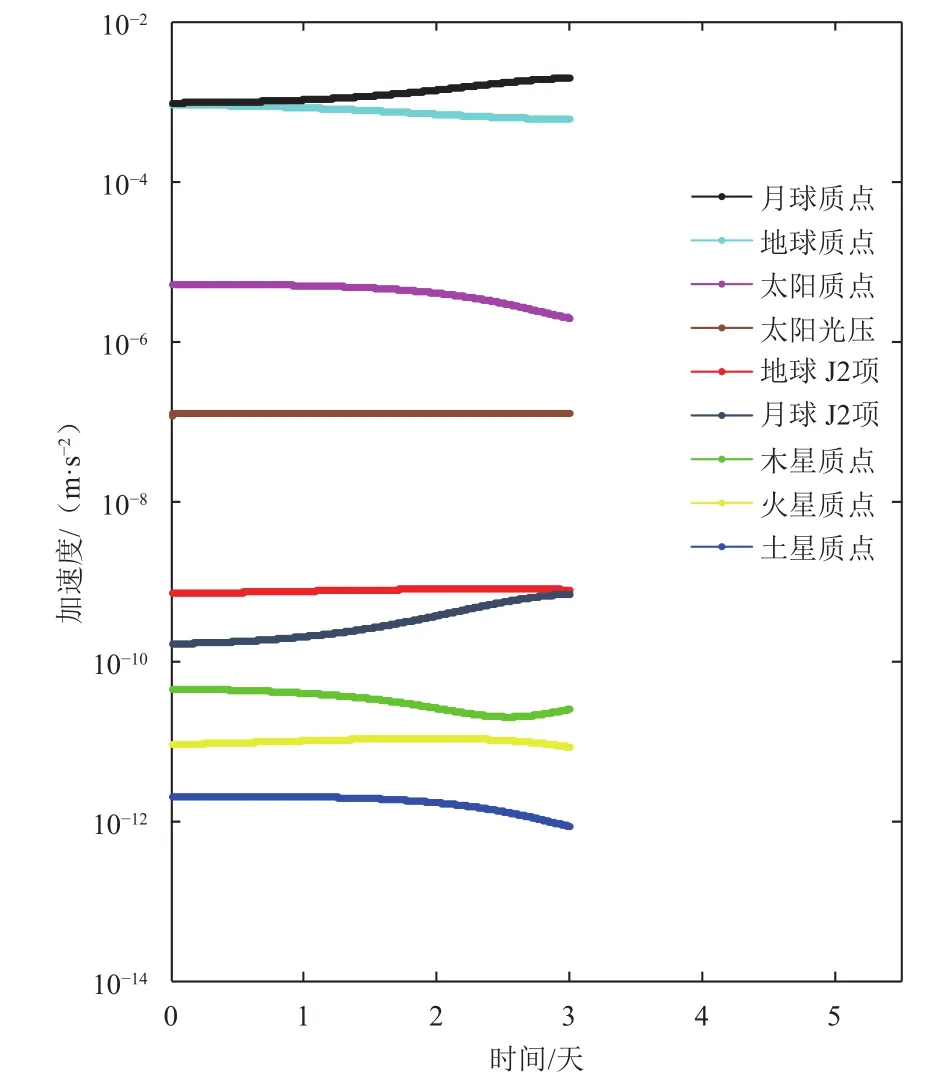
图2 中继星使命轨道段轨道摄动量级分析Fig.2 Orbital perturbation level of relay satellite in mission orbit

误差源分析仿真结果如表4所示，由表4可知:定轨预报系统在计算时因计算机有效位的限制所造成的截断误差所产生的位置误差为毫米量级，速度误差为10-5mm/s的量级，对轨道的影响不大；地球及月球的非球形引力对绕飞地月L2点的中继星轨道影响有限，若在定轨预报中不考虑两者影响，预报6天的时间，将产生50 m以内的位置误差，考虑2阶或者2阶以上，预报6天的位置误差在厘米甚至毫米量级；在考虑如表2所示的测量误差基础上，预报所产生的位置误差为20 m；若不考虑如木星、火星等其他大行星摄动，产生的位置误差为5 m，分别考虑光压等效面积5%、10%、20%误差的情况下，预报6天所产生的位置误差最大分别达250、500、1 000 m，均远大于其他影响因素所产生的误差，由此可得，中继星在使命轨道稳定飞行期间，太阳光压摄动是定轨预报精度的主要影响因素。

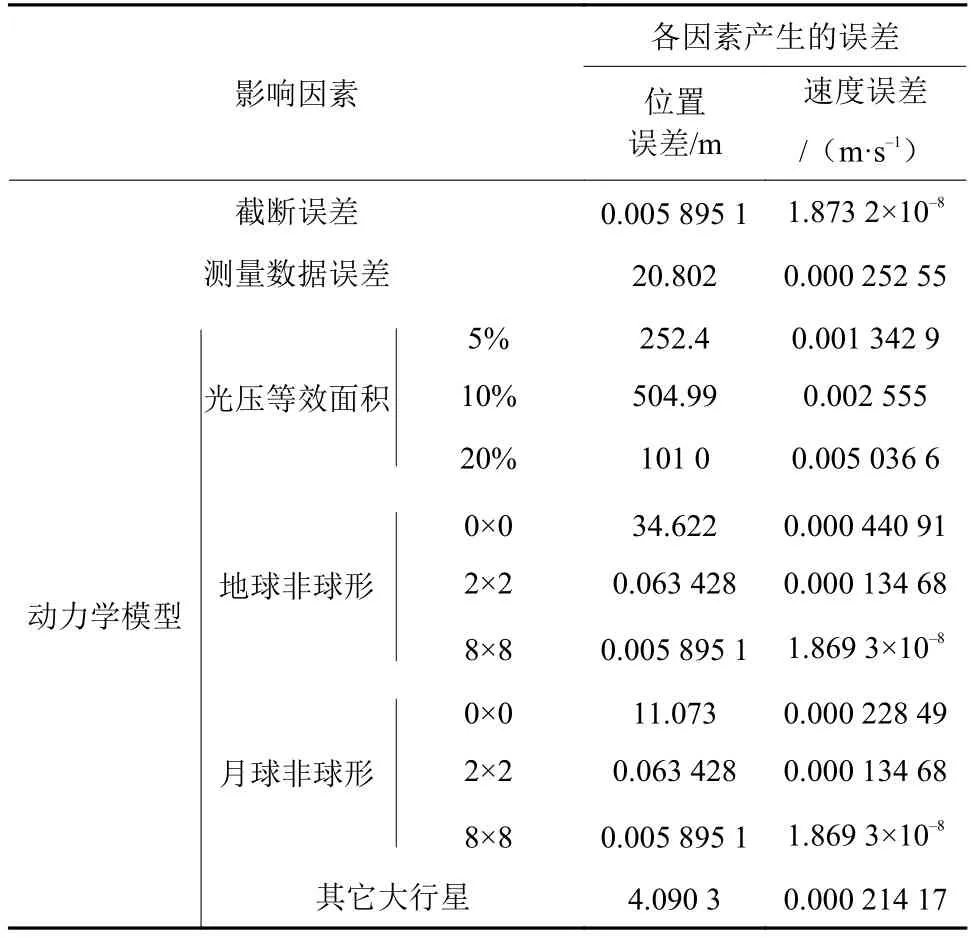
表4 误差源分析结果Table 4 Analysis results of error sources

3 中继星光压面积求解

根据第3节中仿真分析的结果，当中继星在地月L2点绕飞时，光压摄动对其有重要影响，中继星为满足远距离中继通信需求，卫星本体上安装了一个大型的抛物面天线，且在执行中继通信任务期间，卫星与太阳矢量的夹角并不固定，在使用球模型的前提下，光压等效面积是实时变化的，为提高轨道确定过程中的精度，需对其进一步分析处理。

3.1 太阳光压模型

太阳光压模型一般分为经验型、分析型和半经验半分析型模型，其中球模型作为经典的分析型光压模型，在深空探测中被广泛应用。对太阳光压进行建模时，将卫星简化为一个球体，在这种假设条件下，太阳光压模型可以表示为

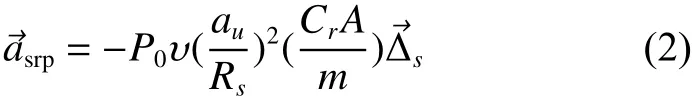
其中:P0为距太阳1天文单位处的光压强度，近似值为4.560 5×10-6N/m2；au为天文单位，等于1.496×1011m；Rs为卫星到太阳的距离；为卫星指向太阳的单位矢量；υ为地影因子，介于0～1之间；Cr为卫星本体的光压系数，与卫星表面材料的物理特性有关；A为卫星本体在太阳方向的有效截面积，与卫星本体的几何形状和卫星姿态有关；m为卫星质量[18]。

3.2 中继星构型特点及其三轴与太阳矢量的关系

中继星构形设计继承了CAST100平台卫星构形设计的特点，整星的构形基本为一立方体形状，卫星在轨飞行状态构形见图3所示，在其本体坐标系中，+Z轴为抛物面天线主轴，Y轴为太阳翼帆板所在轴，X轴与+Y、+Z轴构成右手系。

图3 中继星整体构型示意图Fig.3 The map of external structure of relay satellite

中继星运行在使命轨道上时，光照时间比例接近100%。中继星在任务轨道对月中继通信时，卫星+Z轴（天线轴）在惯性空间的指向为卫星指向目标探测器或者地球单位矢量，TZI；卫星+Y轴在惯性空间的指向为+Z轴矢量叉乘太阳矢量，TYI=TZI×SI，SI为太阳矢量；卫星+X轴符合右手定则，如图4所示。

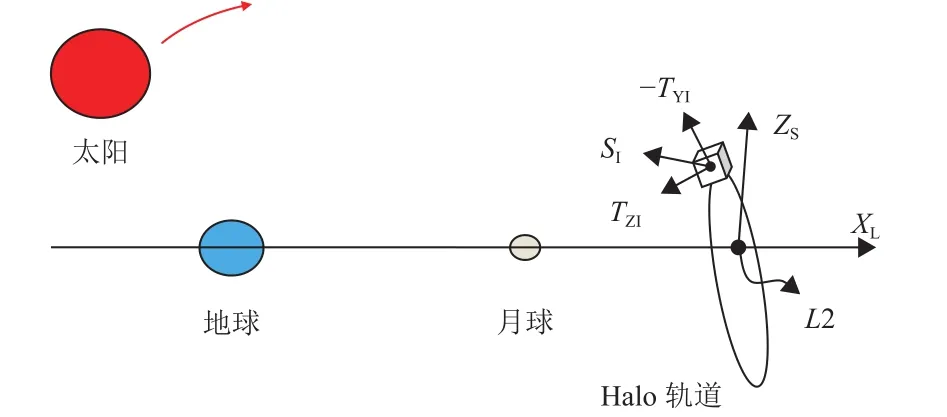
图4 目标姿态定义示意图Fig.4 The attitude of relay satellite in Halo orbit

因此，卫星对月或对地定向时，能确保中继星+Y轴即太阳帆板与太阳矢量垂直，即夹角为90°；中继星－X轴与阳光的夹角均大于90°，即－X面不会被阳光照到。

3.3 中继星光压面积的建模求解

当中继星在轨运行时，其主要使命是中继通信，卫星本体的+Z轴指向着陆区，导致其与太阳矢量的夹角α在[0,180°]将随时间变化，对应的光压面积A也将随时间变化，该变化具有连续性和周期性的特点，在无法获知卫星模型详细参数的情况下，数学表达式的求解较为困难。为简化问题，本文通过求解卫星+Z轴与太阳矢量夹角α在特定值下的太阳光压面积，采取插值的方式获取α角与光压面积A之间的数值关系。

根据中继星在Halo轨道的运行规律及其星体结构特点，可以选取的α角特征点如表5所示，其中68.7°、111.3°分别表示太阳沿抛物面天线的母线顺射和逆射时与卫星+Z轴的夹角，5个特征点的三维示意图如图5所示，图5中正面均为太阳入射方向。在面积求解时，考虑抛物面天线具有70%透光率的特点，当α角为0°和180°时，抛物面天线等效为圆，在α角为90°时，抛物面天线等效为三角形，在α角为68.7°、111.3°时，抛物面天线等效为椭圆，根据卫星相关尺寸参数，计算可得如表5所示结果。

表5 α角特征点对应的中继星光压等效面积Table 5 Solar pressure equivalent area of relay star corresponding to alfa angular characteristic points

根据以上特征点的离散特征及中继星在轨运行是面积变化连续性特点，选择保形分段3次Hermit插值方法进行插值，以0.1°为间隔，插值结果可得如图6所示夹角α与光压等效面积得对应关系图，由图6可知，中继星的光压等效面积可由夹角α决定。

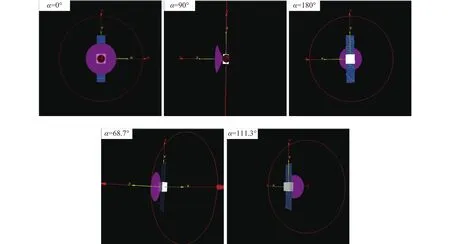
图5 中继星+Z轴与太阳矢量夹角α特征点示意图Fig.5 The operating state of relay satellite in different α

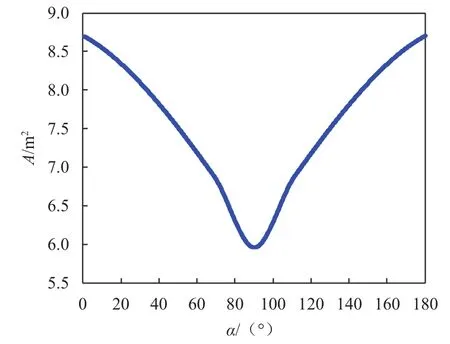
图6 中继星+Z轴与太阳矢量夹角α与光压等效面积的关系Fig.6 The change of effective illumination area A to angle α

4 仿真分析验证

为验证模型的正确性及有效性，在获取真实测量数据之前，运用仿真手段进行分析。假定卫星在使命轨道上进入中继通信模式，卫星+Z轴将保持对月状态，其中中继星+Z轴与太阳矢量夹角和光压等效面积的变化如图7所示。

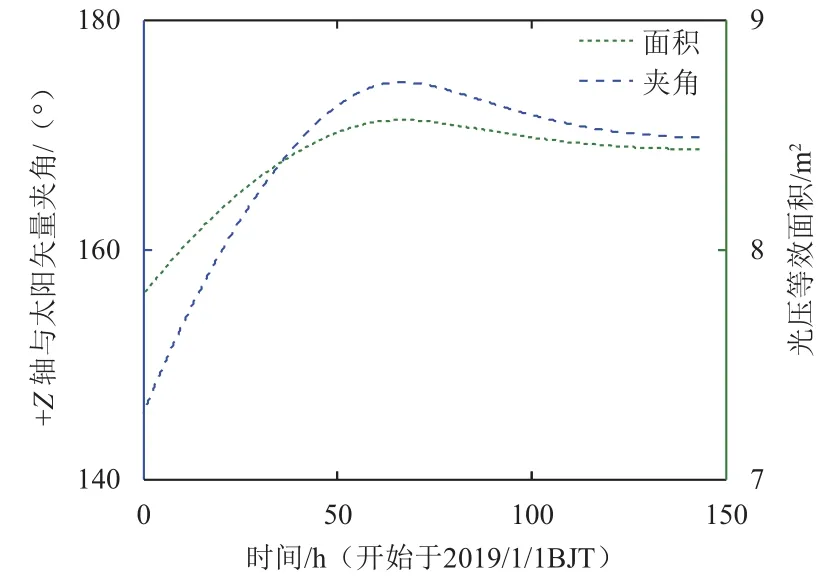
图7 中继星+Z轴与太阳矢量夹角α与光压等效面积的变化情况Fig.7 The change of effective illumination area A to angle α

结合本文第3节的仿真，使用6天的仿真数据基础上，分别在原有球光压模型和修正后的球光压模型下进行定轨求解，经比较分析，如图8所示，使用修正后的球光压模型后，在RTN（Radial-Track-Normal）轨道坐标系[19]下，6天时间的定轨位置可提升约3倍精度，速度可提升约1个量级的精度。

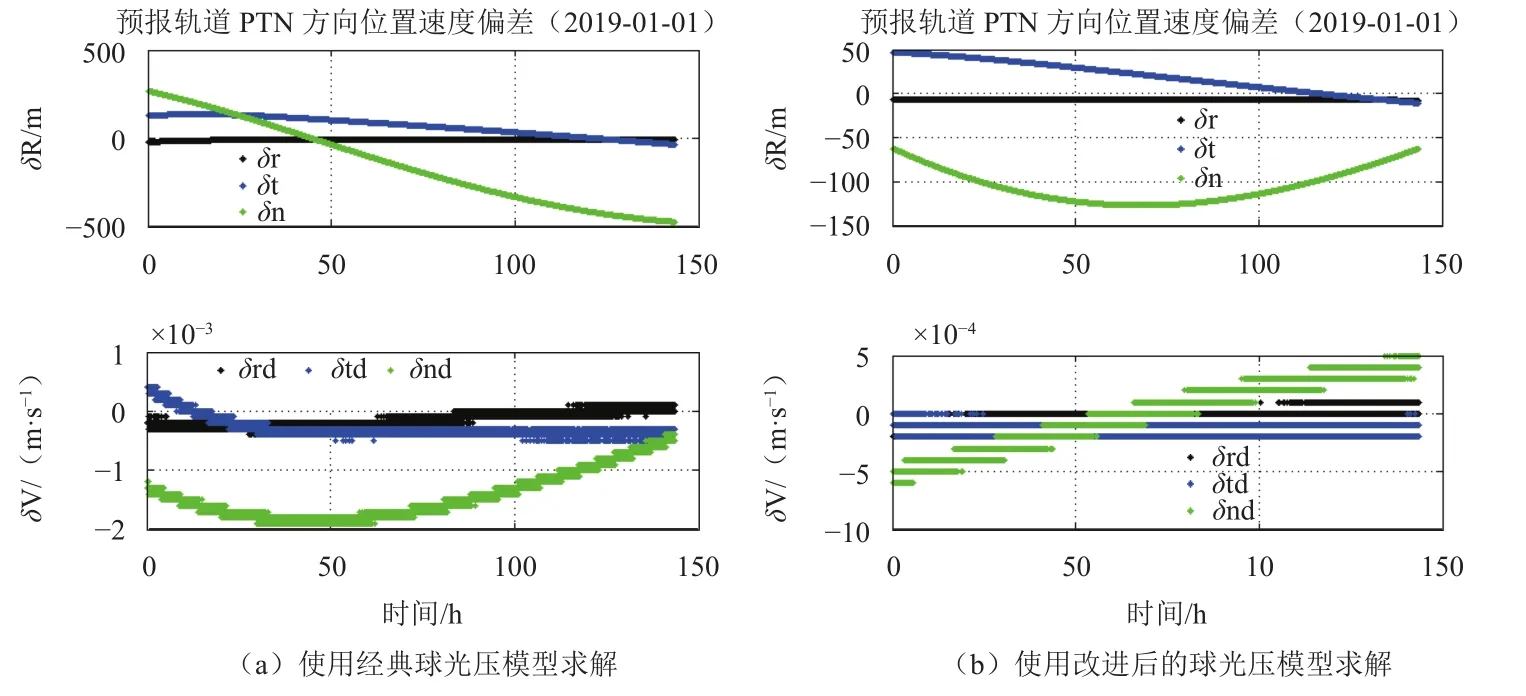
图8 定轨后星历比较结果Fig.8 Comparison results of ephemeris after orbit determination

5 结 论

“嫦娥4号”中继星任务的使命轨道是在综合考虑了任务设计需要的前提下，选定了Halo轨道作为其使命轨道，本文根据中继星在使命轨道段运行的动力学模型，在BODAS分析平台的基础上，进行了Halo轨道摄动力量级分析和定轨预报误差源的判定，结果均表明太阳光压摄动是影响其定轨预报误差的主要因素。

结合中继星运行构型及其运行姿态特点，光压面积受其本体系+Z轴和太阳矢量夹角α的影响，为简化计算，采用选取特征点后插值的方式获取其对应数值关系。经仿真分析，使用改进后的太阳光压模型进行定轨求解，中继星在地月L2点Halo轨道上的定轨速度精度可提升约一个量级，这对后续进一步开展中继星实测数据轨道确定精度分析奠定了基础。