Modeling and analysis of cloud computing system survivability based on Bio-PEPA

Zhao Guosheng　Ren Mengqi　Wang Jian　Liao Yiwei

(1College of Computer Science and Information Engineering, Harbin Normal University, Harbin 150025, China)(2School of Computer Science and Technology, Harbin University of Science and Technology, Harbin 150080, China)

Survivability refers to the capability of a system to fulfill its critical services in a timely manner when the system is subjected to external attacks, such as viruses or internal failures[1].Cloud computing is a new type of distributed network service computing model[2].A cloud computing system can provide a variety of trusted critical services for users.Therefore, it is extremely important to ensure that the critical services in the cloud computing system one executed continuously when the system is subjected to external attacks or internal failures.Recently, domestic and overseas scholars have conducted large-scale research on survivability, and the main research areas include the formal modeling, survivability enhancement technology, survivability analysis, test and evaluation, etc.

Chang et al.[3]proposed a solution for the virtual system survivability model, in which the continuous time Markov chain is used to analyze the service survivability after its failure.Using the proposed solution, the viability of the system can be quantitatively assessed.Jin et al.[4]considered the survivability of each node, the deletion of links and nodes determined by the survivability of the nodes, a survivable topology evolution model based on the wireless sensor network was proposed.Through this model, the survivability of the node can be analyzed.Zhou et al.[5]proposed a method to predict survivability according to a large amount of log audit data of the system, and used a quantitative method to analyze the survival ability of the system over a certain period of time.Alobaidi et al.[6]also proposed a quantitative analysis method based on the smart grid, which described the changes of the system state and the decline conditions in its service performance, in order to maintain the highest system survivability during the recovery process.

The above studies analyzed the survivability of the system or critical service by models which can quantitatively analyze the survivability, and then clearly depict the changing process of the survivability.However, their studies did not consider the dynamic impact conditions of the system survivability, such as external attacks or internal failures in the actual system operation.

In summary, based on the features of the biological immune system[7-8], on the basis of the SAIR model[9], the SEIRS model[10]and the vulnerability propagation model of distributed virtualization[11], the survivability evolution model of critical cloud services in the cloud computing system is obtained.

1　Bio-PEPA Syntax

Bio-PEPA (biological-performance evaluation process algebra)combines some features of biological network and is well suited to describing the spread of the virus within a cloud computing system and the survivability evolution of critical cloud services.The basic semantic expressions are as follows[12-13]:

S::=(α,γ)opS|S+S|Constant|S@L

(1)

op::=↓|↑|⊙

(2)

(3)

The meanings of the basic expressions are shown in Tab.1.

Tab.1　The meanings of Bio-PEPA basic expressions

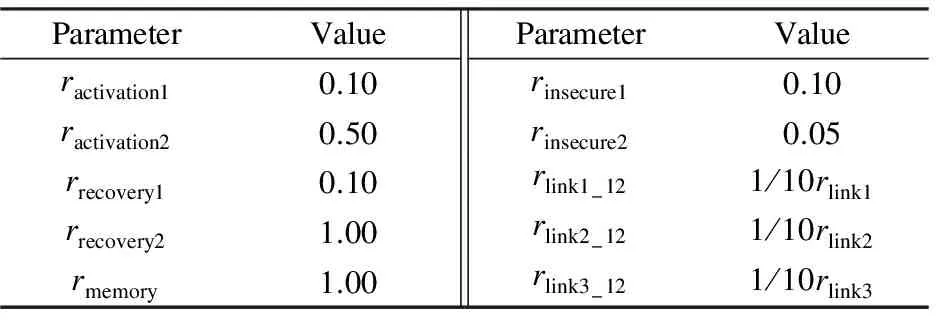
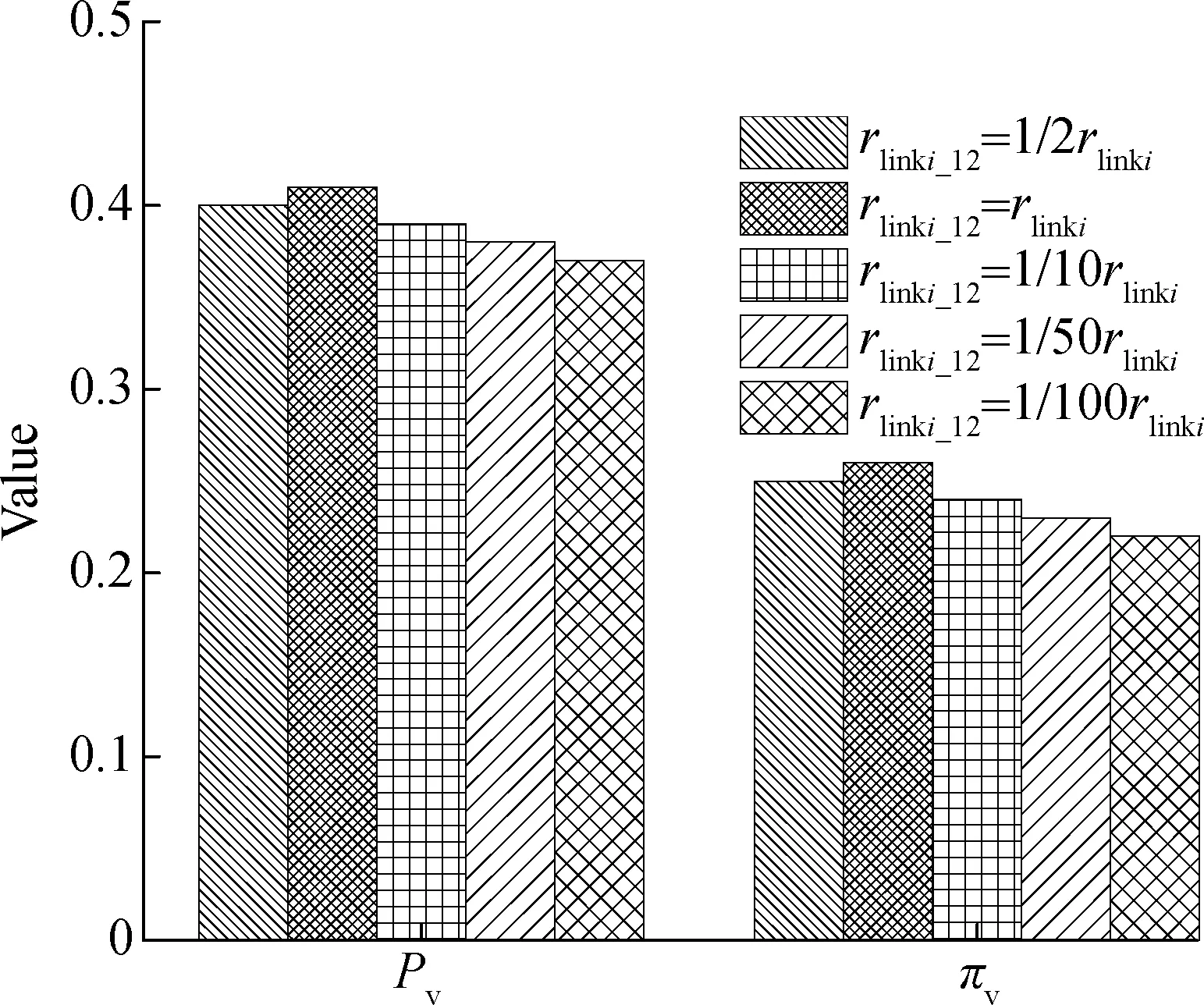
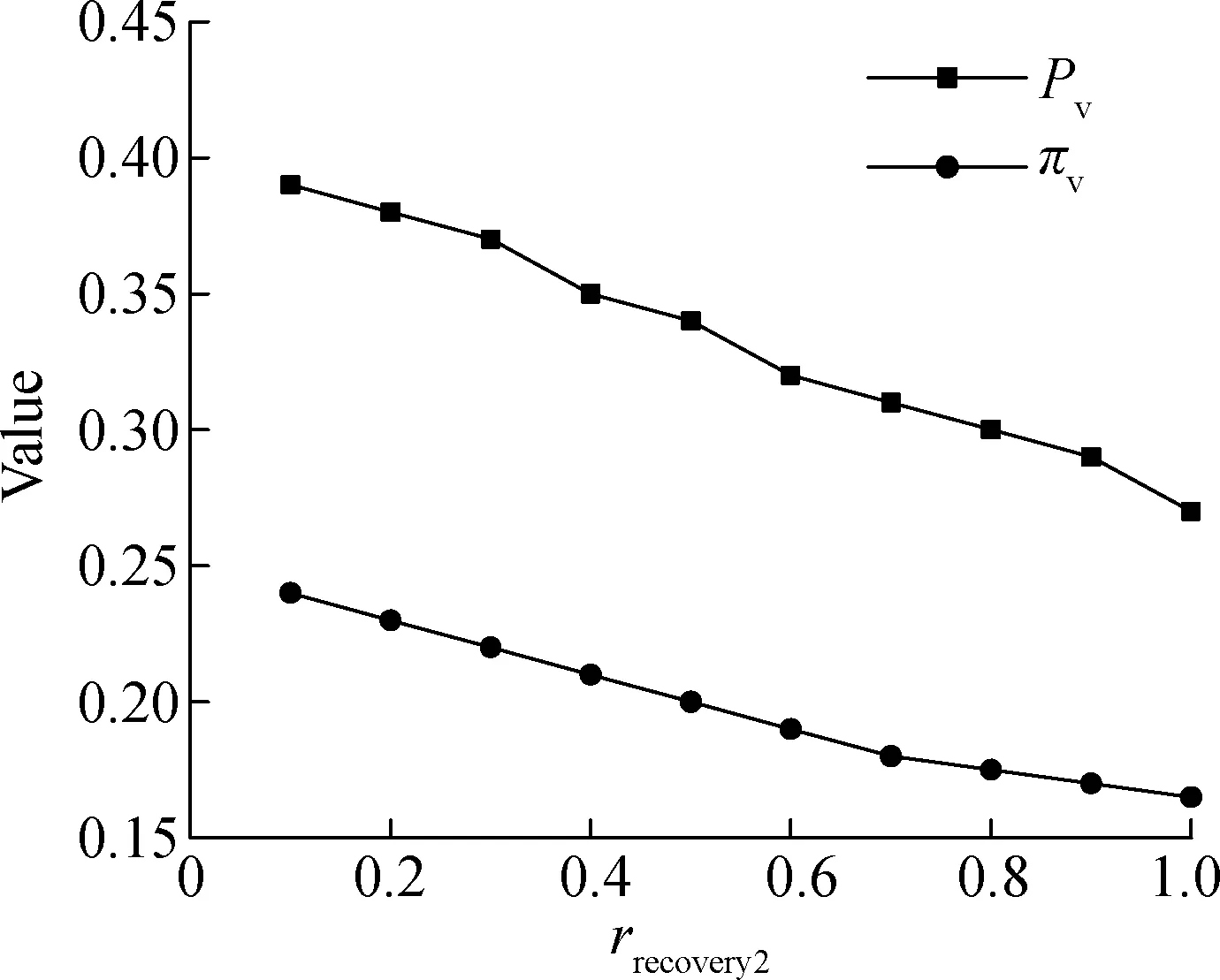
Approximate steady-state probability is the ratio of the number of units to that of components, after the model reaches a certain stable state.HypothesisX={x1,x2,…,xn},xiis the number of components in the system,Ntotalis the number of components.For any positive integeri(0

(4)

Kinetic law vectorVKLis composed of the universal set of reaction ratefk, and

(5)

whereNreactionirepresents the number of reactants.As previously mentioned,Xis the number of components and it satisfies the ordinary differential equation:

(6)

Due to the length of the paper, we will not elaborate more than is needed.Refs.[12-13] introduced the solution and derivation process of Bio-PEPA in detail.Ref.[14]introduced Bio-PEPA Eclipse plug-in syntax and modeling terminology.

2　Evolution Model of Survivability Situation

The survivability of critical cloud services in the cloud computing system is inevitably affected by the propagation of the virus.We first classify the survivability of key cloud services, and then study the impact of virus propagation in intra-domain or inter-domain.Finally, we obtain the evolution model of survivability.

2.1　Classification of survivability situation

Referring to the model of SAIR and SEIRS virus propagation, and the diffusion model in the distributed virtual system of vulnerability, the survivability of key cloud services is abstracted into 6 states: The susceptible stateS, the latent stateLe, the latent stateLc, the infection stateI, the recovery stateRand the immune stateA.By default, the latent virus is not activated or executed, so it is not infectious and can be obviously distinguished from the virus in the infected state.The specific states are as follows:

1)Srepresents that the nodes are not infected with the virus, but they have the possibility of infection.

2)Lerepresents that the nodes contain the latent virus and have been detected.

3)Lcrepresents that the nodes contain the latent virus but have not been found.

4)Irepresents that the nodes are infected with the virus and the virus has performed its part or all of predefined functions.

5)Rrepresents that the nodes are infected, but the virus has been cleared.The nodes may be transformed intoSorA.

6)Arepresents that the nodes are infected and the virus has been cleared, but the nodes have immune function to the virus or similar virus.

The state set of all nodes isW={S,Le,Lc,I,R,A}, and the virus in the latent state and the active state forms the state set of virus asLset={Le,Lc,I}.In order to further facilitate the description, we define the nodes in the stateZ∈Was componentZ.

2.2　Intra-domain propagation rules

Compared with inter-domains, viruses are more likely to be propagated in intra-domains, and therefore, we first consider the simplest case, which is the impact of viruses propagation in intra-domains.Intra-domain propagation rules of virus are as follows:

〈Propagation1〉:

1)〈link1〉S+I→2I:The componentIspreads the virus to componentSthrough the connection, and the virus is active.

2)〈link2〉S+I→Le+I: The componentIspreads the virus to the componentSthough the connection.Now the virus is in the latent state and has been found.

3)〈link3〉S+I→Lc+I: The componentIspreads the virus to the componentSthough the connection.Now the virus is in the latent state and has not been found.

4)〈activation1〉Le→I: The latent virus in the componentLeis activated.

5)〈activation2〉Lc→I: The latent virus in the componentLcis activated.

6)〈recovery1〉Le→R: The latent virus in the componentLeis cleared.

7)〈recovery2〉I→R: The latent virus in the componentIis cleared.

8)〈memory〉R→A: ComponentRis transformed into componentAby the memory function after virus clearance.

9)〈insecure1〉A→S: ComponentAis transformed into componentS.

10)〈insecure2〉A→Le: ComponentAis transformed into componentLe.

The virus propagation set is Propagation1={link1, link2, link3,activation1,activation2,recovery1,recovery2,memory, insecure1, insecure2}.The rate of change for each reaction (propagation rule)is recorded asrα, whereα∈Propagation1.Assuming that the number and type of components are fixed within a certain period of time, recording the total number of components asN, the number of componentsS,Le,Lc,I,R,Aasns,ne,nc,ni,nr,na.The reaction ratefkof each reaction satisfies

flink1=rlink1nsni,flink2=rlink2nsne,flink3=rlink3nsnc

factivation1=ractivation1neni,factivation2=ractivation2ncni

frecovery1=rrecovery1nenr,frecovery2=rrecovery2ninr

fmemory=rmemorynanr,finsecure1=rinsecure1nsna

finsecure2=rinsecure2nena

2.3　Inter-domain propagation rules

Assuming that the system is divided intonservice domains, let the domain set beK={location1, location2, …, locationn}, |K|=n, locationi, locationj∈K, locationi≠ locationj, which represent different service domains.The inter-domain propagation rules of virus are as follows:

〈Propagation2〉:

11)〈link1ij〉S@locationi+I@locationj→I@locationi+I@locationj: The componentIin service domain locationjpropagates the virus to the componentSin service domain locationiby connecting and the virus is activated.

12)〈link2ij〉S@locationi+I@locationj→Le@locationi+I@locationj: The componentIin service domain locationjpropagates the virus to the componentSin service domain locationiby connecting, and then the virus is inactivated, and it can be recognized by the system.

13)〈link3ij〉S@locationi+I@locationj→Lc@locationi+I@locationj: The componentIin service domain locationjpropagates the virus to the componentSin service domain locationiby connecting, and then the virus is inactivated, but it cannot be recognized by the system.

The rate of virus transition between locationiand locationjisrlink1-ij,rlink2-ijandrlink3-ij.The number of componentsSin locationiisnS@location-i.The number of componentsIin locationjisnI@location-j.The reaction rate offkfulfils the following rules:

flink1-ij=rlink1-ijnS@location-inI@location-j

flink2-ij=rlink2-ijnS@location-inI@location-j

flink3-ij=rlink3-ijnS@location-inI@location-j

Especially, if there is no virus propagation relationship between two service domains,rlink1-ij=rlink2-ij=rlink3-ij=0.

2.4　Formal description of Bio-PEPA model

The impact of virus propagation on the survivability of critical cloud services can be represented by the state transition of cloud service nodes.The SLIRAS model is shown in Fig.1.

Fig.1　SLIRAS model

Based on the SLIRAS model, the survivability evolution process of critical cloud service can be formally described by Bio-PEPA as follows:

S@locationi+(link3i,1)↓S@locationi+(insecure1i,1)↑

(link2i,(1,1))⊙I@locationi+(link3i,(1,1))

⊙I@locationi+(activation1i,1)↑I@locationi

+(activation2i,1)↑I@locationi+(recovery2i,1)↓

(activation1i,1)↓

Le@locationi+(recovery1i,1)↓Le@locationi+

(insecure2i,1)↑

(activation2i,1)↓

R@location+(memoryi,1)↓R@locationi

(insecure1i,1)↓A@locationi+(insecure2i,1)↓A@locationi

If there is no virus propagation between two service domains in the model, the corresponding transition rate is zero.Based on this model, we can analyze the impact of virus diffusion on the survivability of critical cloud services.

3　Simulation Analysis

Since the model contains many parameters, these parameters have a certain influence on the stability and rationality of the model.Therefore, the section will select some quantitative indicators, and briefly analyze the influence of virus propagation in intra-domains and inter-domains on the viability of critical cloud services, then compare them with the simulation test results.

3.1　Survivability assessment index

The section refers to the existing research results in the field of survivability situation assessment[15-16].Two indicators are proposed to assess the survivability situation of key cloud services: peak service quality indexPvand steady-state service quality indexπv.Letp∈Wrepresent the type of component, location represents the service domain.

Definition1(peak service quality indexPv)The index is the maximum ratio of the number of components in theLsetcollection to the number of all components in the service domain, at the time 0

(7)

wherenp@locationis the number of componentsPin the service domain location;Ntotalis the number of all components in the domain.

Definition2(steady-state service quality indexπv)The index is the sum of approximate steady state probabilities of various types of components inLsetcollection when the number of viruses in the service domain reaches a certain amount, in other words, it will no longer increase or decrease, and achieve a certain steady state:

(8)

whereπp@locationis the approximate steady-state probability of componentP.

Pvmainly measures the maximum range of virus spread in the system, whileπvcharacterizes the long-term potential impact of viruses on the system survivability[17].Next, we will analyze the impact on the survivability of key cloud services on the basis of the above two indices from the scope and trend of virus propagation.

3.2　Example selection

In a cloud computing system, survivability may be changed by virus propagation in a service domain or any two service domains.In order to highlight the core of the problem, reduce the complexity caused by the interference of other uncertainties and the differences between different service domains, we only select one of the simplest examples, as shown in Fig.2.

Fig.2　A simple example of survivability evolution

Let locationAand locationBrepresent service domains that contain several critical cloud services, respectively.The initial state of locationAcontains all kinds of components, and all components in locationBare susceptible to infection at the initial time.Virus diffusion may be present in the internal components of locationA; meanwhile, locationApropagates the virus to locationBthrough the connection.The example also includes survivability situation change caused by virus propagation in intra-domains or inter-domains.

Assuming that there areNnodes, the probability that a node which has been infected by the virus propagates the virus to another node is 1/N, that isrlink1=1/N.At the same time, due to the existence of latent viruses in nodeLeandLc, the probability of the two nodes being infected by the virus will be very high, that isrlink2=rlink3=10×1/N.The virus propagation probability of inter-domains may be smaller than that in intra-domains.We assume that the virus propagation rate of inter-domains is 1/10 that of intra-domains.In order to reduce the contrast between different service domains, highlight the difference between intra-domain diffusion and inter-domain diffusion, assume that the rate of virus propagation in locationAand locationBare the same.The parameters are shown in Tab.2.

Tab.2　The values of each parameter in the model

This paper uses the Bio-PEPA Workbench and the Bio-PEPA Eclipse plug-in to solve the model.The test environment is Windows 7, 64 bit processor, dual-core CPU, 2.4 GHz and 8 GB RAM.

It needs to be explained here that because our model adopts a formal description method, it is suitable for any given system or instance, so that the selection of instances is not the only one.

3.3　Simulation experiments

In order to test whether the proposed model is reasonable, we used the stochastic algorithm to simulate the real system and compare it with the ODEs simulation.Assuming that the number of all components in the two service domains is 200, and the initial values ofNs,Ne,Nc,Ni,Nr,Naare, respectively, (50, 10, 10, 10, 10, 10)and (100, 0, 0, 0, 0, 0).The Gillespie random algorithm[18]was used to select 10 000 groups of random data, and the error is set to be 1×10-5.The final comparison maps are shown in Fig.3 and Fig.4.

Fig.3　The comparison of stochastic simulation and ODEs simulation in locationA

As shown in Fig.3, at the beginning, there are some infection state nodes in locationA, and many nodes are susceptible to being infected.Virus propagation in intra-domains will first occur, and therefore, the number of components inLsetgenerally rises and fluctuates greatly.Later, due to the increase of memory state nodes and incomplete matching, latent state nodesLealso increase relatively.However, they are much faster to repair than susceptible state nodes.Finally, the recovery state nodes and the latent state nodesLefluctuate within a certain range, when infection state nodes decrease and approach 0; other components gradually show a steady trend.

In Fig.4, the initial state of locationBis susceptible to being infected and there are no infection state nodes.After being affected by the virus propagation in locationA, the susceptible state nodes in locationBwill rapidly decrease and will be transformed into latent state nodesLcand infected state nodes.In the process of repairing infected state nodes, memory state nodes will increase slowly.Meanwhile, the number of components inLsetrises and gradually decreases after reaching their peak value.Finally, all components will achieve a relatively stable state.

The comparisons of the two graphs show that the initial conditions of the two service domains are different, and the evolution process of the survivability state and the final results are also different.In locationA,Pv=0.37,πv=0.22; in locationB,Pv=0.39,πv=0.24.As a result, compared with locationA, locationBshows that the range of viruses propagation is wider and the impact time on service domains is longer.

3.4　Model analysis

3.4.1The effect of inter-domain virus propagation

One of the main factors that affect survivability is the virus propagation within service domains.In this paper, the virus transmission rate of inter-domains is mainly controlled byrlink1-12,rlink2-12andrlink3-12.Among them,rlinki-12containsrlink1-12,rlink2-12andrlink3-12.In order to analyze the influence of virus propagation on survivability, we usePvandπvas two indices, and consider the scope and trend of the virus propagation under a survivability situation for the whole cloud computing system.

Fig.5 shows the changes in the number of componentsLsetin locationB, when the connection raterlink1-12,rlink2-12andrlink3-12are expanded 5 times, 10 times and reduced 5 times, 10 times, respectively.As we can see from the figure, with the increase ofrlinki-12, the number of components inLsetgrows gradually, and the peak time is shortened and the peak value becomes larger.Whenrlinki-12is reduced, the number of components inLsetdecreases gradually, and the peak time increases, but the peak value decreases relatively.

According to the data in Fig.5, using Eqs.(7)and (8), we obtain the values ofPvandπvwhenrlinki-12undergoes different changes, respectively, as shown in Fig.6.

As can be seen from Fig.6, with the increase ofrlinki-12, the corresponding values ofPvare 0.40, 0.41, 0.39, 0.38, and 0.37, respectively.It means that the effect of the virus spreads with the increase of the inter-domain propagation rate.In the same way, the corresponding values ofπvare 0.25, 0.26, 0.24, 0.23, 0.22, respectively, which implies that the virus has a longer period impact on the system.This phenomenon is mainly due to the increased probability of virus propagation and the shorter propagation time.However, the overall recovery ability of the system remains unchanged, and the number of infected status nodes is increased, that is, it causes a longer recovery time of the system.

Fig.6　The effect of inter-domain propagation rate

3.4.2The effect of recovery ability

In the model, the recovery ability can make the critical services of the infected state nodes return back to normal, and it can reduce the proportion of infected nodes effectively, which is of great benefit to enhancing the survivability of the system.Next, we takePvandπvto analyze the influence of the recovery ability on survivability through the change betweenrrecovery1andrrecovery2in [0.1, 1.0].

As we can see from Fig.7 and Fig.8, with the increase ofrrecovery2,Pvandπvshow a decreasing trend, but the effect ofrrecovery1onPvandπvis not as obvious asrrecovery2.With the increase ofrrecovery1, the values ofPvandπvfluctuate within a certain range.Although there is a gradual decline in the trend, the magnitude is much smaller.This is mainly because componentsSandLcwill eventually be transformed into componentI, and componentLemay also be converted to componentI.Compared with the transformation of componentLeinto componentR, the probability of componentIto be transformed into componentRis much greater.Therefore, by enhancing the repair ability, componentIcan suppress the virus propagation more effectively.

Fig.7　The effect of rrecovery1

Fig.8　The effect of rrecovery2

3.4.3The effect of memory ability

Memory ability is a very important part of the proposed model.Due to the immune memory function and incomplete matching, the component of the recovery state can be transformed into the component of the immune state, and the possibility of reinfection is reduced.Even if infected again, it can be recovered in a relatively short time.

It can be seen from Fig.9 that the values ofPvandπvshow a linear decline trend with the improvement of memory ability, especiallyπv, and thatPvis relatively flat.The main reason is that when the memory ability of the system is enhanced, the recovery state nodes will be transformed into immune state nodes faster.As the number of nodes in the immune state increases, those nodes have a better resistance to the subsequent virus attacks.Moreover, the recovery ability of the system will be relatively enhanced, which will exert a certain inhibition effect on the virus propagation.

Fig.9　The effect of memory ability

4　Conclusions

1)Reducing the propagation rate of inter-domains can effectively control virus propagation in inter-domains, and can delay the decline trend of the system survivability.

2)Strengthening the recovery ability of a system can make the system return back to normal work as soon as possible.

3)Enhancing the memory ability of a system can greatly improve the system survivability.

In the future, we plan to study the classification of each typical virus propagation, virus variation due to the changes in the external environment, and the survival resistance mechanism within a system and so on.The model may be adjusted according to the real situation, and the impact of the other parameters in the model will also be further analyzed.

[1]Westmark V R.A definition for information system survivability [C]//Proceedingsofthe37thAnnualHawaiiInternationalConferenceonSystemScience.Washington, DC, USA: IEEE Computer Society, 2004: 2086-2096.DOI:10.1109/HICSS.2004.1265710.

[2]Mell P, Grance T.The NIST definition of cloud computing[J].CommunicationsoftheACM, 2011,53(6): 50-50.DOI: 10.6028/NIST.SP.800-145.

[3]Chang X L, Zhang Z J, Li X D, et al.Model-based survivability analysis of a virtualized system[C]//IEEE41stConferenceonLocalComputerNetworks(LCN).Dubai, United Arab Emirates, 2016: 611-614.DOI:10.1109/LCN.2016.104.

[4]Jin Y L, Zhou X Q, Bai Z S, et al.Survivability-aware topology evolution model with link and node deletion in wireless sensor networks[J].InternationalJournalofDistributedSensorNetworks, 2014,10(4): 278629.DOI:10.1155/2014/278629.

[5]Zhou J A, Miao H K, Kai J Y, et al.Survivability prediction of web system based on log statistics[C]//IEEEACIS16thInternationalConferenceonSoftwareEngineering,ArtificialIntelligence,NetworkingandParallel/DistributedComputing(SNPD).Takamatsu, Japan, 2015: 15359578.DOI:10.1109/SNPD.2015.7176170.

[6]Alobaidi I A, Sarvestani S S, Hurson A R.Survivability analysis and recovery support for smart grids[C]// 2016ResilienceWeek(RWS).Chicago, IL, USA, 2016:33-39.DOI:10.1109/rweek.2016.7573303.

[7]Moldovan R D, Todoran E N.Immune system modeling and analysis using Bio-PEPA[C]//IEEEInternationalConferenceonIntelligentComputerCommunicationandProcessing.Cluj-Napoca, Romania, 2015: 475-482.DOI:10.1109/iccp.2015.7312706.

[8]Tan Y, Zhang P.Immune based computer virus detection approaches[J].CAAITransactionsonIntelligentSystem, 2013,8(1): 80-94.DOI:10.3969/j.issn.1673-4785.201209059.

[9]Piqueira J R C, de Vasconcelos A A, Gabriel C E C J, et al.Dynamic models for computer viruses[J].Computers&Security, 2008,27(7): 355-359.DOI:10.1016/j.cose.2008.07.006.

[10]Li J, Yang Y, Zhou Y.Global stability of an epidemic model with latent stage and vaccination[J].NonlinearAnalysis:RealWorldApplications, 2011,12(4): 2163-2173.DOI:10.1016/j.nonrwa.2010.12.030.

[11]Lü H W, Wang H Q, Lin J Y, et al.A vulnerability propagation model of distributed virtualized systems based on Bio-PEPA[J].ChineseJournalofComputers, 2016,39(2): 391-404.DOI:10.11897/SP.J.1016.2016.00391.(in Chinese)

[12]Ciocchetta F, Hillston J.Bio-PEPA: A framework for the modelling and analysis of biological systems[J].TheoreticalComputerScience, 2009,410(33): 3065-3084.DOI:10.1016/j.tcs.2009.02.037.

[13]Galpin V.Hybrid semantics for Bio-PEPA[J].InformationandComputation, 2014,236: 122-145.DOI:10.1016/j.ic.2014.01.016.

[14]Duguid A.An overview of the Bio-PEPA eclipse plug-in[C]//EighthWorkshoponProcessAlgebraandStochasticallyTimeActivities.Edinburgh, UK, 2009: 121-132.

[15]Zhao J, Zhou Y, Shuo L.A situation awareness model of system survivability based on variable fuzzy set[J].IndonesianJournalofElectricalEngineeringandComputerScience, 2012,10(8): 2239-2246.DOI:10.11591/telkomnika.v10i8.1691.

[16]Chen T P, Cui W Y, Meng X R, et al.A method of IP network survivability evaluation method under performance monitoring[J].JournalofBeijingUniversityofPostsandTelecommunications, 2015,38(6):20-23.DOI:10.13190/j.jbupt.2015.06.005.(in Chinese)

[17]Van Mieghem P, Omic J, Kooij R.Virus spread in networks[J].IEEE/ACMTransactionsonNetworking, 2009,17(1): 1-14.DOI:10.1109/tnet.2008.925623.

[18]Gillespie D T.Stochastic simulation of chemical kinetics[J].AnnualReviewofPhysicalChemistry, 2007,58(1): 35-55.DOI:10.1146/annurev.physchem.58.032806.104637.